Albert Meads Fisher

Department of Mathematics, University of São Paulo

e-mail: afisher-at-ime.usp.br

  • Institute of Mathematics and Statistics
  • University of São Paulo
  • Google Scholar Citations
  • USP Digital

    • Areas of Interest

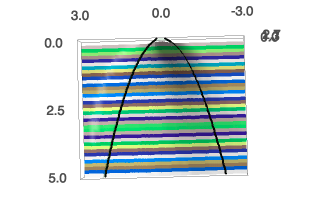
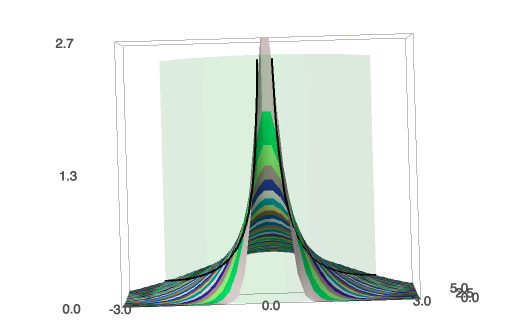
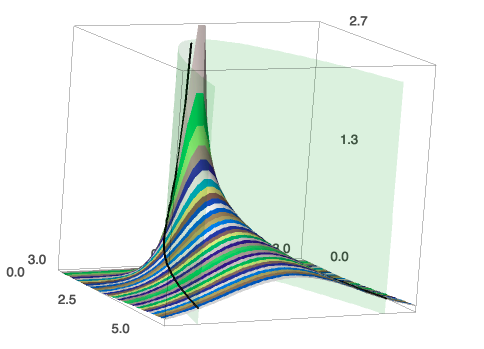
    This shows the fundamental solution of one-dimensional heat equation. Black curve marks constant variance. Click for rotatable 3d image!!

    Some papers

  • Uniform distribution mod 1 for sequences of ergodic sums and continued fractions, Preprint, July 27, 2023, 9 pp. (Albert M. Fisher, Xuan Zhang) arXiv

  • Asymptotic self-similarity and order-two ergodic theorems for renewal flows, Journal d'Analyse Mathématique, September 2015, Volume 127, Issue 1, pp 1-45 (with Marina Talet)pdf,

  • Distribution of approximants and geodesic flows, Ergodic Theory and Dynamical Systems, Volume 34, Issue 06, December 2014, pp 1832-1848 doi:10.1017/etds.2013.23. (with Tom Schmidt) pdf,

  • Dynamical attraction to stable processes, Ann. Inst. H. Poincaré Probab. Statist. Volume 48, Number 2, 2012, pp 551-578 (with Marina Talet) pdf,

  • The self-similar dynamics of renewal processes, Electron. J. Probab. 16, Article 31, May 10, 2011, pp 929-961 (with Marina Talet) pdf,

  • Minimality and unique ergodicity for adic transformations, Journal d'Analyse Mathematique, 109(1): October 2009, pp 1-31 (with Sebastien Ferenczi and Marina Talet) pdf,

  • Nonstationary mixing and the unique ergodicity of adic transformations, Stochastics and Dynamics, Volume 9 (3), 2009, pp 335-391 pdf,

  • Anosov families, renormalization and nonstationary subshifts, Ergodic Theory and Dynamical Systems { 25}, 2005, pp. 661-709 (with Pierre Arnoux) pdf, (preprint version containing all final corrections for ETDS; initial preprint Univ. de Marseilles, February 2003),

  • Small-scale structure via flows, Expository article: Conference Proceedings, Fractal Geometry and Stochastics III, Friedrichroda, Germany, March 17-22, 2003, pp 59-78 pdf, preprint version: pdf,

  • The scenery flow for hyperbolic Julia sets, Proceedings London Math. Soc. (3) 85, 2002, pp 467-492 (with Tim Bedford and Mariusz Urbanski) pdf,

  • Exact bounds for the polynomial decay of correlation, 1/f noise and the {CLT} for the equilibrium state of a non-Holder potential, Nonlinearity, 2001, vol 14, pp 1071-1104 (with Artur Lopes) pdf,

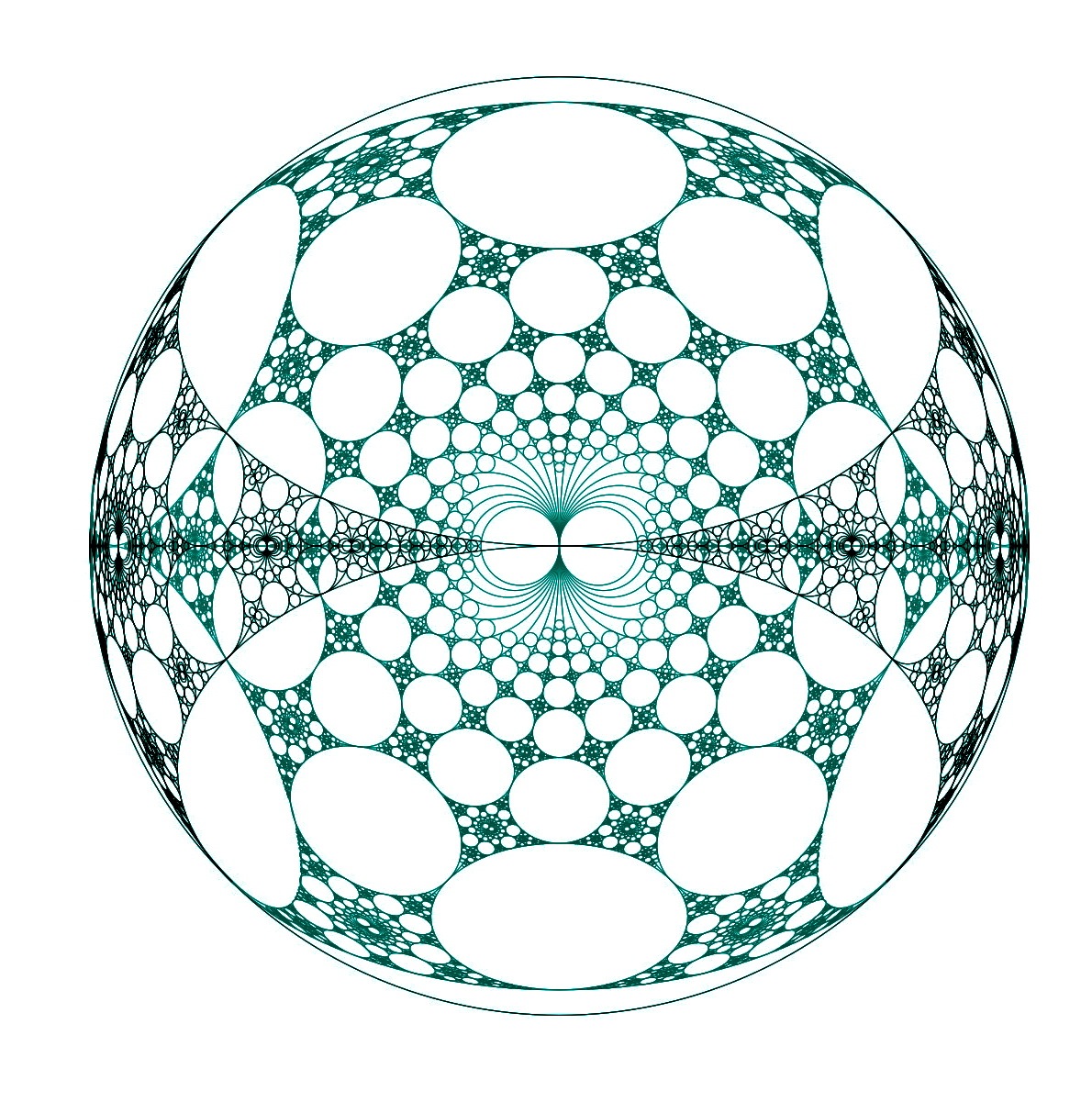
  • The scenery flow for geometric structures on the torus: The linear setting, Chinese Annals of Mathematics 22b, no. 4, 2000, pp 427-470 (with Pierre Arnoux) pdf; (figures are better here than in published version) ,

  • On invariant line fields, Bulletin London Math. Soc. 32, 2000, pp 555-570 (with Mariusz Urbanski) pdf ,

  • A Poisson formula for harmonic projections, Annales de l'Institut H. Poincaré, Probabilités et Statistiques 2 (34) 1998, pp 209-216 (with V. Kaimanovich), pdf ,



  • Ratio geometry, rigidity and the scenery process for hyperbolic Cantor sets, Erg. Th. and Dyn. Sys. 17, 1997, pp 531-564 (with Tim Bedford), pdf,

  • Analogues of the Lebesgue density theorem for fractal sets of reals and integers, Proc. London Math. Soc. 64, 1992, pp 95-124, pdf,

  • Second order ergodic theorems for ergodic transformations of infinite measure spaces, Proc. AMS 114 (1), 1992, pp 115-128 (with J. Aaronson and M. Denker), pdf,

  • Integer Cantor sets and an order-two ergodic theorem, Ergod. Th. and Dynam. Sys. 13, 1992, pp 45-64, pdf,

  • Convex-invariant means and a pathwise central limit theorem, Adv. Math. 63, 1987, pp 213-246. pdf.

    • Expository notes

  • Small-scale structure and randomness: the scenery flow in dynamics, geometry and probability (text updated December 2005, references updated March 2009). 34 pp. pdf, (English version of thesis for livre-docência, July 2003, USP; this is similar to the French or German Habilitation).

  • Survey of research. 10 pp. gzipped ps, (introduction to research and to the updated version of the livre-docência thesis, December 2005).

    • Links to some videotaped lectures:

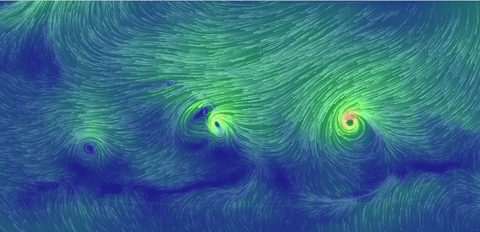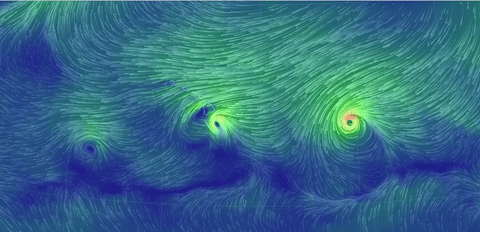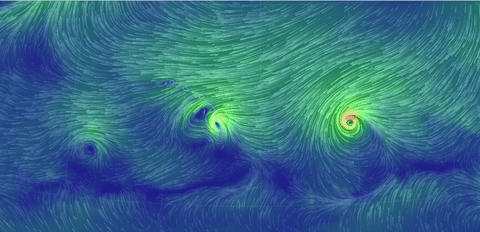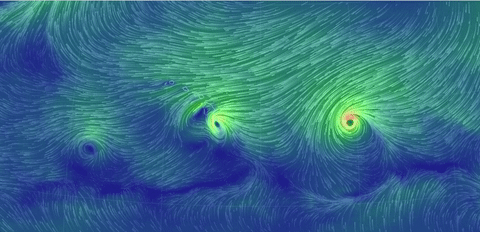
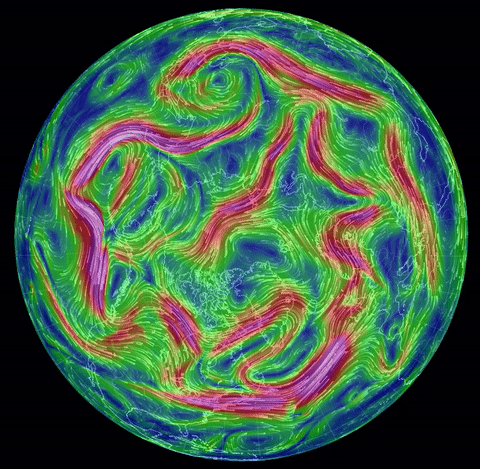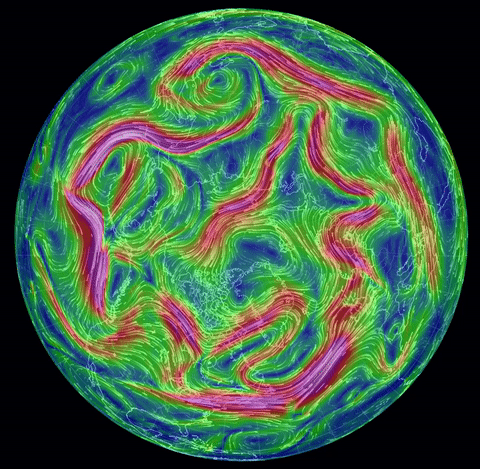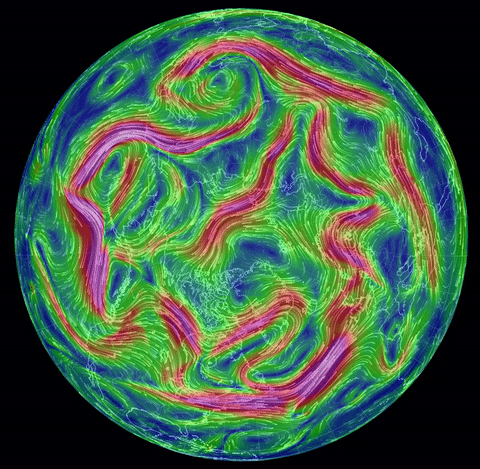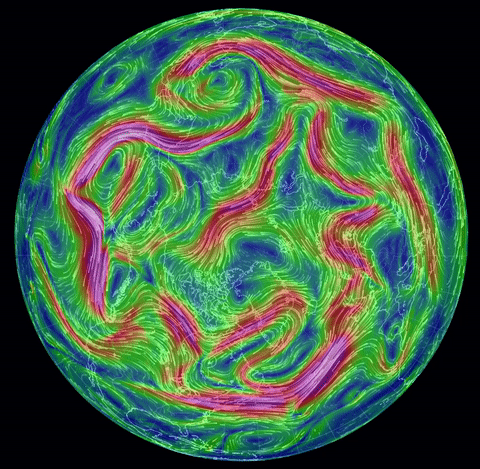
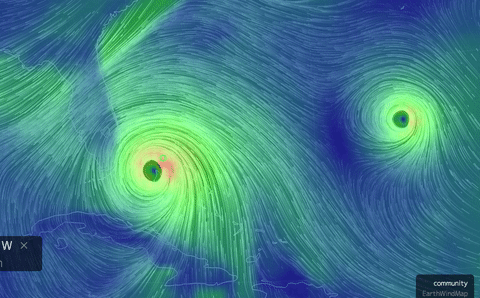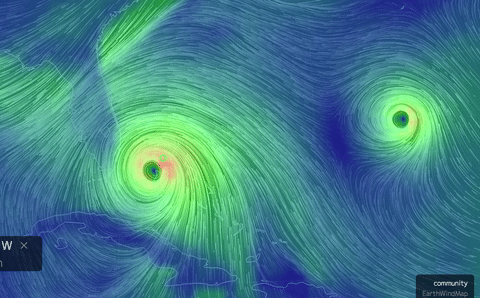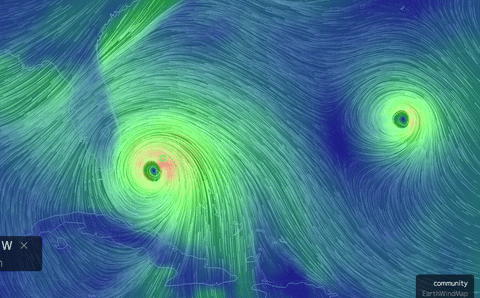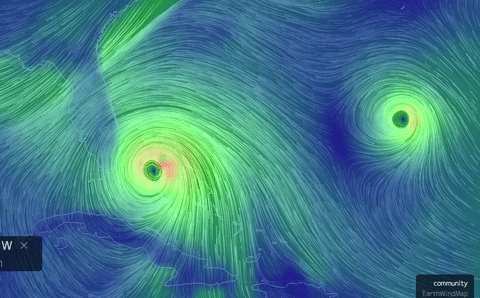
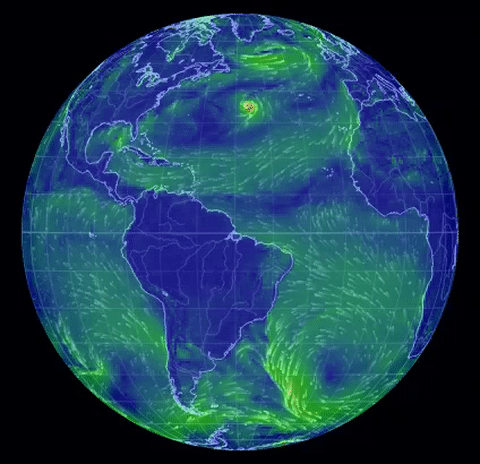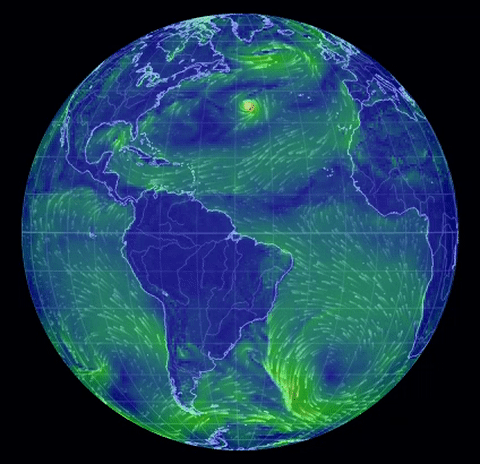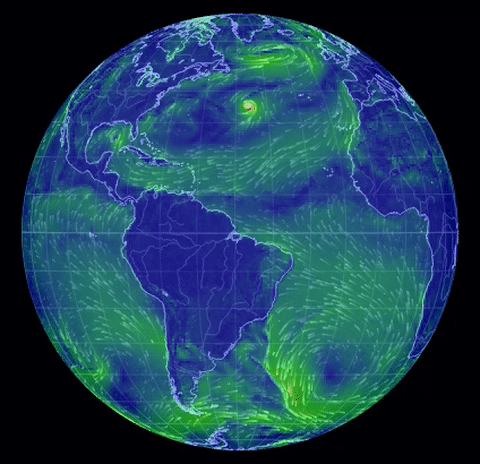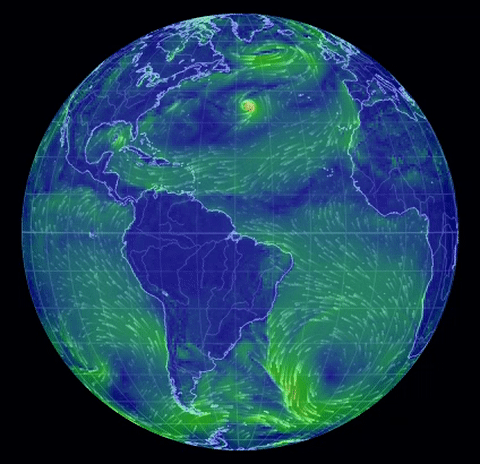
    The real-world (!) nonstationary flows depicted here come from the spectacular site nullschool.net Earth Wind Map, (click on "earth" there for an explanation). The gif near the top shows surface winds on August 31, 2016. Others show two hurricanes nearing Hawaii, and the jet stream (North Pole view), same date, and twin hurricanes approaching Florida, Oct. 6. The interface is Google-Earth like and the information is almost real-time, being updated every three hours. One can view wind speeds at different altitudes, also currents and wave motion, also concentration of pollutants and ocean surface temperature anomalies. And if you are lucky you might see a real-world Reeb Foliation ! Here is one from June 03, 2017.

    Ensinamento, 2o semestre de 2024:

  • MAT 2464, BE, Calculo II

    • Dynamics lecture notes:

  • Lecture Notes on Dynamical Systems and Ergodic Theory preliminary version, August 8, 2023; 483 pp.
    • (pdf)

    Lecture notes on Vector Calculus (Calc 2,3):

  • Lecture Notes on Vector Calculus, Vector Fields and Differential Equations, May 16, 2024, 130 pp.
    • (pdf)

    Some useful math links

  • AMS page
  • MathSciNet

    • Math links: institutions

  • Institute of Mathematics and Statistics, University of São Paulo
  • IMS, Stony Brook University
  • Dynamics page, IMS, Stony Brook University
  • IML, Luminy, Marseilles
  • CIRM, Luminy, Marseilles
  • IHES, Paris
  • IMPA, Rio de Janeiro
  • MSRI, Berkeley
  • ESI (Erwin Schrödinger Institute), Vienna