Algoritmos para Grafos  |  Índice

Algoritmo de Kosaraju para componentes fortes

Em muitas aplicações é possível (e muito proveitoso) processar cada componente forte de um grafo em separado. Por isso, a habilidade de encontrar as componentes fortes rapidamente é muito útil.

S. Rao Kosaraju e M. Sharir descobriram (em 1978 e 1981 respectivamente) um algoritmo muito eficiente para calcular as componentes fortes de um grafo.  Seria justo usar a expressão algoritmo de Kosaraju-Sharir para designar o algoritmo, mas vamos simplificar e dizer apenas algoritmo de Kosaraju.

O algoritmo

É tentador imaginar que cada etapa de uma busca em profundidade revela uma componente forte do grafo.  Infelizmente, isso só é verdade se o vértice inicial de cada nova etapa for escolhido de uma maneira especial. Para fazer essa escolha especial, o algoritmo de Kosaraju começa por colocar os vértices numa certa ordem, determinada por uma busca em profundidade preliminar. O algoritmo pode ser descrito assim:

1. Ao receber um grafo G, inverta a direção de cada arco, obtendo assim o grafo reverso G^R.  Em seguida, faça uma busca DFS em G^R para calcular uma permutação em pós-ordem, digamos  v₀ v₁ v₂ … v_n−1, dos vértices de G^R.
2. Faça uma busca DFS em G examinando os vértices na ordem  v_n−1 … v₂ v₁ v₀  para iniciar cada nova etapa da busca.  Em cada etapa da busca, o conjunto dos vértices descobertos induz uma componente forte de G.

O passo 1 é conhecido como primeira fase do algoritmo; o passo 2 constitui a segunda fase.  A segunda fase é semelhante ao algoritmo de eliminação iterada de sorvedouros, que decide se um grafo tem ciclos.

Exemplo A.  Considere o grafo G definido pelas listas de adjacência abaixo. Note que G é um dag.

0:  3 4  
1:  3  
2:  4 7  
3:  5 6 7   
4:  6    
5:      
6:    
7:  

Veja as listas de adjacência do grafo reverso G^R:

0:  
1:  
2:  
3:  0 1
4:  0 2
5:  3
6:  3 4
7:  2 3

Faça uma busca DFS em G^R. A floresta DFS consiste em oito vértices isolados. Veja a numeração dos vértices de G^R em pós-ordem:

     v   0 1 2 3 4 5 6 7
post[v]  0 1 2 3 4 5 6 7

(Essa numeração dos vértices é anti-topológica pois G^R é um dag.)  Agora faça uma busca DFS no grafo original G, tomando os vértices na ordem  7 6 5 4 3 2 1 0  ao escolher o vértice inicial de cada nova etapa.  Como G é um dag, cada etapa descobre apenas um vértice.

Exemplo B.  Seja G o grafo definido pelas listas de adjacência abaixo. (Trata-se de um dag isomorfo ao do exemplo A.)

0:  
1:  
2:  
3:  1
4:  0 1 2    
5:  0 3    
6:  3 4  
7:  4

A seguir, veja as listas de adjacência do grafo reverso G^R e uma floresta DFS em G^R (você deve imaginar que todos os arcos da figura estão dirigidos de cima para baixo).

    0      1    2 
   / \     |      
  4   5    3      
 / \              
6   7             

0:  4 5
1:  3 4
2:  4
3:  5 6 
4:  6 7
5:  
6:  
7:  

Veja a numeração dos vértices de G^R em pós-ordem:

     v   6 7 4 5 0 3 1 2
post[v]  0 1 2 3 4 5 6 7

Agora faça uma busca DFS no grafo original G, examinando os vértices na ordem  2 1 3 0 5 4 7 6  ao escolher o vértice inicial de cada nova etapa.  (Essa permutação dos vértices de G é topológica pois G é um dag.)  Cada etapa descobre apenas um vértice, como era de se esperar uma vez que G é um dag.

Exemplo C.  Seja G o grafo definido pelas listas de adjacência abaixo (o mesmo grafo do exemplo A do capítulo Algoritmo de Tarjan, mas com nomes alfabéticos para os vértices).

a:  b g  
b:  c f  
c:  b d  
d:  e    
e:  d    
f:  c    
g:  h i  
h:  d g j
i:  h    
j:       

A seguir, veja as listas de adjacência do grafo reverso G^R e uma floresta DFS de G^R (você deve imaginar que todos os arcos da figura estão dirigidos de cima para baixo).

a     b     d     j 
     /     / \      
    c     e   h     
   /         / \    
  f         g   i   

a:  
b:  a c
c:  b f
d:  c e h
e:  d
f:  b
g:  a h
h:  g i
i:  g
j:  h

Veja a numeração dos vértices de G^R em pós-ordem:

     v   a f c b e g i h d j
post[v]  0 1 2 3 4 5 6 7 8 9

 j    d     h     b    a 
     /     /     / \     
    e     g     c   f    
         /               
        i                

Agora veja uma busca DFS no grafo original G, com os vértices considerados na ordem  j d h i g e b c f a  ao escolher o início de cada nova etapa. Observe que cada árvore da floresta DFS corresponde a uma componente forte de G.

Implementação

Nossa implementação do algoritmo de Kosaraju calculará uma numeração dos vértices que identifique a componente forte a que cada vértice pertence. Essa numeração será armazenada num vetor sc[0..V-1]. (O nome do vetor é uma abreviatura de strong component.)  Portanto, sc[v] valerá k se v estiver na k-ésima componente forte.

static int cnt, pre[1000];
static int cntt, post[1000];
static vertex vv[1000];

/* Esta função atribui um rótulo sc[v]
   (os rótulos são 0,1,2,...)
   a cada vértice v do grafo G de modo que dois vértices 
   tenham o mesmo rótulo
   se e somente se os dois pertencem à mesma componente forte.
   A função devolve o número (quantidade) de
   componentes fortes de G.
   (A função implementa o algoritmo de Kosaraju.
   O código é adaptado do Programa 19.10 de Sedgewick.) */

int GRAPHstrongCompsK( Graph G, int *sc) 
{
   // fase 1:
   Graph GR = GRAPHreverse( G);
   cnt = cntt = 0;
   vertex v; 
   for (v = 0; v < GR->V; ++v) pre[v] = -1;
   for (v = 0; v < GR->V; ++v) 
      if (pre[v] == -1)
         dfsR( GR, v); 
   for (v = 0; v < GR->V; ++v) 
      vv[post[v]] = v;
   // vv[0..V-1] é permutação de GR em pós-ordem

   // fase 2:
   for (v = 0; v < G->V; ++v) sc[v] = -1;
   int k = 0;
   for (int i = G->V-1; i >= 0; --i) {
      v = vv[i];
      if (sc[v] == -1) { // nova etapa
         dfsRstrongCompsK( G, v, sc, k);
         k++;
      }
   }
   GRAPHdestroy( GR);
   return k;
}

/* Constrói o reverso do grafo G. */

Graph GRAPHreverse( Graph G) 
{
   Graph GR = GRAPHinit( G->V);
   for (vertex v = 0; v < G->V; ++v) 
      for (link a = G->adj[v]; a != NULL; a = a->next)
         GRAPHinsertArc( GR, a->w, v);
   return GR;
}

Na fase 1, o algoritmo faz uma busca DFS no grafo GR a partir do vértice v:

/* Armazena no vetor post[]
   uma numeração em pós-ordem do grafo GR.
   O vetor pre[] marca os vértices já descobertos. */

static void dfsR( Graph GR, vertex v) 
{ 
   pre[v] = cnt++; 
   for (link a = GR->adj[v]; a != NULL; a = a->next)
      if (pre[a->w] == -1) 
         dfsR( GR, a->w); 
   post[v] = cntt++;
}

No fim da fase 1, a numeração post[] é transformada na correspondente permutação vv[] dos vértices.  A fase 2 faz uma busca DFS no grafo G. Ao passar de uma etapa da busca para outra, os vértices são considerados na ordem inversa de vv[].

/* Atribui o rótulo k
   a todo vértice w
   ao alcance de v
   que ainda não foi rotulado.
   Os rótulos são armazenados no vetor sc[]. */

static void dfsRstrongCompsK( Graph G, vertex v, int *sc, int k) 
{ 
   sc[v] = k;
   for (link a = G->adj[v]; a != NULL; a = a->next)
      if (sc[a->w] == -1) 
         dfsRstrongCompsK( G, a->w, sc, k);
}

Exemplo D.  Considere a aplicação da função GRAPHstrongCompsK() ao grafo G definido pelas listas de adjacência abaixo (o grafo é o mesmo do exemplo B do capítulo Algoritmo de Tarjan).

0:  1
1:  2
2:  3 5
3:  4
4:  3
5:  1 3

A seguir, veja as listas de adjacência do grafo reverso GR e uma floresta DFS de GR.  A correspondente permutação dos vértices de GR em pós-ordem é  0 2 5 1 4 3.

0     1     3 
     /     /  
    5     4   
   /          
  2           

0:  
1:  0 5
2:  1
3:  2 4 5
4:  3
5:  2

   3     1    0 
  /     /       
 4     2        
      /         
     5          

Agora veja o resultado de uma busca DFS no grafo original G, com os vértices examinados na ordem  3 4 1 5 2 0  ao escolher o vértice inicial de cada nova etapa. Cada árvore dessa floresta DFS corresponde a uma componente forte de G.

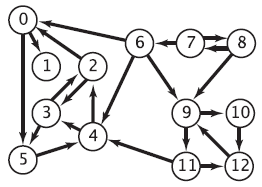
Exemplo E.  Considere a aplicação da função GRAPHstrongCompsK() ao grafo G da figura à direita.  A figura seguinte mostra o grafo reverso GR. Faça uma busca DFS em GR tomando os vértices em ordem em crescente de nomes (poderia ter tomado qualquer outra ordem).  Isso produz o seguinte vetor post[]:

     v    0  1  2  3  4  5  6  7  8  9 10 11 12
post[v]  11 12 10  9  8  0  3  2  1  6  4  7  5

e portanto a seguinte permutação dos vértices em pós-ordem:

    5 8 7 6 10 12 9 11 4 3 2 0 1

A fase 1 do algoritmo está concluída. Agora faça uma busca DFS no grafo original G tomando os vértices na ordem inversa à da permutação acima.  A primeira etapa da busca começa no vértice 1 e descobre apenas o vértice

    1

Esse vértice induz a primeira componente forte.   A segunda etapa da busca começa com o vértice 0 e descobre o conjunto de vértices

    0 5 4 2 3

que induz a segunda componente forte.   A terceira etapa começa com o vértice 11 e descobre o conjunto de vértices

   11 12 9 10

que induz a terceira componente forte.   A quarta etapa começa com o vértice 6 e descobre o vértice

    6

e nada mais. Esse vértice induz a quarta componente forte.   A quinta etapa começa com o vértice 7 e descobre os vértices

    7 8

que induzem a quinta componente forte.

Desempenho

Quanto tempo a função GRAPHstrongCompsK() consome?  Como o algoritmo consiste essencialmente em uma inversão do grafo e duas buscas em profundidade, o consumo de tempo é da ordem de V + A, sendo V o número de vértices e A o número de arcos do grafo G.  (Se A ≥ V, como acontece em muitas aplicações, podemos dizer que o consumo de tempo é proporcional a A.)

O algoritmo de Kosaraju é, portanto, linear no tamanho do grafo.

Por que o algoritmo está correto?

Não é nada óbvio que o algoritmo de Kosaraju produz o resultado que promete.  A prova da correção do algoritmo tem por base a seguinte relação entre as componentes fortes de um grafo e a permutação dos vértices do grafo em pós-ordem:

Eis um esboço da prova da propriedade: Considere a busca DFS em H que produziu a permutação v₀ v₁ … v_n−1. Suponha primeiramente que r é descoberto antes de qualquer vértice de S. Então todos os vértices de S são descobertos e morrem durante o intervalo de vida de r. Logo, r é ancestral de todos os vértices de S.  Suponha agora que r é descoberto depois de algum vértice de S. Como r não está ao alcance de nenhum dos vértices de S, todos os vértices de S são descobertos e morrem antes de r. Portanto, r é primo direito de todo vértice de S.

Prova da correção do algoritmo.  Para provar que o algoritmo de Kosaraju está correto, basta mostrar que cada etapa da fase 2 do algoritmo produz uma nova componente forte do grafo G.  É preciso lembrar que na fase 2 do algoritmo temos uma permutação em pós-ordem v₀ v₁ … v_n−1 dos vértices do grafo reverso G^R e que a fase 2 processa os vértices de G na ordem inversa dessa permutação.  Cada etapa da fase 2 consiste em uma busca DFS em G a partir do vértice não descoberto de maior índice. Digamos que esse vértice é  v_i  e seja S o conjunto de vértices da componente forte que contém v_i . Precisamos provar que a busca a partir de v_i descobre todos os vértices de S e somente esses. Eis as duas partes da prova:

1. É claro que cada vértice de S está ao alcance de v_i.  Além disso, podemos supor, a título de hipótese de indução, que nenhum vértice de S foi descoberto antes do início dessa etapa. Portanto, a busca a partir de v_i descobrirá todos os vértices de S.
2. Suponha agora, para obter uma contradição, que a busca a partir de v_i descobre algum vértice que não pertence a S. Seja v_k o primeiro tal vértice. Então algum arco do grafo vai de S a v_k.  No grafo reverso G^R, o conjunto S induz uma componente forte e existe um arco de v_k a S. Assim, se tomarmos H = G^R na Propriedade da Pós-Ordem, concluiremos que  k > i .  Mas isso é impossível, pois todos os vértices do conjunto {v_i+1 v_i+2 … v_n−1} foram descobertos antes do início da etapa corrente. Essa contradição mostra que todos os vértices descobertos a partir de v_i pertencem a S.

Provamos assim que o algoritmo de Kosaraju está correto.