Algoritmos para Grafos | Índice
A busca DFS numera os vértices de um grafo em pré-ordem. Este capítulo mostra que a busca também pode numerar os vértices em pós-ordem. A combinação das duas numerações é essencial para decidir eficientemente se um dado arco do grafo é de avanço, de retorno, ou cruzado em relação à floresta DFS. A classificação dos arcos não resolve um problema específico, mas serve de pré-processamento em algoritmos eficientes para diversos problemas.
A floresta DFS é o esqueleto do grafo
e os vetores pre[] e post[]
mostram como os demais arcos do grafo se encaixam
nesse esqueleto.
Assim, a busca DFS revela a forma, a cara
, do grafo.
Sumário:
Durante uma busca em profundidade, um vértice v morre quando a execução da encarnação dfsR(G,v) de dfsR() termina. Em outras palavras, um vértice morre depois que todos os seus vizinhos em G e todos os seus descendentes na floresta DFS forem visitados. A ordem em que os vértices morrem é conhecida como pós-ordem (= postorder).
(Se o grafo for uma árvore radicada, a permutação dos vértices em pós-ordem pode ser descrita recursivamente: para cada vizinho w da raiz, visite, em pós-ordem, a subárvore que tem raiz w; depois, visite a raiz.)
A seguinte extensão das funções GRAPHdfs() e dfsR() numera os vértices em pós-ordem. A numeração é registrada num vetor post[] indexado pelos vértices: o m-ésimo vértice a morrer recebe número m .
static int cnt, pre[1000]; static int cntt, post[1000]; static vertex pa[1000];
void GRAPHdfs( Graph G) { cnt = cntt = 0; for (vertex v = 0; v < G->V; ++v) pre[v] = -1; for (vertex v = 0; v < G->V; ++v) if (pre[v] == -1) { pa[v] = v; dfsR( G, v); } }
static void dfsR( Graph G, vertex v) { pre[v] = cnt++; for (link a = G->adj[v]; a != NULL; a = a->next) if (pre[a->w] == -1) { pa[a->w] = v; dfsR( G, a->w); } post[v] = cntt++; // numeração em pós-ordem }
A variável cnt conta as descobertas de vértices e fornece os valores de pre[]. A variável cntt conta as mortes de vértices e fornece os valores de post[].
Exemplo A. Considere a aplicação da função GRAPHdfs() ao grafo G definidos pelas seguintes listas de adjacência:
0: 4 5 1: 0 2: 3: 4: 2 3 5:
Veja o rastreamento da execução de GRAPHdfs( G):
0 dfsR(G,0)
0-4 dfsR(G,4)
4-2 dfsR(G,2)
2
4-3 dfsR(G,3)
3
4
0-5 dfsR(G,5)
5
0
1 dfsR(G,1)
1-0
1
As linhas que começam com v-w registram o momento em que a função dfsR() percorre o arco v-w. As linhas que têm um vértice v e nada mais representam o instante em que o vértice v morre. O rastreamento mostra que os vértices morrem na ordem 2 3 4 5 0 1. Essa é, então, a permutação dos vértices em pós-ordem. Portanto, o vetor post[] termina no seguinte estado:
v 2 3 4 5 0 1
post[v] 0 1 2 3 4 5
Se preferir, você pode reescrever essa tabela de modo que a primeira linha fique na ordem crescente usual:
v 0 1 2 3 4 5
post[v] 4 5 0 1 2 3
Exemplo B. Considere a aplicação da função GRAPHdfs() ao grafo G definidos pelas seguintes listas de adjacência:
0: 1 4 1: 2: 0 3 4 3: 4 5 4: 1 5 5: 1
Veja o rastreamento da execução de GRAPHdfs( G):
0 dfsR(G,0)
0-1 dfsR(G,1)
1
0-4 dfsR(G,4)
4-1
4-5 dfsR(G,5)
5-1
5
4
0
2 dfsR(G,2)
2-0
2-3 dfsR(G,3)
3-4
3-5
3
2-4
2
O rastreamento mostra que 1 5 4 0 3 2 é a permutação dos vértices em pós-ordem (veja as linhas em que aparece apenas o nome de um vértice). Segue daí o estado final do vetor post[]:
v 1 5 4 0 3 2
post[v] 0 1 2 3 4 5
Para completar o exemplo, veja o estado final dos vetores pre[] e pa[]:
w 0 1 4 5 2 3
pre[w] 0 1 2 3 4 5
pa[w] 0 0 0 4 2 2
0 2
0/3 4/5
/ \ |
1 4 3
1/0 2/2 5/4
\
5
3/1
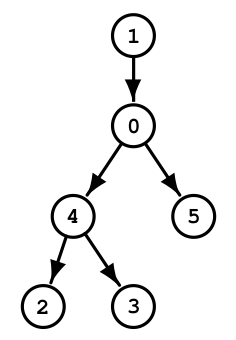
(Atenção! Os conjuntos de valores dos dois vetores são diferentes: enquanto pre[] é um vetor de números inteiros, pa[] é um vetor de vértices.) Para resumir, veja uma figura da floresta DFS com o par pre/post escrito abaixo do nome de cada vértice:
grafo-caminho0-1 1-2 2-3 3-4 4-5 5-6. Observe o vetor post[] produzido. Repita o exercício da seguinte maneira: para escolher o vértice inicial de cada nova etapa da busca, examine os vértices em alguma ordem diferente da ordem 0, 1, 2, 3, etc. usual. Qual o efeito sobre o vetor post[]?
Cada encarnação de dfsR() permanece em execução durante um certo intervalo de tempo. A encarnação dfsR(G,v) permanece em execução entre o instante em que v é descoberto e o instante em que v morre. Diremos que esse é o intervalo de vida (= lifespan) da encarnação. É claro que o início do intervalo corresponde a pre[v] e o fim do intervalo corresponde a post[v]. (Mas não faz sentido dizer que o intervalo é (pre[v],post[v]) pois as duas numerações são independentes!)
Em virtude do caráter recursivo de dfsR(),
a coleção dos intervalos de vida
de todas as encarnações de dfsR() é bem organizada
no seguinte sentido:
cada dois intervalos são disjuntos ou estão encaixados.
(Veja exercícios
no capítulo Florestas DFS.)
Em outras palavras,
se um vértice x é descoberto antes de um vértice y
então morre antes que y seja descoberto
(caso de intervalos disjuntos)
ou morre depois que y tenha morrido
(caso de intervalos encaixados).
Os exemplos a seguir mostram que é fácil observar os intervalos de vida das várias encarnações de dfsR() no rastreamento da execução de GRAPHdfs().
Exemplo C. Considere novamente o rastreamento da execução de GRAPHdfs( G) no exemplo B. Veja a indicação dos intervalos de vida das várias encarnações de dfsR();
0 dfsR(G,0) 0
0-1 dfsR(G,1) 0 1
1 0 1
0-4 dfsR(G,4) 0 4
4-1 0 4
4-5 dfsR(G,5) 0 4 5
5-1 0 4 5
5 0 4 5
4 0 4
0 0
2 dfsR(G,2) 2
2-0 2
2-3 dfsR(G,3) 2 3
3-4 2 3
3-5 2 3
3 2 3
2-4 2
2 2
Essa coleção de intervalos pode ser representada
por uma permutação dupla
dos vértices,
isto é,
uma sequência em que cada vértice aparece exatamente duas vezes.
A primeira aparição de um vértice x
corresponde ao início da execução de dfsR(G,x)
e a segunda corresponde ao fim da execução de dfsR(G,x):
0 2
/ \ |
1 4 3
\
5
0 1 1 4 5 5 4 0 2 3 3 2 ( ( ) ( ( ) ) ) ( ( ) )
Cada dois intervalos nessa permutação dupla estão encaixados (como 5 e 4, por exemplo) ou são disjuntos (como 4 e 1, por exemplo). Essa expressão de parênteses nada mais é que uma representação alternativa da floresta DFS.
Exemplo D. Aplique a função GRAPHdfs() ao grafo representado pelas seguintes listas de adjacência:
0: 2 4 1: 3 2: 7 3: 6 4: 5 7 5: 4 1 7 6: 0 2 4 7: 5 3
Veja o rastreamento da execução de GRAPHdfs(). Para tornar o exemplo mais interessante, começamos a busca pelo vértice 2 e não pelo vértice 0:
2 dfsR(G,2)
2-7 dfsR(G,7)
7-5 dfsR(G,5)
5-4 dfsR(G,4)
4-5
4-7
4
5-1 dfsR(G,1)
1-3 dfsR(G,3)
3-6 dfsR(G,6)
6-0 dfsR(G,0)
0-2
0-4
0
6-2
6-4
6
3
1
5-7
5
7-3
7
2
O rastreamento mostra que a permutação dos vértices em pós-ordem é 4 0 6 3 1 5 7 2. Portanto, post[] termina no seguinte estado:
v 4 0 6 3 1 5 7 2
post[v] 0 1 2 3 4 5 6 7
Para completar o exemplo, veja o estado final de pre[] e pa[] (com os vértices listados na ordem em que foram descobertos):
w 2 7 5 4 1 3 6 0
pre[w] 0 1 2 3 4 5 6 7
pa[w] 2 2 7 5 5 1 3 6
O rastreamento também mostra a relação entre os intervalos de vida das várias encarnações de dfsR():
2 7 5 4 4 1 3 6 0 0 6 3 1 5 7 2 ( ( ( ( ) ( ( ( ( ) ) ) ) ) ) )
Exemplo E. Considere o grafo não-dirigido representado pelas seguintes listas de adjacência:
0: 2 1 5 1: 0 2 2: 0 1 3 4 3: 5 4 2 4: 2 3 5: 0 3
Veja o rastreamento da execução de GRAPHdfs():
0 dfsR(G,0)
0-2 dfsR(G,2)
2-0
2-1 dfsR(G,1)
1-0
1-2
1
2-3 dfsR(G,3)
3-5 dfsR(G,5)
5-0
5-3
5
3-4 dfsR(G,4)
4-2
4-3
4
3-2
3
2-4
2
0-1
0-5
0
O rastreamento mostra que a permutação dos vértices em pós-ordem é 1 5 4 3 2 0. Portanto, post[] termina no seguinte estado:
v 1 5 4 3 2 0
post[v] 0 1 2 3 4 5
O estado final de pre[] e pa[] é o seguinte:
w 0 2 1 3 5 4
pre[w] 0 1 2 3 4 5
pa[w] 0 0 2 2 3 3
Veja também a relação entre os intervalos de vida das várias encarnações de dfsR():
0 2 1 1 3 5 5 4 4 3 2 0 ( ( ( ) ( ( ) ( ) ) ) )
0: 5 7 1: 5 2: 1 3: 4 6 4: 0 7 5: 2 7 6: 3 4 7: 1
intercalaras permutações em pré- e pós-ordem. Para isso, basta trocar a variável cntt por cnt, ou seja, usar o mesmo contador para registrar as descobertas e as mortes dos vértices. Desenvolva essa ideia. Quais as propriedades da
permutação duplade vértices correspondente à intercalação de pre[] e post[]? [Solução]
As relações genealógicas (ancestral, descendente, primo) entre os vértices de uma floresta DFS podem ser formuladas em termos dos intervalos de vida das várias encarnações de dfsR(). Um vértice x é ancestral de um vértice y se o intervalo de dfsR(G,x) contém o intervalo de dfsR(G,y); x é descendente de y se o intervalo de dfsR(G,x) está contido no intervalo de dfsR(G,y); x é primo esquerdo de y se o intervalo de dfsR(G,x) vem antes do de dfsR(G,y); x é primo direito de y se o intervalo de dfsR(G,x) vem depois do de dfsR(G,y).
Segue daí que a combinação das numerações em pré- e pós-ordem permite decidir, em tempo constante, a relação entre dois vértices da floresta DFS: para quaisquer dois vértices x e y,
A combinação de pre[] e post[] também permite decidir, em tempo constante, a classe de cada arco em relação à floresta DFS: para qualquer arco v-w que não pertence à floresta,
Note que se v-w é um arco cruzado então w é primo esquerdo de v. (Veja observação no capítulo Florestas DFS.) A seguinte tabela resume a caracterização dos arcos:
pre post
v w v w
< > floresta
< > avanço
> < retorno
> > cruzado
Grafos não-dirigidos não têm arcos cruzados. (Veja observação no capítulo Florestas DFS.) Portanto, para qualquer arco v-w de um grafo não-dirigido,
Exemplo F. Considere novamente o exemplo E. Veja os vetores pre[] e post[] daquele exemplo:
v 0 1 2 3 4 5
pre[v] 0 2 1 3 5 4
post[v] 5 0 4 3 2 1
(Desta vez os índices v estão listados em ordem crescente.) A partir desse par de vetores, obtemos a classificação dos arcos que não pertencem à floresta DFS:
0-1 avanço 0-5 avanço 1-0 retorno 1-2 retorno 2-0 retorno 2-4 avanço 3-2 retorno 4-2 retorno 4-3 retorno 5-0 retorno 5-3 retorno
Exemplo G. Considere novamente o exemplo D. Veja os vetores pre[] e post[] daquele exemplo:
v 0 1 2 3 4 5 6 7
pre[v] 7 4 0 5 3 2 6 1
post[v] 1 4 7 3 0 5 2 6
Deduzimos daí a classificação dos arcos que não pertencem à floresta:
0-2 retorno 0-4 cruzado 4-5 retorno 4-7 retorno 5-7 retorno 6-2 retorno 6-4 cruzado 7-3 avanço
Essa classificação também poderia ser produzida em tempo real (= on-the-fly), ou seja, no momento em que cada arco é percorrido:
2 dfsR(G,2) 2-7 dfsR(G,7) 7-5 dfsR(G,5) 5-4 dfsR(G,4) 4-5 retorno 4-7 retorno 4 5-1 dfsR(G,1) 1-3 dfsR(G,3) 3-6 dfsR(G,6) 6-0 dfsR(G,0) 0-2 retorno 0-4 cruzado 0 6-2 retorno 6-4 cruzado 6 3 1 5-7 retorno 5 7-3 avanço 7 2
Não é óbvio como produzir essa classificação em tempo real. A dificuldade está em decidir a classe de um arco v-w antes que os valores de pre[v], pre[w], post[v] e post[w] sejam todos conhecidos. Veja exercício abaixo.
v 0 1 2 3 4 5
pre[v] 0 1 5 4 2 3
post[v] 4 0 5 1 3 2