Algoritmos para Grafos  |  Índice

Grafos topológicos

Este capítulo apresenta uma importante classe de grafos: os grafos topológicos (também conhecidos como grafos topologicamente numerados, ou grafos topologicamente ordenados).  Grafos topológicos são como animais domesticados, enquanto grafos não topológicos são como animais selvagens.

A definição de grafos topológicos exige que os vértices sejam numerados de uma certa maneira.  Assim, cada grafo é acompanhado de uma numeração (= ranking) dos vértices, ou seja, uma atribuição de números inteiros aos vértices.  Essa numeração dos vértices será representada por um vetor cujos índices são vértices e cujos elementos são números inteiros.

Três tipos especiais de grafos topológicos também serão apresentados: as florestas radicadas, as árvores radicadas, e os grafos bipartidos dirigidos.

Grafos topológicos

Um grafo é topológico se admite uma numeração topológica dos vértices.   Uma numeração topo[] dos vértices é topológica se

topo[v] < topo[w]

para todo arco v-w. (Note que a numeração dos vértices não tem relação alguma com os nomes 0 1 ... V-1 dos vértices.)  Se os vértices do grafo forem dispostos ao longo de um linha vertical em ordem crescente da numeração topológica, todos os arcos apontarão para baixo.  A seguinte função recebe uma numeração topo[0..V-1] de um grafo G representado por listas de adjacência e decide se essa numeração é topológica:

bool isTopoNumbering( Graph G, int topo[]) {
   for (vertex v = 0; v < G->V; ++v) 
      for (link a = G->adj[v]; a != NULL; a = a->next) 
         if (topo[v] >= topo[a->w]) 
            return false;
   return true;
}

A maioria dos grafos não tem numeração topológica. Por outro lado, um grafo pode ter várias numerações topológicas diferentes.

Exemplo A.  Como os vértices de nossos grafos são números inteiros, podemos compará-los.  Se  v < w  para todo arco v-w então o grafo é topológico. A numeração topológica nesse caso é a identidade:  topo[v] ≡ v para cada v.

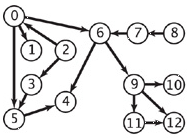
Exemplo B.  As duas figuras abaixo representam o mesmo grafo. A segunda sugere a numeração topológica dada pelo seguinte vetor:

     v   0  1  2  3  4  5  6  7  8  9 10 11 12
topo[v]  4 10  2  3 12 11  5  1  0  6  7  8  9

Propriedades.  Eis três propriedades importantes de grafos topológicos:

1. Grafos topológicos não têm ciclos.
2. Todo vértice de um grafo topológico é término de um caminho que começa numa fonte.
3. Todo vértice de um grafo topológico é origem de um caminho que termina num sorvedouro.

As três propridades são quase óbvias. Segue imediatamente das propriedades 2 e 3 que todo grafo topológico tem pelo menos uma fonte e pelo menos um sorvedouro.  (A recíproca da primeira propriedade é verdadeira, mas a tecnologia necessária para provar essa recíproca só será desenvolvida nos próximos capítulos.)

Grafos topológicos aparecem naturalmente em muitas aplicações. Imagine, por exemplo, que cada vértice é uma tarefa de um grande projeto e que um arco v-w indica que a tarefa w só pode começar depois que a tarefa v tiver sido concluída. Imagina também que o projeto está a cargo de alguém que só pode executar uma tarefa por vez.  Nesse caso, uma numeração topológica dá uma possível ordem de execução das tarefas.  (Um exemplo concreto: a primeira providência do utilitário make é construir o grafo de dependências das tarefas e obter uma numeração topológica dos vértices do grafo.)

Variantes.  Grafos topológicos podem ser discutidos em termos de três conceitos equivalentes ao de uma numeração topológica:

• Uma numeração atopo[] dos vértices de um grafo é anti-topológica se  atopo[v] > atopo[w]  para todo arco v-w.  É claro que uma numeração atopo[] é anti-topológica se e somente se, para qualquer constante M, a numeração definida por M - atopo[v] for topológica.
• Uma permutação  v₀ v₁ … v_n−1  do conjunto de vértices de um grafo é topológica se  i  <  j  para todo arco v_i – v_j , ou seja, se todos os arcos apontam da esquerda para a direita.  Toda permutação topológica é o inverso de uma numeração topológica.
• Uma permutação  v₀ v₁ … v_n−1  do conjunto de vértices de um grafo é anti-topológica se v_n−1 … v₁ v₀  é uma permutação topológica.

Esses três conceitos têm a mesma força que uma numeração topológica:  um grafo tem uma numeração topológica se e somente se tem uma numeração anti-topológica, se e somente se tem uma permutação topológica, se e somente se tem uma permutação anti-topológica.

Exemplo C.  Veja a permutação topológica que corresponde à numeração topo[] do exemplo B:

     i   0  1  2  3  4  5  6  7  8  9 10 11 12
perm[i]  8  7  2  3  0  6  9 10 11 12  1  5  4

Um algoritmo de numeração topológica

Como encontrar uma numeração topológica de um grafo?  O seguinte algoritmo de eliminação iterada de fontes responde a pergunta. Remova uma fonte do grafo; depois remova uma fonte do grafo resultante; e assim sucessivamente.  (Em outras palavras, remova fontes recursivamente.)  Numere os vértices — 0, 1, 2, etc. — à medida que são removidos.  Se todos os vértices forem removidos, a numeração é topológica; senão, não existe numeração topológica.

A justificativa do algoritmo é simples. Note que um vértice v é removido e numerado somente depois que forem removidos e numerados todos os vértices u tais que u-v é um arco. Logo, se ambas as pontas de um arco u-v estão numeradas então o número de u é menor que o número de v. Portanto, se todos os vértices são numerados então a numeração é topológica.  Suponha agora que o algoritmo termina antes que todos os vértices sejam numerados e removidos. Nesse caso, o grafo restante não tem fontes. Como todo grafo topológico tem pelo menos uma fonte, o grafo restante não é topológico. Segue daí que o grafo original também não era topológico.

Segue uma implementação ao pé da letra do algoritmo de eliminação de fontes. Como nossa estrutura de dados tem dificuldade em lidar com remoção de vértices, a implementação remove arcos:

int topo[1000];

bool topol( Graph G) { 
   // implementação muito ineficiente...
   for (vertex v = 0; v < G->V; ++v) topo[v] = -1;
   int cnt = 0;
   while (cnt < G->V) {
      for (vertex v = 0; v < G->V; ++v) 
         if (GRAPHindeg( G, v) == 0 && topo[v] == -1)
            break;
      if (v >= G->V) return false;
      // v é fonte
      topo[v] = cnt++;
      for (link a = G->adj[v]; a != NULL; a = a->next)
         GRAPHremoveArc( G, v, a->w);
   }
   return true;
}

A função é muito ineficiente. Num grafo com V vértices e A arcos, cada invocação de GRAPHindeg() consome V+A unidades de tempo e portanto cada vez que topol() procura uma fonte, gasta V(V+A) unidades de tempo no pior caso. Como tudo é repetido V vezes, temos um consumo total de V²(V+A). É muito lento!  Além disso, essa implementação ao pé da letra tem o efeito indesejável de destruir o grafo.

Para fazer uma implementação eficiente do algoritmo, podemos remover arcos virtualmente, mantendo atualizado um vetor indeg[] com os graus de entrada virtuais dos vértices. Se indeg[v] ≡ 0 então v é uma fonte virtual.  Além disso, para que não percamos tempo procurando essas fontes virtuais, podemos mantê-las numa fila.

int topo[1000];

bool GRAPHtopol( Graph G) { 
   int indeg[1000];
   for (vertex v = 0; v < G->V; ++v) indeg[v] = 0;
   for (vertex v = 0; v < G->V; ++v) 
      for (link a = G->adj[v]; a != NULL; a = a->next)
         indeg[a->w] += 1;
   vertex fila[1000]; 
   int comeco = 0, fim = 0;
   for (vertex v = 0; v < G->V; ++v)
      if (indeg[v] == 0) 
         fila[fim++] = v;
   int cnt = 0;
   while (comeco < fim) { 
      // fila[comeco..fim-1] contém as fontes virtuais
      vertex v = fila[comeco++];
      topo[v] = cnt++;
      for (link a = G->adj[v]; a != NULL; a = a->next) {
         indeg[a->w] -= 1; // remoção virtual do arco v-w
         if (indeg[a->w] == 0) 
            fila[fim++] = a->w;
      }
   }
   return cnt >= G->V;
}

Essa implementação é muito rápida: consome apenas V+A unidades de tempo, mesmo no pior caso.

Florestas radicadas

Uma floresta radicada é um grafo topológico sem vértices com grau de entrada maior que 1.  (O adjetivo radicada é importante; a palavra floresta sem o adjetivo está reservada para a versão não-dirigida do conceito.)

(É tentador pensar que florestas radicadas podem ser definidas sem referência a grafos topológicos. É tentador imaginar que todo grafo com pelo menos uma fonte e sem vértices de grau de entrada maior que 1 é uma floresta radicada. Mas isso não é verdade.)

Exemplo D.  A figura mostra uma floresta radicada com arcos  4-5 5-0 5-1 ... 7-9 7-10.  O seguinte vetor exibe a numeração topológica sugerida pela figura:

     v    0 1 2 3 4 5 6 7 8 9 10 11
topo[v]   2 2 3 3 0 1 1 1 2 2  2  0

Veja uma numeração topológica diferente:

     v    0 1 2 3 4 5 6 7 8  9 10 11
topo[v]   2 5 3 4 0 1 7 8 9 10 11  6

Propriedades.  É claro que florestas radicadas não têm ciclos. É claro também que todo vértice de uma floresta radicada é término de um caminho que começa em uma fonte, e todo vértice é origem de um caminho que termina em um sorvedouro. Além disso, florestas radicadas têm a seguinte propriedade adicional, facilmente deduzida da definição:

• todo vértice de uma floresta radicada é término de um único caminho que começa numa fonte.

Segue daí imediatamente que, para quaisquer dois vértices x e y, existe no máximo um caminho de x a y. Ademais, se existe um caminho de x a y então não existe caminho de y a x.

Terminologia.  Usamos uma terminologia natural e sugestiva para falar sobre florestas radicadas:

• As fontes de uma floresta radicada são chamadas raizes.
• Os sorvedouros de uma floresta radicada são chamados folhas.
• Cada vizinho de um vértice v é um filho de v.  (Aqui, os conceitos filho esquerdo e filho direito que aparecem na estrutura de dados conhecida como árvore binária não fazem sentido.)
• Com exceção de uma raiz, todo vértice w de uma floresta radicada tem um pai:  trata-se do único vértice v do qual w é filho.
• Um vértice u é ancestral de um vértice z se existe um caminho u a z;  um ancestral de z é próprio se for diferente de z.
• Um vértice z é descendente de um vértice u se u é ancestral de z;  um descendente de u é próprio se for diferente de u.
• Um primo de um vértice u é qualquer vértice que não seja ancestral nem descendente de u.

O vetor de pais (= parent array) de uma floresta radicada é um vetor que associa a cada vértice (exceto uma raiz) o seu pai.  Se p[] é um vetor de pais e w não é uma raiz, então p[w] é o pai de w.  Se w é uma raiz, adotamos a convenção p[w] ≡ w.  Para qualquer vértice w, a sequência

w  p[w]  p[p[w]]  p[p[p[w]]]  ...

termina necessariamente em uma raiz.  Diremos que essa sequência é a regressão (= recessional sequence) de w.  O inverso dessa sequência é o caminho que leva da raiz a w (passando por todos os ancestrais de w).  Por exemplo, a floresta radicada exemplo D tem o seguinte vetor de pais:

  v    0  1  2  3  4  5  6  7  8  9 10
p[v]   5  5  0  0  4  4 11 11  7  7  7

A profundidade de um vértice w numa floresta radicada é o comprimento do único caminho que começa em alguma raiz e termina em w.  A altura da floresta radicada é a profundidade de um vértice de profundidade máxima. (É claro que um vértice de profundidade máxima é uma folha.)

Árvores radicadas

Uma árvore radicada (= branching) é uma floresta radicada que tem uma só raiz.  (O adjetivo radicada é importante; a palavra árvore sem o adjetivo está reservada para a versão não-dirigida do conceito.)

Propriedades.  Segue imediatamente das propriedades de florestas radicadas que todo vértice de uma árvore radicada é término de um e um só caminho que começa na única raiz.  Segue também que toda floresta radicada consiste em uma ou mais árvores radicadas, cada árvore radicada correspondendo a uma das raízes da floresta.

Toda a terminologia definida para florestas radicadas — folha, pai, filho, ancestral, descendente, primo — aplica-se igualmente bem a árvores radicadas.  O conceito de vetor de pais também se aplica a árvores radicadas.  Por exemplo,

  v    0 1 2 3 4 5 6 7 8 9 10 11 12 13
p[v]   3 2 4 4 4 0 3 2 0 1  1  0  6  2

é o vetor de pais da árvore radicada no seguinte exemplo.

Exemplo E.  A figura mostra uma árvore radicada com arcos  4-2 4-3 ... 0-5 0-8  e numeração topológica dada pelo seguinte vetor:

     v    0 1 2 3 4 5  6 7  8 9 10 11 12 13
topo[v]  10 3 1 7 0 12 8 6 13 5  4 11  9  2

Grafos bipartidos dirigidos

Um grafo é bipartido dirigido se tiver uma numeração topológica com apenas dois valores: 0 e 1.  (Não confunda grafo bipartido dirigido com bipartido não-dirigido.)  Em outras palavras, um grafo é bipartido dirigido se existe uma numeração topo[] dos vértices tal que, para cada arco v-w, topo[v] vale 0 e topo[w] vale 1.

Grafos bipartidos dirigidos aparecem naturalmente em muitas situações.  Imagine, por exemplo, que alguns vértices representam pessoas, outros vértices representam clubes, e um arco v-w significa que a pessoa v é membro do clube w.  Uma versão mais concreta desse exemplo: alguns vértices representam filmes de cinema, outros representam atores e atrizes, e um arco v-w significa que o ator/atriz w teve um papel no filme v.

Propriedade.  Grafos bipartidos dirigidos têm uma propriedade óbvia: todo vértice é uma fonte ou um sorvedouro.

Exemplo F.  O grafo com vértices 0 1 2 3 4 e arcos  0-2 0-3 1-3 1-4  é bipartido dirigido. O seguinte vetor topo[] define a numeração topológica apropriada:

     v    0 1 2 3 4
topo[v]   0 0 1 1 1