Grafos não-dirigidos bipartidos versus circuitos ímpares

Muitos grafos não-dirigidos são naturalmente bipartidos: imagine, por exemplo, que alguns vértices representam pessoas à procura de emprego, outros representam empresas que oferecem empregos, e as arestas indicam que há compatibilidade entre um vértice do primeiro tipo e um do segundo.

Bipartição do conjunto de vértices

Uma bipartição, ou bicoloração, de um grafo não-dirigido é uma coloração válida do grafo com duas cores. (Eu poderia dizer bicoloração válida, mas é melhor deixar o válida subentendido.) Portanto, uma bicoloração é uma atribuição de uma de duas cores — preto e vermelho, por exemplo — a cada vértice do grafo de tal modo que as duas pontas de cada aresta tenham cores diferentes.

Um grafo não-dirigido é bipartido, ou bicolorido, se admite uma bicoloração. (Não confunda esse conceito com o conceito bem mais simples de grafo bipartido dirigido!)

Eis uma pequena aplicação: Uma indústria química tem dois galpões para armazenar seu estoque de reagentes. Por segurança, certos pares de reagentes devem ficar separados. É possível distribuir os reagentes pelos dois galpões de modo a separar os que são incompatíveis?

Exercícios 1

Faça uma lista de todas as diferenças entre o conceito de grafo não-dirigido bipartido e o conceito de grafo bipartido dirigido.
O grafo definido pelo conjunto de arestas 0-1 1-2 2-3 3-0 0-4 4-5 5-2 admite bicoloração? O grafo definido pelo conjunto de arestas 0-1 1-2 2-3 3-0 4-6 0-5 5-2 é bipartido?
Os grafos da figura admitem bipartição?
Grade. Mostre que toda grade não-dirigida é bicolorida.
Cubo. Mostre que, para qualquer n, o cubo de dimensão n é bicolorido.
★ Bipartição e distâncias (parte I). Seja s um vértice qualquer de um grafo não-dirigido conexo G. Para cada vértice x, denote por d(x) a distância de s a x. Suponha que d(v) ≠ d(w) para cada aresta v-w. Prove que G é bipartido. (Dica: veja a paridade de d(v).)
Bipartido aleatório. Escreva uma função que construa um grafo não-dirigido bipartido aleatório com V₁ vértices de uma cor, V₂ vértices da outra, e E arestas.

Algoritmo de bipartição

O seguinte algoritmo recursivo A decide se um grafo não-dirigido conexo G admite bicoloração. O algoritmo é bastante ingênuo. Ele supõe dada uma bicoloração incompleta de G, que pode ser vazia. O algoritmo recebe um vértice incolor v e uma cor c e decide — sim ou não — se existe uma bicoloração (completa) de G que estende a bicoloração incompleta e atribui cor c a v:

A seguinte função implementa o algoritmo para qualquer grafo não-dirigido, conexo ou não. A função tenta produzir uma bicoloração dos vértices fazendo uma busca em profundidade. Ela só fracassa se o grafo não tem bicoloração alguma.

#define UGraph Graph
int color[1000];

/* A função decide se o grafo não-dirigido G admite bipartição.
   Em caso afirmativo, a função
   atribui uma cor, 0 ou 1, 
   a cada vértice de G de tal forma
   que toda aresta tenha pontas de cores diferentes. 
   As cores dos vértices são armazenadas no vetor color[] 
   indexado pelos vértices. 
   (Esta função supõe que G é representado por listas de adjacência.
   Código inspirado no programa 18.6 de Sedgewick.) */

bool UGRAPHtwoColor( UGraph G)
{ 
   for (vertex v = 0; v < G->V; ++v) 
      color[v] = -1; // incolor
   for (vertex v = 0; v < G->V; ++v)
      if (color[v] == -1) // começa nova etapa
         if (dfsRtwoColor( G, v, 0) == false) 
            return false;
   return true;
}

/* Decide se existe uma bicoloração de G 
   que atribui cor c ao vértice v

   e estende a bicoloração incompleta color[]
   à componente conexa de G que contém v. */

static bool dfsRtwoColor( UGraph G, vertex v, int c)
{ 
   color[v] = c;
   for (link a = G->adj[v]; a != NULL; a = a->next) {
      vertex w = a->w; 
      if (color[w] == -1) {
         if (dfsRtwoColor( G, w, 1-c) == false) 
            return false; 
      }
      else { // v-w é de avanço ou de retorno
         if (color[w] == c) // base da recursão
            return false;
      }
   }
   return true;
}

Se a função devolve true, é fácil entender que color[] representa uma bicoloração e portanto G é bipartido. Resta mostrar que se a função devolve false então G não admite bicoloração alguma. Faremos isso na próxima seção.

Exemplo A. Aplique a função GRAPHtwoColor() ao grafo da figura. Suponha que as listas de adjacência de todos os vértices estão em ordem crescente. Veja o rastreamento da execução da função.

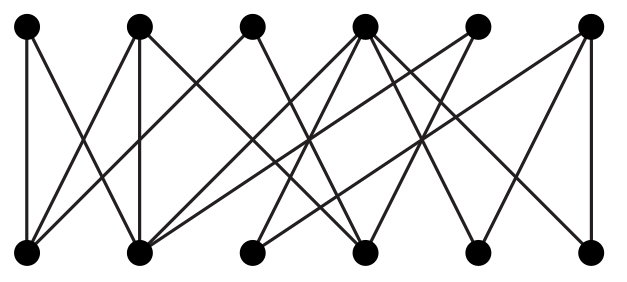
Exemplo B. Aplique a função GRAPHtwoColor() ao grafo definido pelas listas de adjacência abaixo. (Imagine que os vértices da figura estão numerados no sentido horário a partir do nordeste.)

Desempenho. Quando aplicada a um grafo não-dirigido com V vértices e E arestas, a função UGRAPHtwoColor() consome tempo proporcional a V + E no pior caso. (Se o grafo é conexo, como acontece em muitas aplicações, podemos dizer que o consumo de tempo é proporcional a E.) O algoritmo é, portanto, linear.

Exercícios 2

Quantas etapas tem UGRAPHtwoColor() se for aplicado a um grafo conexo?
Suponha que a função UGRAPHtwoColor() devolve true ao receber um grafo não-dirigido G. Mostre que o vetor color[] contém uma bicoloração de G.
Florestas. Mostre que toda floresta é bicolorida. (Dica: analise o código de UGRAPHtwoColor().)

Circuitos ímpares

Um circuito num grafo não-dirigido é ímpar (= odd) se seu comprimento for um número ímpar. Se um grafo tem um circuito ímpar, então é óbvio que não admite bipartição. A recíproca é menos óbvia, como veremos a seguir.

Suponha que um grafo não-dirigido G não admite bipartição. Então a função UGRAPHtwoColor() acima devolve false quando recebe G. Portanto, dois vértices v e w de G têm a mesma cor em alguma execução da linha if (color[w] == c) do código. Observe que o arco v-w é de avanço ou de retorno, uma vez que o grafo é não-dirigido. Suponha, primeiramente, que v-w é de retorno. Seja w-x-y-...-u-v o caminho de w a v na floresta DFS. O comprimento do caminho é par, uma vez que v e w têm a mesma cor e as cores dos vértices se alternam ao longo do caminho. Portanto, w-x-y-...-u-v-w é um circuito ímpar. Suponha agora que v-w é de avanço. Então um raciocínio análogo ao anterior mostra que o arco w-v pertence a um circuito ímpar. Conclusão: Se a função G não tem uma bicoloração então o grafo tem um circuito ímpar.

Exercícios 3

Critique a seguinte pergunta-e-resposta: O que é um grafo bipartido? Um grafo bipartido é um grafo sem circuitos ímpares.
Considere as seguintes afirmações: (1) grafo bipartidos não têm circuitos ímpares e (2) grafos sem circuitos ímpares são bipartidos. Qual dessas duas afirmações é óbvia? Qual não é óbvia?
Critique o seguinte afirmação: Este grafo tem um circuito de comprimento 101. Podemos dizer então, com base em um teorema bem conhecido, que o grafo não é bicolorido.
Óbvio. Suponha que um grafo não-dirigido tem um circuito ímpar. Mostre que o grafo não admite bipartição.
O grafo da figura admite bipartição?
Acrescente código a UGRAPHtwoColor() para construir uma floresta DFS durante a busca. Em seguida, mostre que color[v] ≠ color[w] para todo arco v-w da floresta. Deduza daí que as cores dos vértices são alternadamente 0 e 1 ao longo de qualquer caminho na floresta.
Bipartição ou circuito ímpar. Expanda o código de UGRAPHtwoColor() de modo que a função devolva um circuito ímpar se não obtiver uma bipartição. (Dica: Ao fazer a busca em profundidade, construa o vetor de pais pa[] de uma floresta DFS; ao encontrar um arco v-w de um circuito ímpar, faça pa[w] = v e devolva w; o vetor pa[] junto com o vértice w representarão o circuito.) (Compare com o exercício Ciclo e permutação topológica explícitos.)

Exercícios 4

★ Bipartição e distâncias (parte II). Seja s um vértice qualquer de um grafo não-dirigido conexo G. Para cada vértice x, denote por d(x) a distância de s a x. Suponha que G é bicolorido e mostre que d(v) ≠ d(w) para cada aresta v-w.
Seja s um vértice de um grafo não-dirigido conexo G e d[] um vetor indexado pelos vértices tal que d[v] é a distância de s a v em G. Escreva um função booleana que receba G e d[] e decida se G é bipartido. Explique brevemente por que sua função está correta.
★ Bipartição via busca em largura. Escreva uma função que use busca em largura para tentar fazer a bicoloração dos vértices de um grafo não-dirigido. (Sugestão: Suponha que o grafo é conexo. Escolha um vértice s e calcule, para cada vértice x, a distância d(x) de s a x. Se d(v) = d(w) para alguma aresta v-w temos um circuito ímpar. Senão, o grafo admite bipartição.) Expanda o seu código de modo que a função devolva um circuito ímpar se o grafo não tiver bipartição.

Conclusão

Este capítulo traz mais uma caracterização demonstrada por um algoritmo. Eis as duas caracterizações desse tipo vistas até aqui:

Perguntas e respostas

Pergunta: Não seria mais correto dizer biparticionável no lugar de bipartido? Não seria mais correto dizer bicolorível no lugar de bicolorido?
Resposta: Certo! Eu deveria dizer que um grafo é bicolorido somente quando uma bicoloração do grafo é dada explicitamente. Da mesma forma, eu deveria dizer bipartido somente quando uma bipartição é dada explicitamente. Mas essa sutileza linguística é tradicionalmente ignorada na literatura da teoria dos grafos.
Pergunta: Por que não dizer bicromático no lugar de bicolorido e bicolorível?
Resposta: Parece muito razoável. Mas a tradição da teoria dos grafos reserva o adjetivo bicromático a grafos que têm uma bicoloração mas não têm uma coloração com apenas uma cor (ou seja, têm pelo menos uma aresta).

Grafos bipartidos e circuitos ímpares