O problema da coloração dos vértices de um grafo

Este capítulo apresenta o importante problema da coloração dos vértices de grafos não-dirigidos. Como não se conhecem bons algoritmos para o problema, vamos nos limitar a examinar algumas heurísticas simples.

O problema

Uma coloração dos vértices de um grafo não-dirigido é uma atribuição de cores aos vértices tal que cada vértice recebe uma e uma só cor. Portanto, uma coloração nada mais é que uma numeração dos vértices. Podemos dizer também que uma coloração é uma partição do conjunto de vértices: cada bloco da partição corresponde a uma cor.

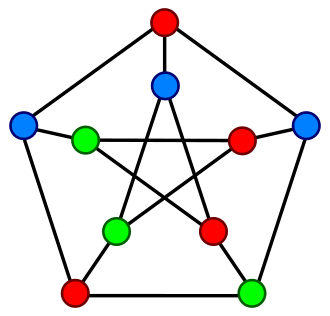
Uma coloração de um grafo é válida se as duas pontas de cada aresta têm cores diferentes. (Quando o contexto permite, dizemos coloração de um grafo, deixando a expressão dos vértices subentendida.) A figura ao lado mostra um grafo não-dirigido e uma coloração válida com 3 cores. Uma bicoloração é uma coloração válida com 2 cores.

A expressão coloração com k cores não significa que todas as k cores são usadas; significa apenas que o número de cores não passa de k. Portanto, uma coloração válida com k cores também é uma coloração válida com k +1 cores. A propósito, dizemos que um grafo é k-colorível se tem uma coloração válida com k cores.

Encontrar colorações válidas com muitas cores (tantas quantas são os vértices, por exemplo) é fácil. Encontrar colorações válidas com poucas cores é bem mais difícil.

Vale a pena mencionar a seguinte variante do problema: dado um grafo não-dirigido G e um inteiro k, encontrar uma coloração válida de G com k cores. (É claro que nem toda instância dessa variante tem solução.) Essa variante é computacionalmente equivalente ao problema da coloração mínima, embora isso não seja imediatamente aparente.

É fácil provar que um grafo é k-colorível: basta exibir uma coloração válida com k cores. Mas como provar que um dado grafo não é k-colorível? Essa questão está na base da dificuldade do problema da coloração.

Exemplo A. Uma indústria química precisa armazenar os reagentes que tem em estoque. Por razões de segurança, alguns pares de reagentes não podem ficar no mesmo galpão. Qual o número mínimo de galpões necessário para armazenar todos os reagentes? Nesse exemplo, cada reagente é um vértice do grafo, reagentes incompatíveis definem as arestas, e cada galpão é uma cor.

Exemplo B. O quebra-cabeça Sudoku consiste em preencher uma matriz 9-por-9 com os números 1 2 3 ... 9 de tal forma que cada linha seja uma permutação de 1..9, cada coluna seja uma permutação de 1..9 e cada uma das nove submatrizes 3-por-3 com borda mais escura seja uma permutação de 1..9. Esse quebra-cabeça é uma instância do problema da coloração mínima. Os vértices do grafo são as 81 casas da matriz e dois vértices são vizinhos se estiverem na mesma linha, ou na mesma coluna, ou na mesma submatriz 3-por-3 com borda escura. O desafio está em obter uma coloração válida com as cores 1 2 3 ... 9. Para tornar o Sudoku mais interessante, a matriz é apresentada com uma coloração incompleta (números pretos na figura) e o desafio é completar essa coloração incompleta (números vermelhos na figura).

Exercícios 1

Como são os grafos não-dirigidos que podem ser coloridos com apenas uma cor? Como são os grafos não-dirigidos que têm uma coloração válida com 2 cores? Como são os grafos não-dirigidos 3-coloríveis?
★ Verificação. Escreva uma função que receba um grafo não-dirigido G e um vetor indexado pelos vértices e verifique se esse vetor é uma coloração válida de G.
Suponha dadas duas colorações com k cores de um mesmo grafo. Em que condições é razoável dizer que as duas colorações são diferentes? É verdade que todo grafo k-colorível tem uma única coloração com k cores?
Coloração mínima versus k-coloração. Mostre que o problema da coloração mínima é computacionalmente equivalente ao problema da k-coloração (em que o número k de cores é um dado do problema). Em outras palavras, mostre que qualquer algoritmo para um dos problemas pode ser transformado num algoritmo para o outro de modo que o algoritmo derivado seja basicamente tão rápido quanto o original. (Dica: Numa das direções, use busca binária.)
Grade com diagonais. Seja G o seguinte grafo não-dirigido: comece com um grade não-dirigida; depois, acrescente diagonais noroeste-sudeste a todos os pequenos quadrados. Mostre que G admite uma coloração válida com 3 cores. É verdade que G não tem coloração válida com apenas 2 cores?
Grade com diagonais aleatórias. Seja G o grafo não-dirigido definido da seguinte maneira: comece com um grade não-dirigida; depois, acrescente diagonais a todos os pequenos quadrados; a orientação de cada diagonal — noroeste-sudeste ou sudoeste-nordeste — é escolhida aleatoriamente. Esse grafo admite uma coloração válida com 3 cores?
Grafo cúbico aleatório. Construa um grafo não-dirigido aleatório cada um de cujos vértices tem grau menor que 4. Quantas cores são necessárias para uma coloração válida do grafo? Quantas cores são suficientes para uma coloração válida do grafo?
★ Grafo de Catlin. Encontre uma coloração válida mínima dos vértices do grafo definido da seguinte maneira: comece com cinco cópias mutuamente disjuntas, digamos B₁, … , B₅, de um grafo completo com 3 vértices; para cada i, acrescente arestas ligando todos os vértices de B_i a todos os de B_i+1; finalmente, acrescente arestas ligando todos os vértices de B₅ a todos os de B₁.
Quantas cores são necessárias para colorir os grafos das figuras à direita?
Grafos planares e suas 4 cores. Um grafo é planar se pode ser desenhado no plano sem que as linhas que representam as arestas se cruzem. Todo grafo planar tem uma coloração válida com 4 cores. Esse fato foi demonstrado em 1976 depois de um século de tentativas frustradas. A demonstração é muito difícil.

Algoritmos

Para encontrar uma coloração válida de um grafo com k de cores poderíamos simplesmente fazer uma lista de todas as colorações com k cores e eliminar, sistematicamente, as que não são válidas. Mas esse algoritmo força bruta é extremamente lento, pois o número de colorações cresce exponencialmente com o número de vértices do grafo.

Um algoritmo rápido para o problema da coloração mínima ainda não foi descoberto. Suspeita-se mesmo que um tal algoritmo não existe. Em vista disso, trataremos neste capítulo apenas de algumas heurísticas simples. Essas heurísticas produzem colorações válidas mas em geral usam mais cores que o mínimo necessário.

Exercícios 2

Seja G um grafo não-dirigido com V vértices. Quantas são as colorações de G com k cores?
★ Backtracking. Escreva um algoritmo que examine, sistematicamente, todas a possíveis colorações de um grafo com k cores até encontrar uma que seja válida (ou constatar que não existe k-coloração válida). Use as ideias da busca em profundidade: cada chamada da função recursiva recebe com uma k-coloração válida incompleta (como no Sudoku) e procura encontrar uma coloração válida completa que contenha a coloração dada.
Desafio da tricoloração. Invente um algoritmo rápido que decida se um grafo não-dirigido admite uma coloração válida com 3 cores.
Desafio: certidão negativa de tricoloração. Invente uma boa maneira de mostrar que um grafo não é 3-colorível. (Talvez um vértice de grau elevado ou então um subgrafo completo com 4 vértices?)

Uma heurística gulosa

A seguinte heurística, conhecida como algoritmo de coloração sequencial, produz uma coloração válida de qualquer grafo. No início de cada iteração, temos uma coloração válida incompleta que usa as cores 0 1 2 ... k−1. Cada iteração consiste no seguinte:

Em geral, cada iteração tem vários candidatos para o papel de c, ou seja, tem mais de uma cor disponível para o vértice v. O algoritmo escolhe qualquer uma das cores disponíveis, sem medir as consequências que essa escolha terá em iterações futuras (note que o algoritmo não pode se arrepender e mudar uma escolha feita no passado). Esse comportamento é conhecido como guloso (= greedy).

#define UGraph Graph

/* Esta função calcula uma coloração válida dos vértices 
   do grafo não-dirigido G
   e devolve o número de cores usadas.
   A coloração é armazenada no vetor color[]. */

int UGRAPHseqColoring( UGraph G, int *color)
{ 
   int k = 0;
   for (vertex v = 0; v < G->V; ++v) color[v] = -1;

   for (vertex v = 0; v < G->V; ++v) {
      // as cores são 0..k-1
      bool available[100];
      int c; 
      for (c = 0; c < k; ++c) available[c] = true;
      for (link a = G->adj[v]; a != NULL; a = a->next) {
         if (color[a->w] != -1)
            available[color[a->w]] = false;
      } // A
      c = 0;
      while (c < k && !available[c]) ++c;
      if (c < k) color[v] = c;
      else color[v] = k++;
   }
   return k;
}

No início de cada iteração, o conjunto de cores é 0..k-1. No ponto A, available[0..k-1] é o vetor característico do conjunto de cores disponíveis para o vértice v.

É claro que a coloração produzida pelo algoritmo é válida. Mas o número de cores pode ser bem maior que o mínimo necessário. Assim, do ponto de vista do problema da coloração mínima, esse algoritmo guloso é apenas uma heurística.

Exemplo C. Considere o grafo com conjunto de arestas 0-3 3-5 5-1 1-6 6-4 4-2. Aplique a função UGRAPHseqColoring() a esse grafo. Veja o estado do vetor color[] no início de cada iteração:

Exercícios 3

Para que serve o algoritmo de coloração sequencial? Que problema resolve?
★ Como começa cada iteração do algoritmo de coloração sequencial? (Cuidado! Não quero uma descrição das ações que ocorrem no início de uma iteração! Quero saber, isso sim, quais as informações disponíveis no início de uma iteração genérica, antes que a execução da iteração comece.)
Instâncias extremas. A primeira iteração da função UGRAPHseqColoring() (no começo dessa iteração k vale 0) está correta? A segunda iteração está correta? A função produz uma coloração válida quando o grafo tem apenas um ou dois vértices? Produz uma coloração válida quando o grafo não tem arestas? Produz uma coloração válida quando o grafo é completo? Quantas cores a função usa em cada um desses casos extremos?
Quantas cores a função UGRAPHseqColoring() usa para colorir um grafo não-dirigido bicolorível.
★ Mostre que a função UGRAPHseqColoring() usa no máximo Δ+1 cores, sendo Δ o grau de um vértice de grau máximo. (Portanto, basta que o vetor available[] tenha Δ elementos.)
Aplique a função UGRAPHseqColoring() à grade com diagonais.
Dê um exemplo em que a função UGRAPHseqColoring() usa muito mais cores que o mínimo necessário.
★ Versão aleatorizada. Em cada iteração de UGRAPHseqColoring(), escolha aleatoriamente uma das cores disponíveis para o vértice v. Faça experimentos para verificar a eficácia dessa estratégia. Outra possibilidade: examine os vértices em ordem aleatória. Faça experimentos para verificar a eficácia dessa estratégia.
★ Graus decrescentes. A experiência sugere que o algoritmo de coloração sequencial tende a usar menos cores se os vértices forem examinados em ordem decrescente de graus. Implemente essa versão do algoritmo.
★ Heurística de Brélaz. Esta é uma variante do algoritmo de coloração sequencial. Suponha dada uma coloração válida incompleta de um grafo não-dirigido G e suponha que o conjunto de cores é 0 1 2 ... k-1. Em cada iteração, escolha um vértice incolor v que seja adjacente ao maior número de cores. Em caso de empate, escolha o vértice que tiver maior grau. Aplique a v a menor cor que seja diferente das cores usadas nos vizinhos de v. Implemente esse algoritmo. Faça experimentos para avaliar a eficácia do algoritmo.
Mostre que a heurística de Brélaz usa o número mínimo de cores quando aplicada a um grafo não-dirigido bicolorível.

Troca de cores em componentes bicoloridas

Para fugir do caráter guloso do algoritmo de coloração sequencial, podemos permitir que o algoritmo reveja decisões tomadas em iterações anteriores.

Suponha dada uma coloração válida incompleta do grafo não-dirigido G e um vértice v que ainda não foi colorido. Suponha que dispomos de k cores apenas e que cada uma das cores é usada na vizinhança de v. É possível alterar a coloração corrente de modo que alguma das cores saia da vizinhança de v e assim fique disponível para v? Eis uma heurística da troca de cores em componentes bicoloridas que pode fazer isso.

Suponha, para simplificar, que a cor 0 aparece uma só vez na vizinhança de v. Digamos que w é o vizinho de v que tem cor 0. Seja X o conjunto dos vértices que têm cor 0 ou 1 e considere o subgrafo não-dirigido G[X] induzido por X. (Veja o exercício Componentes de subgrafos induzidos no capítulo Componentes conexas.) Suponha que a componente conexa de G[X] que contém w não contém nenhum dos vizinhos de v que têm cor 1. Nesse caso, se intercambiarmos as cores 0 e 1 em X, a cor 0 ficará disponível para v!

Essa heurística pode, às vezes, reduzir o número de cores usado pelo algoritmo de coloração sequencial. (Em geral, entretanto, a heurística não produz uma coloração válida com número mínimo de cores.)

Exemplo D. Considere a coloração válida incompleta do grafo grade da figura. Os números 0 1 2 indicam as cores. Digamos que o vértice v não tem cor. Como esse vértice tem vizinhos de cores 0, 1 e 2, não pode receber nenhuma dessas cores.

Os vizinhos de v, em sentido horário a partir do oeste, são w x y z. A componente das cores 0 e 1 que contém w não contém y. Portanto, se intercambiarmos as cores 0 e 1 na componente que contém w, a cor 0 ficará disponível para v. (Tente repetir esse truque com outros pares de cores e outros vizinhos de v.)

Exercícios 4

★ Troca de cores em componentes bicoloridas. Implemente o algoritmo de coloração sequencial combinado com a heurística da troca de cores em componentes bicoloridas. Faça experimentos para avaliar a eficácia da ideia em relação ao algoritmo de coloração sequencial sem a heurística. Faça experimentos com grafos não-dirigidos aleatórios.

Cliques

Uma clique num grafo não-dirigido é um conjunto de vértices adjacentes entre si. A figura mostra uma clique de tamanho 4. Encontre cliques de tamanho 5, 6 e 7 na figura.

É fácil encontrar uma clique pequena num grafo não-dirigido: cada vértice é uma clique de tamanho 1 e cada aresta corresponde a uma clique de tamanho 2. É bem mais difícil encontrar uma clique grande.

Há uma relação simples entre cliques e coloração de vértices: se um grafo não-dirigido tem uma clique de tamanho q, então qualquer coloração válida precisa de pelo menos q cores. Portanto, se um grafo não-dirigido tem uma clique de tamanho q e uma coloração válida com apenas q cores, a coloração é mínima e a clique é máxima. (Em geral, entretanto, uma clique máxima é bem menor que o número de cores de uma coloração válida mínima.)

Exemplo E. No grafo do Sudoku (veja o exemplo B), há cliques com 9 vértices e portanto toda coloração válida precisa de pelo menos 9 cores. Por outro lado, qualquer coloração que use apenas 9 cores prova que o grafo não tem cliques com mais que 9 vértices.

Exercícios 5

Escreva uma função que calcule uma clique maximal de um grafo não-dirigido G, ou seja, uma clique que não esteja contida em nenhuma clique maior.
Grafo da dama. O grafo da dama é definido da seguinte maneira. Os vértices são as casas do tabuleiro de xadrez e dois vértices são adjacentes se uma dama (em inglês, o nome da peça é queen) do jogo de xadrez pode saltar de um deles para o outro em um só movimento. Mais precisamente, duas casas são adjacentes se estiverem na mesma linha, na mesma coluna, na mesma diagonal ascendente, ou na mesma diagonal descendente. O tabuleiro de xadrez tradicional tem 8 linhas e 8 colunas, mas um grafo da dama generalizado pode ser definido sobre um tabuleiro com t linhas e t colunas, para qualquer t. Escreva uma função UGRAPHchessQueen() que construa o grafo da dama no tabuleiro t-por-t.
Dama do xadrez 3-por-3. Exiba uma clique máxima no grafo da dama no tabuleiro 3-por-3. Exiba uma coloração mínima do grafo. Prove que sua coloração é mínima.
Dama do xadrez t-por-t. Quantos são os vértices de uma clique máxima no grafo da dama num tabuleiro de xadrez t-por-t? Qual o número mínimo de cores necessário para uma coloração válida do grafo?
Dê um grafo não-dirigido em que uma clique máxima é bem menor que o número mínimo de cores de uma coloração válida.
Coloração versus pontes. Seja a uma ponte de um grafo não-dirigido G. Suponha que G−a tem uma coloração com k ≥ 2 cores. Mostre que G também tem uma coloração com k cores.
Coloração versus componentes aresta-biconexas. Suponha que cada componente aresta-biconexa de um grafo não-dirigido G tem uma coloração com k ≥ 2 cores. Mostre que G também tem uma coloração com k cores. (Dica: considere a floresta de componentes aresta-biconexas de G.)

Perguntas e respostas

Pergunta: Não seria melhor dizer simplesmente coloração, sem o adjetivo válida?
Resposta: Eu gostaria de fazer isso, mas ao discutir algumas heurísticas sou levado a examinar colorações provisórias inválidas, que atribuem a mesma cor a dois vértices adjacentes.
Pergunta: Não seria melhor dizer k-cromático em lugar de k-colorível?
Resposta: Não. Por definição, um grafo é k-cromático se for k-colorível mas não (k−1)-colorível.

Coloração de vértices