Grafos aresta-biconexos e pontes

Como sabemos, um grafo não-dirigido é conexo se cada dois de seus vértices são ligados por um caminho. Grafos não-dirigidos aresta-biconexos satisfazem uma condição mais forte: cada dois de seus vértices são ligados por dois caminhos sem arestas em comum. (A expressão sem arestas em comum significa que nenhuma aresta pertence a ambos os caminhos, ou seja, se um arco v-w pertence a um dos caminhos então nem v-w nem w-v pertence ao outro.) Essa definição é natural e intuitiva mas difícil de manejar. Por isso, adotaremos abaixo uma definição equivalente que é mais cômoda (ainda que não explique a expressão biconexo).

Este capítulo trata do problema de decidir se um dado grafo é aresta-biconexo. Em especial, discute um algoritmo eficiente para o problema.

Aresta-biconexão

Num grafo não-dirigido, qualquer aresta que não pertence a um circuito é conhecida como ponte (= bridge). Portanto, um grafo não-dirigido é aresta-biconexo se e somente se é conexo e não tem pontes.

Pontes podem ser caracterizadas pela seguinte propriedade: uma aresta a de um grafo não-dirigido conexo G é uma ponte se e somente se o grafo G−a é desconexo. (Nesse sentido, grafos sem pontes são tolerantes a falhas.)

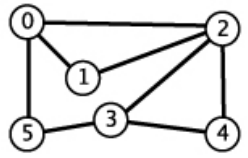
Exemplo A. O grafo da primeira figura é aresta-biconexo. O grafo da segunda figura não é aresta-biconexo pois, embora conexo, tem pontes. As pontes são 0-5, 6-7 e 11-12.

Exercícios 1

Mostre que o grafo 0-1 1-2 2-3 3-4 4-5 5-6 6-0 é aresta-biconexo.
O grafo não-dirigido definido pelo conjunto de arestas 0-1 1-2 2-0 1-3 3-4 4-1 3-5 5-4 é aresta-biconexo?
Mostre que todo grafo completo com 3 ou mais vértices é aresta-biconexo. Mostre que um grafo completo com apenas 2 vértices não é aresta-biconexo. Mostre que um grafo completo com apenas 1 vértice é aresta-biconexo.
Mostre que uma aresta a de um grafo não-dirigido G é uma ponte se e somente se o grafo G−a tem mais componentes conexas que G.
É verdade que toda grade não-dirigida m-por-n é aresta-biconexa?
★ Florestas. Mostre que um grafo não-dirigido é uma floresta se e somente se todas as suas arestas são pontes.
Ligação dupla versus circuito. Dizemos que dois vértices s e t de um grafo não-dirigido estão duplamente ligados se existem dois caminhos de s a t sem arestas em comum. Mostre que dois vértices distintos de um grafo não-dirigido estão duplamente ligados se e somente se os dois pertencem a um mesmo circuito (não necessariamente simples).
Aresta-biconexão versus ligação dupla. Mostre que um grafo é aresta-biconexo se e somente se cada dois de seus vértices estão duplamente ligados.

O problema

A habilidade de decidir rapidamente se um dado grafo é aresta-biconexo é muito útil. Esse é o problema algorítmico central do presente capítulo:

A parte mais interessante do problema é decidir se o grafo tem pontes. Para fazer isso, basta verificar se a remoção de alguma aresta desconecta o grafo. Mas a aplicação inocente dessa ideia resulta em um algoritmo muito ineficiente.

Robert Tarjan mostrou (1974) como a busca DFS pode ser usada para verificar, eficientemente, a existência de pontes. O algoritmo de Tarjan é o assunto principal deste capítulo. Para entender o algoritmo será necessário percorrer um caminho relativamente longo. Precisamos entender

Exercícios 2

Algoritmo ingênuo para aresta-biconexão. Implemente o seguinte algoritmo ingênuo para decidir se um grafo não-dirigido é aresta-biconexo. Primeiro, use a função UGRAPHcon() para decidir se o grafo é conexo. Depois, use a função GRAPHreach() para verificar se alguma aresta é ponte. (Cuidado: a implementação do algoritmo não é inteiramente trivial.) Quanto tempo esse algoritmo consome? Onde o algoritmo desperdiça tempo?

Pontes, florestas e abraços

É fácil perceber que toda floresta DFS de num grafo não-dirigido passa por todas as pontes do grafo. Mas é preciso formular essa propriedade com mais cuidado pois pontes são arestas enquanto florestas DFS são formadas por arcos:

Quais arcos da floresta DFS fazem parte de pontes? (Dizemos que um arco faz parte de uma ponte se for um dos dois arcos que constituem a ponte.) A seguinte definição dá um passo na direção da resposta. Dado um arco u-v da floresta DFS, dizemos que um arco x-y do grafo abraça u-v se as seguintes condições forem satisfeitas:

(Note que x pode ser igual a v e y pode ser igual a u.) É óbvio que qualquer arco que abraça u-v é um arco de retorno e portanto fecha um circuito que passa por u-v. A recíproca é verdadeira, embora não seja tão óbvia. Isso leva à seguinte caracterização:

A partir deste ponto, será mais cômodo associar a ideia de abraço à ponta final de cada arco da floresta DFS. Assim, diremos que um arco x-y do grafo abraça um vértice v se abraça o arco de floresta que entra em v. (É claro que isso só faz sentido se v não é uma raiz.) Em outras palavras, x-y abraça v se x é descendente de v na floresta, y é ancestral próprio de v na floresta, e x é diferente de v ou y é diferente do pai de v.

Exemplo B. Considere grafo definido pelas listas de adjacência abaixo. Veja a figura. Observe que as arestas 1-8, 8-10 e 4-9 são as únicas pontes do grafo.

Uma busca DFS produz a floresta DFS representada na figura à direita. Você deve imaginar que todos os arcos da figura estão dirigidos de cima para baixo na figura. Cada um dos demais arcos do grafo é de avanço ou de retorno em relação à floresta. (Acrescente esses arcos à figura.) Observe que a floresta contém um dos arcos de cada ponte. O arco 2-3 da floresta não faz parte de uma ponte porque é abraçado pelo arco 8-2. O arco 4-7 da floresta não faz parte de uma ponte porque é abraçado pelo arco 7-10. Já o arco 8-1 da floresta faz parte de uma ponte pois não é abraçado por nenhum arco do grafo. Da mesma forma, os arcos 8-10 e 4-9 da floresta fazem parte de pontes pois não são abraçados por arcos do grafo.

Exemplo C. Considere o grafo não-dirigido definido pelas listas de adjacência abaixo. Veja ao lado uma floresta DFS do grafo. Você deve imaginar que todos os arcos da figura estão dirigidos de cima para baixo e acrescentar à figura os demais arcos do grafo.

Como o grafo é não-dirigido, todos os arcos que não pertencem à floresta DFS ligam um ancestral a um descendente. O arco 5-3 abraça os vértices 5 e 4. O arco 6-1 abraça os vértices 6 e 2. Os demais arcos não abraçam vértice algum. Portanto, 2-3 e 0-1 são as únicas pontes.

Exercícios 3

Considere o grafo não-dirigido definido pelo conjunto de arestas 8-9 3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4. Faça uma busca DFS no grafo e desenhe uma figura da floresta DFS. Quais arcos da floresta DFS são abraçados por arcos do grafo? Quais arcos fazem parte de pontes?
Prove a propriedade DFS das pontes.
Prove o lema do abraço.
Aplique o lema do abraço a uma árvore.
Depois de uma busca DFS num grafo não-dirigido, seja u-v um arco da floresta DFS e seja x-y um arco do grafo. Suponha que pre[y] ≤ pre[u], pre[v] ≤ pre[x], e pelo menos uma dessas desigualdades é estrita. É verdade que x-y abraça u-v?
Algoritmo ingênuo. Faça uma busca DFS num grafo não-dirigido; marque todos os arcos da floresta DFS; para cada arco de retorno x-y que não seja antiparalelo a um arco da floresta, desmarque todos os arcos do caminho y-...-x na floresta. No fim, as arestas cujos arcos ainda estão marcados são as pontes do grafo. Quanto tempo esse algoritmo consome? Mostre um grafo não-dirigido para o qual o algoritmo é particularmente lento.

Número de pré-ordem mínimo

Para que o lema do abraço possa ser usado de maneira eficiente, é preciso introduzir um conceito auxiliar. Digamos que pre[] é a numeração em pré-ordem produzida pela busca DFS no grafo. Então o número de pré-ordem mínimo (= lowest preorder number) ao alcance de um vértice v é o número

sendo o mínimo tomado sobre todos os arcos x-y que abraçam v. (Muitos livros escrevem low[] no lugar do meu lo[].) De acordo com a definição, lo[v] é infinito se nenhum arco abraça v. Mas é mais conveniente dizer que lo[v] = pre[v] nesse caso. Essa definição faz sentido pois se algum arco abraça v então lo[v] < pre[v]. Graças a essa definição, podemos dizer que lo[v] ≤ pre[v] para todo vértice v sem exceção.

Combinado com o lema do abraço, o vetor lo[] permite dizer que um arco u-v da floresta DFS é uma ponte se e somente se

Exemplo D. Considere o grafo não-dirigido com vértices a b c d e f g h i j definido pelas listas de adjacência abaixo. Veja à direita a figura de uma floresta DFS do grafo. Você deve imaginar que todos os arcos estão dirigidos de cima para baixo na figura e acrescentar à figura as demais arestas do grafo. À esquerda de cada vértice v da figura aparece o número pre[v] e à direita o número lo[v].

O arco d-e da floresta faz parte de uma ponte porque lo[e] ≡ 4 ≡ pre[e]. O arco i-j da floresta faz parte de uma ponte porque lo[j] ≡ 9 ≡ pre[j]. As arestas d-e e i-j são as únicas pontes do grafo.

Cálculo eficiente de lo[ ]. Poderíamos calcular lo[v] diretamente a partir da definição, mas isso seria muito ineficiente. Um cálculo eficiente usa a seguinte fórmula recursiva, que exprime o valor que lo[] tem em v em função dos valores que lo[] tem nos filhos de v. Para cada vértice v, lo[v] é o menor dos seguintes números:

Essa fórmula vale porque qualquer arco x-y que abraça um filho w de v também abraça v, a menos que y seja igual a v. Para aplicar a fórmula, basta examinar os vértices de baixo para cima, começando com as folhas da floresta DFS e subindo em direção às raízes. Em outras palavras, basta examinar os vértices em pré-ordem inversa, pois nessa ordem todo vértice vem depois de seus filhos (já que a pré-ordem é uma permutação topológica dos vértices da floresta DFS). Na verdade, podemos igualmente bem examinar os vértices em pós-ordem, pois também nessa ordem todo vértice aparece depois de seus filhos. A função a seguir faz exatamente isso:

#define UGraph Graph
static int pre[1000];
static vertex pa[1000];
static int lo[1000];
#define min( A, B) (A) < (B) ? (A) : (B);

/* Esta função faz uma busca DFS no grafo não-dirigido G
e calcula o lowest preorder number lo[]
de cada vértice de G.
Também calcula os vetores pre[], post[] 
e pa[] correspondentes à busca DFS. */

void UGRAPHlo( UGraph G) 
{ 
   GRAPHdfs( G); // calcula pre[], post[] e pa[]
   vertex vv[1000];
   for (vertex v = 0; v < G->V; ++v)
      vv[post[v]] = v;
   // vv[0..V-1] é permutação em pós-ordem
   for (int i = 0; i < G->V; ++i) {
      vertex v = vv[i];
      lo[v] = pre[v];
      for (link a = G->adj[v]; a != NULL; a = a->next) {
         vertex w = a->w;
         if (pre[w] < pre[v]) { // A 
            if (w != pa[v]) 
               lo[v] = min( lo[v], pre[w]);
         } else { // B 
            if (pa[w] == v)
               lo[v] = min( lo[v], lo[w]);
         }
      }
   }
}

No ponto B, o vértice w é descendente próprio de v. Será filho de v se tivermos pa[w] ≡ v. Como w é descendente de v, o valor de lo[w] já está definido podendo ser usado na comparação com lo[v]. (A cláusula if (pa[w] == v) é redundante, pois se lo[w] < lo[v] então lo[w] ≡ pre[y] para algum arco x-y que abraça w e nesse caso x-y também abraça v.)

Exemplo E. Considere novamente o grafo não-dirigido do exemplo B. Para que o exemplo fique mais legível, usaremos os seguintes nomes alfabéticos alternativos para os vértices:

Veja à direita a figura de uma floresta DFS do grafo. Você deve imaginar que todos os arcos estão dirigidos de cima para baixo na figura. À esquerda de cada vértice v aparece o número pre[v] e à direita o número lo[v]. Veja os vetores pre[], post[] e lo[]:

Como os vértices estão listados em pós-ordem na primeira linha da tabela, é fácil aplicar a fórmula recursiva e assim verificar que a linha lo[] da tabela está correta. O arco e-j da floresta faz parte de uma ponte porque lo[j] ≡ 8 ≡ pre[j]. O arco i-k da floresta faz parte de uma ponte porque lo[k] ≡ 5 ≡ pre[k]. O arco i-b faz parte de uma ponte pois lo[b] ≡ 4 ≡ pre[b]. As arestas e-j, i-k e i-b são as únicas pontes do grafo.

Exercícios 4

Calcule lo[] para o grafo da figura.
Calcule lo[] para o grafo do exemplo C acima.
Faça uma busca DFS em uma árvore. Depois, calcule lo[] diretamente a partir da definição.
Considere o grafo-circuito 0-1-2-3-4-5-6-7-8-9-0. Faça uma busca DFS a partir do vértice 0. Calcule lo[] diretamente a partir da definição.
Considere o trevo de 3 folhas definido pelos arcos 0-1 1-0 1-2 2-1 1-3 3-2. Calcule a numeração lo[] diretamente a partir da definição.
Aplique a função UGRAPHlo() ao grafo não-dirigido definido pelas arestas 0-9 9-6 6-1 1-3 3-2 2-7 3-4 4-5 4-8 9-8 6-3 3-7. Examine os vértices em ordem crescente de nomes.

Critique a seguinte maneira de calcular o vetor lo[]. O código está correto? É eficiente?

void lowestPre( UGraph G) { 
   GRAPHdfs( G);
   for (vertex v = 0; v < G->V; ++v) lo[v] = pre[v];
   for (vertex v = 1; v < G->V; ++v) 
      for (link a = G->adj[v]; a != NULL; a = a->next) {
         vertex w = a->w;
         if (pre[w] < pre[v] && w != pa[v]) { 
            vertex x = v;
            while (lo[x] > pre[w]) {
               lo[x] = pre[w];
               x = pa[x]; } } } }

Faça uma busca DFS a partir do vértice 0 num grafo não-dirigido aresta-biconexo. Mostre que lo[0] ≡ pre[0] e lo[v] < pre[v] para cada vértice v diferente de 0.
★ Mostre, diretamente a partir da definição de lo[], que lo[v] ≤ lo[w] para qualquer vértice v e qualquer filho w de v.
Prova da fórmula. Prove a fórmula recursiva para lo[].
★ Versão recursiva de UGRAPHlo(). Escreva uma versão recursiva da função UGRAPHlo(). (Comece com os códigos de GRAPHdfs() e dfsR(). Depois, acrescente linhas de código apropriadas para calcular lo[].) Aplique a função que você acabou de escrever ao grafo definido pelas listas de adjacência abaixo e faça o rastreamento da execução da função. Nas linhas do rastreamento que representam o fim do processamento de um vértice v, anote o valor de lo[v]. (Esse rastreamento mostra como pre[] é calculado de cima para baixo na floresta DFS enquanto lo[] é calculado de baixo para cima.) [Solução]
```
a: b
b: c a f
c: d b
d: e c
e: f d
f: b e
```
★ Lista de pontes. Escreva uma função que imprima uma lista de todas as pontes de um grafo não-dirigido depois de invocar UGRAPHlo().

Algoritmo de Tarjan para aresta-biconexão

Finalmente, podemos apresentar o algoritmo de Tarjan (não confunda com Tarzan [smile]

) para o problema da aresta-biconexão. Depois de usar a função UGRAPHlo() para calcular os vetores pre[] e lo[], o algoritmo verifica a existência de pontes aplicando o teste lo[v] ≡ pre[v] a todo vértice v.

#define UGraph Graph
static int pre[1000], post[1000];
static vertex pa[1000];
static int lo[1000];

/* A função UGRAPHebicon3() decide se 
   o grafo não-dirigido G
   é aresta-biconexo.
   (A função implementa o algoritmo de Tarjan.) */

bool UGRAPHebicon3( UGraph G) 
{ 
   UGRAPHlo( G); // calcula pre[], pa[] e lo[]
   for (vertex v = 0; v < G->V; ++v) {
      if (lo[v] == pre[v] && pa[v] != v)
         return false; // pa[v]-v é ponte
   }
   int roots = 0;
   for (vertex v = 0; v < G->V; ++v) {
      if (pa[v] == v) ++roots;
      if (roots > 1) 
         return false; // G é desconexo
   }
   return true;
}

Desempenho. Como acontece com muitos algoritmos baseados na busca em profundidade, a função UGRAPHebicon3() consome apenas V + E unidades de tempo quando aplicada a um grafo com V vértices e E arestas. Podemos dizer, portanto, que a função é linear. A variante de UGRAPHebicon3() para matrizes de adjacência consome tempo proporcional a V²; esse desempenho é linear no caso de grafos densos.

Exercícios 5

Aplique a função UGRAPHebicon3() ao grafo não-dirigido que tem vértices a b ... j e as seguintes listas de adjacência:
```
a: b
b: e c a
c: j e d b
d: e c
e: h g f d c b
f: e g
g: f e
h: j i e
i: h
j: c h
```
Aplique a função UGRAPHebicon3() ao grafo não-dirigido definido pelas arestas 0-1 1-2 2-3 3-4 4-5 4-6 6-7 7-1.
[Sedgewick figura 18.17] Aplique a função UGRAPHebicon3() ao grafo da figura. Faça uma figura da floresta DFS do grafo.

Implementação on-the-fly do algoritmo de Tarjan

Ao invocar UGRAPHlo(), a função UGRAPHebicon3() examina o grafo todo duas vezes. Embora isso resulte em um algoritmo linear, é preferível obter o mesmo efeito examinando o grafo uma só vez. Para isso, é preciso detectar a presença de pontes durante a execução de uma busca em profundidade e interromper a busca assim que uma ponte for encontrada. (Para melhor entender como isso pode ser feito, é uma boa ideia escrever antes uma versão recursiva de UGRAPHlo().)

#define UGraph Graph
static int cnt, pre[1000];
static vertex pa[1000];
static int lo[1000];
#define min( A, B) (A) < (B) ? (A) : (B)

/* A função UGRAPHebicon() decide se o grafo não-dirigido G
   é aresta-biconexo.
   (Esta é uma implementação on-the-fly do algoritmo de Tarjan.
   Código inspirado no programa 18.7 
   de Sedgewick.) */

bool UGRAPHebicon( UGraph G) 
{ 
   for (vertex v = 0; v < G->V; ++v)
      pre[v] = -1;
   cnt = 0;
   pa[0] = 0;
   if (dfsRbridge( G, 0)) // G tem ponte
      return false;
   for (vertex v = 1; v < G->V; ++v)
      if (pre[v] == -1) // G é desconexo 
         return false;
   return true;
}

/* A função dfsRbridge() calcula lo[v]. 
   Devolve true se houver uma ponte 
   na subfloresta DFS que tem raiz v.

   Senão, devolve false. */

static bool dfsRbridge( UGraph G, vertex v)
{ 
   pre[v] = cnt++;
   lo[v] = pre[v];
   for (link a = G->adj[v]; a != NULL; a = a->next) {
      vertex w = a->w;
      if (pre[w] != -1) { // v-w é de retorno ou avanço
         if (w != pa[v]) // A
            lo[v] = min( lo[v], pre[w]); // B
      } else {
         pa[w] = v;
         if (dfsRbridge( G, w)) // calcula lo[w]
            return true; // C 
         if (lo[w] == pre[w]) // v-w é ponte
            return true; // D 
         lo[v] = min( lo[v], lo[w]); // E 
      }
   }
   return false; // F 
}

Assim como UGRAPHlo(), a função dfsRbridge() calcula o vetor lo[] de baixo para cima, ou seja, começando pelas folhas da floresta DFS (linhas A e B) e subindo em direção às raízes da floresta. O valor de lo[w] calculado na linha calcula lo[w] é passado para cima na linha E, onde pode contribuir para o valor de lo[v]. A linha D interrompe a execução de dfsRbridge() quando a primeira ponte é encontrada.

Desempenho. Como acontece com muitos algoritmos baseados em busca em profundidade, esta versão on-the-fly da função UGRAPHebicon() consome apenas V + E unidades de tempo quando aplicada a um grafo não-dirigido com V vértices e E arestas. Podemos dizer, portanto, que a função é linear. A variante de UGRAPHebicon() para matrizes de adjacência consome tempo proporcional a V²; esse desempenho é linear no caso de grafos densos.

A encarnação dfsRbridge(G,1) de dfsRbridge() devolve false na linha F da função e morre. Depois disso, a encarnação dfsRbridge(G,8) descobre a ponte 8-1 na linha D, devolve true, e morre. Em seguida, a encarnação dfsRbridge(G,3) devolve true na linha C e morre. E assim por diante. Veja o estado final dos vetores pre[] e lo[]:

Exemplo G. Aplique a função UGRAPHebicon() ao grafo-circuito definido pelas listas de adjacência a seguir. (A figura mostra a floresta DFS construída por UGRAPHebicon().)

A função UGRAPHebicon() devolve true. Veja o estado final dos vetores pre[] e lo[]:

Exercícios 6

Aplique a função UGRAPHebicon() a uma floresta. Explique o que acontece em cada linha do código da função.
Aplique a função UGRAPHebicon() ao grafo-circuito 0-1-2-3-4-5-6-7-8-9-0. Explique o que acontece em cada linha do código da função.
★ Testes de depuração/validação. Escreva um programa para testar as funções UGRAPHebicon3() e UGRAPHebicon(). Seu programa deve comparar o resultado (true ou false) dessas funções com o de algum algoritmo ingênuo, como o sugerido num dos exercícios acima. Use grafos não-dirigidos conexos aleatórios com V vértices e E arestas para fazer os testes; o usuário deve fornecer os valores V e E pela linha de comando. Use grades m-por-n para fazer mais testes; o usuário deve fornecer os valores m e n pela linha de comando. Aproveite para comparar o consumo de tempo das três funções.
★ Atualize sua biblioteca. Acrescente a função UGRAPHebicon() à biblioteca GRAPHlists mencionada no capítulo Estruturas de dados para grafos. Aloque os vetores pre[], pa[] e lo[] dinamicamente. Repita o exercício para a biblioteca GRAPHmatrix.
★ Número de pontes. Escreva uma variante da função UGRAPHebicon() que calcule o número de pontes de um grafo não-dirigido. Escreva uma função enxuta, sem comandos nem variáveis supérfluos. Aplique a função ao grafo do exemplo B. Importante: faça um rastreamento da execução da função.

Perguntas e respostas

Pergunta: Não seria mais fácil dizer grafo biconexo no lugar do trava-língua grafo aresta-biconexo?
Resposta: Infelizmente, a tradição já reservou o adjetivo biconexo para um conceito diferente.
Pergunta: Não seria mais simples restringir a atenção a grafos não-dirigidos conexos ao tratar do problema das pontes?
Resposta: Não. A restrição a grafos conexos não simplifica nada.