Como saber se um vértice de um grafo é acessível a partir de outro?

Como descobrir, algoritmicamente, se é possível ir de um dado vértice de um grafo a um outro viajando pelos arcos? A solução discutida neste capítulo constitui um primeiro contato com o método de busca em profundidade. Esse primeiro contato é importante porque mostra o método na sua forma mais despojada.

Problema básico

Dizemos que um vértice t de um grafo está ao alcance de (ou é acessível a partir de) um vértice s se existe um caminho de s a t no grafo. (É apropriado lembrar que a existência de um caminho é equivalente à existência de um caminho simples.) Esse conceito leva imediatamente ao seguinte

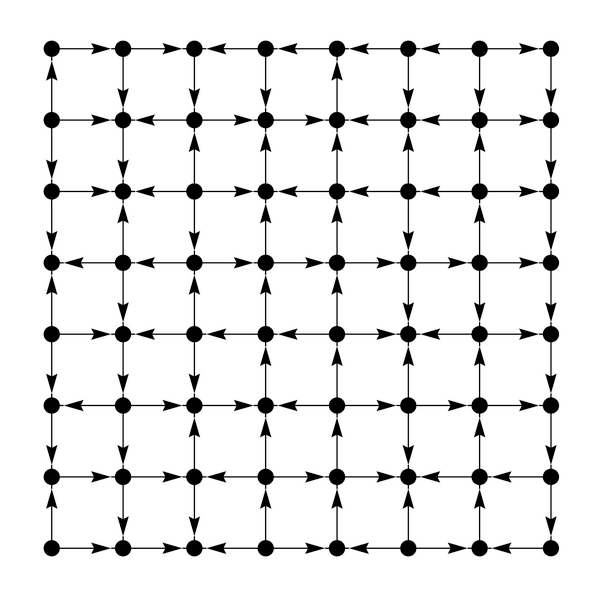
Um exemplo: no grafo da figura, queremos saber se o vértice no extremo sudeste está ao alcance do vértice no extremo noroeste.

Não vamos insistir, por enquanto, em obter um caminho explícito de s a t; queremos apenas saber se um tal caminho existe.

Uma solução

A função GRAPHreach() abaixo usa o clássico método de exploração de labirintos para descobrir se t está ao alcance de s e assim resolver o problema. A função faz uma numeração dos vértices usando os rótulos 0 e 1: um vértice recebe rótulo 1 se está ao alcance de s e recebe rótulo 0 em caso contrário. Os rótulos são armazenados num vetor visited[0..V-1] indexado pelos vértices. Diremos que um vértice v já foi visitado se visited[v] vale 1. Assim, visitar um vértice pela primeira vez é atribuir 1 a visited[v].

/* Para simplificar, 
   suporemos que nossos grafos têm no máximo 1000 vértices
   e trataremos o vetor visited[] como variável global. */

static int visited[1000];

  /* A função GRAPHreach() recebe vértices s 
   e t de um grafo G e
   decide se t está ao alcance de s
   ou não. */

bool GRAPHreach( Graph G, vertex s, vertex t) 
{ 
   for (vertex v = 0; v < G->V; ++v)
      visited[v] = 0;
   reachR( G, s);
   if (visited[t] == 0) return false;
   else return true;
}

A função GRAPHreach() é apenas um invólucro. O trabalho todo é realizado pela função recursiva reachR():

Para explicar o que a função reachR() faz, é preciso entender o ambiente em que cada execução da função começa. Imediatamente antes de cada invocação da função, temos um certo conjunto de vértices já visitados. Ao receber argumentos G e v, e tendo por ambiente um conjunto X de vértices x tais que visited[x] vale 1, a função visita todos os vértices de todos os caminhos em G que começam em v e não passam por vértices de X.

Embora o problema básico trate apenas da acessibilidade de t, a função GRAPHreach() produz informações suficientes para decidir a acessibilidade de todos os vértices do grafo. Poderíamos interromper a execução da função tão logo fique claro que t está ao alcance de s; isso produziria uma versão ansiosa da função. Mas um dos exercícios abaixo mostra que não vale a pena fazer isso.

Exemplo A. Seja G o grafo com vértices 0 1 2 3 4 9 e arcos 0-1 0-6 1-2 1-3 1-5 3-4 6-7 6-9 7-8. Veja a matriz de adjacências de G (com - representando 0):

Para decidir se o vértice 8 está ao alcance do vértice 0, invocamos a função GRAPHreach() com argumentos (G,0,8). (Nesse exemplo, G é uma árvore radicada. Portanto, a resposta será afirmativa se e somente se 8 for um descendente de 0.)

A seguinte tabela é o rastro da execução da função reachR(). Cada linha da tabela registra o momento em que um arco é percorrido, ou seja, o momento em que reachR() se depara com um arco v-w ao examinar os vizinhos de v. Em seguida, a linha da tabela registra a correspondente invocação de reachR(). A execução de cada nova instância de reachR() é indicada por uma indentação apropriada da linha. Na coluna direita da tabela, cada linha exibe o estado do vetor visited[] (com - no lugar de 0) imediatamente depois que v é visitado pela primeira vez na correspondente invocação de reachR():

O estado final do vetor visited[] mostra que 8 está ao alcance de 0 no grafo.

Exemplo B. Seja G o grafo com vértices 0 1 2 3 4 9 e arcos 0-1 0-2 1-3 1-4 2-5 2-6 2-7 4-8 6-9. Esse grafo difere do anterior apenas nos nomes dos vértices, mas isso afeta o andamento da função GRAPHreach(). Veja a matriz de adjacências de G (com - representando 0):

Para decidir se o vértice 8 está ao alcance do vértice 0, invocamos a função GRAPHreach() com argumentos (G,0,8). Cada linha da seguinte tabela registra o momento em que um arco é percorrido. Em seguida, registra a correspondente invocação de reachR(). Na coluna direita da tabela, cada linha exibe o estado do vetor visited[] imediatamente depois que v é visitado pela primeira vez na correspondente invocação de reachR():

O estado final do vetor visited[] mostra que 8 está ao alcance de 0 no grafo. (Todos os outros vértices também estão ao alcance de 0.)

Exemplo C. Seja G o grafo com vértices 0 1 2 3 4 5 e arcos 0-2 0-3 0-4 2-1 2-4 3-4 3-5 4-1 4-5 5-1. Veja o vetor de listas de adjacência de G:

Para decidir se o vértice 5 está ao alcance do vértice 0, invocamos a função GRAPHreach() com argumentos (G,0,5). Cada linha da seguinte tabela registra o momento em que um arco é percorrido. Em seguida, registra a correspondente invocação de reachR():

O estado final do vetor visited[] mostra que todos os vértices estão ao alcance de 0.

Exemplo D. Considere novamente o grafo G do exemplo anterior. Veja, mais uma vez, as listas de adjacência de G:

Desta vez, queremos decidir se 3 está ao alcance de 2. Segue o rastro da execução de reachR() com argumentos (G,2,3):

O estado final do vetor visited[] mostra que 3 não está ao alcance de 2. (O vértice 0 também não está ao alcance de 2.)

Cabe levantar a seguinte dúvida a respeito desse exemplo D: o resultado poderia ser diferente se os vizinhos de cada vértice fossem examinados em alguma outra ordem? Para provar que a resposta é negativa, observe que nenhum arco sai do conjunto de vértices 1 2 4 5 e portanto nenhum caminho pode começar em 2 e terminar fora do conjunto. Isso prova que, de fato, 3 não está ao alcance de 2.

Exercícios 1

★ Instâncias extremas. A função GRAPHreach() funciona corretamente quando s é igual a t? E quando G->A vale 0? E quando G->V vale 1?
★ Documentação de reachR(). Escreva uma documentação correta da função recursiva reachR(), ou seja, diga o que a função faz. (Como acontece com muitas funções recursivas, não é fácil escrever uma documentação precisa.) [Solução]
Permutação dos vizinhos. Refaça o rastreamento (= trace) dos exemplos A e B acima depois de trocar for (w = 0; w < G->V; ++w) por for (w = G->V-1; w >= 0; --w) no código da versão de reachR() para matriz de adjacências.
Permutação dos vizinhos. Refaça o rastreamento dos exemplos A e B acima depois de alterar o código da versão de reachR() para matriz de adjacências de modo que os vértices sejam examinados na ordem z z+1 ... V-1 0 1 ... z-1 para algum valor de z.
Permutação dos vizinhos. Refaça o rastreamento dos exemplos C e D acima supondo que o grafo G é representado pelas seguintes listas de adjacência:
```
0: 2 3 4
1:      
2: 1 4  
3: 4 5  
4: 1 5  
5: 1    
```
Faça o rastreamento da execução de GRAPHreach(G,2,6) para o grafo não-dirigido G definido pelo conjunto de arestas 0-6 0-1 0-2 0-5 4-3 5-3 5-4 6-4 7-8 9-12 9-10 9-11 11-12. Comece por escrever um vetor de listas de adjacência do grafo.
No grafo não-dirigido da figura, os vértices assinalados estão ao alcance um do outro?
Labirinto. Considere o labirinto da figura. Você sai do ponto central e quer alcançar a saída que está no canto inferior esquerdo. A figura mostra o resultado de um aplicação da função GRAPHreach(). As bolas coloridas indicam os pontos do labirinto que foram visitados. As bolas de cor cinza indicam os pontos a partir dos quais a exploração revelou um beco sem saída (ou seja, a partir das quais todos os pontos que podem ser alcançadas já foram alcançadas). Você deve verificar, passo a passo, se GRAPHreach() foi aplicada corretamente. (Veja vídeo no YouTube.)

Certificado de resposta negativa

No caso de resposta negativa, seria interessante fornecer um prova de que não existe caminho de s a t. Uma tal prova é muito simples: um conjunto S de vértices que contém s, não contém t, e tem a seguinte propriedade: nenhum arco sai de S.

O vetor visited[] na função GRAPHreach() é o vetor característico de um tal conjunto S.

Exercícios 2

★ Versão ansiosa da função. Escreva uma variante da função GRAPHreach() que pare imediatamente (e devolva true) ao descobrir que t está ao alcance de s. (O código de reachR() para essa variante é mais complicado que o da versão preguiçosa discutida acima.) Para tornar o exercício mais interessante, imprima um caminho de s a t antes de devolver true.
★ Versão para grafos não-dirigidos? Escreva uma função que decida se um vértice t está ao alcance de um vértice s em um grafo não-dirigido dado. Seu código tira proveito do caráter não-dirigido do grafo? O código é diferente de GRAPHreach()?
Versão iterativa. Escreva uma versão não recursiva de GRAPHreach().

Exercícios 3

Testes. Escreva um pequeno programa que teste a função GRAPHreach(). Invente testes interessantes. Para conferir uma resposta negativa, verifique se algum arco sai de um vértice visitado e entra em um não visitado. Use as funções de construção de grafos sugeridas nos exercícios do capítulo Estruturas de dados para grafos. Use as funções de construção de grafos sugeridas nos exercícios do capítulo Grafos topológicos.
[Sedgewick 17.90] Probabilidade de resposta afirmativa. Determine experimentalmente a probabilidade de que dois vértices escolhidos aleatoriamente estejam ao alcance um do outro num grafo não-dirigido aleatório com V vértices e número esperado E de arestas. Faça experimentos com diversos valores de V. Para cada V, tente determinar o valor de E a partir do qual a probabilidade de que dois vértices aleatórios estão ao alcance um do outro torna-se muito alta.
Vértice central e vértice popular. Esboce um algoritmo que decida se um dado grafo G tem um vértice r com a seguinte propriedade: todos os vértices de G estão ao alcance de r. Esboce um algoritmo que decida se um grafo G tem um vértice que esteja ao alcance de todos os outros.

Perguntas e respostas

Pergunta: Na documentação das funções, acho que deveríamos embrulhar as variáveis em aspas. Por exemplo, acho que deveríamos escrever A função recebe vértices 's' e 't' de um grafo 'G'.
Resposta: Nããão! Afinal, você não escreve Hoje encontrei 'Paulo' na faculdade.
Pergunta: No código de GRAPHreach(), o vetor auxiliar visited[] foi alocado estaticamente (ou seja, durante a compilação do código). Acho que o vetor deveria ter sido alocado dinamicamente (ou seja, durante a execução do programa), usando malloc().
Resposta: Concordo; eu deveria ter usado alocação dinâmica. Não fiz isso porque a alocação e posterior desalocação do vetor ocuparia várias linhas de código e desviaria a atenção do leitor para questões que não têm relação com a lógica do algoritmo.