Estruturas de dados para representação de grafos

Como representar um grafo de modo que ele possa ser processado eficientemente por um computador? Como fazer isso na linguagem C?

Introdução

Os vértices de nossos grafos serão representados por números inteiros. O conjunto de vértices será 0 1 2 ... V-1 . Poderíamos usar o tipo-de-dados int para representar vértices, mas é melhor ter um nome específico para esse tipo:

O conjunto de arcos de um grafo pode ser representado de várias maneiras. Discutimos abaixo duas representações clássicas:

Cada uma das representações tem suas vantagens e suas desvantagens. As descrições a seguir devem ser entendidas apenas como modelos e não como algo definitivo. As estruturas de dados serão modificadas e adaptadas mais adiante, conforme as necessidades.

Matriz de adjacências

A matriz de adjacências de um grafo é uma matriz booleana com colunas e linhas indexadas pelos vértices. Se adj[][] é uma tal matriz então, para cada vértice v e cada vértice w,

Assim, a linha v da matriz adj[][] representa o leque de saída do vértice v e a coluna w da matriz representa o leque de entrada do vértice w. Por exemplo, veja a matriz de adjacências do grafo cujos arcos são 0-1 0-5 1-0 1-5 2-4 3-1 5-3 :

Como nossos grafos não têm laços, os elementos da diagonal da matriz de adjacências são iguais a 0. Se o grafo for não-dirigido, a matriz é simétrica: adj[v][w] ≡ adj[w][v].

Um grafo é representado por uma struct graph que contém a matriz de adjacências, o número de vértices, e o número de arcos do grafo:

/* REPRESENTAÇÃO POR MATRIZ DE ADJACÊNCIAS: 
   A estrutura graph representa um grafo.
   O campo adj é um 
   ponteiro para 
   a matriz de adjacências do grafo.
   O campo V contém o número de vértices e 
   o campo A contém 
   o número de arcos do grafo. */

struct graph {
   int V; 
   int A; 
   int **adj; 
};

/* Um Graph é um ponteiro para um graph,
   ou seja, um Graph contém o 
   endereço de 
   um graph. */

typedef struct graph *Graph;

Seguem algumas ferramentas básicas para a construção e manipulação de grafos:

/* REPRESENTAÇÃO POR MATRIZ DE ADJACÊNCIAS: 
   A função GRAPHinit() constrói um grafo
   com vértices 0 1 .. V-1 e nenhum arco. */

Graph GRAPHinit( int V) { 
   Graph G = malloc( sizeof *G);
   G->V = V; 
   G->A = 0;
   G->adj = MATRIXint( V, V, 0);
   return G;
}

/* REPRESENTAÇÃO POR MATRIZ DE ADJACÊNCIAS: 
   A função MATRIXint() 
   aloca uma matriz com linhas 
   0..r-1 
   e colunas 0..c-1.
   Cada elemento da matriz recebe valor val. */

static int **MATRIXint( int r, int c, int val) { 
   int **m = malloc( r * sizeof (int *));
   for (vertex i = 0; i < r; ++i) 
      m[i] = malloc( c * sizeof (int));
   for (vertex i = 0; i < r; ++i)
      for (vertex j = 0; j < c; ++j)
         m[i][j] = val;
   return m;
}

/* REPRESENTAÇÃO POR MATRIZ DE ADJACÊNCIAS: 
   A função GRAPHinsertArc() 
   insere um arco v-w no grafo G.  
   A função supõe que v e w são distintos,
   positivos
   e menores que G->V.
   Se o grafo já tem um arco v-w, 
   a função não faz nada. */

void GRAPHinsertArc( Graph G, vertex v, vertex w) { 
   if (G->adj[v][w] == 0) {
      G->adj[v][w] = 1; 
      G->A++;
   }
}

/* REPRESENTAÇÃO POR MATRIZ DE ADJACÊNCIAS: 
   A função GRAPHremoveArc() 
   remove do grafo G
   o arco v-w.
   A função supõe que v e w são distintos,
   positivos e menores que G->V.
   Se não existe arco v-w, a função não faz nada. */

void GRAPHremoveArc( Graph G, vertex v, vertex w) { 
   if (G->adj[v][w] == 1) {
      G->adj[v][w] = 0; 
      G->A--;
   }
}

/* REPRESENTAÇÃO POR MATRIZ DE ADJACÊNCIAS: 
   A função GRAPHshow() imprime,
   para cada vértice v 
   do grafo G,
   em uma linha, 
   todos os vértices adjacentes a v. */

void GRAPHshow( Graph G) { 
   for (vertex v = 0; v < G->V; ++v) {
      printf( "%2d:", v);
      for (vertex w = 0; w < G->V; ++w)
         if (G->adj[v][w] == 1) 
            printf( " %2d", w);
      printf( "\n");
   }
}

O espaço ocupado por uma matriz de adjacências é proporcional a V², sendo V o número de vértices do grafo. No caso de grafos densos, esse espaço é proporcional ao tamanho do grafo. Para grafos esparsos, existem representações mais compactas, como veremos a seguir.

Listas de adjacência

O vetor de listas de adjacência de um grafo tem uma lista encadeada (= linked list) associada com cada vértice do grafo. A lista associada com um vértice v contém todos os vizinhos de v. Portanto, a lista do vértice v representa o leque de saída de v. Por exemplo, eis o vetor de listas de adjacência do grafo cujos arcos são 0-1 0-5 1-0 1-5 2-4 3-1 5-3 :

Na representação por listas de adjacência, um grafo é representado por uma struct graph que contém o vetor de listas de adjacência, o número de vértices, e o número de arcos do grafo:

/* REPRESENTAÇÃO POR LISTAS DE ADJACÊNCIA: 
   A estrutura graph representa um grafo.
   O campo adj 
   é um ponteiro para o vetor de listas de adjacência,
   o campo V contém o número de vértices
   e o campo A contém o número de arcos do grafo. */

struct graph {
   int V; 
   int A; 
   link *adj; 
};

/* Um Graph é um ponteiro para um graph. */

typedef struct graph *Graph;

/* A lista de adjacência de um vértice v
   é composta por nós do tipo node. 
   Cada nó da lista corresponde a um arco
   e contém um vizinho w
   de v e o endereço do nó seguinte da lista.
   Um link é um ponteiro para um node. */

typedef struct node *link;
struct node { 
   vertex w; 
   link next; 
};

/* A função NEWnode()  recebe um vértice w 
   e o endereço next de um nó
   e devolve o endereço a de um novo nó 
   tal que a->w == w
   e a->next == next. */

static link NEWnode( vertex w, link next) { 
   link a = malloc( sizeof (struct node));
   a->w = w; 
   a->next = next;     
   return a;                         
}

Eis algumas funções básicas de construção e manipulação de grafos representados por listas de adjacência:

/* REPRESENTAÇÃO POR LISTAS DE ADJACÊNCIA: 
   A função GRAPHinit() constrói um grafo
   com vértices 0 1 .. V-1 e nenhum arco. */

Graph GRAPHinit( int V) { 
   Graph G = malloc( sizeof *G);
   G->V = V; 
   G->A = 0;
   G->adj = malloc( V * sizeof (link));
   for (vertex v = 0; v < V; ++v) 
      G->adj[v] = NULL;
   return G;
}

/* REPRESENTAÇÃO POR LISTAS DE ADJACÊNCIA: 
   A função GRAPHinsertArc() 
   insere um arco v-w 
   no grafo G.  
   A função supõe que v e w são distintos,
   positivos
   e menores que G->V.
   Se o grafo já tem um arco v-w, 
   a função não faz nada. */

void GRAPHinsertArc( Graph G, vertex v, vertex w) { 
   for (link a = G->adj[v]; a != NULL; a = a->next) 
      if (a->w == w) return;
   G->adj[v] = NEWnode( w, G->adj[v]);
   G->A++;
}

A função GRAPHinsertArc() consome muito tempo (no pior caso, tempo proporcional ao número de arcos), pois verifica se o arco a inserir já existe no grafo.

O espaço ocupado pelo vetor de listas de adjacência é proporcional ao número de vértices e arcos do grafo, ou seja, proporcional ao tamanho do grafo. Portanto, listas de adjacência são uma maneira econômica de representação. Para grafos esparsos, listas de adjacência ocupam menos espaço que uma matriz de adjacências.

Exercícios 1

Resolva os exercícios abaixo para cada uma das estruturas de dados (matriz de adjacências e listas de adjacência) descritas acima.

Fontes e sorvedouros. Calcule um vetor booleano isSink[], indexado pelos vértices, que identifique os sorvedouros de um grafo. Repita com fontes no lugar se sourvedouros.
Considere o problema de decidir se um vértice v é isolado num grafo G. Quanto tempo a solução do problema consome? Dê sua resposta em função do número de vértices do grafo.
★ [Sedgewick 17.40] Escreva uma função GRAPHindeg() que calcule o grau de entrada de um vértice v de um grafo G. Escreva uma função GRAPHoutdeg() que calcule o grau de saída de v.
Escreva uma função GRAPHindegs() que receba um grafo G e um vetor indeg[] e preencha o vetor de modo que indeg[v] seja o grau de entrada do vértice v. Repita o exercício para graus de saída no lugar dos graus de entrada.
Considere o problema de decidir se dois vértices são adjacentes num grafo G. Quanto tempo consome a solução do problema? Dê sua resposta em função do número de vértices e arcos do grafo.
[Sedgewick 17.24, 17.29] Escreva uma função GRAPHdestroy() que destrua a representação de um grafo G, liberando o espaço que a representação ocupa na memória.
Teste de igualdade. Escreva uma função GRAPHequal() que decida se dois grafos, digamos G e H, são iguais.

Faça uma boa figura do grafo definido pelas seguintes listas de adjacência:

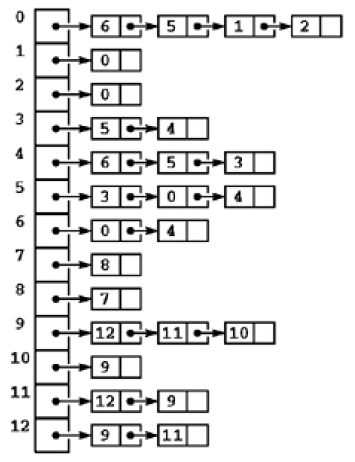
 0:  1  4
 1:  0  2  5
 2:  1  3  6
 3:  2  7
 4:  0  5  8
 5:  1  4  6  9
 6:  2  5  7 10
 7:  3  6 11
 8:  4  9
 9:  5  8 10
10:  6  9 11
11:  7 10

Transformação de uma representação em outra. Escreva funções que convertam uma representação de um grafo em outra. Por exemplo, convertam uma representação por matriz de adjacências na representação por listas de adjacência.
★ Alteração dos nomes dos vértices. Escreva uma função GRAPHrenameVertices() que receba um grafo G e uma permutação newname[] dos vértices de G (o vetor newname[] é indexado pelos vértices e tem valores em 0 1 2 ... V-1) e construa um grafo H isomorfo a G tal que o vértice v de G tenha como imagem o vértice newname[v] de H.

Exercícios 2: listas de adjacência

A representação de grafos por listas de adjacência merece alguns exercícios adicionais.

[Sedgewick 17.27] Escreva uma versão da função GRAPHshow() para grafos representados por listas de adjacência.
Remoção de arco. Escreva uma função GRAPHremoveArc() que receba dois vértices v e w de um grafo G representado por listas de adjacência e remova o arco v-w de G.
Faça uma figura do grafo representado pelas listas de adjacência da figura acima.
★ [Sedgewick 17.26] Considere o grafo definido pelos arcos abaixo. Faça uma figura do vetor de listas de adjacência quando os arcos são inseridas por GRAPHinsertArc(), na ordem dada abaixo, em um grafo inicialmente vazio.
```
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4
```
[Sedgewick 17.30] Dê um exemplo simples de um vetor de listas de adjacência que não pode ser gerado, a partir do grafo vazio, pela aplicação da função GRAPHinsertArc().
[Sedgewick Prog 19.1] Escreva uma função que receba um grafo e inverta todas as suas listas de adjacência. Por exemplo, se os 4 vizinhos de um certo vértice u aparecem na lista adj[u] na ordem v, w, x, y, então depois da aplicação da função a lista deve conter os mesmos vértices na ordem y, x, w, v.

Exercícios 3: grafos não-dirigidos

Os exercícios desta seção envolvem grafos não-dirigidos. Num grafo não-dirigido, cada par de arcos antiparalelos é uma aresta. Resolva os exercícios abaixo para cada uma das estruturas de dados (matriz de adjacências e listas de adjacência) descritas acima.

Não-dirigido? Escreva uma função GRAPHundir() que decida se um dado grafo é não-dirigido.
Inserção de aresta. Escreva uma função UGRAPHinsertEdge() que insira uma aresta v-w em um grafo não-dirigido G.
[Sedgewick 17.28] Remoção de aresta. Escreva uma função UGRAPHremoveEdge() que remova de um grafo não-dirigido G uma dada aresta v-w.
Graus. Escreva uma função UGRAPHdegrees() que receba um grafo não-dirigido e devolva um vetor g[], indexado por vértices, tal que g[v] é o grau do vértice v.
Ordem crescente de graus. Escreva uma função que receba um grafo não-dirigido G e calcule uma permutação vv[0..V-1] dos vértices que esteja em ordem crescente de graus.

Exercícios 4: construtores de grafos

Resolva cada exercício duas vezes: uma vez usando a representação por matriz de adjacências e outra vez usando a representação por listas de adjacência. (É apropriado rever o exercício Alteração dos nomes de vértices.)

Grafo completo. Escreva uma função que construa um grafo completo com V vértices. Procure escrever uma função limpa e eficiente.
Grade dirigida. A grade dirigida m-por-n tem vértices 0 1 2 ... m*n-1 distribuídos por m linhas e n colunas e tem arcos que vão de cada vértice ao vértice seguinte na mesma linha e ao vértice seguinte na mesma coluna. A grade 3-por-3, por exemplo, tem conjunto de arcos 0-1 1-2 3-4 4-5 6-7 7-8 0-3 3-6 1-4 4-7 2-5 5-8. Escreva uma função GRAPHrandDiGrid() que construa a grade dirigida m-por-n. Use uma permutação aleatória de 0..V-1 para dar nomes aos vértices.
Grafo não-dirigido completo. Um grafo não-dirigido é completo se todo par não-ordenado de vértices distintos é uma aresta. É claro que um grafo não-dirigido completo é exatamente o mesmo que um grafo completo. Escreva uma função UGRAPHbuildComplete() que construa um grafo não-dirigido completo com V vértices.
★ Grade não-dirigida.

A grade não-dirigida m-por-n tem vértices 0 1 2 ... m*n-1 distribuídos por m linhas e n colunas e tem arestas que ligam cada vértice ao vértice seguinte na mesma linha e ao vértice seguinte na mesma coluna. A grade 3-por-3, por exemplo, tem conjunto de arestas 0-1 1-2 3-4 4-5 6-7 7-8 0-3 3-6 1-4 4-7 2-5 5-8. Escreva uma função UGRAPHrandGrid() que construa uma grade não-dirigida m-por-n. Use uma permutação aleatória de 0..V-1 para dar nomes aos vértices. (Quantas arestas terá a grade?)
★ Cubo (não-dirigido). O cubo de dimensão n é o grafo não-dirigido com vértices 0 1 2 ... 2ⁿ-1 cujas arestas são definidas assim: dois vértices v e w são adjacentes se e somente se as expansões binárias dos números v e w diferem em exatamente um bit. (Veja a página http://en.wikipedia.org/wiki/Cube_graph.) Escreva uma função UGRAPHbuildCube() que construa o cubo de dimensão n.

Tipo-de-dados abstrato

Mostramos acima duas maneiras de representar um grafo. O modo como fizemos isso aponta para a possibilidade de tratar grafos como tipo-de-dados abstrato (= ADT = abstract data type). Um tipo-de-dados abstrato permitiria isolar os programas que usam grafos dos detalhes da implementação do conceito: um usuário poderia escrever sua aplicação sem saber como o grafo é implementado.

Entretanto, as implementações descritas neste capítulo não chegam a definir um tipo-de-dados abstrato pois o usuário não pode ignorar completamente os detalhes da representação utilizada. Assim, a ideia de tratar grafos como um tipo-de-dados abstrato não será levada a sério neste sítio.

Exercícios 5: bibliotecas

★ Prepare uma biblioteca de funções GRAPHmatrix para trabalhar com grafos representados por matriz de adjacências. Comece por colocar em um módulo GRAPHmatrix.c as funções discutidas no texto e nos exercícios deste capítulo. Depois, digite a interface GRAPHmatrix.h da biblioteca, contendo as estruturas de dados, etc. Prepare um programa cliente para testar a biblioteca. Atualize e aumente a biblioteca e o programa de testes à medida que for estudando os demais capítulos deste sítio.
★ Prepare uma biblioteca de funções GRAPHlists para trabalhar com grafos representados por listas de adjacência. Adapte as instruções do exercício anterior. [Solução parcial]

Subgrafos

Suponha, por exemplo, que G é um grafo com vértices 0 1 2 ... 99. Se dissermos que H é um subgrafo de G e tem 5 vértices, ficará subentendido que a representação de H está embutida na representação de G e que os vértices de H não são necessariamente 0 1 2 3 4, podendo ser 11 22 33 55 88, por exemplo.

Entrada de dados

Um arquivo de arcos é um arquivo de texto que tem o seguinte formato: A primeira linha do arquivo contém um inteiro estritamente positivo V, a segunda linha contém um inteiro positivo A, e cada uma das A linhas seguintes contém dois inteiros pertencentes ao intervalo 0..V-1. Eis um exemplo:

(O último caractere do arquivo é um \n.) Se interpretarmos cada linha do arquivo como um arco, podemos dizer que o arquivo descreve um grafo com vértices 0..V-1.

Um arquivo de adjacências é um arquivo de texto que tem o seguinte formato: A primeira linha do arquivo contém um inteiro estritamente positivo V e cada uma das V linhas subsequentes contém um inteiro positivo seguido de zero ou mais outros inteiros, todos entre 0 e V-1. Eis um exemplo:

(O último caractere do arquivo é um \n.) Um arquivo de adjacências descreve um grafo com vértices 0..V-1. As últimas V linhas do arquivo definem os arcos do grafo: a linha que começa com v contém a lista de todos os vizinhos de v.

Exercícios 7: entrada de dados

Escreva uma função GRAPHinputArcs() que receba um arquivo de arcos e construa uma representação do grafo. Use as funções GRAPHinit() e GRAPHinsertArc().
Escreva uma função GRAPHinputAdjLists() que receba um arquivo de adjacências construa a representação do correspondente grafo. Use as funções GRAPHinit() e GRAPHinsertArc().
Torneio. Digite um arquivo de adjacências que contenha a descrição de um torneio com 6 vértices.
3-Cubo. Digite um arquivo de adjacências que contenha a descrição de um cubo de dimensão 3.
Atualize suas bibliotecas. Acrescente as funções sugeridas nesta página à biblioteca GRAPHmatrix. Também acrescente as versões apropriadas à biblioteca GRAPHlists. Atualize os correspondentes arquivos-interface.

Perguntas e respostas

Pergunta: Por que não usar uma representação de grafos que consiste simplesmente em um vetor de arcos (em ordem arbitrária)?
Resposta: É um bom exercício preencher os detalhes dessa representação. Ela ocupa menos espaço que uma matriz de adjacências e um vetor de listas de adjacência. Entretanto, essa representação não se presta a implementações eficientes de algoritmos que manipulam grafos.
Pergunta: Por que não usar typedef (em lugar de #define) para definir o tipo-de-dados vertex?
Resposta: Se fizesse isso, eu me sentiria na obrigação de tratar vertex como um tipo-de-dados sério e portanto teria que distinguir as constantes do tipo vertex das correspondentes constantes do tipo int (por exemplo, a constante 0 do tipo vertex da constante 0 do tipo int). Isso tornaria tudo muito pesado.
Pergunta: Posso escrever for (v = 0; v < G->V; ++v){ ? Posso escrever for (v=0;v<G->V;++v) { ?
Resposta: Não. Por acaso você escreve queromeespecializaremcomputaçãográfica, tudo junto?
Pergunta: Posso escrever for(v = 0; v < G->V; ++v) { ?
Resposta: Não. Não há razão para grudar for com ( pois for é um operador e não uma função.
Pergunta: Qual a diferença entre for (i = 0; i < n; ++i) e for (i = 0; i < n; i++) ?
Resposta: Nenhuma. Eu gosto mais da primeira forma, mas a segunda tem o mesmo efeito.
Pergunta: Como o compilador interpreta a expressão G->adj[v] ?
Resposta: A única interpretação razoável é (G->adj)[v] . A alternativa G->(adj[v]) nem faz sentido.
Pergunta: Quando escrevemos algo como o vetor g[] bla bla no meio de um texto em português, não deveríamos eliminar o par de colchetes depois do nome do vetor? Afinal, o nome do vetor é g e não g[].
Resposta: Concordo. Entretanto, sou forçado a reconhecer que o par de colchetes é útil para deixar claro que g é um vetor e não uma variável escalar.
Pergunta: Por que escrever GRAPHshow( Graph G) com espaço depois do parêntese esquerdo? Não deveria ser GRAPHshow(Graph G), ou talvez GRAPHshow (Graph G)? A mesma pergunta se aplica a todas as chamadas de funções, como MATRIXint( r, c, 0) por exemplo.
Resposta: Eu prefiro não escrever GRAPHshow( Graph G) porque em matemática não se deixa espaço entre o nome de uma função e os seus argumentos. Também prefiro não escrever GRAPHshow(Graph G) para não grudar o nome da função com o primeiro argumento, coisa que dificultaria a leitura. (Mas é preciso lembrar que o compilador C ignora espaços e portanto aceita qualquer das formas.)
Pergunta: O que significa o prefixo UGRAPH dos nomes de algumas funções?
Resposta: As funções que manipulam grafos têm prefixo GRAPH. As que são restritas a grafos não-dirigidos (undirected) têm prefixo UGRAPH.

Estruturas de dados para grafos