Algoritmos para Grafos | Índice
O conceito de componente aresta-biconexa
de um grafo não-dirigido generaliza o conceito de
componente conexa.
Uma componente aresta-biconexa
de um grafo não-dirigido
é uma parte do grafo que tem forte coesão interna
mas fraca ligação
com o resto do grafo.
As componentes aresta-biconexas de um grafo não-dirigido poderiam ser definidas como classes de equivalência da seguinte relação de ligação dupla entre vértices: dois vértices s e t estão duplamente ligados se existem dois caminhos de s a t sem arestas em comum. Essa definição é natural e intuitiva mas é difícil de manejar. Por isso, adotaremos abaixo uma definição equivalente que é mais cômoda.
Este capítulo trata do problema de encontrar as componentes aresta-biconexas de um grafo não-dirigido. Em especial, discute um algoritmo eficiente para o problema.
Sumário:
Uma componente aresta-biconexa (= edge-biconnected component = 2-edge-connected component) de um grafo não-dirigido G é um subgrafo aresta-biconexo maximal de G. Um subgrafo aresta-biconexo H de G é maximal se não existe grafo aresta-biconexo H' tal que H ⊂ H' ⊆ G, ou seja, não existe subgrafo aresta-biconexo H' de G que contenha H e seja maior que H.
As seguinte propriedades das componentes aresta-biconexas de grafos não-dirigidos seguem imediatamente da definição:
Portanto, as componentes aresta-biconexas determinam uma partição do conjunto de vértices do grafo e cada componente aresta-biconexa é induzida por um dos blocos da partição.
Componentes versus pontes. É claro que toda aresta de uma componente aresta-biconexa pertence a um circuito. Reciprocamente, toda aresta do grafo que pertence a um circuito também pertence a alguma componente aresta-biconexa. Em outras palavras, uma aresta de um grafo é uma ponte se e somente se suas pontas estão em duas componentes aresta-biconexas distintas. (Convém lembrar que uma ponte é, por definição, qualquer aresta que não pertence a um circuito.)
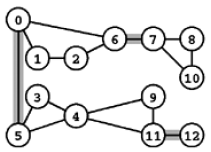
Exemplo A. O grafo da figura tem 4 componentes aresta-biconexas. Os conjuntos de vértices dessas componentes são 0 1 2 6, 3 4 5 9 11, 7 8 10 e 12. As arestas 0-5, 6-7 e 11-12 são pontes. As pontes ligam componentes aresta-biconexas distintas.
O grafo das componentes aresta-biconexas de G é o grafo não-dirigido B(G) definido assim: os vértices de B(G) são as componentes aresta-biconexas de G e há uma aresta I–J em B(G) se e somente se I é diferente de J e alguma aresta de G tem uma ponta em I e outra em J. É claro que as arestas de B(G) correspondem às pontes de G.
É fácil verificar que o grafo B(G) não tem circuitos, ou seja, que é uma floresta. Por isso, B(G) é às vezes chamado floresta das componentes aresta-biconexas de G. Qualquer grafo não-dirigido pode ser visto como uma floresta em que cada vértice foi substituído por um grafo aresta-biconexo.
Exemplo B. Seja G o grafo não-dirigido representado na figura. Os quatro vértices do grafo B(G) correspondem aos conjuntos de vértices
0 2 3 8 1 4 7 10 5 6 9
de G. Escreva a lista de arcos do grafo B(G). Verifique que B(G) é uma floresta.
Em muitas aplicações de grafos não-dirigidos, é vantajoso processar cada componente aresta-biconexa em separado. Por isso, a habilidade de encontrar todas as componentes aresta-biconexas é muito útil.
Problema das componentes aresta-biconexas: Encontrar todas as componentes aresta-biconexas de um grafo não-dirigido.
A relação entre componentes aresta-biconexas e pontes mostra o seguinte: Se P é o conjunto de todas as pontes de um grafo G então cada componente conexa de G−P é uma componente aresta-biconexa de G e vice-versa. Essa observação pode ser usada para resolver o problema. Mas se as pontes forem calculadas de maneira ingênua, o algoritmo resultante será muito lento.
Para obter um algoritmo mais rápido, é preciso recorrer a um algoritmo rápido de cálculo de pontes. (Veja o capítulo Grafos aresta-biconexos e o exercício Lista de pontes.) Faremos isso nas próximas seções.
Robert Tarjan mostrou (1974) como uma busca DFS pode ser usada para encontrar eficientemente as componentes aresta-biconexas de um grafo. O algoritmo de Tarjan é uma extensão do algoritmo que decide se um grafo é aresta-biconexo (veja o capítulo Grafos aresta-biconexos).
Antes de examinar o algoritmo,
é necessário entender a relação entre florestas DFS e componentes aresta-biconexas.
Suponha que um grafo é submetido a uma busca DFS.
A cabeça de uma componente aresta-biconexa
é o primeiro vértice da componente a ser descoberto pela busca.
Em outras palavras,
a cabeça é o vértice da componente que tem o menor número de pré-ordem.
Podemos dizer que a cabeça é a porta de entrada
da componente.
A cabeça de uma componente aresta-biconexa é (1) uma raiz da floresta DFS ou (2) a ponta final de um arco da floresta DFS cuja ponta inicial está em outra componente. No caso (2), o arco da floresta que entra na componente faz parte de uma ponte do grafo.
Segue da definição da busca DFS que todos os vértices de uma componente aresta-biconexa descendem, na floresta DFS, da cabeça da componente. Além disso, se c é a cabeça de uma componente aresta-biconexa K então, para qualquer vértice x de K, todos os vértices do caminho que vai de c a x na floresta DFS pertencem a K. Essas duas propriedades podem ser resumidas assim:
Propriedade DFS das componentes aresta-biconexas: Para qualquer floresta DFS de um grafo não-dirigido, a subfloresta induzida pelo conjunto de vértices de qualquer componente aresta-biconexa do grafo é uma árvore radicada.
Se removermos os arcos da floresta DFS que entram nas cabeças de componentes aresta-biconexas, teremos uma coleção de árvores radicadas. De acordo com a propriedade acima, cada uma dessas árvores corresponde, exatamente, a uma componente aresta-biconexa do grafo.
Exemplo C. Considere o grafo não-dirigido definido pelas listas de adjacência abaixo. Veja ao lado uma floresta DFS do grafo (você deve imaginar que todos os arcos da figura estão dirigidos de cima para baixo).
0
/ \
1 6
/ \ \
2 4 7
/ \
3 5
0: 1 6 7 1: 0 2 4 5 2: 1 3 3: 2 4: 1 5 5: 1 4 6: 0 7 7: 0 6
As únicas arestas do grafo que não constam da figura são 0-7 e 1-5. Acrescente essas arestas à figura e constate que o grafo tem quatro componentes aresta-biconexas. Essas componentes são induzidas pelos conjuntos de vértices
0 6 7 1 4 5 2 3
Observe que os vértices de cada um desses conjuntos não estão espalhados pela floresta, uns longe dos outros. Mais precisamente, a subfloresta induzida por cada um desses conjuntos de vértices é uma árvore radicada.
As cabeças das componentes aresta-biconexas são 0, 1, 2 e 3 respectivamente. Note a ordem em que a busca DFS percorre as várias componentes: primeiro visita um vértice da componente 0 6 7, depois um vértice da componente 1 4 5, depois a componente 2, depois a componente 3, depois os vértices restantes da componente 1 4 5, e finalmente os vértices restantes da componente 0 6 7.
Considere a floresta DFS produzida por uma busca DFS num grafo não-dirigido. Digamos que c0, c1, … , cn−1 são as cabeças das componentes aresta-biconexas do grafo. Suponha que essa lista de cabeças está em pós-ordem. Assim, c0 é a primeira cabeça a morrer — ou seja, a primeira a terminar de ser processada pela função dfsR() — e cn−1 é a última. Para cada i, seja Ki a componente aresta-biconexa cuja cabeça é ci. Não é difícil deduzir da propriedade DFS das componentes aresta-biconexas que K0 é induzida pelo conjunto de todos os descendentes de c0. Já K1 é induzida pelo conjunto de descendentes de c1 que não estão em K0. Da mesma forma, K2 é induzida pelo conjunto de descendentes de c2 que não estão em K0 ∪ K1. Finalmente, Kn−1 é induzida pelo conjunto de descendentes de cn−1 que não estão em K0 ∪ … ∪ Kn−2.
Essas observações são a base do algoritmo de Tarjan. Para implementar o algoritmo, basta saber distinguir uma cabeça de um outro vértice qualquer. Como já observamos acima, toda cabeça é a ponta final de um arco de floresta que faz parte de uma ponte (exceto se a cabeça é uma raiz da floresta). Portanto, um vértice v é uma cabeça se e somente se
lo[v] ≡ pre[v],
sendo lo[] a numeração lowest preorder number discutida na seção Número de pré-ordem mínimo do capítulo Grafos aresta-biconexos. Aquela seção também mostrou uma função UGRAPHlo() que calcula a numeração lo[].
Feitas essas observações, podemos escrever o código da função UGRAPHebiconComps3() que implementa o algoritmo de Tarjan. Para marcar as componentes aresta-biconexas, vamos atribuir um número a cada componente e rotular cada vértice com o número da componente a que ele pertence. (Diremos que qualquer numeração desse tipo identifica as componentes aresta-biconexas do grafo.)
static int pre[1000], post[1000]; static int cnt, cntt; static vertex pa[1000]; static int lo[1000]; int ebc[1000];
/* A função UGRAPHebiconComps3() devolve o número (quantidade) de componentes aresta-biconexas do grafo não-dirigido G e armazena no vetor ebc[] uma numeração dos vértices dotada da seguinte propriedade: ebc[v] == ebc[w] se e somente se v e w estão na mesma componente. */
int UGRAPHebiconComps3( UGraph G) { UGRAPHlo( G); // calcula lo[] // também calcula pre[], post[] e pa[] for (vertex v = 0; v < G->V; ++v) ebc[v] = -1; vertex vv[1000]; for (vertex v = 0; v < G->V; ++v) vv[post[v]] = v; // vv[0..V-1] é permutação em pós-ordem int id = 0; for (int j = 0; j < G->V; ++j) { vertex v = vv[j]; if (lo[v] == pre[v]) // ebc[v] == -1 // v é cabeça de componente ebiconCompR( G, v, id++); } return id; }
/* Esta função faz ebc[x] = id para todo vértice x que seja descendente de v na floresta radicada representada por pa[] e tenha ebc[x] == -1. */
static void ebiconCompR( UGraph G, vertex v, int id) { ebc[v] = id; for (link a = G->adj[v]; a != NULL; a = a->next) { vertex w = a->w; if (pa[w] == v && ebc[w] == -1) ebiconCompR( G, w, id); } }
Exemplo D. Considere o grafo não-dirigido com vértices a b c d e f g h i j e as seguintes listas de adjacência:
a: b h b: c d a c: d h i b d: e b c e: f g d f: g e g: e f h: i a c i: j c h j: i
Veja a seguir a floresta DFS e os vetores pre[], post[] e lo[] produzidos pela função UGRAPHlo(). (Os vértices estão em pós-ordem na primeira linha da tabela.)
v g f e d h i j c b a
pre[v] 6 5 4 3 7 8 9 2 1 0
post[v] 0 1 2 3 4 5 6 7 8 9
lo[v] 4 4 4 1 0 2 9 0 0 0
0a0
|
1b0
|
2c0
/ \
3d1 7h0
/ \
4e4 8i2
/ \
5f4 9j9
/
6g4
Na figura da floresta, cada vértice v tem à sua esquerda o número pre[v] e à sua direita o número lo[v]. Confira os números depois de acrescentar à figura as demais arestas do grafo: a-h b-d c-i e-g. Como o grafo é não-dirigido, todas as arestas que não pertencem à floresta DFS ligam um ancestral a um descendente.
Os vértices e j a são as cabeças das três componentes aresta-biconexas. As arestas i-j e d-e são as únicas pontes do grafo. A função UGRAPHebiconComps3() examina os vértices na ordem g f e d h i j c b a e portanto encontra primeiro a cabeça e, depois a cabeça j e finalmente a cabeça a. Portanto, atribui o número 0 aos vértices da componente aresta-biconexa e f g, depois atribui o número 1 ao único vértice da componente j, e finalmente atribui o número 2 aos vértices da componente a b c d h i. Com isso, o vetor ebc[] ficará no seguinte estado:
v g f e d h i j c b a
ebc[v] 0 0 0 2 2 2 1 2 2 2
0
|
1
|
2
/ \
3 6
/
4
/
5
Exemplo E. Considere o grafo não-dirigido definido pelas listas de adjacência abaixo. Veja ao lado a figura de uma floresta DFS do grafo.
0: 1 1: 0 2 6 2: 1 3 6 3: 2 4 5 4: 3 5 5: 3 4 6: 1 2
Como o grafo é não-dirigido, todas as arestas que não pertencem à floresta DFS ligam um ancestral a um descendente. Basta acrescentar essas arestas à figura da floresta para perceber que as componentes aresta-biconexas são induzidas pelos conjuntos de vértices
3 4 5 1 2 6 0
Veja o resultado da função UGRAPHlo() e o estado final do vetor ebcc[]:
v 0 1 2 3 4 5 6
pre[v] 0 1 2 3 4 5 6
post[v] 6 5 4 2 1 0 3
lo[v] 0 1 1 2 3 3 1
ebc[v] 2 1 1 0 0 0 1
Ao invocar UGRAPHlo(), a função UGRAPHebiconComps3() examina o grafo todo duas vezes. Embora isso resulte em um algoritmo linear, é preferível obter o mesmo efeito examinando o grafo apenas uma só vez. Para fazer isso, é preciso que as componentes aresta-biconexas sejam rotulados durante a busca DFS que calcula lo[] e não depois dela. Não é óbvio como fazer isso, uma vez que a busca DFS não descobre uma componente aresta-biconexa completa de uma só vez: ela descobre alguns vértices de uma componente, depois alguns vértices de outra, depois alguns vértices de mais outra, até que finalmente volta a descobrir os vértices restantes da primeira componente.
Para lidar com essa dificuldade, será necessário armazenar temporariamente, em uma pilha, todos os vértices descobertos durante o intervalo de vida da cabeça da componente. Quando a cabeça morrer, os vértices da correspondente componente estarão todos na pilha. A pilha pode ser compartilhada por várias componentes diferentes. Quando alguma cabeça v morrer, todos os vértices da componente de v estarão armazenados acima de v na pilha, podendo então ser rotulados e removidos da pilha. A função a seguir usa um vetor stack[0..t-1] para implementar a pilha de vértices.
static int pre[1000], lo[1000]; static vertex pa[1000], stack[1000]; static int t, cnt, id; int ebc[1000]; #define min( A, B) (A) < (B) ? (A) : (B);
/* A função UGRAPHebiconComps() devolve o número de componentes aresta-biconexas do grafo não-dirigido G e armazena no vetor ebc[] uma numeração dos vértices tal que ebc[v] == ebc[w] se e somente se v e w estão na mesma componente. (A função implementa o algoritmo de Tarjan.) */
int UGRAPHebiconComps( UGraph G) { for (vertex v = 0; v < G->V; ++v) pre[v] = -1; t = cnt = id = 0; for (vertex v = 0; v < G->V; ++v) if (pre[v] == -1) { // nova etapa pa[v] = v; dfsRebiconComps( G, v); } return id; }
/* Para todo vértice u na pilha de vértices stack[0..t-1] tem-se pre[u] != -1 e ebc[u] == -1. (O código de dfsRebiconComps() foi adaptado da figura 5.15 do livro de Aho, Hopcroft e Ullman.) */
static void dfsRebiconComps( UGraph G, vertex v) { pre[v] = cnt++; stack[t++] = v; lo[v] = pre[v]; for (link a = G->adj[v]; a != NULL; a = a->next) { vertex w = a->w; if (pre[w] == -1) { // 1 pa[w] = v; // 2 dfsRebiconComps( G, w); // 3 (calcula lo[w]) lo[v] = min( lo[v], lo[w]); // 4 } else { // 6 if (w != pa[v]) // 7 lo[v] = min( lo[v], pre[w]); // 8 } // 9 } // 10 if (lo[v] == pre[v]) { // v é uma cabeça vertex u; do { u = stack[--t]; ebc[u] = id; } while (u != v); id++; } // 18 }
As linhas 1 a 9 do código aplicam a fórmula recursiva para lo[] discutida no capítulo Grafos aresta-biconexos. A linha 4 aplica o primeiro item da fórmula recursiva usando o valor de lo[w] que acabou de ser calculado na linha 3. Na linha 7, o arco v-w abraça v. Portanto, a linha 8 aplica o segundo item da fórmula recursiva.
No início de cada invocação de dfsRebiconComps(), a pilha stack[0..t-1] tem a seguinte propriedade: para quaisquer dois índices j e k tais que 0 ≤ j < k ≤ t, se stack[j] é a única cabeça de componente em stack[j..k-1] então todos os vértices em stack[j..k-1] pertencem à mesma componente. (Mas stack[j..k-1] pode não conter todos os vértices da componente.)
a
|
b
|
c
/ \
d g
/
e
/
f
Exemplo F. Considere novamente o exemplo E. Para que o exemplo fique mais legível, adote nomes alfabéticos para os vértices. Veja as listas de adjacência e uma floresta DFS do grafo:
a: b b: a c g c: b d g d: c e f e: d f f: d e g: b c
Veja o rastreamento da execução da versão on-the-fly da função UGRAPHebiconComps():
stack componente
a dfsRebiconComps(a) a
a-b dfsRebiconComps(b) ab
b-a
b-c dfsRebiconComps(c) abc
c-b
c-d dfsRebiconComps(d) abcd
d-c
d-e dfsRebiconComps(e) abcde
e-d
e-f dfsRebiconComps(f) abcdef
f-d
f-e
f (lo=3) abcdef
e (lo=3) abcdef
d-f
d (lo=3) abc fed
c-g dfsRebiconComps(g) abcg
g-b
g-c
g (lo=1) abcg
c (lo=1) abcg
b-g
b (lo=1) a gcb
a (lo=0) a
Nas linhas do rastreamento que começam com um
v dfsRebiconComps(v)
ou um u-v dfsRebiconComps(v),
a coluna stack dá o estado da pilha
stack[0..t-1] no fim da
linha stack[t++] = v
do código.
Cada linha do rastreamento que tem apenas um v-w na primeira coluna representa o processamento do arco v-w pelo bloco de linhas 7-8 do código.
Cada linha do rastreamento que tem apenas um v (lo=i) na primeira coluna marca o fim do processamento do vértice v (fim da linha 10 do código). Nessa ocasião, i é o valor de lo[v]. A coluna stack dá o estado da pilha stack[0..t-1] na linha 18 e a coluna componente dá os vértices da nova componente descoberta se lo[v] ≡ pre[v].
No fim da execução da função, os vetores pre[], lo[] e ebc[] estarão no seguinte estado:
v a b c d e f g
pre[v] 0 1 2 3 4 5 6
lo[v] 0 1 1 3 3 3 1
ebc[v] 2 1 1 0 0 0 1
a
/
b
/
c
/
d
Exemplo G. Considere o grafo não-dirigido definido pelas listas de adjacência abaixo. Veja ao lado uma floresta DFS do grafo.
a: b c b: a c d c: a b d d: b c
Veja o rastreamento da execução da função UGRAPHebiconComps():
stack componente
a dfsRebiconComps(a) a
a-b dfsRebiconComps(b) ab
b-a
b-c dfsRebiconComps(c) abc
c-a
c-b
c-d dfsRebiconComps(d) abcd
d-b
d-c
d (lo=1)
c (lo=0)
b (lo=0)
a (lo=0) dcba
0a0
/
1b0
/
2c0
/
3d1
O rastreamento mostra que a é a cabeça da única componente aresta-biconexa. A figura à direita mostra a floresta DFS com os valores de pre[] e lo[]: cada vértice v é precedido pelo valor de pre[v] e seguido pelo valor de lo[v].
grafo-caminho0-1-2-3-4-5-6-7-8-9. Aplique a função UGRAPHebiconComps() ao
grafo-circuito0-1-2-3-4-5-6-7-8-9-0. Explique o que acontece em cada linha do código da função.
trevo de 3 folhasdefinido pelas arestas 0-1 1-0 1-2 2-1 1-3 3-2. Faça o rastreamento da execução da função.
b: a a: b c c: a d d: c
a: b b: e c a c: j e d b d: e c e: h g f d c b f: e g g: f e h: j i e i: h j: c h
0: 6 5 1 1: 2 0 2: 6 1 3: 4 5 4: 5 11 3 9 5: 0 4 3 6: 7 2 0 7: 10 8 6 8: 10 7 9: 11 4 10: 8 7 11: 4 12 9 12: 11
0: 2 3 1: 8 2: 8 3 0 3: 8 0 2 4: 9 7 10 5: 6 9 6: 5 9 7: 4 10 8: 1 10 2 3 9: 5 6 4 10: 4 7 8
do ... while (u != v)em dfsRebiconComps() não corre o risco de ultrapassar o fundo da pilha stack[0..t-1]. Em outras palavras, mostre que v está na pilha quando o processo iterativo começa.
A função UGRAPHebiconComps() consiste essencialmente em uma busca em profundidade. Assim, o consumo de tempo é proporcional a
V + E
no pior caso, sendo V o número de vértices e E o número de arestas do grafo. (Se o grafo é conexo, podemos dizer que o consumo de tempo é proporcional a E.) O algoritmo é, portanto, linear no tamanho do grafo.