Algoritmo de Tarjan para componentes fortes de grafos

Este capítulo discute um algoritmo para do problema das componentes fortes (= strong components), que já foi apresentado no capítulo Componentes fortes.

Cabeças de componentes fortes

Durante uma busca DFS, a cabeça de uma componente forte é o vértice da componente que tem o menor número de pré-ordem, ou seja, a cabeça é o primeiro vértice da componente a ser descoberto pela busca. Podemos dizer que a cabeça é a porta de entrada da componente. (Mas a cabeça não é uma propriedade intrínseca da componente, já que diferentes buscas DFS podem escolher diferentes cabeças.)

Segue da definição da busca DFS (veja a documentação da função dfsR()) que todos os vértices de uma componente forte são descendentes da cabeça da componente na floresta DFS. Além disso, se r é a cabeça de uma componente forte K então, para qualquer vértice x de K, todos os vértices do caminho que vai de r a x na floresta DFS pertencem a K. Essas duas propriedades podem ser resumidas assim:

Se removermos da floresta DFS os arcos que entram nas cabeças de componentes fortes (há no máximo um arco desse tipo para cada cabeça), teremos uma coleção de árvores radicadas. De acordo com a propriedade acima, cada uma dessas árvores corresponde, exatamente, a uma componente forte do grafo.

Exemplo A. Considere o grafo definido pelas listas de adjacência abaixo. Veja ao lado uma floresta DFS do grafo (você deve imaginar que todos os arcos da floresta estão dirigidos de cima para baixo na figura).

Os únicos arcos do grafo que não estão na figura são 2-1, 5-2, 4-3, 7-3, 7-6 e 8-7. Acrescente esses arcos à figura para constatar que o grafo tem cinco componentes fortes e que essas componentes são induzidas pelos seguintes conjuntos de vértices:

Observe que os vértices de cada um desses conjuntos não estão espalhados pela floresta, uns longe dos outros. Mais precisamente, a subfloresta induzida por cada um desses conjuntos de vértices é uma árvore radicada.

As cabeças das componentes são 3, 1, 9, 6 e 0 respectivamente. Note a maneira como a busca DFS percorre as cinco componentes: primeiro visita o único vértice da componente 0, depois visita alguns vértices da componente 1 2 5, depois os vértices da componente 3 4, depois outro vértice da componente 1 2 5, depois alguns vértices da componente 6 7 8, depois o vértice da componente 9, e finalmente o vértice restante da componente 6 7 8.

Exercícios 1

Faça uma busca DFS num grafo. Seja r a cabeça de alguma componente forte K. É verdade que todos os descendentes de r na floresta DFS pertencem a K? É verdade algum dos caminhos na floresta DFS que começam em r contém todos os vértices de K?
É verdade que uma busca DFS descobre todos os vértices de uma componente forte, depois todos os vértices de outra componente forte, e assim por diante?
Dags. Mostre que num dag cada vértice é cabeça de uma componente forte (qualquer que seja a floresta DFS escolhida).
★ Seja u-v um arco da floresta DFS de um grafo. Suponha que um ciclo passa por u-v. Mostre que v não é cabeça de uma componente forte.
Cada linha da tabela abaixo dá a lista de arcos de um grafo. Faça uma busca DFS em cada um dos grafos. Em cada caso, mostre a floresta DFS, as componentes fortes, e suas cabeças.
```
0-1 1-2 2-0 3-4 4-5 5-3 3-2
0-1 1-5 5-0 2-3 3-4 4-2 1-2
0-1 1-2 2-0 3-4 4-5 5-3 6-7 7-8 8-6 3-1 6-0 7-5
0-1 1-2 2-0 3-7 7-8 8-3 7-4 4-5 5-6 6-4 4-2
```
Prova da propriedade DFS. Prove a propriedade DFS das componentes fortes. [Solução]

Preliminares

Considere a floresta DFS produzida por uma busca DFS num grafo. Sejam r₀, r₁, … , r_n−1 as cabeças das componentes fortes do grafo. Suponha que essa lista de cabeças está em pós-ordem inversa. Assim, r_n−1 é a primeira cabeça a morrer — ou seja, a primeira a terminar de ser processada pela função dfsR() — e r₀ é a última.

Para cada i, seja K_i a componente forte cuja cabeça é r_i. Não é difícil deduzir da propriedade DFS das componentes fortes que K_n−1 é induzida pelo conjunto de todos os descendentes de r_n−1 na floresta DFS. Já K_n−2 é induzida pelo conjunto de descendentes de r_n−2 que não estão em K_n−1. Da mesma forma, K_n−3 é induzida pelo conjunto de descendentes de r_n−3 que não estão em K_n−1 ∪ K_n−2. Finalmente, K₀ é induzida pelo conjunto de descendentes de r₀ que não estão em K_n−1 ∪ … ∪ K₁.

Essas observações são a base do algoritmo de Tarjan. A principal dificuldade do algoritmo é reconhecer as cabeças das componentes fortes, ou seja, distinguir uma cabeça de um vértice comum.

Não há como reconhecer uma cabeça no momento em que ela é descoberta pela busca DFS; é preciso esperar pelo momento em que a cabeça morre. Por isso será necessário armazenar, em algum vetor, todos os vértices descobertos durante o intervalo de vida da cabeça. Quando a cabeça for reconhecida como tal, os vértices da correspondente componente estarão todos no vetor. Se o vetor for administrado como uma pilha, poderá ser naturalmente compartilhado por todas as componentes. Quando um determinado vértice v da pilha for reconhecido como cabeça, todos os vértices da componente de v estarão armazenados acima de v na pilha, podendo então ser removidos da pilha e impressos. (Essa pilha é análoga à usada pelo algoritmo de Tarjan para componentes aresta-biconexas.)

Exercícios 2

Dada uma floresta DFS F de um grafo G, suponha que o gênio da lâmpada maravilhosa de Aladim nos fornece a lista r[0], r[1], … , r[n-1] das cabeças (em relação a F) das componentes fortes de G. Suponha ainda que o gênio fornece essa lista em pós-ordem. Escreva uma função que receba G e r[0..n-1] e imprima o conjunto de vértices de cada componente forte de G.

Caracterização das cabeças

Para reconhecer uma cabeça de componente forte, o algoritmo de Tarjan usa o conceito de abraço. Dada uma floresta DFS de um grafo, diremos que um arco x-y do grafo abraça um vértice v da floresta se

(Em virtude da condição 3 da definição, esse conceito de abraço é bem mais restritivo que aquele usado pelo algoritmo que decide conexão forte no capítulo Grafos fortemente conexos.) A inexistência de abraços caracteriza as cabeças de componentes fortes, ou seja, fornece um critério para decidir se um dado vértice é uma cabeça.

Eis um esboço da prova do lema: Se um arco x-y abraça v, existe um passeio de v até algum ancestral próprio r de v. Como existe um caminho de r a v, os vértices r e v pertencem à mesma componente forte. Como r é diferente de v, esse último não é cabeça da componente.

À primeira vista, o critério fornecido pelo lema parece computacionalmente pesado: para cada vértice v, todos os arcos do grafo deveriam ser testados. Mas é possível organizar os cálculos de modo a testar cada arco uma única vez (no decurso de uma busca em profundidade). Para fazer isso, a próxima seção introduz o conceito de número de pré-ordem mínimo.

Exemplo B. Seja G o grafo com vértices a..h definido pelas listas de adjacência abaixo. Veja ao lado uma floresta DFS do grafo.

Os únicos arcos do grafo que não estão na floresta são e-b, f-d, h-f. O arco e-b abraça os vértices e, d, c. O arco f-d abraça f bem como e. O arco h-f abraça g (veja o caminho f-d-e-b). O arco h-f também abraça h. Portanto, os vértices a e b são as únicas cabeças.

Exercícios 3

★ Suponha que um arco x-y do grafo abraça um vértice v. Mostre que pre[y] < pre[v]. Mostre também que pre[y] < pre[x] e portanto x-y é cruzado ou de retorno. Mostre ainda que a cabeça da componente forte de y é ancestral próprio de v.
Mostre que a condição 2 na definição de abraço pode ser trocada pela seguinte: y é primo esquerdo ou ancestral próprio de v. Mostre que a condição 3 na definição de abraço pode ser trocada pela seguinte: a cabeça da componente forte de y é ancestral de v.
Prova do lema. Prove o lema do abraço. (A prova usa a propriedade DFS das componentes fortes). [Solução]

Números de pré-ordem mínimos

O lema do abraço oferece um critério para reconhecer cabeças de componentes fortes. Para que esse critério possa ser aplicado eficientemente, é preciso introduzir o seguinte conceito auxiliar. O número de pré-ordem mínimo (= lowest preorder number) de um vértice v é o número lo[v] assim definido:

sendo o mínimo tomado sobre todos os arcos x-y que abraçam v. (Muitos livros escrevem low no lugar do meu lo.) Note que lo[v] < pre[v] sempre que algum arco abraça v (veja exercício acima). Se nenhum arco abraça v então, de acordo com a definição, lo[v] é infinito; mas é mais conveniente adotar a definição especial lo[v] = pre[v] nesse caso. Desse modo, teremos lo[v] ≤ pre[v] para todo vértice v sem exceção.

O lema do abraço pode agora ser reformulado em termos da numeração lo[]: Um vértice v é cabeça de uma componente forte se e somente se

Essa reformulação haverá de permitir o reconhecimento eficiente de cabeças de componentes fortes.

Exemplo C. Considere novamente o grafo do exemplo B, definido pelas seguintes listas de adjacência:

A figura à direita mostra uma floresta DFS do grafo em que cada vértice v é precedido pelo número pre[v] e seguido do número lo[v]. Lembre-se de que os únicos arcos do grafo que não estão na floresta são e-b, f-d e h-f. Confira os valores de lo[]!

Cálculo eficiente de lo[ ]. Para calcular lo[] eficientemente durante a busca DFS, usaremos a seguinte fórmula recursiva, que exprime o valor de lo[] em v em função dos valores que lo[] nos filhos de v. Para cada vértice v, lo[v] é o menor dentre os números dos seguintes tipos:

O primeiro e o segundo itens da fórmula podem ser vazios. Se ambos forem vazios então lo[v] = pre[v]. O segundo e o terceiro itens da fórmula constituem a base da recursão. A prova cuidadosa da fórmula é um bom exercício.

A fórmula recursiva calcula lo[] em pós-ordem: se a permutação dos vértices em pós-ordem é i, j, k, … então a fórmula calcula lo[i], depois lo[j], depois lo[k], e assim por diante. Podemos também usar o inverso da permutação em pré-ordem, uma vez que a fórmula só depende da relação entre pais e filhos na floresta DFS.

Infelizmente, a aplicação da fórmula tem uma dificuldade séria: no segundo item da fórmula, não está claro como verificar a condição 3 da definição de abraço, ou seja, como saber se existe um caminho que vai de w até um ancestral próprio de v. Enfrentaremos essa dificuldade na próxima seção.

Exercícios 4

Mostre, diretamente a partir da definição de lo[], que lo[v] ≡ pre[v] se v é uma raiz da floresta DFS.
Considere o grafo-ciclo 0-1-2-3-4-5-6-7-8-9-0. Faça uma busca DFS a partir do vértice 0. Calcule a numeração lo[] diretamente a partir da definição.
Considere o grafo-caminho 0-1-2-3-4-5-6-7-8-9. Faça uma busca DFS a partir do vértice 0. Calcule a numeração lo[] diretamente a partir da definição.
Considere o trevo de 3 folhas definido pelos arcos 0-1 1-0 1-2 2-1 1-3 3-2. Calcule a numeração lo[] diretamente a partir da definição.
Suponha que o grafo em estudo é um dag. Mostre, diretamente a partir da definição de lo[], que lo[v] ≡ pre[v] para cada vértice v.
Faça uma busca DFS a partir do vértice 0 num grafo fortemente conexo. Mostre, diretamente a partir da definição de lo[], que lo[0] ≡ pre[0] e lo[v] < pre[v] para cada vértice v diferente de 0.
★ Seja v um vértice e w um filho de v na floresta DFS do grafo. Prove, diretamente a partir da definição de lo[], que lo[v] ≤ lo[w]. [Solução]
★ Prova da fórmula recursiva. Prove a fórmula recursiva para lo[] dada acima. (Dica: Se w é filho de v então lo[v] ≤ lo[w].)

Implementação do algoritmo

A discussão precedende — cabeças, abraços, numeração lo[] — leva à seguinte função GRAPHstrongCompsT() que implementa o algoritmo de Tarjan. (O sc no nome da função é uma abreviatura de strong component.) A função recebe um grafo G, calcula as componentes fortes do grafo, e armazena num vetor sc[] uma numeração dos vértices que identifica as componentes.

/* A função GRAPHstrongCompsT() devolve o número de componentes fortes 
   do grafo G
   e armazena no vetor sc[],
   indexado pelo vértices de G,
   os rótulos das componentes fortes de G:
   para cada vértice v, sc[v] será o rótulo da 
   componente forte que contém v.
   Os rótulos são 
   0, 1, 2, etc.
   (A função implementa o algoritmo de Tarjan.) */

static int pre[1000], lo[1000];
static vertex stack[1000];
static int t, cnt, k;

int GRAPHstrongCompsT( Graph G, int *sc)
{
   for (vertex v = 0; v < G->V; ++v) 
      pre[v] = sc[v] = -1;
   t = cnt = k = 0;
   for (vertex v = 0; v < G->V; ++v) 
      if (pre[v] == -1)
         dfsRstrongCompsT( G, v, sc);
   return k;
}

A função dfsRstrongCompsT() executa uma busca DFS e administra uma pilha de vértices stack[0..t-1], com topo na posição t-1. Toda vez que descobre um novo vértice v, a função coloca v na pilha e calcula lo[v] usando a fórmula recursiva acima. Quando um vértice v morre (no sentido da busca DFS) a função usa o critério estabelecido acima para decidir se v é a cabeça de uma componente. Em caso afirmativo, todos os vértices da componente estão na pilha entre v e o topo da pilha. Nesse momento, todos esses vértices são removidos da pilha e recebem um mesmo rótulo em sc[].

/* A função dfsRstrongCompsT() visita 
   todos os vértices de G 
   que podem ser alcançados a partir do vértice v
   sem passar por vértices já descobertos.

   A função atribui cnt+k a pre[x]
   se x é o k-ésimo vértice descoberto
   e calcula o valor de lo[x] para cada vértice x
   descoberto.
   (O código foi adaptado 
   da figura 5.15 do livro de Aho, Hopcroft e Ullman.) */

#define min( A, B) (A) < (B) ? (A) : (B)

static void dfsRstrongCompsT( Graph G, vertex v, int *sc)
{
   pre[v] = cnt++;
   stack[t++] = v; // A
   lo[v] = pre[v]; 
   for (link a = G->adj[v]; a != NULL; a = a->next) {
      vertex w = a->w;
      if (pre[w] == -1) { // B
         dfsRstrongCompsT( G, w, sc); // calcula lo[w] // C
         lo[v] = min( lo[v], lo[w]); // D
      }
      else if (pre[w] < pre[v] && sc[w] == -1) { // E
         lo[v] = min( lo[v], pre[w]); // F
      } // G
   } // H
   if (lo[v] == pre[v]) { // v é uma cabeça
      vertex u; // I
      do { // J
         u = stack[--t]; 
         sc[u] = k;
      } while (u != v); // K
      k++;
   }
}

Resta esclarecer, com mais cuidado, como a função usa a fórmula recursiva para calcular o valor de lo[v]. Os primeiro e terceiro itens da fórmula, bem como a parte pre[w] < pre[v] do segundo item, são fáceis de verificar. Mas a condição existe um caminho no grafo que vai de w até um ancestral próprio de v do segundo item é bem mais sutil. Essa condição está satisfeita se w está na pilha, como mostra a propriedade a seguir.

(Eis um esboço da prova da propriedade: Considere o momento em dfsRstrongCompsT(G,v) começa a ser executada. Seja u um vértice da pilha e r a cabeça da componente forte que contém u. A encarnação dfsRstrongCompsT(G,r) certamente já nasceu mas ainda não morreu, pois do contrário r e u já teriam sido removidos da pilha. Logo, o intervalo de vida de dfsRstrongCompsT(G,r) contém o intervalo de vida de dfsRstrongCompsT(G,v), e portanto r é ancestral próprio de v.)

Para saber se w está na pilha, basta verificar se pre[v] já foi definido mas sc[w] ainda não foi definido. Ou seja, basta verificar se pre[w] ≠ -1 mas sc[w] ≡ -1.

Em resumo, o funcionamento de dfsRstrongCompsT() pode ser detalhado como segue. As linhas B a G do código aplicam a fórmula recursiva de lo[]. A linha D aplica o primeiro item da fórmula usando o valor de lo[w] que acabou de ser calculado na linha C. No fim da linha E temos pre[w] ≠ -1 e sc[w] ≡ -1, donde w está na pilha. Portanto existe um caminho de w até um ancestral próprio de v, donde o arco v-w abraça v. Assim, a linha F aplica o segundo item da fórmula.

Exemplo D. Considere o grafo definido pelas listas de adjacência abaixo. Veja à direita uma floresta DFS do grafo.

Veja o rastreamento da execução da função GRAPHstrongCompsT(), com dfsR(v) representando dfsRstrongCompsT(G,v):

Na figura da floresta DFS à direita, cada vértice v é precedido do valor de pre[v] e seguido do valor de lo[v]. A figura mostra que as cabeças das componentes fortes são d, b, a.

Nas linhas do rastreamento que começam com um v dfsRstrongCompsT(v) ou um u-v dfsRstrongCompsT(v), a coluna stack dá o estado da pilha stack[0..t-1] no fim da linha A do código.

As linhas do rastreamento que têm apenas um v-w na primeira coluna representam o processamento do arco v-w pelo bloco de linhas E-G do código.

Cada linha do rastreamento que tem apenas um v (lo=i) na primeira coluna marca o fim do processamento do vértice v (fim da linha H do código). Nessa ocasião, i é o valor de lo[v]. A coluna stack dá o estado da pilha stack[0..t-1] no fim da execução de dfsRstrongCompsT(G,v,sc) e a coluna componentes dá os vértices da nova componente descoberta se lo[v] ≡ pre[v].

Ao fim da execução da função, os vetores pre[], lo[] e sc[] estarão no seguinte estado:

Exemplo E. Considere o grafo definido pelas listas de adjacência abaixo. Veja à direita uma floresta DFS do grafo.

Veja o rastreamento da execução da função GRAPHstrongCompsT(), com dfsR(v) representando dfsRstrongCompsT(G,v):

Na figura à direita, cada vértice v da floresta DFS é precedido do valor de pre[v] e seguido do valor de lo[v]. A figura mostra que as cabeças da componentes fortes são b, c, a. O vetor sc[] termina no seguinte estado:

Exemplo F. Considere a aplicação da função GRAPHstrongCompsT() ao grafo definido pelas listas de adjacência abaixo. Veja ao lado uma floresta DFS do grafo.

Segue o rastreamento da execução de GRAPHstrongCompsT(), com dfsR(v) representando dfsRstrongCompsT(G,v):

Na figura à direita, cada vértice v da floresta DFS é precedido de pre[v] e seguido de lo[v]. A figura mostra que as cabeças da componentes fortes são b, c, a. O vetor sc[] termina no seguinte estado:

Exemplo G. Considere a aplicação da função GRAPHstrongCompsT() ao grafo da figura. Para que o exemplo seja mais legível, usaremos os seguintes nomes alfabéticos alternativos para os vértices:

Veja a seguir o rastreamento da execução da função supondo que as listas de adjacência estão em ordem crescente dos nomes dos vértices.

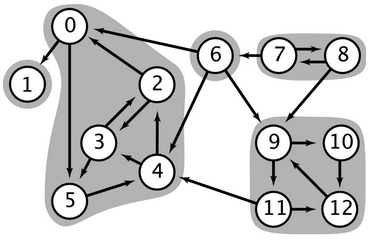
Na figura à direita, cada vértice v da floresta DFS é precedido de pre[v] e seguido de lo[v]. A figura mostra que as cabeças da componentes fortes são b, a, j, g, h. Veja uma representação das componentes fortes na figura que está no início deste capítulo. Os vetores pre[], lo[] e sc[] terminam no seguinte estado:

Exercícios 5

Prova da propriedade da pilha de vértices. Prove a propriedade da pilha de vértices.
Mostre que o teste pre[w] < pre[v] na linha E de dfsRstrongCompsT() pode ser eliminado em vista do teste pre[w] < lo[v] na linha F.
Mostre que o processo iterativo nas linhas J-K de dfsRstrongCompsT() não corre o risco de ultrapassar o fundo da pilha stack[0..t-1]. Em outras palavras, mostre que v está na pilha quando a linha I é executada.
Mostre que no início de cada nova etapa em GRAPHstrongCompsT() a pilha stack[0..t-1] está vazia (ou seja, t é igual a 0).
★ Instâncias extremas. A aplicação da função GRAPHstrongCompsT() a um grafo que tem apenas um vértice produz o resultado correto? E a aplicação a um grafo que não tem arcos? E a aplicação a um grafo fortemente conexo? Justique suas respostas diretamente a partir do código da função.
[Sedgewick 19.127] Aplique a função GRAPHstrongCompsT() ao grafo definido pelo conjunto de arcos 3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4. Faça o rastreamento da execução da função.
[Sedgewick 19.124] Caminho e ciclo. Aplique a função GRAPHstrongCompsT() ao grafo-caminho 0-1-2-3-4-5-6-7-8-9. Aplique a função GRAPHstrongCompsT() ao grafo-ciclo 0-1-2-3-4-5-6-7-8-9-0.
Aplique a função GRAPHstrongCompsT() ao trevo de 3 folhas definido pelos arcos 0-1 1-0 1-2 2-1 1-3 3-2. Faça o rastreamento da execução da função.
Aplique a função GRAPHstrongCompsT() a um dag. Explique o que acontece em cada linha do código da função.
Repita o exemplo G tomando os vértices em ordem decrescente de nomes e supondo que as listas de adjacência estão em ordem decrescente de nomes.

Variante Sedgewick da implementação. O Programa 19.11 do livro de Sedgewick escreve a função dfsRstrongCompsT() de maneira um pouco diferente (possivelmente baseada no Stanford GraphBase de Knuth). Analise essa implementação.

static void dfsRstrongCompsT( Graph G, vertex v, int *sc) {
   pre[v] = cnt++;
   stack[t++] = v;
   int min = pre[v];
   for (link a = G->adj[v]; a != NULL; a = a->next) {
      vertex w = a->w;
      if (pre[w] == -1)
         dfsRstrongCompsT( G, w, sc);
      if (lo[w] < min) min = lo[w];
   }
   lo[v] = min;
   if (lo[v] == pre[v]) {
      vertex u;
      do {
         u = stack[--t];
         sc[u] = k;
         lo[u] = G->V;
      } while (stack[t] != v); 
      k++;
   }
}

[Sedgewick 19.128] Versão para matriz de adjacências. Escreva uma versão de GRAPHstrongCompsT() para grafos representados por matriz de adjacências.
Versão iterativa. Escreva uma implementação não recursiva do algoritmo de Tarjan.
Um arco de um grafo é uma diponte se não pertence a um ciclo (e portanto suas pontas estão em componentes fortes distintas). Escreva uma função que imprima uma lista de todas as dipontes de um grafo.
Compare o código da função GRAPHstrongCompsT() com o da função GRAPHstrongT2(), que decide se um grafo é fortemente conexo. Quais as diferenças? Quais as semelhanças?

Desempenho

A função GRAPHstrongCompsT() consiste essencialmente em uma busca em profundidade. Assim, o consumo de tempo é proporcional a

no pior caso, sendo V o número de vértices e A o número de arcos do grafo. (Se A ≥ V, como acontece em muitas aplicações, podemos dizer que o consumo de tempo é proporcional a A.) O algoritmo é, portanto, linear no tamanho do grafo.

Exercícios 6

★ Testes. Escreva um programa para testar a função GRAPHstrongCompsT(). Use grafos aleatórios de vários tamanhos para fazer os testes. Compare os resultados de GRAPHstrongCompsT() com os resultados de um algoritmo ingênuo, como o sugerido no fim do capítulo Componentes fortes. (Um algoritmo ingênuo é fácil de programar corretamente e por isso é um ótimo padrão de referência durante a implementação e testes de algoritmos mais sofisticados.) Aproveite para cronometrar GRAPHstrongCompsT() e o algoritmo ingênuo.
★ Atualização da biblioteca. Acrescente GRAPHstrongCompsT() e dfsRstrongCompsT() à biblioteca GRAPHlists que mencionamos no capítulo Estruturas de dados para grafos. Faça alocação dinâmica dos vetores pre[], lo[] e stack[]. Também acrescente as versões apropriadas das funções à biblioteca GRAPHmatrix.
Numeração anti-topológica das componentes fortes. Depois de executar a função GRAPHstrongCompsT(), mostre que sc[] é uma numeração anti-topológica do grafo das componentes fortes de G.
Componente forte grande em torneio. Qual a probabilidade de que um torneio aleatório com V vértices tenha uma componente forte com mais que 0.9V vértices? Tente determinar essa probabilidade experimentalmente para V valendo 1000, 10000, e 100000.
Componente forte gigante. Como o número de vértices da maior componente forte de um grafo aleatório com V vértices e A arcos evolui em função de A (com V fixo)? Faça experimentos para responder essa pergunta. Cada experimento consiste em construir M grafos aleatórios (com V vértices e A arcos cada) e determinar (1) o tamanho médio da maior componente forte e (2) o número total de componentes fortes (se esse número for grande, o tamanho das demais componentes deve ser pequeno). Repita o experimento com A = a V log₁₀ V e a valendo 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 1, 2, 3, 4. Imprima uma tabela que mostre, para cada valor de A, o tamanho médio da maior componente forte e o número total médio de componentes fortes. O seu programa deve receber os valores de V e M pela linha de comando. Brinque com o programa variando M e V. Tente V igual a 1000, 5000 e 10000, por exemplo.
Componente forte gigante? Quantos arcos, pelo menos, um grafo aleatório com V vértices precisa ter para que apareça uma componente forte com mais que 0.9V vértices? Para cada valor de V no conjunto {1000, 5000, 10000}, use busca binária para determinar o menor número de arcos para o qual o grafo tem uma componente forte com mais que 0.9V vértices. (A busca binária consiste no seguinte: tente A igual à metade de V²−V; dependendo do resultado, tente A igual a um quarto de V²−V ou três quartos de V²−V, e assim por diante.) Para cada valor de V, repita o experimento algumas dezenas de vezes (variando a semente do gerador de números aleatórios) e calcule a média. Imprima uma tabela com os resultados.
Tamanhos das componentes fortes de grafos aleatórios. Quantos vértices (em média) tem cada componente forte de um grafo aleatório com V vértices e A arcos? Para cada valor fixo de V, como evolui o número médio de componentes de cada tamanho quando A aumenta? Faça experimentos para tentar responder essas perguntas. Cada experimento consiste em construir um grafo aleatório com V vértices e A arcos em média e determinar o número de componentes fortes de cada tamanho. (Aqui, tamanho é o número de vértices.) Para cada valor de V no conjunto {100, 1000, 10000}, faça os experimentos com A = a V log₁₀ V e a valendo 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 1, 2, 3, 4. Repita cada experimento algumas dezenas de vezes (variando a semente do gerador de números aleatórios) e calcule o número médio de componentes de cada tamanho. Imprima uma tabela para cada valor de V. Cada tabela deve ter uma coluna para cada valor de A.