Capítulo 9
Emparelhamentos perfeitos de custo mínimo
Agora que sabemos calcular
um emparelhamento
perfeito
(veja o capítulo 7)
num grafo não-dirigido,
podemos empreender o próximo passo:
calcular um emparelhamento perfeito
de custo mínimo.
Este capítulo
resolve o problema em grafos bipartidos
e faz um esboço da solução no caso geral.
As técnicas desenvolvidas para resolver o problema
estão na origem da chamada combinatória poliédrica,
que se tornou ferramenta essencial no estudo de muitos
problemas de otimização combinatória.
Todos os grafos neste capítulo
são não-dirigidos.
Por isso, diremos simplesmente grafo,
deixando subentendido o adjetivo não-dirigido.
Para conferir as definições de outros termos técnicos,
consulte o
índice remissivo
e os apêndices.
9.1 O problema
Seja $G$ um grafo
e $c$ uma função que atribui custos às arestas
de $G$.
(O custo de uma aresta pode ser positivo, negativo, ou nulo.)
Para qualquer conjunto $M$ de arestas,
denotaremos por $c(M)$ a soma $\sum_{e\in M} c_e$.
Problema 9.A (emparelhamento perfeito mínimo)
Dado um grafo
$G$ e uma função
$c$ que atribui um custo em $\R$
a cada aresta,
encontrar um emparelhamento perfeito $M$ que
minimize $c(M)$.
Usaremos as abreviaturas ep
e ep mínimo
para as expressões emparelhamento perfeito
e emparelhamento perfeito de custo mínimo
respectivamente.
(É razoável omitir a expressão de custo
pois mínimo
não poderia estar se referindo à cardinalidade do emparelhamento.)
Exemplo 9.1:
Considere o grafo definido pela
matriz de adjacências
abaixo.
Os custos das arestas são dados na tabela.
Há dois ep's,
sendo $\conj{ad,bc}$ o que tem custo mínimo.
\[
\begin{array}[t]{l@{\quad}*{4}{c}}
& a & b & c & d \\[0.5ex]
a & - & - & 1 & 1 \\
b & - & - & 1 & 1 \\
c & 1 & 1 & - & - \\
d & 1 & 1 & - & -
\end{array}
\qquad
\begin{array}[t]{l@{\quad}*{5}{r}}
& ac & ad & bc & bd \\[0.5ex]
\hline
c & +60 & +70 & -10 & +10
\end{array}
\]
Exercícios 9.1
-
Uma loja de aluguel de pranchas de surf
quer alugar $n$ pranchas para $n$ surfistas.
As pranchas têm comprimentos $l_1 \leq \cdots \leq l_n$ e
os surfistas têm alturas $h_1 \leq \cdots \leq h_n$.
Idealmente, o comprimento de uma prancha deve ser igual à altura do surfista.
Digamos que
um emparelhamento entre pranchas a surfistas é ótima
se minimiza a soma das diferenças, em o valor absoluto,
entre a altura do surfista e o comprimento de sua prancha.
Formule essa questão como um problema de ep mínimo.
Mostre que o emparelhamento $\conj{l_1h_1,\ldots,l_nh_n}$ é ótimo.
(Dica:
Mostre que se $l\leq l'$ e $h\leq h'$ então $|l-h|+|l'-h'| \leq |l-h'|+|l'-h|$.
Depois, faça a diferença simétrica entre dois ep's.)
-
Suponha dado um grafo com custos nas arestas.
Se multiplicarmos o custo de cada aresta por $100$,
é verdade que todo ep mínimo continua sendo mínimo?
Se somarmos $200$ ao custo de cada aresta,
é verdade que todo ep mínimo continua sendo mínimo?
-
★
Circuitos alternantes.
Seja $M$ um ep em um grafo com custos $c$ nas arestas.
O peso de qualquer circuito
alternante $C$
é o número $c(E(C)\setm M) - c(E(C)\cap M)$.
Prove que $M$ é um ep mínimo
se e somente se
o grafo não tem circuitos alternantes de peso negativo.
(Dica: considere
diferenças simétricas.)
[CCPS 5.35]
9.2 Um programa linear para ep mínimo
Para projetar um algoritmo para o problema 9.A,
é importante representar o problema
por meio de um programa linear.
Se $x$ é o vetor característico de um ep
num grafo $G$
então $x(\cut(v))=1$
para cada nó $v$ de $G$.
Portanto,
o problema do ep mínimo pode ser representado pelo seguinte programa linear:
encontrar um vetor real $(x_e : e\in E)$ que
\begin{equation}\label{lp:bipartite-min-cost-pm}
\begin{split}
\text{minimize} \quad cx & \\
\text{sob as restrições} \quad
x(\cut(v)) & \ = \ 1 \quad \text{para cada $v$ em $V$}\\
x_e & \ \geq \ 0 \quad \text{para cada $e$ em $E$,}
\end{split}
\end{equation}
sendo $V:=V(G)$ e
$E:=E(G)$.
É claro que toda
solução viável
inteira
(e portanto binária)
do pl
representa um ep.
Portanto, uma solução ótima
$x$ do pl representa uma solução
do problema 9.A
desde que $x$ seja inteiro.
Entretanto, muitas soluções ótimas do pl não são
inteiras.
[Se trocarmos
a restrição $x_e\geq 0$
por $x_e \in \conj{0,1}$
—
ou, alternativamente,
por $x_e\in \Zplus$
—
o programa \eqref{lp:bipartite-min-cost-pm}
representará corretamente o problema 9.A,
mas deixará de ser linear.]
(Compare \eqref{lp:bipartite-min-cost-pm} com o
pl $(1)$ do capítulo 4,
que trata de fluxo viável de custo mínimo em grafos dirigidos.
Lá, toda solução não-inteira
do pl é solução do problema do fluxo.)
Exemplo 9.2:
Seja $G$ um grafo completo
com nós $a$, $b$ e $c$
e o vetor de custos dado na tabela.
É claro que $G$ não tem ep algum.
Mas o vetor $x$ é solução ótima do pl \eqref{lp:bipartite-min-cost-pm}.
\[
\begin{array}[t]{l@{\quad}rrr}
& ab & bc & ca \\[0.5ex]
c & +10 & +10 & +10 \\
x & 0.5 & 0.5 & 0.5
\end{array}
\]
Exemplo 9.3:
Seja $G$ um grafo completo com conjunto nós $a$,
$b$, $c$ e $d$.
A tabela define o vetor $c$ de custos.
Também define soluções viáveis $x$ e $x'$
do pl \eqref{lp:bipartite-min-cost-pm}.
As soluções $x$ e $x'$ são ótimas,
mas apenas $x'$ representa um ep.
\[
\begin{array}[t]{r@{\quad}rrrrrr}
& ab & bc & cd & da & ac & bd \\[0.5ex]
c & +10 & +20 & +10 & +20 & +10 & +10 \\
x & 0.4 & 0 & 0.4 & 0 & 0.6 & 0.6 \\
x' & 1 & 0 & 1 & 0 & 0 & 0
\end{array}
\]
Exemplo 9.4:
Seja $G$ um grafo completo com conjunto nós $a$,
$b$, $c$ e $d$.
A tabela define o vetor de custos
e soluções viáveis $x$, $x'$,
$x''$ e $x'''$
do pl \eqref{lp:bipartite-min-cost-pm}.
Observe que $cx=20$, $cx'=19$,
$cx''=20$ e $cx'''=30$.
Apenas $x''$ e $x'''$ representam ep's, e nenhum deles é mínimo.
\[
\begin{array}[t]{r@{\quad}*{6}r}
& ab & bc & cd & da & ac & bd \\[0.5ex]
c & +10 & +5 & +10 & +5 & +15 & +15 \\
x & 1/3 & 1/3 & 1/3 & 1/3 & 1/3 & 1/3 \\
x' & 0.9 & 0.1 & 0.9 & 0.1 & 0 & 0 \\
x'' & 1 & 0 & 1 & 0 & 0 & 0 \\
x''' & 0 & 0 & 0 & 0 & 1 & 1
\end{array}
\]
Programa dual.
O dual do programa linear \eqref{lp:bipartite-min-cost-pm}
consiste em encontrar um vetor real $(y_v : v\in V)$ que
\begin{equation}\label{lp:dual:bipartite-min-cost-pm}
\begin{split}
\text{maximize} \quad y\,1 & \\
\text{sujeito a} \quad
y_v+y_w & \ \leq \ c_{vw} \quad \text{para cada $vw$ em $E$.}
\end{split}
\end{equation}
A expressão $y\,1$ denota a soma
$\sum_{v\in V} y_v$.
Diremos que um vetor $y$ que satisfaz as
restrições \eqref{lp:dual:bipartite-min-cost-pm} é um
potencial viável.
[Não confunda com o conceito de potencial viável
associado ao problema do caminho de custo mínimo
na seção 1.2.
Ao contrário daquele,
este potencial deixa de ser viável se somarmos
um mesmo número
a cada componente $y_v$.]
É fácil encontrar um potencial viável:
se $c_e \geq \alpha$ para toda aresta $e$
então o potencial
que atribui $\alpha/2$ a cada nó é viável.
Dado um potencial $y$,
o custo reduzido
de uma aresta $vw$ é o número $c_{vw}-y_v-y_w$.
O vetor de custos reduzidos será denotado
por $\cy$.
Portanto,
\[
\cy_{vw} := c_{vw} - y_v - y_w
\]
para cada aresta $vw$.
Observe que $\cy\geq 0$ se e somente se
o potencial $y$ é viável.
Como se sabe,
uma solução viável $x$ do pl \eqref{lp:bipartite-min-cost-pm}
é ótima se e somente se existe um potencial viável $y$
tal que $cx=y1$.
E essa igualdade vale se e somente se
as folgas de $x$ e $y$ são complementares,
isto é, se e somente se
\begin{equation}\label{eq:complementary-slackness-min-cost-pm-2}
x_e = 0 \quad \text{ou} \quad \cy_e = 0
\end{equation}
para todo $e$ em $E$.
Exemplo 9.5:
Considere o grafo completo com nós
$a$, $b$,
$c$, $d$.
As tabelas definem um vetor de custos $c$,
um potencial viável $y$,
o vetor $\cy$ de custos reduzidos,
e soluções viáveis $x$ e $x'$ do pl \eqref{lp:bipartite-min-cost-pm}.
\[
\begin{array}[t]{r@{\quad}*{6}r}
& ab & bc & cd & da & ac & bd \\[0.5ex]
c & +40 & +75 & +75 & +40 & +90 & +90 \\
\cy & 0 & 0 & 0 & 0 & 35 & 30 \\
x & 1 & 0 & 1 & 0 & 0 & 0 \\
x' & 0.5 & 0.5 & 0.5 & 0.5 & 0 & 0
\end{array}
\qquad\quad
\begin{array}[t]{l@{\quad}r}
& y \\[0.5ex]
a & +10 \\
b & +30 \\
c & +45 \\
d & +30
\end{array}
\]
As soluções viáveis $x$ e $y$ têm folgas complementares.
Portanto, $x$ é solução ótima do pl \eqref{lp:bipartite-min-cost-pm}.
Sendo binário, $x$ representa um ep mínimo.
As folgas das soluções viáveis $x'$ e $y$ também são complementares
e portanto $x'$ é solução ótima do pl \eqref{lp:bipartite-min-cost-pm}.
Mas $x'$ não representa um ep.
Como veremos na próxima seção,
o programa linear dual \eqref{lp:dual:bipartite-min-cost-pm}
e o conceito de potencial viável
têm um papel importante no projeto de um algoritmo
para o problema 9.A,
pelo menos quando o problema é restrito a grafos bipartidos.
Exercícios 9.2
-
Por que o pl \eqref{lp:bipartite-min-cost-pm}
não tem a restrição
$x_e\leq 1$ para cada $e\in E$
?
-
Mostre que todo ep corresponde a uma solução viável inteira do
pl \eqref{lp:bipartite-min-cost-pm}.
Mostre que toda solução viável inteira do pl \eqref{lp:bipartite-min-cost-pm}
corresponde a um ep.
-
★
Escreva explicitamente os pl's \eqref{lp:bipartite-min-cost-pm}
e \eqref{lp:dual:bipartite-min-cost-pm}
para o grafo definidos pelas tabelas abaixo.
\[
\begin{array}[t]{l@{\quad}cccc}
& a & b & c & d \\[0.2ex]
a & - & 1 & 1 & - \\
b & 1 & - & 1 & - \\
c & 1 & 1 & - & 1 \\
d & - & - & 1 & -
\end{array}
\qquad
\begin{array}[t]{l@{\quad}rrrrr}
& ab & bc & ca & cd \\[0.2ex]
c & +10 & +20 & +30 & +40
\end{array}
\]
-
Mostre que o pl \eqref{lp:dual:bipartite-min-cost-pm}
é o dual do pl \eqref{lp:bipartite-min-cost-pm}.
Prove que a condição de
folgas complementares \eqref{eq:complementary-slackness-min-cost-pm-2}
está correta.
-
Exiba uma instância
inviável do pl \eqref{lp:bipartite-min-cost-pm}
e uma instância inviável do pl \eqref{lp:dual:bipartite-min-cost-pm}.
-
Seja $G$ um grafo completo com $n$ nós.
Suponha que toda aresta tem custo $-10$.
Exiba um ep de custo mínimo.
Exiba uma solução ótima $x$ do pl \eqref{lp:bipartite-min-cost-pm}
e uma solução ótima $y$ do pl \eqref{lp:dual:bipartite-min-cost-pm}.
-
★
Seja $G$ um grafo bipartido
e suponha que o custo de cada aresta $vw$ é $b_v+b_w$,
sendo $b$ uma atribuição de números reais aos nós de $G$.
Descreva um bom algoritmo
para calcular um ep mínimo nesse caso.
Em seguida, descreva um algoritmo particularmente rápido
para o caso em que $G$ é bipartido completo.
[AMO 12.22b]
9.3 Algoritmo para ep mínimo em grafo bipartido
Seja $(G,c)$ uma instância
do problema 9.A
e considere a correspondente instância do
pl \eqref{lp:bipartite-min-cost-pm}.
Seja $y$ um potencial viável
e $\cy$ o correspondente custo reduzido.
Dizemos que uma aresta $e$ de $G$ está justa
se $\cy_e=0$.
O conjunto das arestas justas
será denotado por $\Eequ$
e às vezes denominado conjunto justo
.
A seguinte observação é o ponto de partida do projeto
de um algoritmo para o problema 9.A.
Dado um potencial viavel $y$ e um ep $M$ em $G$, se
\begin{equation}\label{eq:matching-subseteq-equality-set}
M \subseteq \Eequ
\end{equation}
então as folgas de $y$ e do vetor característico de $M$ são complementares,
ou seja, satisfazem \eqref{eq:complementary-slackness-min-cost-pm-2},
e portanto $M$ é um ep mínimo.
Assim,
para encontrar um ep mínimo em $(G,c)$,
basta encontrar um potencial viável $y$ e um ep no
subgrafo gerador justo $(V(G),\Eequ)$.
Se $G$ for bipartido, um tal par $(y,M)$ existe.
(Para uma prova não algorítmica desse fato,
veja o teorema de Birkhoff
no capítulo 10.)
Preliminares.
A procura por um ep no grafo $(V(G),\Eequ)$
pode ser executada pelo algoritmo EmpBipartidoPerfeito
da seção 7.4.
Por isso,
convém resumir alguns dos conceitos introduzidos
na seção 7.3.
Suponha que $M$ é um emparelhamento
num grafo $G$
e $T$ é uma árvore
$M$-alternante
com raiz $r$.
Um nó $v$ de $T$ é branco
se a distância de $r$ a $v$ em $T$ é ímpar,
e preto se essa distância é par.
A árvore $T$ é frustrada
se toda aresta de $G$ com uma ponta preta tem a outra ponta branca.
O lema 7.5 mostra que
se $T$ é frustrada então $G$ não tem um ep.
Os nós de $G$ que não pertencem a $T$ têm cores:
um nó $w$ é vermelho se estiver
$M$-exposto
e verde em caso contrário.
Uma aresta
é preto-vermelha se uma de suas pontas é preta e a outra é vermelha.
Arestas preto-verde, preto-branca
e preto-preta são definidas analogamente.
Se $G$ é bipartido,
não tem circuitos ímpares
e portanto não tem arestas preto-pretas,
como observamos na seção 7.3.
O algoritmo húngaro.
O algoritmo que resolve a restrição do
problema 9.A
a grafos bipartidos foi proposto
por H. Kuhn
(1955)
e J. Munkers
(1957)
e ficou conhecido como
algoritmo húngaro.
O algoritmo
recebe um grafo bipartido $G$ e um vetor $c$ de custos
e devolve um ep de custo mínimo ou informa que $G$ não tem ep algum.
O algoritmo é iterativo.
Numa descrição grosseira e imprecisa,
poderíamos dizer que cada iteração começa com um potencial viável $y$
e usa o algoritmo EmpBipartidoPerfeito
para procurar um ep no grafo justo $\Gequ := (V(G),\Eequ)$.
Se um tal ep for encontrado,
o problema está resolvido graças a \eqref{eq:matching-subseteq-equality-set}.
Senão, $y$ é ajustado e uma nova iteração começa com o novo potencial viável.
Numa descrição mais precisa,
cada iteração começa com um potencial viável $y$
e um emparelhamento $M \subseteq \Eequ$.
(Na primeira iteração, $y$ é um potencial viável arbitrário.)
Se $M$ é perfeito,
o problema está resolvido.
Suponha agora que $M$ não é perfeito.
Então um código análogo ao de EmpBipartidoPerfeito
é usado para calcular uma árvore $M$-alternante $T$ em $\Gequ$.
Se $T$ levar a um caminho aumentador,
começamos uma nova iteração com um emparelhamento maior.
Caso contrário, $T$ é frustrada
em $\Gequ$.
Nesse caso, a árvore frustrada é usada como guia para
ajustar o potencial viável $y$.
O ajuste de $y$ é feito da seguinte maneira.
Seja $F$ o conjunto das arestas preto-verdes de $G$
e $F'$ o conjunto das arestas preto-vermelhas de $G$.
(É claro que $F\cup F'$ é disjunto de $\Eequ$.)
Se $F\cup F'$ é vazio então
toda aresta de $G$ com uma ponta preta tem a outra branca,
donde $T$ é frustrada em $G$,
e assim $G$ não tem ep algum.
Suponha agora que $F\cup F'$ não é vazio.
Seja $\epsilon$ o menor custo reduzido
dentre as arestas de $F\cup F'$,
isto é, $\epsilon := \min\left(\cy_{vw} : vw\in F\cup F'\right)$.
Um novo potencial é calculado da seguinte maneira:
para cada nó $v$ de $T$,
-
adicione $\epsilon$ a $y_v$ se $v$ é preto e
-
subtraia $\epsilon$ de $y_v$ se $v$ é branco.
O novo potencial é viável
(veja o exercício abaixo).
Uma nova iteração começa com esse novo potencial.
O novo conjunto justo pode não ser um superconjunto do anterior.
Ainda assim, o novo conjunto justo
contém $M$ e $E(T)$.
Ademais, o novo conjunto justo contém alguma aresta
de $F\cup F'$,
uma vez que $\epsilon > 0$.
Uma nova iteração começa com o novo valor de $y$
e com o emparelhamento $M$ da iteração anterior.
Como se vê, o algoritmo avança ajustando
o potencial viável $y$
e, ao mesmo tempo,
o emparelhamento $M$.
Esse tipo de algoritmo é conhecido como primal-dual
e aparece frequentemente em otimização combinatória.
Exemplo 9.6
[CCPS fig.5.12]:
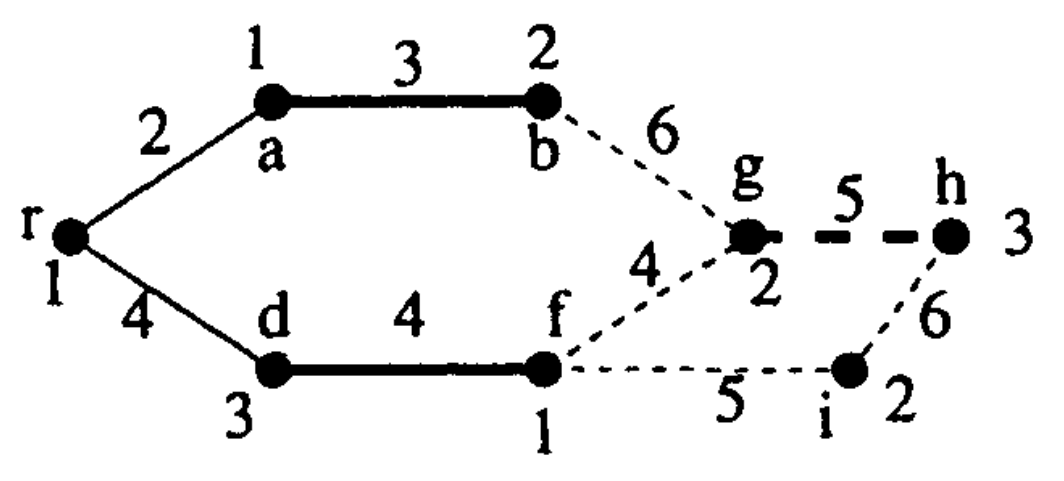
A figura mostra um grafo $G$
com custos nas arestas.
A primeira coluna da tabela define um potencial viável $y$.
O conjunto de arestas justas é $\Eequ=\conj{ra, ab, rd, df, gh}$.
O algoritmo húngaro começa com o emparelhamento
$M:=\conj{ab,df,gh}$
representado pelas linhas grossas da figura.
A primeira iteração do algoritmo
procura um ep no subgrafo justo $(V,\Eequ)$.
Para isso, constrói a árvore $M$-alternante $T$
com raiz $r$
e arestas $ra$, $ab$,
$rd$ e $df$
(linha sólidas
da figura).
Os nós $r$, $b$ e $f$ são pretos e os nós $a$ e $d$ são brancos.
Os nós $g$ e $h$ são verdes e o nó $i$ é vermelho.
Não há arestas preto-verdes nem preto-vermelhas no subgrafo justo.
A árvore $T$ é frustrada no subgrafo justo
e portanto o subgrafo não tem ep.
\[
\begin{array}[t]{l@{\quad}r}
& y \\[0.5ex]
r & +1 \\
a & +1 \\
b & +2 \\
d & +3 \\
f & +1 \\
g & +2 \\
h & +3 \\
i & +2
\end{array}
\hspace{6ex}
\begin{array}[t]{l@{\enspace}*{9}c}
& ra & ab & rd & df & bg & fg & gh & fi & hi \\[0.5ex]
\cy & 0 & 0 & 0 & 0 & 2 & 1 & 0 & 2 & 1
\end{array}
\]
Em $G$, o conjunto das arestas preto-verdes e preto-vermelhas
é $F\cup F' :=\conj{bg, fg, fi}$.
O menor custo reduzido nesse conjunto é $\epsilon:=1$.
Um novo potencial é calculado
somando $\epsilon$ ao potencial de cada nó preto
e subtraindo $\epsilon$ do potencial de cada nó branco.
Esse segundo potencial é viável.
A aresta $fg$ fica justa e portanto pertence ao novo $\Eequ$.
\[
\begin{array}[t]{l@{\quad}r}
& y \\[0.5ex]
r & +2 \\
a & 0 \\
b & +3 \\
d & +2 \\
f & +2 \\
g & +2 \\
h & +3 \\
i & +2
\end{array}
\hspace{6ex}
\begin{array}[t]{l@{\enspace}*{9}c}
& ra & ab & rd & df & bg & fg & gh & fi & hi \\[0.5ex]
\cy & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1
\end{array}
\]
Na segunda iteração, a árvore $T$ continua crescendo no novo subgrafo justo.
As arestas $fg$ e $gh$ são acrescentadas a $T$.
Essa árvore é frustrada (no subgrafo justo)
e portanto o subgrafo não tem ep.
Em $G$, o conjunto das arestas preto-verdes e preto-vermelhas
é $F\cup F' :=\conj{fi, hi}$.
O menor custo reduzido nesse conjunto é $\epsilon:=1$.
Um novo potencial viável é calculado
somando $\epsilon$ ao potencial de cada nó preto
e subtraindo $\epsilon$ do potencial de cada nó branco.
As arestas $fi$ e $hi$ tornam-se justas.
\[
\begin{array}[t]{l@{\quad}r}
& y \\[0.5ex]
r & +3 \\
a & -1 \\
b & +4 \\
d & +1 \\
f & +3 \\
g & +1 \\
h & +4 \\
i & +2
\end{array}
\hspace{6ex}
\begin{array}[t]{l@{\enspace}*{9}c}
& ra & ab & rd & df & bg & fg & gh & fi & hi \\[0.5ex]
\cy & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0
\end{array}
\]
Na terceira iteração,
a árvore $T$ continua crescendo no (novo) subgrafo justo.
A aresta $hi$ é acrescentada a $T$.
O caminho $(r,d,f,g,h,i)$ em $T$ é aumentador.
Depois que esse caminho aumentador for processado
teremos um ep no subgrafo justo $(V,\Eequ)$.
Esse ep é mínimo em $G$.
Veja
o rastreamento da execução do algoritmo.
Cada linha da tabela descreve os valores das variáveis
ao longo de uma iteração:
\[
\begin{array}{rrrrrrrrc*{5}{l@{\quad}}}
%%% & & & y \ \\
y_r& y_a& y_b& y_d& y_f& y_g& y_h& y_i &&
\Eequ &&
M \subseteq \Eequ&&
T &&
F\cup F' &&
\epsilon & \\[0.5ex]
\hline\rule{0ex}{2.5ex}
1& 1& 2& 3& 1& 2& 3& 2 &&
ra\ ab\ rd\ df\ gh &&
ab\ df\ gh &&
rab\ \ rdf &&
bg\ fg\ fi &&
1\\
2& 0& 3& 2& 2& 2& 3 & 2 &&
\text{mais} \ fg &&
ab\ df\ gh &&
\text{mais} \ fgh\ \ hi &&
fi\ hi &&
1\\
3& -1& 4& 1& 3& 1& 4& 2 &&
\text{mais} \ fi\ hi &&
ab\ rd\ fg\ hi
\end{array}
\]
Segue o código do algoritmo húngaro:
|
Húngaro $(G, c)$
|
|
01
.
seja $y$ um potencial viável
|
|
02
.
seja $M\subseteq \Eequ$ um emparelhamento em $G$
|
|
03
.
enquanto o emparelhamento $M$ não é perfeito faça
|
|
04
.ooo
seja $r$ um nó $M$-exposto
|
|
05
.ooo
$T \larr (\conj{r},\emptyset)$
|
|
06
.ooo
repita
|
|
07
.oooooo
enquanto existe aresta preto-verde em $\Eequ$ faça
|
|
08
.ooooooooo
seja $vw$ uma aresta preto-verde em $\Eequ$
|
|
09
.ooooooooo
$T \larr \text{}$ EstendeÁrvore $(G,M,T,vw)$
|
|
10
.oooooo
se não existe aresta preto-vermelha em $\Eequ$
|
|
11
.ooooooooo
então seja $F$ o conjunto das arestas preto-verdes de $G$
|
|
12
.ooooooooo
então seja $F'$ o conjunto das arestas preto-vermelhas de $G$
|
|
13
.ooooooooo
então se $F\cup F'=\emptyset$
|
|
14
.oooooooooooo
então então seja $A$ o conjunto dos nós brancos de $T$
|
|
15
.oooooooooooo
então então devolva $A$ e pare
|
|
16
.ooooooooo
então $\epsilon \larr \min\left(c_{vw}-y_v-y_w : vw\in F\cup F'\right)$
|
|
17
.ooooooooo
então $y_v\larr y_v+\epsilon$ para cada $v$ preto
|
|
18
.ooooooooo
então $y_v\larr y_v-\epsilon$ para cada $v$ branco
|
|
19
.ooooooooo
senão seja $vw$ uma aresta preto-vermelha em $\Eequ$
|
|
20
.ooooooooo
senão $M \larr \text{}$ AumentaEmp $(G,M,T,vw)$
|
21
.ooooooooo
senão interrompa o repita da linha 06
|
|
22
.
devolva $M$ e $y$ e pare
|
Exceto pelas linhas 11 a 13 e 16 a 18,
o código é essencialmente igual ao do
algoritmo EmpBipartidoPerfeito
da seção 7.4.
O processo iterativo externo, que ocupa as linhas 03 a 21,
procura um ep no conjunto justo $\Eequ$.
No início de cada iteração desse processo
temos um potencial viável $y$ e um emparelhamento $M\subseteq \Eequ$.
O processo iterativo interno, que ocupa as linhas 06 a 21,
recebe um emparelhamento imperfeito $M$
e procura um caminho $M$-aumentador no subgrafo justo.
No início de cada iteração desse processo,
temos não só um potencial viável $y$
e um emparelhamento imperfeito
$M\subseteq \Eequ$,
como também uma árvore $M$-alternante $T$
com $E(T)\subseteq \Eequ$.
O algoritmo pode alterar $y$ durante a iteração,
mas as propriedades $M\subseteq \Eequ$ e $E(T)\subseteq \Eequ$
são preservadas e pelo menos uma nova aresta torna-se justa.
Na linha 15, temos $\oc_1(G{-}A) > |A|$.
A existência de um tal $A$ prova que $G$ não tem ep,
conforme o
lema 7.2.
Exemplo 9.7:
Considere o grafo bipartido definido pela matriz de adjacências abaixo.
À direita da matriz temos
os custos das arestas.
\[
\begin{array}[t]{lcccc}
& a & b & c & d \\[0.5ex]
a & - & - & 1 & 1 \\
b & - & - & 1 & 1 \\
c & 1 & 1 & - & - \\
d & 1 & 1 & - & -
\end{array}
\hspace{6ex}
\begin{array}[t]{lrrrr}
& ac & ad & bc & bd \\[0.5ex]
\hline
c \he & 90 & 40 & 75 & 95
\end{array}
\]
Comece a execução do algoritmo Húngaro
com o potencial viável $y$
dado abaixo.
Esse potencial determina o custo reduzido $\cy$
e o subgrafo justo $\Gequ$ cuja matriz aparece abaixo.
A tabela dá o vetor característico $x$
do emparelhamento $M$ escolhido na linha 02 do algoritmo.
\[
\begin{array}[t]{l@{\quad}r}
& y \\[0.5ex]
a & 20 \\
b & 0 \\
c & 70 \\
d & 15
\end{array}
\hspace{6ex}
\begin{array}[t]{lrrrr}
& ac & ad & bc & bd \\[0.5ex]
\cy & 0 & 5 & 5 & 80 \\
x & 1 & 0 & 0 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{l@{\quad}cccc}
& a & b & c & d \\[0.5ex]
a & - & - & 1 & - \\
b & - & - & - & - \\
c & 1 & - & - & - \\
d & - & - & - & -
\end{array}
\]
A primeira iteração chega à linha 11 com $T=(\conj{b},\emptyset)$.
Nas linhas 11 a 18,
calcula $\epsilon=5$ e altera $y$,
tornando justa a aresta $bc$.
Veja os novos valores das variáveis:
\[
\begin{array}[t]{l@{\quad}r}
& y \\[0.5ex]
a & 20 \\
b & 5 \\
c & 70 \\
d & 15
\end{array}
\hspace{6ex}
\begin{array}[t]{lrrrr}
& ac & ad & bc & bd \\[0.5ex]
\cy & 0 & 5 & 0 & 75 \\
x & 1 & 0 & 0 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{lcccc}
& a & b & c & d \\[0.5ex]
a & - & - & 1 & - \\
b & - & - & 1 & - \\
c & 1 & 1 & - & - \\
d & - & - & - & -
\end{array}
\]
A segunda iteração acrescenta as arestas $bc$ e $ca$ à arvore $T$.
Em seguida, calcula $\epsilon=5$ e altera $y$,
tornando justa a aresta $ad$.
Veja os novos valores das variáveis:
\[
\begin{array}[t]{lr}
& y \\[0.5ex]
a & 25 \\
b & 10 \\
c & 65 \\
d & 15
\end{array}
\hspace{5ex}
\begin{array}[t]{lrrrr}
& ac & ad & bc & bd \\[0.5ex]
\cy & 0 & 0 & 0 & 70 \\
x & 1 & 0 & 0 & 0
\end{array}
\hspace{5ex}
\begin{array}[t]{lcccc}
& a & b & c & d \\[0.5ex]
a & - & - & 1 & 1 \\
b & - & - & 1 & - \\
c & 1 & 1 & - & - \\
d & 1 & - & - & -
\end{array}
\]
A terceira iteração encontra o caminho aumentador $(b,c,a,d)$ no subgrafo justo.
Isso leva ao novo emparelhamento indicado abaixo.
O novo emparelhamento é perfeito e todas as arestas estão justas.
De acordo com \eqref{eq:matching-subseteq-equality-set},
o ep é mínimo em $G$.
\[
\ph{
\begin{array}[t]{lr}
& y \\[0.5ex]
a & 25 \\
b & 10
\end{array}
}
\hspace{6ex}
\begin{array}[t]{lrrrr}
& ac & ad & bc & bd \\[0.5ex]
\cy \hd & 0 & 0 & 0 & 70 \\
x \hd & 0 & 1 & 1 & 0
\end{array}
\qquad
\ph{
\begin{array}[t]{l@{\quad}cccc}
& a & b & c & d \\[0.5ex]
a & - & - & 1 & 1 \\
b & - & - & 1 & -
\end{array}
}
\]
Veja um resumo do rastreamento da execução do algoritmo.
Cada linha da tabela descreve os valores das variáveis
ao longo de uma iteração:
\[
\begin{array}{rrrrc*{5}{l@{\quad}}}
y_a& y_b& y_c& y_d &&
\Eequ &&
M \subseteq \Eequ&&
T &&
F\cup F' &&
\epsilon\\[0.5ex]
\hline\rule{0ex}{2.5ex}
20& 0& 70& 15 &&
ac &&
ac &&
b &&
bc\ bd &&
5\\
20& 5& 70& 15&&
ac\ bc &&
ac &&
bca &&
bd\ ad &&
5\\
25& 10& 65& 15&&
ac\ bc\ ad &&
bc\ ad
\end{array}
\]
Desempenho.
No pior caso, o algoritmo Húngaro
consome $\Oh(m n^2)$ unidades de tempo,
sendo $m$ o número de arestas e $n$ o número de nós do grafo.
O termo $m$
é consequência do processo iterativo externo,
que acrescenta pelo menos uma aresta a $\Gequ$ a cada iteração.
O termo $n^2$
representa o consumo de tempo
do algoritmo EmpBipartidoPerfeito.
Exercícios 9.3
-
Considere a seguinte afirmação:
Todo grafo bipartido com custos nas arestas tem um ep cujo custo
é igual ao valor ótimo do pl \eqref{lp:bipartite-min-cost-pm}.
O que há de errado?
-
★
Suponha que o grafo $G$ tem bipartição $(P,Q)$.
Para calcular um potencial viável na linha 01 do algoritmo Húngaro,
comece por fazer $y_p:=0$ para todo $p$ em $P$.
Desenvolva essa ideia.
-
★
Mostre que o novo potencial calculado pelo algoritmo Húngaro
nas linhas 11 a 18 é viável.
Em seguida, mostre que o conjunto justo para o novo potencial
inclui $M$ e $E(T)$.
-
Seja $G$ o grafo bipartido completo
com bipartição $(\conj{a,b},\conj{c,d})$.
O vetor $c$ de custos é dado abaixo.
Calcule um ep mínimo em $(G,c)$.
Comece com o potencial $y$ e o emparelhamento $M=\conj{ac}$.
Antes, verifique que o potencial $y$ é viável.
\[
\begin{array}[t]{l@{\quad}*{4}{r}}
& ac & ad & bc & bd \\[0.5ex]
c & 10 & 50 & 30 & 30
\end{array}
\qquad
\begin{array}[t]{l@{\quad}*{1}{r}}
& y \\[0.5ex]
a & 0 \\
b & 2 \\
c & 1 \\
d & 4
\end{array}
\]
-
Calcule um ep mínimo no grafo bipartido completo
com bipartição $(\conj{a,b,c},\conj{d,e,f})$
que tem os custos indicados abaixo.
Procure escolher o potencial inicial $y$
de modo que o subgrafo justo $\Gequ$ tenha muitas arestas.
\[
\begin{array}[t]{l@{\quad}*{9}{r}}
& ad & ae & af & bd & be & bf & cd & ce & cf \\[0.5ex]
c & 20 & 10 & 50 & 40 & 30 & 30 & 50 & 40 & 20
\end{array}
\]
9.4 Um programa linear mais poderoso
O programa linear \eqref{lp:bipartite-min-cost-pm}
representa mal o problema 9.A,
a menos que o grafo seja bipartido.
Tipicamente,
o custo $c(M)$ de um ep mínimo $M$ é estritamente maior
que o custo $cx$ de uma solução ótima $x$ do pl,
e a correspodente solução $x$ não é inteira.
Precisamos de um pl mais poderoso
,
com restrições lineares que cortem fora
as soluções não-inteiras do pl \eqref{lp:bipartite-min-cost-pm}.
A ideia de acrescentar restrições lineares a um pl
para eliminar soluções fracionárias indesejadas
é muito efetiva e mostrou-se útil
em muitos problemas de otimização combinatória.
Dizemos que um corte $\cut(S)$
num grafo $G$ tem margem ímpar
se $|S|$ é ímpar.
(A paridade de $|\cut(S)|$ é irrelevante.)
Denotaremos por $\Fcal$ o conjunto de todos os subconjuntos $S$ de $V(G)$
tais que $|S|$ é ímpar.
Se $S \in \Fcal$ e
$x$ é o vetor característico de um ep então é claro que
\begin{equation}\label{eq:blossom-inequality}
x(\cut(S)) \geq 1\text{.}
\end{equation}
Portanto, podemos acrescentar essas desigualdades
ao pl \eqref{lp:bipartite-min-cost-pm}.
O resultado é o seguinte pl:
\begin{equation}\label{lp:min-cost-pm}
\begin{split}
\text{minimize} \quad cx & \\
\text{sujeito a} \quad
x(\cut(v)) & \ = \ 1 \quad \text{para cada $v$ em $V$}\\
x(\cut(S)) & \ \geq \ 1 \quad \text{para cada $S$ em $\Fcal$}\\
x_e & \ \geq \ 0 \quad \text{para cada $e$ em $E$.}
\end{split}
\end{equation}
As restrições $x(\cut(S))\geq 1$
são conhecidas como
desigualdades florais
(= blossom inequalities).
O número de desigualdades florais é enorme
pois o conjunto $\Fcal$ é enorme.
É bem verdade que algumas dessas desigualdades são claramente redundates.
Em primeiro lugar, se $|S|=1$ então a restrição $x(\cut(S))\geq 1$
está subentendida em $x(\cut(v))=1$.
O mesmo acontece se $|\compl{S}|=1$,
sendo $\compl{S} = V\setm S$.
Em segundo lugar,
se $|S|$ e $|\compl{S}|$ são ímpares
então as restrições $x(\cut(S))\geq 1$ e $x(\cut(\compl{S}))\geq 1$
são idênticas e portanto uma pode ser eliminada.
Mas a eliminação dessas redundâncias óbvias
não leva a uma redução significativa
do número de desigualdades florais.
Em cada instância específica do pl \eqref{lp:min-cost-pm},
a grande maioria das desigualdades florais se revela redundante
por razões que não são óbvias.
A dificuldade está em saber quais desigualdades florais
poderiam ser ignoradas.
Programa dual.
O pl dual de \eqref{lp:min-cost-pm}
tem uma variável $y_v$ para cada nó $v$
e uma variável $Y_S$ para cada $S$ em $\Fcal$
e consiste em encontrar um par $(y,Y)$ que
\begin{equation}\label{lp:dual:min-cost-pm}
\begin{split}
\text{maximize} \quad \textstyle
y1 + Y1 & \\[0.5ex]
\text{sujeito a} \quad
\textstyle y_v+y_w + \sum (Y_S : S\in \Fcal_{vw}) & \ \leq \ c_{vw} \quad
\text{para cada $vw$ em $E$}\\
Y_S & \ \geq \ 0 \quad
\text{para cada $S$ em $\Fcal$,}
\end{split}
\end{equation}
sendo $y1 = \sum_{v\in V} y_v\,$,
$Y1 = \sum_{S\in \Fcal} Y_S$ e
$\Fcal_{vw} := \conj{S \in \Fcal : \cut(S)\ni vw}$.
Dado um par $(y,Y)$,
o custo reduzido
de qualquer aresta $vw$ é o número $\cyY_{vw}$ definido assim:
\[\textstyle
\cyY_{vw} := c_{vw} - y_v - y_w - \sum (Y_S : S\in \Fcal_{vw})\text{.}
\]
Portanto, $(y,Y)$ é viável em \eqref{lp:dual:min-cost-pm}
se e somente se $\cyY_e\geq 0$ para cada $e$ em $E$
e $Y_S\geq 0$ para cada $S$ em $\Fcal$.
Folgas complementares.
Para qualquer solução viável $x$ do
pl \eqref{lp:min-cost-pm}
e qualquer solução viável $(y,Y)$ do
pl \eqref{lp:dual:min-cost-pm},
temos $cx=y1+Y1$ se e somente se
valem as seguintes folgas complementares:
para cada $e$ em $E$,
\[
x_e = 0 \quad \text{ou} \quad \cyY_e = 0
\]
e, para cada $S$ em $\Fcal$,
\[
x(S) = 1 \quad \text{ou} \quad Y_S = 0\text{.}
\]
Dada uma solução viável $(y,Y)$ do pl dual \eqref{lp:dual:min-cost-pm},
as condições de folgas complementares têm a seguinte consequência:
se $M$ é um ep tal que
$M \subseteq \EequY$ e $|M\cap S| = 1$
para cada $S$ em $\Fcal$ tal que $Y_S > 0$
então $M$ é um ep mínimo.
Laminaridade.
Em geral, numa solução ótima $(y,Y)$ de \eqref{lp:dual:min-cost-pm},
a maior parte das componentes de $Y$ é nula.
Ademais,
os conjuntos $S$ para os quais $Y_S>0$
formam uma coleção laminar
(veja a
seção A.5 do apêndice A)
e portanto há menos que $2|V|$ deles.
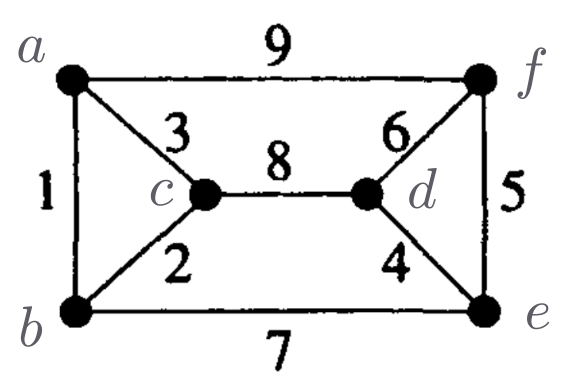
Exemplo 9.8
[CCPS fig.5.13]:
Para a instância do problema 9.A
descrita a seguir,
uma solução ótima do pl \eqref{lp:bipartite-min-cost-pm}
não define um ep.
\[
\begin{array}[t]{l@{\quad}cccccc}
& a & b & c & d & e & f \\[0.5ex]
a & - & 1 & 1 & - & - & 1 \\
b & 1 & - & 1 & - & 1 & - \\
c & 1 & 1 & - & 1 & - & - \\
d & - & - & 1 & - & 1 & 1 \\
e & - & 1 & - & 1 & - & 1 \\
f & 1 & - & - & 1 & 1 & -
\end{array}
\]
Considere então os pl's \eqref{lp:min-cost-pm}
e \eqref{lp:dual:min-cost-pm}.
Uma solução viável $x$ do pl \eqref{lp:min-cost-pm}
e uma solução viável $(y,Y)$ do
pl dual \eqref{lp:dual:min-cost-pm}
estão indicadas abaixo,
juntamente com o custo reduzido $\cyY$.
O vetor dual $Y$ tem uma única componente não nula:
$Y_S>0$ apenas quando
$S = \conj{a,b,c}$.
(São nulas, por exemplo, as componentes de $Y$ que correspondem
aos conjuntos $\conj{a,d,f}$,
$\conj{a,c,f}$ e $\conj{a,c,d}$.)
\[
\begin{array}[t]{r@{\quad}*{9}{c}}
& ab & bc & ca & de & ef & fd & be & cd & af \\[0.5ex]
c & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\
x & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\
\cyY & 0 & 0 & 0 & 1 & 0 & 2 & 0 & 0 & 0
\end{array}
\hspace{4ex}
\begin{array}[t]{r@{\quad}*{1}{r}}
& y \\[0.5ex]
a & 1 \\
b & 0 \\
c & 2 \\
d & 1 \\
e & 2 \\
f & 3
\end{array}
\hspace{4ex}
\begin{array}[t]{r@{\ }*{1}{r}}
& Y \\[0.2ex]
abc & 5
\end{array}
\]
Com um pouco de paciência, verificamos que
os valores $\cyY$ na tabela estão corretos e são não-negativos.
Tomando $M:=\conj{e : x_e=1}$,
constatamos que $M$ é um ep
e $M \subseteq \EequY$.
Além disso, $|M\cap \cut(S)| = 1$.
Portanto, $x$ e $(y,Y)$ têm folgas complementares.
Logo, $M$ é um ep mínimo.
Por curiosidade, verificamos ainda que
$cx = 14 = y1 + Y1$.
Veja outro potencial $(y,Y)$ que tem folgas complementares com as de $x$:
\[
\begin{array}[t]{r@{\quad}*{9}{c}}
& ab & bc & ca & de & ef & fd & be & cd & af \\[0.5ex]
c & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\
x & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\
\cyY & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 1
\end{array}
\qquad
\begin{array}[t]{r@{\quad}*{1}{l}}
& y \\[0.5ex]
a & 1 \\
b & 0 \\
c & 2 \\
d & 2.5 \\
e & 1.5 \\
f & 3.5
\end{array}
\qquad
\begin{array}[t]{r@{\enspace}*{1}{l}}
& Y \\[0.2ex]
abc & 3.5
\end{array}
\]
Exercícios 9.4
-
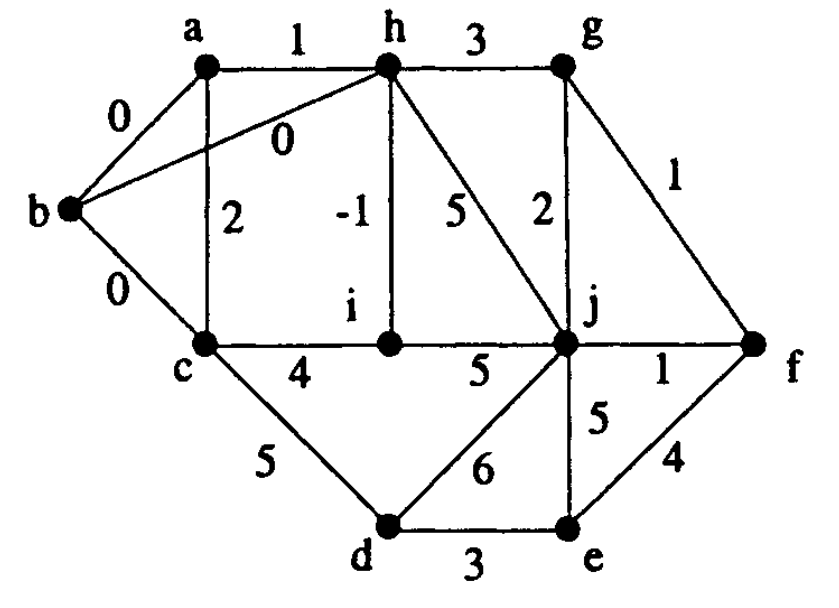
Faça uma lista de todos os conjuntos ímpares de nós do grafo abaixo.
Escreva cada conjunto ímpar ao lado do seu complemento (que também é ímpar).
Para cada conjunto ímpar $S$,
escreva a lista dos elementos de $\cut(S)$.
-
Seja $M$ um ep em um grafo $G$.
Seja $S$ um corte de margem ímpar.
Mostre que $M\cap S$ não é vazio.
-
No pl \eqref{lp:min-cost-pm},
é suficiente restringir as desigualdades florais aos
circuitos ímpares?
Ou seja, é suficiente supor que $\Fcal$ é a conjunto de
todos os cortes $\cut(S)$ tais que $S$ é o conjuntos de nós
de algum circuito ímpar?
-
Mostre que o pl \eqref{lp:dual:min-cost-pm}
é o dual do pl \eqref{lp:min-cost-pm}.
Verifique as condições de folgas complementares
dadas no texto acima.
-
Suponha que $G$ é um grafo com número ímpar de nós
(e portanto não tem ep).
Mostre que o correspondente pl \eqref{lp:min-cost-pm} é inviável
e o pl \eqref{lp:dual:min-cost-pm} é
ilimitado.
Repita o exercício supondo que $G$ tem duas componentes conexas,
cada uma com número ímpar de nós.
-
★
Escreva explicitamente as desigualdades florais
do exemplo 9.8.
-
Desigualdades florais redundantes.
As desigualdades florais que são obviamente redundantes
podem ser eliminadas da seguinte maneira.
Escolha um nó qualquer $r$ como referência e
seja $\Fcal'$ o conjunto de todos os subconjuntos $S$ de $V\setm \conj{r}$
tais que $|S|$ é ímpar e $|S|\geq 3$.
Desenvolva essa ideia e corrija suas imperfeições.
-
★
Truque prático.
É interessante submeter o pl \eqref{lp:min-cost-pm}
a um software de programação linear.
Como $\Fcal$ é muito grande,
o seguinte truque prático pode ser útil:
use apenas uma pequena parte $\Fcal'$ de $\Fcal$
contendo os conjuntos $S$ mais
promissores
;
se isso não produzir
o vetor característico de um ep,
acrescente a $\Fcal'$ mais alguns elementos de $\Fcal$
que pareçam promissores e repita o processo.
-
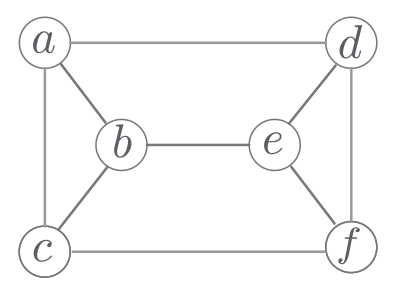
★
Encontre um ep
mínimo no grafo da figura.
Encontre também soluções ótimas dos pl's \eqref{lp:min-cost-pm}
e \eqref{lp:dual:min-cost-pm}.
(Dica:
Veja o exercício Truque prático.)
[CCPS 5.27]
-
Suponha que $(y,Y)$ é uma solução viável do pl \eqref{lp:dual:min-cost-pm}.
Para cada $S$ em $\Fcal$ e cada $v\in S$,
faça $y_v \larr y_v+Y_S$ ;
depois, para cada $S$, faça $Y_S\larr 0$.
Essa operação preserva a viabilidade de $(y,Y)$?
9.5 Algoritmo para ep mínimo em grafo arbitrário
Em 1965,
J. Edmonds
usou os pl's \eqref{lp:min-cost-pm}
e \eqref{lp:dual:min-cost-pm}
como ponto de partida
para obter um algoritmo que resolve o problema 9.A
do ep mínimo.
O algoritmo de Edmonds é conhecido como
algoritmo das flores para ep mínimo
(= blossom algorithm for minimum perfect matching).
O ponto de partida é o
algoritmo EmpPerfeito
da seção 7.6.
As flores produzidas por EmpPerfeito
correspondem, grosso modo,
aos conjuntos ímpares $S$ que têm $Y_S\neq 0$.
A discussão do algoritmo foge ao escopo destas notas.
Vou me limitar a exibir o código,
sem maiores explicações.
|
Blossom $(G,c)$
|
|
01
.
seja $y$ uma solução viável do pl \eqref{lp:dual:bipartite-min-cost-pm}
|
|
02
.
seja $M \subseteq \Eequ$ um emparelhamento em $G$
|
|
03
.
enquanto o emparelhamento $M$ não é perfeito faça
|
|
04
.ooo
$G' \larr G$, $c' \larr c$, $M' \larr M$
|
|
05
.ooo
seja $r$ um nó $M'$-exposto de $G'$
|
|
06
.ooo
$T' \larr (\conj{r},\emptyset)$
|
|
07
.ooo
repita
|
|
08
.oooooo
enquanto existe aresta preto-verde ou preto-preta em $\Eequ$
|
|
09
.ooooooooo
seja $vw$ uma aresta preto-verde ou preto-preta
|
|
10
.ooooooooo
se $vw$ é preto-verde
|
|
11
.oooooooooooo
então $T' \larr \text{}$ EstendeÁrvore $(G',M',T',vw)$
|
|
12
.oooooooooooo
senão ContraiFlor $(G',M',T',vw,c')$
|
|
13
.oooooo
se existe pseudonó branco $v$ tal que $y_v=0$
|
|
14
.ooooooooo
então expanda $v$ e atualize $M'$, $T'$, e $c'$
|
|
15
.oooooo
se não existe aresta preto-vermelha em $\Eequ$
|
|
16
.ooooooooo
então seja $A'$ o conjunto dos nós brancos de $T'$
|
|
17
.ooooooooo
então se $A'$ tem pseudonós
|
|
18
.oooooooooooo
então então $y\larr \text{}$ Ajuste $(G',c',M',T',y)$
|
|
19
.oooooooooooo
então senão devolva $A'$ e pare
|
|
20
.oooooo
seja $vw$ uma aresta preto-vermelha em $\Eequ$
|
|
21
.oooooo
$M' \larr \text{}$ AumentaEmp $(G',M',T',vw)$
|
|
22
.oooooo
estenda $M'$ a um ep $M$ em $G$
|
|
23
.
devolva $M$ e pare
|
Esse algoritmo pode ser implementado
de modo a consumir $\Oh(n^2m)$ unidades de tempo.
Exercícios 9.5
-
★
Use o algoritmo Blossom
para mostrar que um grafo $G$ tem um ep
se e somente se o pl \eqref{lp:min-cost-pm} é viável.
(Sugestão:
Se $G$ não tem ep,
mostre que o pl dual \eqref{lp:dual:min-cost-pm} é
ilimitado.)
[CCPS 5.28]