Capítulo 1
Caminhos dirigidos de custo mínimo
Este capítulo discute o problema dos caminhos dirigidos de custo mínimo
em grafos.
Algoritmos para esse problema são usados como ferramenta
na resolução de muitos problemas de otimização combinatória.
(Consulte o
índice remissivo
e os apêndices
para conferir as definições de termos técnicos.)
1.1 O problema
Uma rede
(= network)
consiste em um grafo dirigido $D$
e uma função
$c$ que atribui um número
real —
positivo, negativo, ou nulo —
a cada arco
de $D$.
(Seria mais realista supor que os custos são
números racionais,
uma vez que computadores digitais não conhecem números irracionais.)
Dizemos que $c$ é uma função-custo
ou vetor de custos.
Para cada arco $e$ de $D$, o número $c_e$ é o
custo de $e$.
[O custo de um arco não é necessariamente medido em unidades monetárias.
Ele pode ser medido em quilômetros, toneladas, horas, etc.
e pode até ser negativo.]
O custo
de um caminho dirigido
$\seq{v_0,e_1,v_1,e_2,\ldots,e_p,v_p}$ na rede $(D,c)$
é o número $c_{e_1}+c_{e_2}+\cdots+c_{e_p}$.
Cada arco contribui para essa soma
tantas vezes quantas aparece em $P$.
(Note que um caminho
pode ter arcos repetidos.
Essa generalidade é importante para o estudo
do problema do caminho de custo mínimo.)
Se o nome do caminho é $P$, seu custo é denotado por $c(P)$.
Se $P$ é quase-simples
e todos os seus arcos têm custo $1$
então $c(P)$ é o número de arcos de $P$.
Um caminho dirigido $P$ tem custo mínimo
se $c(P)\leq c(P')$ para todo caminho dirigido $P'$
que tenha a mesma origem
e o mesmo término
que $P$.
Problema 1.A (dos caminhos dirigidos mínimos)
Dado um nó $r$ de uma rede $(D,c)$,
encontrar, para cada nó $v$,
um caminho dirigido de $r$ a $v$
que tenha custo mínimo.
Dizemos que $r$ é o nó inicial da rede.
Podemos incorporar $r$ à definição da rede e dizer
rede $(D,c,r)$.
Além disso, podemos adotar a abreviatura caminho dirigido mínimo
para a expressão caminho dirigido de custo mínimo
.
Se os custos de todos os arcos forem
positivos
então todo caminho dirigido mínimo é
simples.
Se os custos forem arbitrários,
todo caminho dirigido mínimo
tem um subcaminho que é simples e mínimo.
(Veja exercício abaixo.)
Condições necessárias.
Para que uma instância
do problema 1.A tenha solução,
é necessário que todos os nós da rede estejam
ao alcance do nó inicial $r$.
É fácil verificar algoritmicamente se essa condição está satisfeita.
Uma segunda condição necessária para a existência de solução
é mais difícil de verificar:
é preciso que todos os
ciclos dirigidos
tenham custo não-negativo.
Adotaremos a abreviatura
ciclo dirigido negativo
para a expressão ciclo dirigido de custo negativo
.
Se uma instância do problema tem um ciclo dirigido negativo,
então,
para algum nó $v$ da rede,
não existe caminho dirigido mínimo de $r$ a $v$
pois existem caminhos dirigidos de $r$ a $v$
que têm custo menor que qualquer número dado.
Poderíamos dizer que o custo mínimo é $-\infty$ nesse caso.
Pergunta:
as duas condições necessárias que acabamos de apontar são suficientes?
Em outras palavras,
é verdade que toda instância do problema 1.A
que satisfaz as duas condições tem solução?
Mostraremos adiante que a resposta é afirmativa.
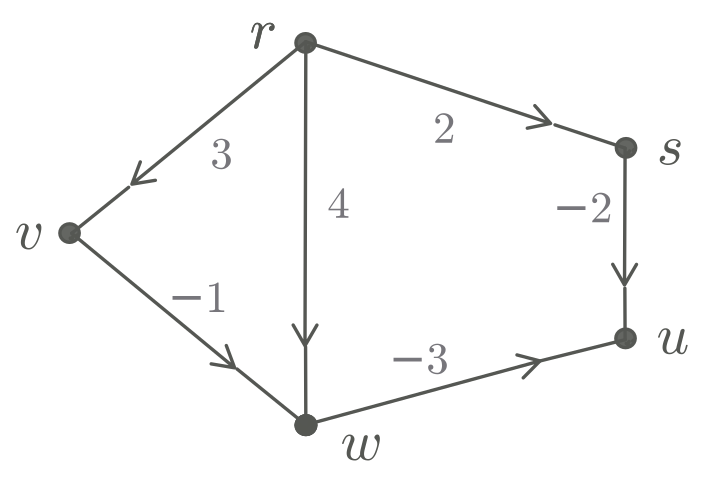
Exemplo 1.1:
Considere o grafo dirigido representado pela matriz de adjacências à esquerda
e o vetor de custos representado à direita.
Um caminho dirigido mínimo de $r$ a $u$
tem sequência de nós $\seq{r,v,w,u}$.
É um bom exercício encontrar os demais caminhos dirigidos mínimos.
\[
\begin{array}[t]{l@{\quad}ccccc}
& r & s & u & v & w \\[0.5ex]
r & - & 1 & - & 1 & 1 \\
s & - & - & 1 & - & - \\
u & - & - & - & - & - \\
v & - & - & - & - & 1 \\
w & - & - & 1 & - & -
\end{array}
\hspace{4ex}
\begin{array}[t]{rrrrrr}
rs& su& rw& wu& rv& vw \\[0.5ex]
2& -2& 4& -3& 3& -1
\end{array}
\]
Exemplo 1.2:
No grafo dirigido descrito abaixo não há caminho dirigido algum
de $r$ a $s$.
Essa instância do problema 1.A não tem solução,
qualquer que seja a função-custo.
\[
\begin{array}[t]{l@{\quad}ccc}
& r & s & t \\[0.0ex]
r & - & - & 1 \\
s & - & - & 1 \\
t & - & - & -
\end{array}
\]
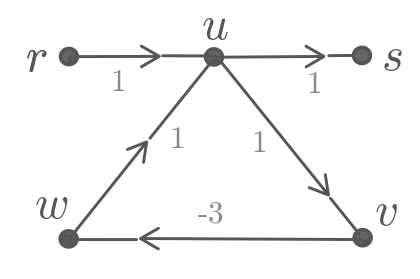
Exemplo 1.3:
Considere o grafo dirigido com custos representado abaixo.
Essa instância do problema 1.A
não tem solução porque não existe caminho dirigido
mínimo de $r$ a $s$.
(É um bom exercício exibir todos os caminhos dirigidos simples
de custo mínimo que têm origem $r$.)
\[
\begin{array}[t]{l@{\quad}ccccc}
& r & u & v & w & s \\[0.5ex]
r & - & 1 & - & - & - \\
u & - & - & 1 & - & 1 \\
v & - & - & - & 1 & - \\
w & - & 1 & - & - & - \\
s & - & - & - & - & -
\end{array}
\hspace{4ex}
\begin{array}[t]{rrrrr}
ru& uv& vw& wu& us \\[0.5ex]
1& 1& -3& 1& 1
\end{array}
\]
Exercícios 1.1
-
Esboce um algoritmo que decida
se todos os nós de um grafo dirigido estão ao alcance de
um dado nó $r$.
-
★
Caminhos mínimos simples.
Seja $P$ um caminho dirigido mínimo
numa rede $(D,c)$.
Mostre que algum subcaminho $P'$ de $P$
é dirigido,
é mínimo,
é simples,
e tem a mesma origem e o mesmo término de $P$.
-
★
Subcaminhos de caminhos mínimos.
Prove que qualquer subcaminho
de um caminho dirigido mínimo é mínimo.
Mostre que essa propriedade deixa de valer se nos restringirmos
a caminhos dirigidos simples.
[CCPS 2.19]
-
Árvores.
Calcule um caminho dirigido mínimo de $r$ a $v$ numa rede $(D,c)$
em que $D$ é um árvore radicada.
Calcule um caminho mínimo de $r$ a $v$ numa rede $(D,c)$
em que $D$ é uma árvore orientada.
-
★
Problema dos caminhos dirigidos simples mínimos.
Por que não restringir o problema 1.A
aos caminhos dirigidos quase-simples?
Melhor ainda: por que não restringir o problema 1.A
aos caminhos dirigidos simples?
Se fizermos isso, ciclos dirigidos negativos
deixarão de ser um empecilho para a existência de solução.
-
Dada uma rede $(D,c)$ e subconjuntos disjuntos $R$ e $S$ de $V(D)$
queremos encontrar um caminho dirigido mínimo
dentre os que vão de algum nó
de $R$ algum nó de $S$.
Mostre como esse problema
pode ser reduzido ao problema 1.A.
[CCPS 2.22]
-
No problema 1.A,
podemos supor que o grau de entrada de $r$ é $0$?
-
Suponha que uma rede $(D,c)$ tem ciclo dirigido de custo negativo.
Mostre que algum segmento
do ciclo é simples
e tem custo negativo.
1.2 Potencial viável
Como certificar a minimalidade de um caminho dirigido?
Dados nós $r$ e $v$,
como provar que nenhum caminho dirigido de $r$ a $v$
tem custo menor que um dado número, digamos $999$?
Um potencial numa rede $(D,c)$
é qualquer função que atribui um número real a cada nó da rede.
Podemos também dizer que um potencial é um
vetor indexado pelos nós da rede.
Usamos a seguinte terminologia para descrever o estado de um arco $vw$
em relação a um potencial $y$:
-
se $y_w - y_v \leq c_{vw}$
então $vw$ está relaxado,
-
se $y_w - y_v = c_{vw}$
então $vw$ está justo,
-
se $y_w - y_v > c_{vw}$
então $vw$ está tenso.
[Para justificar as palavras tenso e relaxado,
você pode imaginar que cada nó $v$ está no ponto de ordenada $y_v$ de uma reta
e cada arco $vw$ é um barbante
de comprimento $c_{vw}$.
Se a distância
$y_w-y_v$ é maior que o comprimento $c_{vw}$,
o arco $vw$ está esticado.
Senão, o arco está folgado.]
Um potencial $y$ é viável
(= feasible)
se deixa todos os arcos relaxados.
Em outras palavras, um potencial $y$ é viável se
$y_w - y_v \leq c_{vw}$
para cada arco $vw$.
Dizemos que esta é a
desigualdade triangular
para o arco $vw$.
A desigualdade pode se verbalizada assim:
o custo de um arco relaxado é pelo menos a diferença entre
o potencial de sua ponta final e
o potencial de sua ponta inicial.
Exemplo 1.4:
Se $c\geq 0$ e $y$ tem o mesmo valor em todos os nós
então $y$ é um potencial viável.
Exemplo 1.5:
Suponha que uma instância
do problema 1.A tem solução.
Para cada nó $v$,
seja $d_v$ o custo de um caminho dirigido mínimo de $r$ a $v$.
Então $d$ é um potencial viável.
Com efeito, se um arco $vw$ estivesse tenso,
teríamos $d_v + c_{vw} \lt d_w$
e então um caminho dirigido que vai de $r$ a $w$ passando por $vw$
teria custo menor que $d_w$,
o que é contraditório.
Em relação a um dado potencial,
se todos os arcos da rede estão relaxados
então todos os caminhos dirigidos também estão relaxados
num certo sentido.
O seguinte lema torna essa afirmação precisa:
Lema 1.1 (delimitação inferior)
Se $y$ é um potencial viável
e $P$ é um caminho dirigido com origem $r$ e término $s$
então $y_s - y_r \leq c(P)$.
Prova:
Seja $(v_0,e_1,v_1,\ldots,v_{k-1},e_k,v_k)$
o caminho $P$.
Adote as abreviaturas $c_i := c_{e_i}$
e $y_i := y_{v_i}$.
Então
\begin{align*}
c(P)
&= c_k + c_{k-1} + \cdots + c_2 + c_1 \\
&\geq y_k - y_{k-1} + y_{k-1} - y_{k-2} + \cdots + y_2 - y_1 + y_1 - y_0 \\
&= y_k - y_0.
\end{align*}
Portanto, $c(P) \geq y_{s} - y_{r}$,
como queríamos provar. ■
A prova do lema mostra, em particular, que
$c(P) = y_s - y_r$ se e somente se
todos os arcos de $P$ estão justos em relação a $y$.
O lema tem a seguinte consequência:
se $c(P) = \text{}$ $y_s - y_r$ então $P$ é mínimo.
Isso leva à seguinte condição de minimalidade para
o problema 1.A:
Corolário 1.2 (condição de minimalidade)
Numa rede $(D,c)$ com nó inicial $r$,
dada uma coleção $(P_w : w \in V(D))$ de caminhos dirigidos
em que cada $P_w$ tem origem $r$ e término $w$,
se existe um potencial viável $y$ tal que
$c(P_w) = \text{}$ $y_w-y_r$ para cada $w$
então cada $P_w$ é um caminho dirigido mínimo. ■
Exemplo 1.6:
Veja novamente o exemplo 1.1, repetido abaixo.
O potencial $y$ é viável.
Seja $P$ o caminho cuja sequência de nós é $(r,v,w,u)$.
Como $c(P) = -1 = y_u - y_r$, o caminho é mínimo.
\[
\begin{array}[t]{l@{\quad}ccccc}
& r & s & u & v & w \\[0.5ex]
r & - & 1 & - & 1 & 1 \\
s & - & - & 1 & - & - \\
u & - & - & - & - & - \\
v & - & - & - & - & 1 \\
w & - & - & 1 & - & -
\end{array}
\hspace{4ex}
\begin{array}[t]{rrrrrr}
rs& su& rw& wu& rv& vw \\[0.5ex]
2& -2& 4& -3& 3& -1
\end{array}
\hspace{4ex}
\begin{array}[t]{l@{\enspace}c}
& y \\[0.9ex]
r & 5 \\
s & 7 \\
u & 4 \\
v & 8 \\
w & 7
\end{array}
\]
Exercícios 1.2
-
Árvores.
Calcule um potencial viável numa rede $(D,c)$
em que $D$ é uma árvore radicada.
Calcule um potencial viável numa rede $(D,c)$
em que $D$ é uma árvore orientada.
-
Seja $y$ um potencial viável e $\alpha$ um número.
Mostre que $y - \alpha 1$ é um potencial viável.
(Aqui, $1$ é um vetor indexado pelos nós
e cada de seus elementos vale $1$.)
-
Prove o
corolário 1.2.
Prove também que a condição
existe um potencial viável $y$
tal que $c(P_w) = \text{}$ $y_w-y_r$ para cada $w$
equivale à condição
existe um potencial viável $y$ tal que
todos os arcos de cada $P_w$ estão justos
.
-
★
Potencial versus ciclo dirigido negativo.
Suponha que $y$ é um potencial viável numa rede.
Deduza do
lema 1.1
que a rede não tem ciclos dirigidos negativos.
-
Seja $(D,c,r)$ uma rede.
Para cada nó $w$, suponha dado
um caminho dirigido simples $P_w$ de $r$ a $w$.
Descreva um algoritmo que decida se a coleção $(P_w: w\in V(D))$ é
uma solução dessa instância do problema 1.A.
1.3 Algoritmo de Ford
O seguinte algoritmo tenta resolver o problema 1.A.
O algoritmo recebe uma rede $(D,c,r)$
e tenta encontrar uma coleção
de caminhos dirigidos mínimos:
para cada nó $w$ da rede,
um caminho dirigido $P_w$ com origem $r$ e término $w$.
O algoritmo só tem sucesso se
(1) todos os nós estão ao alcance de $r$ e
(2) a rede não tem
ciclos dirigidos negativos.
Se a condição (2) não estiver satisfeita,
a execução do algoritmo pode não parar
(portanto, a palavra algoritmo
é um abuso de linguagem).
O algoritmo foi proposto (1957) por
L. R. Ford.
Para certificar a minimalidade dos caminhos dirigidos,
o algoritmo produz um potencial viável $y$
tal que $c(P_w) = y_w-y_r$ para cada $w$.
|
Ford $(D, \ c, \ r)$
|
|
1
.
para cada $w$ em $V(D)$ faça $y_w \larr \infty$
|
|
2
.
$y_r \larr 0$
|
|
3
.
enquanto o potencial $y$ não é viável faça
|
|
4
.ooo
escolha $vw$ em $E(D)$ tal que $y_w - y_v > c_{vw}$
|
|
5
.ooo
$y_w\larr y_v+ c_{vw}$
|
|
6
.ooo
$\pred_w \larr v$
|
|
7
.
devolva $y$ e $\pred$
|
Na linha 4, $E(D)$ é o conjunto dos arcos de $D$
e o código adota a convenção $\infty+\lambda=\infty$
qualquer que seja $\lambda$.
Na linha 6,
o vetor $\pred$ representa caminhos com origem $r$ da seguinte maneira:
$\pred_w$
é o nó anterior a $w$ em um caminho dirigido de $r$ a $w$.
Dizemos que $p$ é uma função-predecessor
ou vetor de predecessores.
Portanto, a sequência
$\seq{w, \pred_{w}, \pred_{\pred_w}, \pred_{\pred_{\pred_w}}, \ldots, r}$
é o inverso de um caminho dirigido de $r$ até $w$.
O subgrafo de $D$
induzido pelo conjunto
de arcos da forma $(\pred_w,w)$
é uma árvore radicada
com raiz $r$.
A ideia do algoritmo é simples:
relaxar os arcos tensos, em qualquer ordem,
até que todos fiquem relaxados.
A operação de relaxação de um arco tenso (linha 5 do código)
consiste em baixar o potencial da ponta final do arco.
A relaxação de um arco tenso $vw$
pode tornar tenso outro arco $wz$ que estava relaxado.
Com isso, pode ser necessário relaxar um mesmo arco várias vezes.
Não está claro, portanto,
se a execução do algoritmo termina depois de um número finito de iterações.
Exemplo 1.7:
Aplique o algoritmo de Ford à rede que tem nós
$r \ s \ u \ v \ w$
e os arcos e custos indicados na tabela.
(Use o gabarito de posição dos nós para fazer uma figura.)
\[
\begin{array}[t]{rrrrrr}
rs& su& rw& wu& rv& vw \\
2& -2& 4& -3& 3& -1 \\
& & & & &
\end{array}
\]
\[
\begin{array}[t]{l@{\hspace{3ex}}l@{\hspace{5ex}}l}
&\hspace{3ex} r &\hspace{3ex} s \\[0.5ex]
v &\hspace{3ex} &\hspace{3ex} \\[0.5ex]
&\hspace{3ex} w &\hspace{3ex} u \\
\end{array}
\]
Veja os valores de $y$ (tabela esquerda)
e $\pred$ (tabela direita) no início de sucessivas iterações.
A última coluna da figura registra o arco que é relaxado no fim da iteração:
\[
\begin{array}{*{5}{r}}
r & s & u & v & w \\[0.6ex]
\hline
0 & \infty& \infty& \infty&\infty \\
0 & 2 & \infty& \infty&\infty \\
0 & 2 & \infty& 3 &\infty \\
0 & 2 & \infty& 3 & 4 \\
0 & 2 & 1 & 3 & 4 \\
0 & 2 & 0 & 3 & 4 \\
0 & 2 & 0 & 3 & 2 \\
0 & 2 & -1 & 3 & 2
\end{array}
\hspace{4ex}
\begin{array}{*{5}{c}}
r & s & u & v & w \\[1ex]
\hline
- & - & - & - & - \\
- & r & - & - & - \\
- & r & - & r & - \\
- & r & - & r & r \\
- & r & w & r & r \\
- & r & s & r & r \\
- & r & s & r & v \\
- & r & w & r & v
\end{array}
\quad
\begin{array}{*{1}{l}}
{} \\[1ex]
rs \\
rv \\
rw \\
wu \\
su \\
vw \\
wu \\
{}
\end{array}
\]
No fim da última iteração, $y$ é um potencial viável
e $\pred$ descreve caminhos dirigidos mínimos a partir de $r$.
Para analisar o algoritmo de Ford,
é preciso estabelecer os
invariantes
(não muito intuitivos)
do processo iterativo
descrito nas linhas 3 a 6.
O enunciado desses invariantes usa a seguinte notação:
$V^*$ é o conjunto dos nós $i$ para os quais $y_i \lt \infty$
e $D(\pred)$
é o subgrafo
de $D$ induzido pelo conjunto
de arcos da forma $(\pred_j,j)$.
Além disso, denotaremos por $\omega$
o número $\max_{vw \in E(D)} |c_{vw}|$.
[Não confunda $\omega$
com $w$
.]
Lema 1.3 (dos invariantes)
Se a rede $(D,c,r)$ não tem ciclo dirigido negativo
então, no início de cada iteração,
-
todo arco do grafo
$D(\pred)$ está justo ou tenso,
-
para cada arco $ij$ de $D$, se existe caminho dirigido
de $j$ a $i$ em $D(\pred)$
então $ij$ não está tenso,
-
para cada $i$ em $V^*$,
existe um caminho dirigido
de $r$ a $i$ em $D(\pred)$,
-
para cada $i$ em $V^*$, tem-se
$y_i \leq |V^*|\,\omega$.
Esboço de prova:
A relaxação de um arco tenso $vw$ na linha 5 do código
pode fazer com que outro arco $iw$, que estava justo ou tenso,
perca essa propriedade.
Como a linha 6 retira $iw$ de $D(\pred)$,
o invariante 1 é preservado.
Para provar o invariante 2,
suponha que $P$ é um caminho dirigido simples de $j$ a $i$
em $D(\pred)$.
Um raciocício análogo ao da prova
do lema 1.1,
combinado com o invariante 1,
mostra que $y_i - y_j \geq c(P)$.
Como $P\cdot (i,j)$ é um ciclo dirigido,
temos $c(P)+c_{ij}\geq 0$ e portanto o arco $ij$ não está tenso.
Para provar o invariante 3,
considere o arco $vw$ que será relaxado durante a iteração.
No início da iteração,
seja $P$ um caminho dirigido de $r$ a $v$ em $D(\pred)$.
Em virtude do invariante 2, $w$ não pertence a $P$.
Logo, no fim da iteração,
$P\cdot (v,w)$ será um caminho de $r$ a $w$ em $D(\pred)$. ■
Os invariantes 1 a 4
são a base da prova da correção do algoritmo de Ford.
A prova começa supondo que
(1) todos os nós da rede estão ao alcance de $r$ e
(2) a rede não tem
ciclos dirigidos negativos.
Quando
a execução do algoritmo termina,
todos os arcos estão relaxados, e portanto o potencial $y$ é viável.
Em particular, não existe arco $vw$ tal que
$y_v \lt \infty$ mas $y_w = \infty$.
Como todos os nós estão ao alcance de $r$,
temos $y_w \lt \infty$ para todo $w$,
e portanto $V^*=V(D)$.
O invariante 3 garante agora que, para cada $w$,
há um caminho dirigido
$P_w$ de $r$ a $w$ em $D(\pred)$.
O invariante 1 garante que
\[
c(P_w) \leq y_w-y_r
\]
(basta fazer um raciocínio análogo ao
da prova do lema 1.1).
Por outro lado, $c(P_w) \geq y_w-y_r$
pelo lema 1.1.
Assim, $c(P_w) = y_w-y_r$.
Segue daí e da condição de minimalidade
(corolário 1.2)
que o caminho $P_w$ é mínimo, como desejamos.
Para concluir a prova, precisamos garantir que
a execução do algoritmo termina depois de um número finito de iterações
se as hipóteses (1) e (2)
estiverem satisfeitas.
Será preciso supor também que o vetor $c$ não tem componentes irracionais.
Comecemos supondo que $c$ é inteiro.
Então, no início de cada iteração,
temos $y_i\leq n\omega$ para cada $i$ em $V^*$,
sendo $n$
o número de nós de $D$.
Por outro lado,
se $P_i$ é o caminho dirigido simples de $r$ a $i$ em $D(\pred)$
então $y_i - y_r \geq c(P_i)$ por um raciocínio
análogo ao da prova do lema 1.1.
Como $y_r=0$
e $P_i$ tem menos que $n$ arcos,
temos $y_i \geq c(P_i)\geq -n\omega$.
Em suma,
\[
-n\omega \leq y_i \leq n\omega
\]
para cada $i$ em $V^*$.
Ao longo da execução do algoritmo,
todas as componentes do vetor $y$ permanecem inteiras
e cada iteração subtrai pelo menos $1$ unidade
de alguma componente de $y$.
Como $-n\omega \leq y_w \leq n\omega$,
cada nó da rede pode fazer o papel de $w$ na linha 6
no máximo $2\omega n$ vezes.
Como $y$ tem $n$ componentes,
o número de iterações
não passa de $2 \omega n^2$.
Em particular, a execução do algoritmo
termina depois de um número finito de iterações se $c$ for inteiro.
Esse raciocínio pode ser estendido às instâncias em que os custos são
racionais.
Se $c$ é racional,
então existe $\zeta$ em $\Zplus$
tal que $\zeta c_e\in \Z$ para cada $e$.
Com isso, o número de iterações
não passa de $2 \omega n^2\zeta$.
Em particular, a execução do algoritmo termina
depois de um número finito de iterações se $c$ é racional.
Como a cota superior do número de iterações
depende dos custos dos arcos,
não podemos dizer que o algoritmo de Ford é polinomial,
mas apenas pseudopolinomial.
A próxima seção introduz uma variante do algoritmo
que organiza a ordem em que os arcos são relaxados
e assim torna o algoritmo
polinomial.
Exercícios 1.3
-
Complete a prova do lema 1.3.
Deduza dos invariantes 2 e 3 que $y_r=0$
no início de cada iteração.
-
Complete os detalhes da prova da correção do algoritmo de Ford.
-
Árvores.
Aplique o algoritmo de Ford a uma rede $(D,c,r)$
em que $D$ é uma árvore radicada.
Aplique o algoritmo de Ford a uma rede $(D,c,r)$
em que $D$ é uma árvore orientada.
-
Potencial finito.
Mostre que na linha 1 do algoritmo Ford
o $\infty$ pode ser substituído pelo número $n \omega$,
onde
$\omega := 1 + \max \left( |c_{e}| : e\in E(D) \right)$
e $n := |V(D)|$.
(Dica:
Qualquer caminho dirigido simples na rede tem
custo menor que $n\omega$.)
(Se essa substituição for feita,
será preciso adotar a convenção $n\omega+\lambda=n\omega$
qualquer que seja $\lambda$.)
1.4 Algoritmo de Ford–Bellman
Seja $S := \seq{e_1,e_2,e_3,\ldots, e_L}$ uma sequência de arcos
em que cada arco do grafo aparece pelo menos uma vez.
Imagine executar a parte central do algoritmo de Ford
examinando os arcos na ordem dada por $S$:
|
.
para $j = 1,\ldots, L$ faça
|
|
.ooo
se $e_j$ está tenso
|
|
.oooooo
então relaxe $e_j$
|
Dizemos então que $S$ é a sequência de varredura
usada pelo algoritmo.
Que condições uma sequência de varredura deve satisfazer
para que esse processo deixe todos os arcos do grafo relaxados?
Para discutir essa questão,
convém introduzir o conceito sde caminho imerso.
Um caminho dirigido está imerso na sequência de varredura $S$
se tiver origem $r$
e a sequência de seus arcos for uma
subsequência
de $S$.
(Se
$S = \seq{a, c,
d, a,
b, d,
e, c,
b, a,
d, b}$,
por exemplo,
então um caminho dirigido com origem $r$ e
sequência de arcos $\seq{c,a,d,e,b}$
está imerso em $S$.
Já um caminho dirigido com origem $r$ e sequência de arcos $\seq{c,e,d,a}$
não está imerso em $S$.)
Lema 1.4
Depois que uma sequência de varredura $S$ tiver sido processada,
tem-se $y_v \leq c(P)$ para cada nó $v$
e todo caminho dirigido $P$
de $r$ a $v$ que está imerso em $S$.
Prova:
Seja $\seq{v_0,e_1,v_1,e_2,v_2,\ldots,e_k,v_k}$ o caminho dirigido em discussão.
Imediatamente depois da primeira ocorrência de $e_1$ em $S$ temos
$y_{v_1} \leq \text{}$ $y_r + c_{e_1} = \text{}$ $c_{e_1}$
pois $y_r=0$
(veja exercício acima).
Desse momento em diante, a desigualdade $y_{v_1} \leq c_{e_1}$
permanece válida pois o valor de $y_{v_1}$ não aumenta.
Depois da primeira ocorrência de $e_2$ em $S$
subsequente à primeira ocorrência de $e_1$,
temos $y_{v_2} \leq \text{}$ $y_{v_1} + c_{e_2} \leq \text{}$
$c_{e_1} + c_{e_2}$.
E assim por diante.
Depois da primeira ocorrência de $e_k$ em $S$
subsequente às ocorrências de $e_1,e_2,\ldots,e_{k-1}$,
temos $y_{v_k} \leq \text{}$ $c_{e_1} + \cdots + c_{e_k} = \text{}$
$c(P)$. ■
Digamos que uma sequência de varredura $S$ é boa se
todo caminho dirigido simples com origem $r$ estiver imerso em $S$.
Como todo caminho dirigido mínimo é simples,
ao final do processamento de uma sequência boa teremos
$y_v \leq c(P)$ para todo caminho dirigido mínimo $P$ de $r$ a $v$.
Por outro lado, existe um caminho dirigido de $r$ a $v$ de custo $y_v$
(veja o lema 1.3).
Logo, o vetor $y$ representa os custos de todos os caminhos dirigidos mínimos
com origem $r$
(a menos, é claro, que a rede tenha um ciclo dirigido negativo).
Segue daí que a execução do algoritmo termina assim que
uma sequência de varredura boa for examinada.
Um tipo natural de sequência de varredura boa para uma rede com $n$ nós
é a que resulta da concatenação de sequências
$S_1, S_2, \ldots, S_{n-1}$ em que cada $S_i$ uma
permutação
do conjunto de arcos da rede.
Essa ideia leva ao algoritmo proposto por
R. E. Bellman (1958):
|
FordBellman $(D, \ c, \ r)$
|
|
1
.
para cada $w$ em $V(D)$ faça $y_w \larr \infty$
|
|
2
.
$y_r \larr 0$
|
|
3
.
repita $|V(D)|-1$ vezes
|
|
4
.ooo
para cada $vw$ em $E(D)$ faça
|
|
5
.oooooo
se $y_w - y_v > c_{vw}$
|
|
6
.ooooooooo
então $y_w \larr y_v+ c_{vw}$
|
|
7
.ooooooooo
então $\pred_w \larr v$
|
|
8
.
devolva $y$ e $\pred$
|
No fim da execução do algoritmo,
se o potencial $y$ é viável então $\pred$ define caminhos dirigidos mínimos
de $r$ a cada um dos demais nós
e $y_w$ é o custo do caminho dirigido que termina em $w$;
senão, a rede tem um ciclo dirigido negativo.
O algoritmo de Ford–Bellman
executa no máximo $nm$ iterações,
sendo $n := |V(D)|$ e $m := |E(D)|$.
O número de iterações
não depende do vetor de custos, como acontece no algoritmo de Ford.
A análise de correção que fizemos na seção anterior prova o seguinte:
Teorema 1.5 (Ford–Bellman)
Se a rede $(D,c,r)$ não tem
ciclo dirigido negativo
e todos os nós estão ao alcance de $r$,
o algoritmo de Ford–Bellman produz um
potencial viável $y$ e
um vetor de predecessores $\pred$ tais que, para cada nó $w$,
o caminho dirigido de $r$ a $w$ definido por $\pred$
tem custo $y_w - y_r$. ■
O teorema tem a seguinte consequência:
se a rede não tem ciclo dirigido negativo
e todos os nós estão ao alcance de $r$,
então existe um potencial viável $y$
tal que, para cada nó $w$,
a diferença $y_w - y_r$ é a
distância de $r$ a $w$,
ou seja, o custo de uma caminho de custo mínimo de $r$ a $w$.
Há quem diga que um tal $y$ é um potencial viável máximo.
Consumo de tempo.
Cada iteração do algoritmo de Ford–Bellman consome
$\Oh(1)$ unidades de tempo.
Portanto o algoritmo consome
\[
\Oh(nm)
\]
unidades de tempo.
Com isso, o algoritmo pode ser considerado fortemente polinomial.
Não se conhece uma versão do algoritmo de Ford que seja
assintoticamente mais rápida.
Para certos tipos de redes, entretanto,
há versões bem mais rápidas, como veremos nas próximas seções.
Exercícios 1.4
-
★
Corolário do teorema de Ford–Bellman.
Prove o seguinte corolário do teorema 1.5:
Uma instância $(D,c,r)$ do problema 1.A
tem solução se e somente se
(a) todos os nós de $D$ estão ao alcance de $r$ e
(b) a rede $(D,c)$ não tem ciclo dirigido negativo.
(Dica:
Enuncie e prove em separado a parte
se
e a parte somente se
.)
-
★
Potencial e distâncias.
Prove o seguinte corolário do teorema 1.5:
se a rede $(D,c,r)$ não tem ciclo dirigido negativo
e todos os nós estão ao alcance de $r$,
então existe um potencial viável $y$
tal que, para cada nó $w$, a diferença $y_w-y_r$
é a distância de $r$ a $w$.
-
Ciclos dirigidos negativos versus potencial.
Conforme o exercício Potencial versus ciclo dirigido negativo acima,
se uma rede tem um potencial viável então não tem ciclo dirigido negativo.
Use o
teorema 1.5
para provar a recíproca.
-
Considere uma instância do problema 1.A
em que todos os custos são
não-negativos
e todos os nós estão ao alcance de $r$.
Deduza do
teorema 1.5
que essa instância tem solução.
-
Considere uma instância do problema 1.A
em que o grafo é acíclico
e todos os nós estão ao alcance de $r$.
Deduza do
teorema 1.5
que essa instância tem solução.
-
Aplique o algoritmo FordBellman
ao grafo dirigido
com nós $r \ s \ t \ u \ v \ w$
e arcos $rs \ st \ tu \ uv \ vw\,$.
Todos os arcos têm custo $1$ e o nó inicial é $r$.
Examine o conjunto de arcos sempre na ordem
$\seq{vw,uv, tu, st, rs}$.
-
Prove a seguinte afirmação
(feita depois da prova do
lema 1.4):
se a rede não tem ciclo dirigido negativo
e a sequência de varredura $S$ é boa
então o potencial $y$ torna-se viável assim que o algoritmo
tiver processado $S$.
-
No algoritmo FordBellman,
não seria suficiente repetir
o bloco de linha 4--7 até que $y$ se
estabilize
?
Discuta essa ideia.
-
Potencial inteiro.
Suponha que a vetor $c$ de custos é inteiro.
Mostre que o potencial $y$ produzido pelo algoritmo de Ford–Bellman é inteiro.
-
Nem tudo ao alcance de $r$.
Como interpretar o resultado $(y, \pred)$ do algoritmo FordBellman
no caso em que nem todos os nós da rede estão ao alcance de $r$?
-
Árvores.
Escreva uma versão especializada do
algoritmo FordBellman
para redes $(D,c)$
em que $D$ é uma árvore radicada.
Escreva uma versão especializada de FordBellman
para redes $(D,c)$
em que $D$ é uma árvore orientada.
-
Aplique o algoritmo de Ford–Bellman à rede cujos nós são
$r \ a \ b \ f \ g \ h \ j \ k$
e cujos arcos e custos são dados pela tabela a seguir.
[CCPS 2.21]
\[
\begin{array}{*{17}{c}}
ra& rk& rb& ad& af& bk& bf& dh& fg& fj& gh& gj& jh& kd& kh& kg& kf\\
2& 7& 5& 8& 4& 3& 2& 5& 3& 7& 4& 3& 3& 2& 9& 6& 1
\end{array}
\]
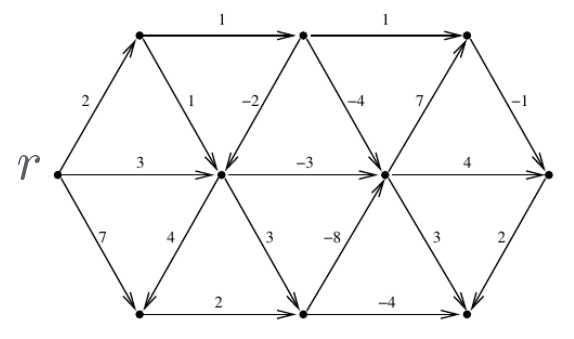
-
Mostre todos os caminhos dirigidos mínimos a partir do nó $r$.
Mostre um potencial viável que prove a minimalidade dos caminhos.
[Sch17 1.2]
1.5 Ciclos dirigidos negativos
O algoritmo de Ford–Bellman pode ser adaptado para procurar
ciclos dirigidos negativos
num grafo dirigido.
Se a execução do algoritmo terminar com um potencial $y$ não-viável,
o vetor de predecessores $\pred$ registra um ciclo dirigido negativo
a partir de qualquer arco que não esteja relaxado.
Exercícios 1.5
-
Acrescente código ao algoritmo FordBellman
para que ele devolva um ciclo dirigido negativo se tal existir.
-
Arbitragem cambial.
Seja $(D,c,r)$ uma rede com custos positivos.
Para cada nó $v$,
queremos encontrar um caminho dirigido de $r$ a $v$
que maximize o produto dos custos dos arcos do caminho dirigido.
Como resolver o problema?
(Aplicação: Cada nó é uma moeda, como dólar, euro, real, yen, etc.,
e o custo de um arco $vw$ é a taxa de câmbio
na conversão de $v$ em $w$.)
1.6 Algoritmo especial para redes acíclicas
Quando restrito a DAGs,
ou seja,
a grafos acíclicos,
o algoritmo de Ford–Bellman pode ser organizado de modo a
examinar cada arco uma só vez.
Comece com uma permutação topológica $v_1, v_2, \ldots, v_n$ dos nós
(conforme o lema F.2
no apêndice F,
um grafo é acíclico se e somente se tem uma permutação topológica).
Examine os arcos que saem de $v_1$,
depois os que saem de $v_2$, e assim por diante.
Como não tem ciclos dirigidos,
todo DAG satisfaz uma das condições necessárias
para que o problema 1.A
tenha solução.
Para que a outra condição —
todos os nós ao alcance do nó inicial $r$ —
esteja satisfeita é necessário (mas não suficiente) que tenhamos
$r = v_1$.
A versão do algoritmo de Ford–Bellman especializado em DAGs
recebe
uma permutação topológica $v_1,v_2,\ldots,v_n$ dos nós da rede
e procura resolver o problema dos caminhos dirigidos mínimos
a partir do nó inicial $v_1$:
|
FordBellmanDAG $(D, \ c, \ \seq{v_1,\ldots,v_n})$
|
|
1
.
para cada $w$ em $V(D)$ faça $y_{w} \larr \infty$
|
|
2
.
$y_{v_1} \larr 0$
|
|
3
.
para $i \larr 1$ até $n-1$ faça
|
|
4
.ooo
para cada $vw$ em $\cutout(v_i)$ faça
|
|
5
.oooooo
se $y_w - y_v > c_{vw}$
|
|
6
.ooooooooo
então $y_w \larr y_v + c_{vw}$
|
|
7
.ooooooooo
então $\pred_w \larr v$
|
|
8
.
devolva $y$ e $\pred$
|
Na linha 4,
$\cutout(v_i)$ denota o conjunto de todos os arcos que saem de $v_i$,
conforme seção F.5
do apêndice F.
A análise do algoritmo usa a ideia de
sequências de varredura boas da
seção 1.4.
Digamos que $S$ é a sequência
em que o algoritmo examina os arcos.
Então $S$ tem a seguinte propriedade:
se $i \lt j$ então todos os arcos em $\cutout(v_i)$
aparecem em $S$ antes de todos os arcos em $\cutout(v_j)$.
Portanto, todo caminho dirigido com origem $r$ está imerso em $S$.
De acordo com o
lema 1.4,
o potencial $y$ fica viável tão logo o algoritmo termina de percorrer $S$.
Consumo de tempo.
Como cada arco aparece apenas uma vez em $S$,
o algoritmo consome apenas $\Oh(m)$ unidades de tempo.
No fim da execução do algoritmo,
o vetor de predecessores $\pred$ define caminhos dirigidos mínimos
de $v_1$ a cada nó que esteja ao alcance de $v_1$.
Portanto, essa instância do problema 1.A
está resolvida se e somente se o algoritmo termina com $y_w \lt \infty$
para todo $w$.
Exercícios 1.6
-
Árvores radicadas.
Escreva uma versão especial do algoritmo FordBellmanDAG
para tratar de árvores radicadas.
-
Aplique o algoritmo FordBellmanDAG
à rede acíclica $(D,c,r)$
com nós $r \ s \ t \ u \ v$
e os arcos e custos definidos abaixo.
Adote a permutação topológica $\seq{r,s,t,u,v}$.
\[
\begin{array}{*{6}{c}}
rs& rt& su& st& tv& uv\\
2& 2& 4& 3& 1& -4
\end{array}
\]
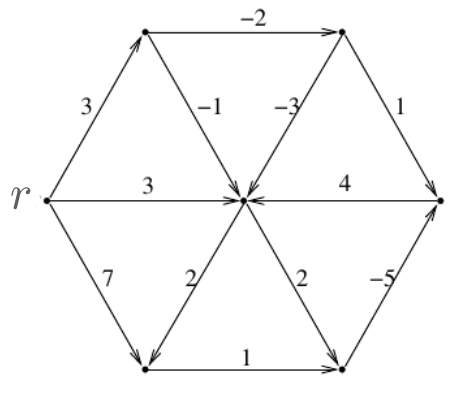
-
Mostre todos os caminhos dirigidos mínimos a partir do nó $r$ no grafo abaixo.
Mostre um potencial viável que prove a minimalidade dos caminhos.
[Sch17 1.2]
-
Suponha que $v_1,v_2,\ldots,v_n$ é uma permutação topológica dos nós
de uma rede.
Quero encontrar caminhos dirigidos mínimos
a partir de um nó $v_h$, com $h > 1$.
Modifique o algoritmo FordBellmanDAG
para resolver o problema.
-
Aplique o algoritmo FordBellmanDAG
à rede
cujos nós são
$r \ a \ b \ f \ g \ h \ j \ k$
e cujos arcos e custos são dados pela tabela a seguir.
[CCPS 2.21]
\[
\begin{array}{*{17}{c}}
ra& rk& rb& ad& af& bk& bf& dh& fg& fj& gh& gj& jh& kd& kh& kg& kf\\
2& 7& 5& 8& 4& 3& 2& 5& 3& 7& 4& 3& 3& 2& 9& 6& 1
\end{array}
\]
-
★
Segmento de soma mínima.
Dados números $e_1,\ldots,e_n$,
queremos encontrar $i$ e $j$,
$1 \leq i \leq j \leq n+1$,
tais que $e_i+\cdots+e_{j-1}$ seja mínimo.
Dê um algoritmo que resolva o problema em $\Oh(n)$ unidades de tempo.
[CCPS 2.34]
-
★
Escalonamento de tarefas.
Suponha dadas tarefas $T_1,\ldots,T_n$.
A execução de cada tarefa $T_i$ consome
tempo $c_i \geq 0$.
Para certos pares $(i,j)$,
a execução de $T_i$ deve preceder a execução de $T_j$
(ou seja, o processamento de $T_j$ só pode começar
depois que o processamento de $T_i$ tiver terminado).
Queremos planejar a execução das tarefas
de modo que as restrições de precedência sejam respeitadas
e cada tarefa seja concluída tão cedo quanto possível.
(Note que várias tarefas podem ser executadas ao mesmo tempo.)
Reduza esse problema ao cálculo de um
potencial viável máximo em um DAG.
[CCPS 2.35]
1.7 Algoritmo especial para custos não-negativos
Em redes sem arcos de custo negativo
(e portanto sem ciclos dirigidos negativos)
é possível acelerar o algoritmo de Ford–Bellman.
Para fazer isso, basta examinar os nós numa ordem especial,
à maneira do que fizemos com redes acíclicas.
Mas nesse caso a permutação dos nós não pode ser estabelecida de antemão,
devendo ser calculada à medida que o algoritmo é executado:
no começo de cada iteração,
o próximo nó da permutação é um nó $v$
que tem potencial mínimo dentre os nós que ainda não foram examinados.
Essa é a ideia do algoritmo que
E.W. Dijkstra
descobriu (1959).
O algoritmo de Dijkstra recebe uma rede $(D,c,r)$ com $c \geq 0$
e produz um vetor de predecessores $\pred$
e um potencial viável $y$.
Se todos os nós estiverem ao alcance de $r$,
o vetor $\pred$ define um caminho dirigido $P_v$ de $r$ a $v$
tal que $c(P_v) = y_v-y_r$.
|
Dijkstra $(D, \ c, \ r)$
|
|
01
.
para cada $w$ em $V(D)$ faça $y_w \larr \infty$
|
|
02
.
$y_r \larr 0$
|
|
03
.
$Q\larr V(D) \setm \conj{r}$
|
|
04
.
enquanto $Q \neq \emptyset$ faça
|
|
05
.ooo
escolha $v$ em $Q$ tal que $y_v$ é mínimo
|
|
06
.ooo
$Q \larr Q \setm \conj{v}$
|
|
07
.ooo
para cada $vw$ em $\cutout(v)$ faça
|
|
08
.oooooo
se $y_w - y_v > c_{vw}$
|
|
09
.ooooooooo
então $y_w \larr y_v + c_{vw}$
|
|
10
.ooooooooo
então $\pred_w \larr v$
|
|
11
.
devolva $\pred$ e $y$
|
O algoritmo mantém um conjunto $Q$ de nós que ainda não foram
completamente processados.
Para provar que o algoritmo está correto,
basta verificar que no início de cada iteração temos
(i1) $y_u \leq y_q$ para cada $u$ em $V(D)\setm Q$ e cada $q$ em $Q$ e
(i2) para cada $u$ em $V(D)\setm Q$,
todos os arcos em $\cutout(u)$ estão relaxados.
Assim, no fim da execução do algoritmo,
todos os arcos estarão relaxados
e portanto o potencial $y$ terá a propriedade desejada.
Consumo de tempo.
O algoritmo consome $\Oh(m) + \Oh(n^2)$ unidades de tempo,
sendo $n$ o número de nós e $m$ o número de arcos do grafo.
O termo $\Oh(m)$ reflete o fato de que cada arco
é processado no máximo uma só vez.
O termo $\Oh(n^2)$ é uma delimitação
do tempo total dispendido em todas as execuções de linha 05
(que escolhe $v$ em $Q$).
Como $m \lt n^2$,
o algoritmo consome $\Oh(n^2)$ unidades de tempo.
Exercícios 1.7
-
Mostre que o algoritmo de Dijkstra pode dar resultados errados
se a rede tiver algum ciclo dirigido negativo.
[CCPS 2.36]
-
★
Arcos negativos.
Mostre que o algoritmo de Dijkstra
pode produzir resultados errados
se o grafo tiver arcos de custo negativo,
mesmo que não tenho
ciclo negativo.
-
Prove os invariantes 1 e 2 do algoritmo Dijkstra.
-
Prove que $w \in Q$ sempre que o arco $vw$ está tenso na linha 08
do algoritmo Dijkstra.
-
Para $i=1,2,\ldots, v_{n-1}$,
seja $v_i$ o nó que o algoritmo Dijkstra escolha na linha 05
na $i$-ésima iteração.
Adote $v_0 := r$.
Agora considere a sequência $S = \seq{e_1,e_2,\ldots,e_m}$ de arcos
que o algoritmo examina nas sucessivas passagens pela linha 07:
primeiro todos os arcos que saem de $v_0$,
depois todos os arcos que saem de $v_1$,
e assim por diante.
Mostre que no fim da execução do algoritmo todos os caminhos dirigidos mínimos
que começam em $r$ estão imersos em $S$.
-
Aplique o algoritmo de Dijkstra à rede
cujos nós são
$r \ a \ b \ f \ g \ h \ j \ k$
e cujos arcos e custos são dados pela tabela a seguir.
[CCPS 2.21]
\[
\begin{array}{*{17}{c}}
ra& rk& rb& ad& af& bk& bf& dh& fg& fj& gh& gj& jh& kd& kh& kg& kf\\
2& 7& 5& 8& 4& 3& 2& 5& 3& 7& 4& 3& 3& 2& 9& 6& 1
\end{array}
\]
-
Translação de custos.
Suponha que a função-custo $c$ de uma rede tem valores negativos.
Eis uma ideia simples para eliminar os custos negativos.
Seja $\mu := \min (c_{e} : e \in E(D))$
e subtraia $\mu$ do custo de cada arco.
Agora todos os custos são não-negativos.
Execute o algoritmo de Dijkstra usando os novos custos.
Os caminhos dirigidos mínimos produzidos pelo algoritmo
têm custo mínimo em relação à função $c$ original?
[AMO 5.21]
-
Redes não-dirigidas.
Considere a variante do problema 1.A
que procura por caminhos não-dirigidos
mínimos em grafos
não-dirigidos
com custos não-negativos nas arestas.
Mostre como reduzir
esse problema ao
problema 1.A.
Qual a dificuldade de usar a mesma redução no caso de custos arbitrários?
[CCPS 2.37]
1.8 Custos unitários e busca em largura
A versão especializada do algoritmo de Dijkstra
para o caso em que $c=1$
é particularmente simples.
O conjunto $Q$ do algoritmo Dijkstra
pode ser tratado como uma fila
e inicializado com $\conj{r}$.
|
BuscaEmLargura $(D, \ r)$
|
|
01
.
para cada $w$ em $V(D)$ faça $y_w \larr \infty$
|
|
02
.
$y_r \larr 0$
|
|
03
.
$Q\larr \text{}$ InicializaFila$\,(r)$
|
|
04
.
enquanto FilaNãoVazia$\,(Q)$ faça
|
|
05
.ooo
$v \larr \text{}$ TiraDaFila$\,(Q)$
|
|
06
.ooo
para cada $vw$ em $\cutout(v)$ faça
|
|
07
.oooooo
se $y_w - y_v > c_{vw}$
|
|
08
.ooooooooo
então $y_w \larr y_v + c_{vw}$
|
|
09
.ooooooooo
então $\pred_w \larr v$
|
|
10
.ooooooooo
então PõeNaFila$\,(Q, w)$
|
|
11
.
devolva $\pred$ e $y$
|
Esta versão do algoritmo de Dijkstra é conhecida como
busca em largura.
Ela consome $\Oh(m)$ unidades de tempo.
Exercícios 1.8
-
Árvores.
Escreva uma versão especial de BuscaEmLargura
para árvores radicadas.
Escreva uma versão especial de BuscaEmLargura
para árvores orientadas.
-
★
Caminhos versus cortes.
Sejam $r$ e $s$ dois nós de um grafo dirigido.
Dizemos que um corte dirigido separa $s$ de $r$
se existe um conjunto $S$ de nós tal que $s\in S$,
$r\notin S$ e
$\cutin(S)=\emptyset$.
Mostre que um corte dirigido separa $s$ de $r$
se e somente se
não existe caminho dirigido de $r$ a $s$.
(Dica:
Enuncie e prove em separado a parte
se
e a parte somente se
.)
1.9 Programação linear
Retornamos agora ao problema 1.A
sem quaisquer restrições:
procuramos caminhos dirigidos de custo mínimo
em grafos arbitrários (não necessariamente acíclicos)
com custos arbitrários (não necessariamente não-negativos).
Esta seção estuda o problema do ponto de vista da programação linear.
A aplicação de uma ferramenta contínua, como programação linear,
a um problema discreto e combinatório
pode parecer surpreendente.
Mas problemas combinatórios têm aspectos geométricos
de que podemos tirar bom proveito por meio da programação linear.
Essa intrusão do mundo contínuo no mundo discreto é bem-vinda e
muito frutífera.
Nosso ponto de partida é a delimitação inferior
estabelecida no lema 1.1 e o
teorema de Ford–Bellman (teorema 1.5).
Esses resultados têm a seguinte consequência:
Teorema 1.6 (min-max)
Dados dois nós $r$ e $s$ de uma rede $(D,c)$,
se $s$ está ao alcance de $r$
e a rede não tem ciclo dirigido negativo
então
\[
\max_y\,(y_s - y_r) = \min_P\,c(P)\text{,}
\]
sendo $\max_y$ tomado sobre todos os potenciais viáveis $y$ e
$\min^{}_P$ tomado sobre todos os caminhos dirigidos $P$ de $r$ a $s$. ■
O problema de encontrar um potencial viável $y$ que maximize $y_s-y_r$
é facilmente formulado como um programa linear:
encontrar um vetor
$y$ indexado por $V(D)$ que
\begin{equation}\label{lp:max-feasible-potential}
\begin{split}
\text{maximize} \enspace y_s-y_r & \\
\text{sujeito a} \enspace y_w- y_v &\leq c_{vw}
\enspace \text{para $vw$ em $E(D)$.}
\end{split}
\end{equation}
Convém reescrever este pl
em termos da
matriz de incidências $A$ do grafo.
Como a coluna $vw$ de $A$ tem um $-1$ na linha $v$, um $+1$ na linha $w$,
e $0$ nas demais linhas,
o pl \eqref{lp:max-feasible-potential} equivale a
\begin{equation*}
\begin{split}
\text{maximize} \quad y\,b & \\
\text{sujeito a} \quad yA &\leq c\,\text{,}
\end{split}
\end{equation*}
onde $b$ é o vetor
definido por
$b_r = -1$,
$b_s = +1$,
e $b_v = 0$ para todo $v$ diferente de $r$ e de $s$.
Exemplo 1.8:
Seja $y$ o vetor e $A$ a matriz representados abaixo.
Suponha que o vetor $y$ e as linhas da matriz $A$ são indexados
por $r,v,w,s$ de cima para baixo.
Então o vetor representado abaixo de $A$
é $yA$.
\[
\begin{array}[t]{r@{\qquad}rrrrr}
-2 \enspace & -1 & -1 & 0 & 0 & 0 \\
3 \enspace & +1 & 0 & -1 & -1 & 0 \\
-4 \enspace & 0 & +1 & +1 & 0 & -1 \\
5 \enspace & 0 & 0 & 0 & +1 & +1 \\[1.5ex]
\enspace & 5 & -2 & -7 & 2 & 9
\end{array}
\]
Programa dual.
O dual do pl \eqref{lp:max-feasible-potential} pede
um vetor $x$ indexado por $E(D)$
que
\begin{equation*}% \label{lp:matrix:shortest-paths}
\begin{split}
\text{minimize} \quad cx & \\
\text{sujeito a} \quad A x &= b \\
x &\geq 0\,\text{.}
\end{split}
\end{equation*}
Para verificar que este é de fato o dual,
tome qualquer solução viável
$y$ do primal,
qualquer solução viável
$x$ do dual,
e observe que a prova
\[
yb = y(A x) = (yA)x \leq cx
\]
do teorema fraco da dualidade
usa
todas as restrições dos dois pl's.
Exemplo 1.9:
Seja $A$ a matriz e $x$ o vetor representados abaixo
com $x$ na horizontal abaixo de $A$.
Suponha que o vetor $x$ e as colunas de $A$ são indexados
por $a,b,c,d,e$ da esquerda para a direita.
Então o vetor representado à direita de $A$ é $A x$.
\[
\begin{array}[t]{rrrrr@{\qquad}r}
-1 & -1 & 0 & 0 & 0 & \enspace -1 \\
+1 & 0 & -1 & -1 & 0 & \enspace 0 \\
0 & +1 & +1 & 0 & -1 & \enspace 0 \\
0 & 0 & 0 & +1 & +1 & \enspace +1 \\[1.5ex]
1 & 0 & 1 & 0 & 1 &
\end{array}
\]
Na matriz de incidências $A$ de $D$, a linha que corresponde ao nó $v$
tem um $-1$ na coluna de cada arco que entra em $v$,
um $+1$ na coluna de cada arco que sai de $v$,
e $0$ nas demais colunas.
Portanto, o pl pode ser reescrito assim:
\begin{equation}\label{lp:shortest-paths}
\begin{split}
\text{minimize} \enspace \textstyle\sum_{e \in E} c_e x_e & \\
\text{sujeito a} \enspace
\xin(r) - \xout (r) &= -1 \\
\xin(v) - \xout (v) &= 0 \enspace \text{para $v$ em $V\setm\conj{r,s}$} \\
\xin(s) - \xout (s) &= +1 \\
x_{e} &\geq 0 \enspace \text{para $e$ em $E$,}
\end{split}
\end{equation}
sendo $E:=E(D)$ e $V:=V(D)$.
A expressão $\xin(v)$
é uma abreviatura de $x(\cutin(v))$
e denota a soma dos valores de $x$ nos arcos que entram em $v$.
Analogamente,
$\xout(v)$ é a soma dos valores de $x$ nos arcos que saem em $v$.
Em notação formal,
$\xin(v) := \text{}$ $\sum_{u\, :\, uv \in E} x_{uv}$
e
$\xout(v) := \text{}$ $\sum_{w\, :\, vw \in E} x_{vw}$.
O pl \eqref{lp:shortest-paths}
está relacionado com os caminhos dirigidos mínimos de $r$ a $s$.
De fato, para todo caminho dirigido simples $P$ de $r$ a $s$,
o vetor característico do conjunto de arcos de $P$ é uma solução viável do pl
(e portanto $c(P) \geq cx^*$ para qualquer
solução ótima
$x^*$ do pl).
Folgas complementares.
A relação fraca de dualidade entre os
pl's \eqref{lp:max-feasible-potential}
e \eqref{lp:shortest-paths}
consiste na sequência de igualdedes e desigualdades
$yb = \text{}$ $y(A x) = \text{}$ $(yA)x \leq cx$,
válida para qualquer solução viável $y$ do pl primal
e qualquer solução viável $x$ do dual.
Portanto, $yb=cx$ se e somente se $(yA)x = cx$,
ou seja, se e somente se
\[\textstyle
\sum_{vw\in E} ((y_w-y_v) - c_{vw}) x_{vw} = 0\text{.}
\]
Como $(y_w-y_v) \leq c_{vw}$ e $x\geq 0$,
essa igualdade vale se e somente se,
para cada arco $vw$,
\[
x_{vw} = 0 \quad \text{ou} \quad y_w-y_v = c_{vw}\text{.}
\]
Essas são as condições de folgas complementares
do par dual de pl's.
Essas condições correspondem à seguinte afirmação:
todos os arcos de qualquer caminho dirigido mínimo de $r$ a $s$ estão justos
em relação ao potencial $y$.
Soluções ótimas dos pl's.
Suponha que o pl \eqref{lp:max-feasible-potential} é viável
e o pl \eqref{lp:shortest-paths} é viável.
Nessas condições,
o teorema forte da dualidade
garante que o pl \eqref{lp:max-feasible-potential}
tem uma solução ótima $y^*$,
que o pl \eqref{lp:shortest-paths} tem uma solução ótima $x^*$,
e que
\[
y^* b = c x^*\text{.}
\]
Mesmo que $x^*$ não seja o vetor característico de um caminho dirigido,
o número $cx^*$ é igual ao custo de um caminho mínimo de $r$ a $s$.
Para verificar essa afirmação,
basta lembrar que $cx^* = y^*b$
e observar que
o teorema de Ford–Bellman
(teorema 1.5)
garante que $y^*b$ é igual ao custo de um caminho mínimo.
Exercícios 1.9
-
Prove o teorema min-max
(teorema 1.6)
a partir do teorema de Ford–Bellman
(teorema 1.5)
e do lema 1.1.
-
É verdade que toda solução ótima $x$ do pl \eqref{lp:shortest-paths}
tem a propriedade $0 \leq x \leq 1$?
-
Prove que todo caminho dirigido simples de $r$ a $s$
descreve uma solução viável do pl \eqref{lp:shortest-paths}.
Prove que qualquer caminho dirigido mínimo de $r$ a $s$
descreve uma solução ótima do pl \eqref{lp:shortest-paths}.
-
É verdade que toda solução viável binária do pl \eqref{lp:shortest-paths}
descreve um caminho dirigido de $r$ a $s$?
É verdade que toda solução ótima do pl \eqref{lp:shortest-paths}
descreve um caminho dirigido de $r$ a $s$?
-
★
Escalonamento de tarefas (mais uma vez).
Refaça o exercício Escalonamento de tarefas
depois de representar o problema por um programa linear.
[CCPS 2.35]
1.10 Poliedros e seus vértices
Para entender a relação entre os pl's \eqref{lp:max-feasible-potential}
e \eqref{lp:shortest-paths}
e o problema 1.A,
é preciso estudar os poliedros dos pl's.
Quai são as propriedades
geométricas desses poliedros?
Em que condições esses poliedros são vazios?
Como são os vértices
desses poliedros?
O poliedro dos potenciais viáveis
Seja $Y(D,c)$
o poliedro do pl \eqref{lp:max-feasible-potential}, isto é,
o conjunto de todos os vetores $y$ que satisfazem as restrições $yA\leq c$.
Se o grafo $D$ tem um ciclo dirigido negativo então $Y(D,c)$ é vazio
conforme o lema 1.1.
A recíproca é verdadeira, embora menos óbvia:
se a rede não tem um ciclo dirigido negativo então $Y(D,c)$ não é vazio.
Agora considere a existência de vértices
em $Y(D,c)$.
Para qualquer $y$ em $Y(D,c)$,
os vetores $y+1$ e $y-1$
também estão em $Y(D,c)$,
pois $y_w+1-y_v+1 = \text{}$ $y_w-y_v$.
(Aqui, $1$
representa o vetor constante
cujas componentes são todas iguais a $1$.)
Portanto, $Y(D,c)$ não tem vértices.
A continuação dessa argumentação acaba por mostrar que $Y(D,c)$ não é limitado
(ou seja, não cabe em um cubo).
Exemplo 1.10:
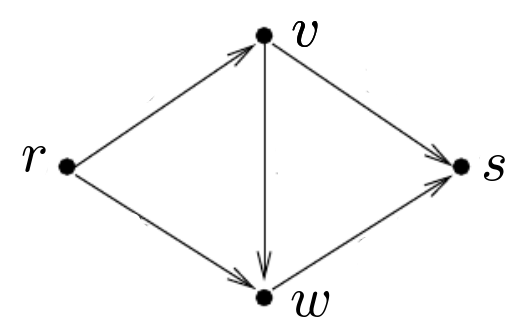
Seja $D$ a rede com nós $r \ v \ w \ s$
definida pela matriz de incidências $A$ à esquerda
e considere o vetor de custos $c$ à direita.
\[
\begin{array}[t]{l@{\quad}ccccc}
& rv & rw & vw & vs & ws \\[0.5ex]
r & -1 & -1 & & & \\
v & +1 & & -1 & -1 & \\
w & & +1 & +1 & & -1 \\
s & & & & +1 & +1
\end{array}
\hspace{0ex}
\hspace{6ex}
\begin{array}[t]{rrrrr}
rv& rw& vw& vs& ws \\[0.5ex]
5& 7& 1& 8& 6
\end{array}
\]
Veja as restrições que definem o poliedro $Y(D,c)$
escritas explicitamente abaixo.
Veja também um vetor de $Y(D,c)$ mais à direita.
\[
\begin{split}
y_v - y_r &\leq 5\\
y_w - y_r &\leq 7\\
y_w - y_v &\leq 1\\
y_s - y_v &\leq 8\\
y_s - y_w &\leq 6
\end{split}
\hspace{6ex}
\begin{array}[c]{r@{\enspace}r}
r & 0 \\
v & 5 \\
w & 6 \\
s & 12
\end{array}
\]
Observe que $1A=0$.
(Toda matriz de incidências tem essa propriedade.
Na linguagem da álgebra linear, diríamos que
o conjunto das linhas de $A$ é linearmente dependente.)
Logo, para qualquer $y$ em $Y(D,c)$, temos $(y\pm 1)A = yA \leq c$.
Isso mostra que $Y(D,c)$ não tem vértices.
Ademais, o poliedro $Y(D,c)$ não é limitado,
uma vez que $y+\alpha 1$ está em $Y(D,c)$
qualquer que seja $y$ em $Y(D,c)$ e
qualquer que seja $\alpha$ real.
O poliedro dos caminhos
Seja $X(D,r,s)$
o poliedro do pl \eqref{lp:shortest-paths}, isto é,
o conjunto de todos os vetores $x$ que satisfazem as restrições
$A x = b$ e $x\geq 0$.
Em que condições o poliedro é vazio?
Em que condições é limitado?
Como são seus vértices?
É evidente que
o vetor característico de qualquer caminho dirigido
de $r$ a $s$ pertence ao poliedro $X(D,r,s)$.
Reciprocamente,
para qualquer vetor $x$ do poliedro,
existe um caminho dirigido de $r$ a $s$ cujos arcos
pertencem ao suporte
de $x$.
Assim, $X(D,r,s)$ é vazio se e somente se
não existe caminho dirigido de $r$ a $s$.
(Veja um dos exercícios abaixo.)
Quanto à limitação,
o poliedro $X(D,r,s)$
é limitado se e somente se $D$ é um DAG.
Mas isso não impede que uma instância do pl \eqref{lp:shortest-paths}
tenha solução ótima mesmo que $D$ tenha ciclos dirigidos.
Agora considere as propriedades dos vértices do poliedro.
É fácil constatar que
o vetor característico de qualquer caminho dirigido simples de $r$ a $s$
é vértice do poliedro.
Como mostraremos a seguir, esses são os únicos vértices do poliedro.
Seja $x$ um vetor de $X(D,r,s)$
e $C$ um ciclo (dirigido ou não)
de $D$ cujos arcos estão no suporte
de $x$.
Seja $\epsilon:=\min_{e \in E(C)} x_e$
e $\d$ o vetor definido assim:
$\d_e$ vale $\epsilon$ se $e$ é um
arco direto
de $C$,
vale $-\epsilon$ se $e$ é um
arco inverso
de $C$,
e vale $0$ em todos os demais casos.
Então $\d$ não é nulo e tanto $x+\d$ quanto $x-\d$ estão no poliedro.
A existência de um tal $\d$ mostra que $x$ não é vértice do poliedro.
Concluímos assim que, para todo vértice $x$ do poliedro,
todo ciclo
de $D$ tem pelo menos um arco $e$ tal que $x_e=0$.
Em outras palavras, se $S$ é o suporte de um vértice do poliedro
então o grafo $(V(D),S)$ é uma
floresta orientada.
Como nenhum nó, exceto $r$ e $s$, é folha da floresta,
todo vértice do poliedro é o vetor característico
de um caminho dirigido simples de $r$ a $s$.
Exemplo 1.11:
Considere novamente a rede $D$ do exemplo 1.10.
Ela tem nós $r \ v \ w \ s$
e é definida pela matriz de incidências abaixo.
\[
\begin{array}[t]{l@{\quad}ccccc}
& rv & rw & vw & vs & ws \\[0.5ex]
r & -1 & -1 & & & \\
v & +1 & & -1 & -1 & \\
w & & +1 & +1 & & -1 \\
s & & & & +1 & +1
\end{array}
\]
Veja as restrições lineares que definem o poliedro $X(D,r,s)$:
\[
\begin{array}{*{5}{r}@{\enspace}c@{\enspace}rr}
-x_{rv}& {}-x_{rw}& & & & = & -1 & \\
x_{rv}& & {}-x_{vw}& {}-x_{vs}& & = & 0 & \\
& x_{rw}& {}+x_{vw}& & {}-x_{ws}& = & 0 & \\
& & & x_{vs}& {}+x_{ws}& = & +1 & \\
x_{rv}& & & & & \geq & 0 & \\
& x_{rw}& & & & \geq & 0 & \\
& & x_{vw}& & & \geq & 0 & \\
& & & x_{vs}& & \geq & 0 & \\
& & & & x_{ws}& \geq & 0 &\text{.}
\end{array}
\]
Os vetores $x'$, $x''$,
$x'''$ e $x'''''$
abaixo pertencem ao poliedro $X(D,r,s)$.
\[
\begin{array}[t]{l@{\quad\enspace}rrrrr}
& rv & rw & vw & vs & ws \\[0.5ex]
x' & 1 & 0 & 0.5 & 0.5 & 0.5 \\
x'' & 0.6 & 0.4 & 0.3 & 0.3 & 0.7 \\
x''' & 1 & 0 & 1 & 0 & 1 \\
x'''' & 1 & 0 & 0 & 1 & 0
\end{array}
\]
O vetor $x'$, por exemplo, não é vértice pois
tanto $x'+\d'$ quanto $x'-\d'$ estão em $X(D,r,s)$
quando $\d'$ é o vetor dado abaixo.
Esse vetor é definido pelo ciclo $(v,w,s,v)$
e todos os arcos deste ciclo estão no suporte de $x'$.
\[
\begin{array}[t]{l@{\quad\enspace}rrrrr}
& rv & rw & vw & vs & ws \\[0.3ex]
\d' & 0 & 0 & 0.1 & -0.1 & 0.1
\end{array}
\]
O vetor $x''$ não é vértice de $X(D,r,s)$ em virtude do ciclo $(r,w,s,v,r)$.
Os vetores $x'''$ e $x''''$ são vértices do poliedro $X(D,r,s)$.
Ambos representam caminhos dirigidos simples de $r$ a $s$.
Exemplo 1.12:
Seja $X(D,r,s)$ o poliedro definido pelas restrições $A x = b$ e
$x\geq 0$,
onde $A$ é a matriz de adjacências abaixo.
(Use o gabarito de posição dos nós para fazer uma figura do grafo.)
Os vetores $x$ e $x'$ representados à direita pertencem a $X(D,r,s)$.
O vetor $x$ sugere que $X(D,r,s)$ não é limitado
(note o ciclo dirigido $(u,v,w,u)$).
\[
\begin{array}[t]{l@{\quad}cccccc}
& ru & uv & us & vw & wu \\[0.5ex]
r & -1 & & & & \\
u & +1 & -1 & -1 & & +1 \\
v & & +1 & & -1 & \\
w & & & & +1 & -1 \\
s & & & +1 & &
\end{array}
\hspace{6ex}
\begin{array}[t]{*{5}{c@{\hspace{2ex}}}}
& \\
r & & u & & s \\[3.5ex]
& w & & v &
\end{array}
\]
\[
\begin{array}[t]{l@{\quad}rrrrr}
& ru& uv& vw& wu& us \\[0.5ex]
x & 1& 99& 99& 99& 1 \\[0.2ex]
x'& 1& 0& 0& 0& 1
\end{array}
% \hspace{23ex} % hack
\]
Se $\d$ é o vetor característico do ciclo $(u,v,w,u)$,
então tanto $x+\d$ quanto $x-\d$ pertencem a $X(D,r,s)$.
Logo, $x$ não é vértice de $X(D,r,s)$.
Já $x'$ é vértice de $X(D,r,s)$.
Note que $x'$ é o vetor característico de
um caminho dirigido simples de $r$ a $s$.
Suponha que o pl \eqref{lp:shortest-paths}
tem solução ótima
para um determinado vetor de custos $c$.
De acordo com o corolário C.3
no apêndice C,
alguma solução ótima do pl é vértice do poliedro $X(D,r,s)$.
Portanto, alguma solução ótima do pl
é (o vetor característico de) um caminho dirigido simples
de $r$ a $s$.
Podemos supor então
que qualquer algoritmo de programação linear —
como o Simplex, por exemplo —
resolve o problema 1.A.
Mas é claro que
um algoritmo especializado,
como o de Ford–Bellman, é mais eficiente.
Exercícios 1.10
-
Mostre que $Y(D,c) = \emptyset$
se e somente se a rede tem um ciclo dirigido negativo.
-
★
Mostre que $X(D,r,s) = \emptyset$
se e somente se não existe caminho dirigido de $r$ a $s$.
-
★
Mostre que $X(D,r,s)$ é limitado se e somente se
$D$ não tem ciclos dirigidos.
-
★
Seja $P$ um caminho dirigido de $r$ a $s$.
Seja $x$ o vetor característico de $E(P)$.
Mostre que $x$ é vértice do poliedro $X(D,r,s)$.
-
★
Vértices versus ciclos.
Prove que $x$ é vértice de $X(D,r,s)$
se e somente se $D$ não tem ciclo (dirigido ou não)
cujos arcos estão no suporte de $x$.
-
★
Vértices são caminhos dirigidos.
Mostre que todo vértice do poliedro $X(D,r,s)$
é o vetor característico de um caminho dirigido simples de $r$ a $s$.
Mais exercícios
-
Suponha dada uma rede $(D,c,r)$
e um nó $w$ que incide em exatamente dois arcos
(ou seja, apenas dois arcos têm $w$ como ponta inicial ou ponta final).
Mostre como reduzir
o problema dos caminhos dirigidos mínimos nessa rede a uma rede menor.
[CCPS 2.23]
-
★
Árvores.
Seja $(T,c)$ uma rede em que $T$ é uma
árvore orientada
e $c$ uma função-custo.
Escreva um algoritmo que receba $T$,
$c$, e um nó $r$,
e calcule, para cada nó $v$,
um caminho (não necessariamente dirigido!)
de custo mínimo de $r$ a $v$ em $T$.
-
Suponha que $(D,c,r)$ é uma rede em que todos os arcos têm o mesmo custo.
Qual o algoritmo assintoticamente mais rápido para
resolver o problema dos caminhos dirigidos mínimos nessa rede?
-
Suponha que $r$, $s$ e $t$ são três nós de uma
rede com custos não-negativos.
Queremos encontrar um caminho dirigido mínimo dentre os que começam em $r$,
passam por $s$, e terminam em $t$.
Uma solução desse problema é necessariamente um caminho dirigido simples?
Descreva informalmente um algoritmo para resolver o problema.
Prove que o seu algoritmo resolve o problema.
[AMO 4.45]
-
Capacidade mínima.
Digamos que a capacidade
de um caminho dirigido é o mínimo dos custos de seus arcos.
Problema: Determine um caminho dirigido de capacidade mínima
dentre os que vão de $r$ a $s$.
-
Custos diretos e custos inversos.
Cada arco $e$ de uma rede tem dois custos,
$c'_{e}$ e $c''_{e}$, ambos reais.
O custo de um caminho $P$, não necessariamente dirigido,
é $\sum c'_{e}+\sum c''_{e}$,
onde a primeira soma se estende a todos os arcos diretos de $P$
e a segunda a todos os arcos inversos de $P$.
Problema: Determinar um caminho de custo mínimo
dentre os que vão de um nó $r$ a um nó $s$.
Enuncie uma condição de otimalidade apropriada.
-
Caminhos dirigidos de comprimento ímpar.
Numa rede com custos não-negativos e dois nós $r$ e $s$,
considere o problema de encontrar um caminho dirigido mínimo de $r$ a $s$
dentre os que têm um número ímpar de arcos.
Note que um caminho dirigido
pode não ser simples.
Mostre como reduzir
esse problema ao
problema 1.A.
(Sugestão:
Troque cada nó diferente de $r$ e $s$ por dois novos nós.)
Repita o exercício depois de trocar
ímpar
por par
.
[CCPS 2.38]
-
Análise de sensibilidade.
Seja $(D,c,r)$ uma rede sem ciclos dirigidos negativos.
Para cada nó $v$,
digamos que $d_v$ é a distância
de $r$ a $v$,
ou seja, o custo de um caminho dirigido mínimo de $r$
a $v$.
De quanto podemos diminuir o custo de um certo arco $ij$
sem que os valores da função $d$ se alterem?