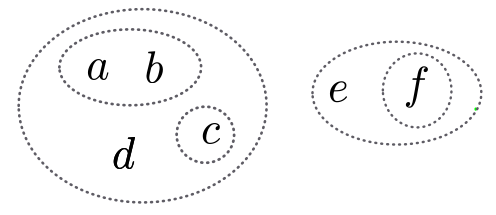Otimização Combinatória | Dicionário | Índice remissivo

Apêndice A
Conjuntos, vetores e matrizes

Este apêndice estabelece algumas convenções de notação e terminologia a respeito de vetores e matrizes. Também introduz o conceito de coleção laminar de conjuntos.

A.1 Vetores

Um vetor indexado por um conjunto finito $M$ é o mesmo que uma função que leva $M$ em algum conjunto de números. (Não é uma boa ideia supor que o conjunto de índices é necessariamente $\conj{1,2,\ldots,n}$ ou $\conj{0,1,2,\ldots,n-1}$.)  Um vetor $x$ indexado por $M$ pode ser indicado por \[ (x_i : i\in M)\text{.} \]

Note que não há vetores-linha nem vetores-coluna. Um vetor é apenas um vetor, sem adjetivos.

Um vetor real indexado por $M$ é uma função que leva $M$ em $\R$. Da mesma forma, um vetor racional indexado por $M$ é uma função que leva $M$ em $\Q$. O conjunto de tais funções é tradicionalmente denotado por \[ \Q^M\,\text{.} \]

Um vetor é não-negativo se todos as suas componentes são não-negativas. Um vetor é inteiro se todos as suas componentes pertencem a $\Z$. Um vetor é binário, ou booleano, se todas as suas componentes pertencem a $\conj{0,1}$.

Se $x$ é um vetor indexado por um conjunto $M$ e $K$ é um subconjunto de $M$, denotamos por $x_K$ ou por $x[K]$ a restrição de $x$ a $K$. É claro que $x[M] = x$.

A.2 Matrizes

Considere o produto cartesiano $M\times N$ de dois conjuntos finitos $M$ e $N$. Uma matriz indexada por $M\times N$ é um função que leva $M\times N$ em algum conjunto de números. Uma matriz $A$ indexada por $M\times N$ pode ser indicada por $(A_{i,j} : i\in M, j\in N)$ ou por $(A[i,j] : i\in M, j\in N)$.

Uma matriz é real se todos as suas componentes pertencem a $\R$. Uma matriz é racional se todos as suas componentes pertencem a $\Q$ e inteira se todos as suas componentes pertencem a $\Z$. Uma matriz é binária, ou booleana, se todas as suas componentes pertencem a $\conj{0,1}$.

Se $A$ é uma matriz indexada por $M\times N$ e $i$ é um elemento de $M$, a linha $i$ de $A$ é o vetor $(A_{i,j} : j\in N)$. Esse vetor pode ser denotado por $A_{i,N}$ ou por $A[i,N]$.

Se $j$ é um elemento de $N$, a coluna $j$ de $A$ é o vetor $(A_{i,j} : i\in M)$. Esse vetor pode ser denotado por $A_{M,j}$ ou por $A[M,j]$.

Podemos usar o símbolo $*$ para indicar o conjunto de todas as linhas e o conjunto de todas as colunas. Assim, $A[i,*] := A[i,N]$ e $A[*,j] := A[M,j]$.

Se $A$ é uma matriz indexada por $M\times N$ e $K$ e $L$ são subconjuntos de $M$ e $N$ respectivamente então $A[K,L]$ denota a restrição de $A$ ao conjunto de índices $K\times L$.

A transposta de uma matriz $A$ indexada por $M\times N$ é a matriz $B$ indexada por $N\times M$ e definida pela seguinte propriedade: $B[j,i] = A[i,j]$ para cada $j$ em $N$ e cada $i$ em $M$. A transposta de $A$ é denotada por $\tr{A}$.

Para qualquer conjunto finito $N$, a matriz identidade indexada por $N\times N$ é a matriz binária $\Id$ definida pelas seguintes propriedades: para cada $(i,j)$ em $N\times N$, se $i = j$ então $\Id{}[i,j] = 1$ e se $i\neq j$ então $\Id{}[i,j] = 0$.

Para qualquer conjunto finito $N$, uma permutação dos elementos de $N$ é uma sequência em que cada elemento do conjunto aparece uma e uma só vez. Uma permutação de $N$ é o mesmo que uma bijeção, digamos $p$, de $N$ em $N$. A matriz de permutação correspondente a $p$ é a matriz binária $P$ indexada por $N\times N$ e definida pelas seguintes propriedades: para cada $(j,i)$ em $N\times N$, se $j = p(i)$ então $P[j,i] = 1$ e se $j\neq p(i)$ então $P[j,i] = 0$.

Essa definição pode ser generalizada como segue. Para quaisquer conjuntos finitos $M$ e $N$ de mesma cardinalidade e qualquer bijeção $q$ de $M$ em $N$, a matriz de bijeção correspondente a $q$ é a matriz binária $Q$ indexada por $N\times M$ e definida pelas seguintes propriedades: para cada $(j,i)$ em $N\times M$, se $j = q(i)$ então $Q[j,i] = 1$ e se $j\neq q(i)$ então $Q[j,i] = 0$.

A.3 Produtos

Para quaisquer vetores $c$ e $x$ indexados por um mesmo conjunto $M$, denotamos por  $c\,x$  a soma de todos os números da forma $c_ix_i$ com $i$ em $M$: \[\textstyle cx := \sum\nolimits_{i\in M} c_ix_i\,\text{.} \] Esta soma também pode ser escrita assim: $\sum \left( c_ix_i : i\in M \right)$. Se $M = \conj{1,2,3,4}$, por exemplo, então $cx = c_1x_1+c_2x_2+c_3x_3+c_4x_4$.  [Muita gente escreve $\tr{c}x$ no lugar do meu $cx$. Mas a transposição de um vetor não faz sentido, uma vez que não existem vetores-linha nem vetores-coluna.]

Para qualquer matriz $A$ indexada por $M\times N$ e qualquer vetor $x$ indexado por $N$, denotamos por $Ax$ a soma de vetores \[\textstyle \sum_{j\in N} A[\all,j] x[j]\,\text{.} \]

Para qualquer vetor $y$ indexado por $M$, denotamos por  $yA$  a soma de vetores \[\textstyle \sum\nolimits_{i\in M} y[i] A[i,\all]\,\text{.} \]

[Muita gente escreve $\tr{A}y$ no lugar do meu $yA$. Eu prefiro a notação mais simples.]  O produto de um vetor por uma matriz não é comutativo: $yA$ não é o mesmo que $Ay$ (em geral, um deles nem faz sentido). 

Para qualquer vetor $c$ indexado por um conjunto $M$ e qualquer subconjunto $K$ de $M$, denotamos por  $c(K)$  a soma de todos os $c_k$ com $k$ em $K$: \[\textstyle c(K) := \sum\nolimits_{k\in K} c_k\text{.} \]

Essa soma também pode ser escrita assim: $\sum \left( c_k : k \in K \right)$. Se $x$ é o vetor característico do subconjunto $K$ de $M$ então $c(K) = cx$.

A.4 Álgebra linear

Ao longo desta seção, suporemos $M$ e $N$ são dois conjuntos finitos e $A$ é uma matriz real indexada por $M\times N$.  [Poderíamos nos restringir às matrizes racionais, uma vez que computadores digitais desconhecem números irracionais.] 

Um conjunto de linhas de $A$ é essencialmente o mesmo que uma submatriz da forma $A[K,\all]$, com $K \subseteq M$. Um conjunto de colunas de $A$ é essencialmente o mesmo que uma submatriz da forma $A[\all,L]$, com $L \subseteq N$.

Uma combinação linear das colunas de $A$ é qualquer vetor da forma $Ax$, sendo $x$ um vetor real indexado por $N$. Uma combinação linear das linhas de $A$ é qualquer vetor da forma $yA$, sendo $y$ um vetor real indexado por $M$.

O conjunto das colunas de $A$ é linearmente dependente se existe um vetor real $x$ indexado por $N$ tal que $x \neq 0$ mas $Ax = 0$. Em outras palavras, o conjunto das colunas de $A$ é linearmente dependente se alguma coluna de $A$ pode ser escrita como combinação linear das demais.  O conjunto das colunas de $A$ é linearmente independente se não for linearmente dependente, ou seja, se a matriz $A$ não tem colunas redundantes.

Definições análogas valem para as linhas de $A$. O conjunto das linhas de $A$ é linearmente dependente se existe um vetor real $y$ indexado por $M$ tal que $y \neq 0$ mas $yA = 0$. O conjunto das linhas de $A$ é linearmente independente se não for linearmente dependente.

Usamos as expressões l.d. e l.i. como abreviaturas de linearmente dependente e linearmente independente respectivamente.

Adotamos a seguinte terminologia simplificada: um subconjunto $K$ de $M$ é l.i. se o conjunto das colunas da matriz $A[K,\all]$ é l.i.. Um conjunto l.i. $K$ é maximal se não for subconjunto próprio de outro conjunto l.i..

O posto de linhas (= row rank) de $A$ é o tamanho de qualquer subconjunto l.i. maximal de $M$.

Definição análoga vale para subconjuntos de $N$ e para o conceito de posto de colunas (= column rank) de $A$.

O posto (= rank) de $A$ é, indiferentemente, o posto de linhas ou o posto de colunas de $A$.

A.5 Coleções laminares de conjuntos

Seja $\Lcal$ uma coleção de subconjuntos de um conjunto finito $V$.  [A palavra coleção é sinônima de conjunto. Usaremos coleção para designar um conjunto de conjuntos.]  Diremos que $V$ é nosso universo.  A coleção $\Lcal$ é laminar se, para cada par $(X,Y)$ de elementos de $\Lcal$, temos \begin{equation}\label{eq:laminar-property} X\cap Y=\emptyset \quad\text{ou}\quad X\subseteq Y \quad\text{ou}\quad X\supseteq Y\,\text{.} \end{equation}

Toda coleção laminar de subconjuntos de $V$ tem no máximo $2|V|$ elementos e portanto é muito menor que a coleção de todos os subconjuntos de $V$.

Exemplo A.2: Suponha que nosso universo $V$ é $\conj{a,b,c,d,e,f,g}$. A coleção $\conj{\conj{a,b,c,d}, \conj{a,b}, \conj{c}, \conj{e,f},\conj{f}}$ é laminar. Ela pode ser representada, de maneira muito compacta, pela expressão $((a\ b)\ (c)\ d)\ (e\ (f))$, em que cada elemento do universo aparece no máximo uma vez.

Exemplo A.3: Suponha que $X$ e $Y$ são dois subconjuntos do universo $V$. A coleção $\conj{X, Y, X\cup Y}$ é laminar. A coleção $\conj{X, \compl{X}}$ também é laminar. Em particular, a coleção $\conj{V, \emptyset}$ é laminar.

Coleções laminares têm caráter recursivo: se $\Lcal$ é uma coleção laminar de subconjuntos de $V$ e $X$ é um elemento de $\Lcal$ então a coleção $\conj{L\in \Lcal : L\subseteq X}$ também é laminar. Assim, toda coleção laminar $\Lcal$ tem a estrutura de uma árvore radicada: o conjunto de nós da árvore é $\Lcal \cup {\conj{V}}$ e cada arco da árvore tem a forma $(X,Z)$, sendo $X$ um elemento de $\Lcal \cup {\conj{V}}$ e $Z$ um elemento maximal de $\conj{L\in \Lcal : L\subset X}$. A raiz da árvore é $V$.

É claro que uma coleção é laminar se e somente se $X\cap Y=\emptyset$ ou $X\cap \compl{Y}=\emptyset$ ou $\compl{X}\cap Y=\emptyset$ para cada par $(X,Y)$ de elementos da coleção.  A laminaridade de uma coleção tem uma relação interessante com a operação de complementação: