Muitos problemas de otimização combinatória são formuladas sobre grafos. Este apêndice faz uma rápida revisão dos conceitos e da terminologia da teoria dos grafos dirigidos.
Um grafo dirigido
(= directed graph)
é um par $(V,E)$ de conjuntos
em que $V$ é um conjunto finito não vazio e
$E$ um conjunto de pares ordenados de elementos de $V$.
(Alguns livros dizem digrafo
(= digraph)
no lugar de grafo dirigido.)
Os elementos de $V$ são chamados nós
e os elementos de $E$ são chamados arcos
(= arcs).
[As letras $V$
e $E$
são as iniciais de
vertex
e edge,
respectivamente.
(Quem sabe deveríamos escrever $N$
e $A$
em lugar de $V$
e $E$
.)
A palavra vértice será aplicada apenas a vértices
de poliedros.]
Se $E$ é um conjunto de todos os pares ordenados de elementos de $V$,
dizemos que o grafo $(V,E)$ é completo.
Podemos dar um nome — como $D$, por exemplo — a um grafo dirigido. Nesse caso, o conjunto de nós do grafo é denotado por $V(D)$ e o conjunto de arcos por $E(D)$.
Um arco $(v,w)$ pode ser denotado simplesmente por $vw$.
O nó $v$ é a
ponta inicial
(= tail)
e o nó $w$ é a ponta final
(= head)
do arco.
Dizemos que um tal arco
sai de $v$ e
entra
em $w$.
A ponta inicial de um arco também pode ser chamada
ponta negativa
e a ponta final pode ser chamada
ponta positiva.
[Outros livros adotam a convenção de circuitos elétricos
e dizem que a ponta inicial é positiva
e a ponta final é negativa
.]
Se $vw$ é um arco, dizemos que $w$ é
vizinho direto
de $v$
e $v$ é
vizinho inverso
de $w$.
As pontas inicial e final de cada arco são distintas,
e portanto grafos dirigidos não têm laços
(= loops).
Além disso,
grafos dirigidos não têm arcos paralelos
,
pois dois arcos diferentes não podem ter a mesma ponta inicial
e a mesma ponta final.
Dois arcos $vw$ e $v'w'$
são antiparalelos
se $v' = w$ e $w' = v$.
O grau de entrada (= indegree) de um nó $v$ é o número de arcos que têm ponta final $v$. O grau de saída (= outdegree) de $v$ é o número de arcos que têm ponta inicial $v$. Uma fonte (= source) é qualquer nó que tenha grau de entrada nulo. Um sorvedouro (= sink) é qualquer nó que tenha grau de saída nulo.
O número de nós de um grafo dirigido é denotado por $n$ e o número de arcos por $m$. Portanto, se $D$ é o grafo em discussão então $n := |V(D)|$ e $m := |E(D)|$. É claro que $m\leq n(n-1) \lt n^2$.
Um subgrafo de um grafo dirigido $D$ é qualquer grafo dirigido $D'$ tal que $V(D')\subseteq V(D)$ e $E(D')\subseteq E(D)$. Se $V(D')=V(D)$, dizemos que $D'$ é um subgrafo gerador (= spanning). Dado um subconjunto $V'$ de $V(D)$, se $E'$ é o conjunto de todos os arcos de $D$ que têm ambas as pontas em $V'$, dizemos que o subgrafo $(V',E')$ é induzido por $V'$. Esse grafo é denotado por $G[V']$. Dado um subconjunto $E'$ de $E(D)$, se $V'$ é o conjunto de todos os nós de $D$ que são ponta de arco de $E'$, dizemos que subgrafo $(V',E')$ é induzido por $E'$.
Para qualquer nó $v$ de $D$, denotamos por $D-v$ o subgrafo induzido por $V(D)\setm\conj{v}$. Para qualquer arco $e$, denotamos por $D-e$ o subgrafo que tem conjunto de nós $V(D)$ e conjunto de arcos $E(D)\setm\conj{e}$.
Para qualquer par $(v,w)$ de nós, denotamos por $D+vw$ o grafo dirigido que tem conjunto de nós $V(D)$ e conjunto de arcos $E(D)\cup\conj{vw}$.
Um grafo dirigido $D$ é bipartido se existe uma bipartição, digamos $\conj{P,Q}$, de $V(D)$ tal que todo arco tem ponta inicial em $P$ e ponta final em $Q$.
O grafo não-dirigido subjacente a (= underlying) um grafo dirigido $D$ é o grafo não-dirigido $G$ tal que $V(G) = V(D)$ e $vw \in E(G)$ se e somente se $vw \in E(D)$ ou $wv \in E(D)$. Em termos informais, $G$ é o grafo não-dirigido que se obtém quando ignoramos as orientações de todos os arcos de $D$.
Uma orientação (= orientation) de um grafo não-dirigido $G$ é qualquer grafo dirigido $D$ que satisfaz as seguintes condições: $V(D) = V(G)$ e, para cada aresta $vw$ de $G$, um e apenas um dos pares ordenado $vw$ e $wv$ é arco de $D$. Em termos informais, $D$ é o grafo dirigido que se obtém quando adotamos uma das duas possíveis orientações de cada aresta de $G$. É claro que orientações de grafos não-dirigidos não têm arcos antiparalelos.
Um caminho (= path)
num grafo dirigido é qualquer sequência alternante
$\seq{v_0,e_1, v_1,e_2,\ldots, e_p,v_p}$
de nós e arcos tal que, para cada $k$,
o arco $e_k$ tem ponta inicial $v_{k-1}$ e ponta final $v_k$
ou tem ponta final $v_{k-1}$ e ponta inicial $v_k$.
(Note que os nós de um caminho não são necessariamente
distintos dois a dois.
A mesma observação vale para os arcos.)
Se $e_k = v_{k-1}v_k$, o arco $e_k$ é direto;
se $e_k = v_kv_{k-1}$, o arco $e_k$ é inverso.
Podemos dizer que os arcos diretos apontam da esquerda para a direita
,
enquanto arcos inversos apontam da direita para a esquerda
.
O nó $v_0$ é a origem do caminho e o nó $v_p$ é o término. Dizemos que o caminho vai de $v_0$ a $v_p$. O comprimento do caminho é $p$, ou seja, o número de termos do caminho que são arcos. O conjunto de nós de um caminho $P$ é denotado por $V(P)$ e o conjunto de arcos por $E(P)$.
Um caminho $P'$ é subcaminho de um caminho $P$ se pode ser obtido pela remoção de termos de $P$. (Por exemplo, $(u,a,v, b,w, e,z)$ é um subcaminho de $(u,a,v,b, w,c,x, d,v,b, w,e,z)$.) Um caminho $P'$ é segmento de um caminho $P$ se pode ser obtido pela remoção de termos do início e/ou do fim de $P$. (Por exemplo, $(x,d,v,b, w,e,z)$ é um segmento de $(u,a,v,b, w,c,x, d,v,b, w,e,z)$.)
Um caminho $\seq{v_0,e_1, v_1,e_2,\ldots, e_p,v_p}$ é quase-simples (= edge-simple) se não tem arcos repetidos, isto é, se os arcos $e_1, e_2,\ldots,e_p$ são diferentes entre si. (Nada impede, entretanto, que o caminho tenha nós repetidos. E nada impede que o caminho tenha um arco antiparalelo a outro.) Se $P$ é um caminho quase-simples então o comprimento de $P$ é igual a $|E(P)|$.
Um caminho é simples se não tem nós repetidos. (É claro que todo caminho simples é, em particular, quase-simples.) Se $P$ é um caminho com origem $r$ e término $s$ então algum subcaminho de $P$ é um caminho simples de $r$ a $s$.
Dados caminhos $\seq{v_0,e_1,\ldots,v_p}$ e $\seq{w_0, f_1,\ldots, w_q}$, se o término do primeiro é igual à origem do segundo, então os dois caminhos podem ser concatenados. O resultado da concatenação é o caminho $\seq{v_0,e_1,\ldots,v_p, f_1,\ldots, w_q}$. A concatenação de dois caminhos $P$ e $Q$ é denotada por $P \cdot Q$.
Caminhos dirigidos. Um caminho é dirigido (= dipath) se todos os seus arcos são diretos. Dizemos que um nó $v$ de um grafo dirigido está ao alcance de um nó $r$ se existe um caminho dirigido de $r$ a $v$.
Conexão. Um grafo dirigido é conexo se o grafo não-dirigido subjacente for conexo. Em outras palavras, um grafo dirigido é conexo se, para cada par $(r,s)$ de seus nós, existe um caminho (não necessariamente dirigido) de $r$ a $s$ (e portanto também um caminho de $s$ a $r$).
Uma componente conexa de um grafo dirigido $D$ é um subgrafo conexo maximal de $D$.
Um grafo dirigido é fortemente conexo se, para cada par $(r,s)$ de seus nós, existe um caminho dirigido de $r$ a $s$ e um caminho dirigido de $s$ a $r$.
Ciclos. Um ciclo (= cycle) é um caminho quase-simples $\seq{v_0,e_1,v_1,\ldots, e_p,v_p}$ em que $v_p=v_0$ e $p \geq 2$. Um ciclo é dirigido se todos os seus arcos são diretos.
Lema F.1 (folclore) Se todos os nós de um grafo dirigido têm grau de entrada e grau de saída não nulos então o grafo tem um ciclo dirigido. ■
Um ciclo é simples se não tem nós repetidos exceto o último (que coincide com o primeiro). Todo ciclo tem um segmento que é um ciclo simples.
Um grafo dirigido é acíclico se não tem ciclos dirigidos. Grafos dirigidos acíclicos também são conhecidos pela abreviatura DAG de directed acyclic graph. Todos os caminhos dirigidos de um DAG são simples.
Lema F.2 (folclore) Um grafo dirigido é acíclico se e somente se tem uma permutação topológica. ■
Uma permutação $v_1,v_2,\ldots,v_n$ do conjunto dos nós de um grafo dirigido é
topológica
se $i \lt j$ para cada arco $v_iv_j$, isto é,
se todos os arcos apontam da esquerda para a direita
na permutação.
Lema F.3 (folclore) Em qualquer DAG, todo arco pertence a um caminho dirigido que começa em uma fonte e termina em um sorvedouro. ■
Uma floresta orientada (= oriented forest) é um grafo dirigido sem ciclos (em particular, sem ciclos dirigidos). Portanto, toda floresta orientada é um DAG. O grafo não-dirigido subjacente a uma floresta orientada é uma floresta. Reciprocamente, toda floresta orientada é uma orientação de uma floresta.
Uma árvore orientada (= oriented tree) é uma floresta orientada conexa. Em outras palavras, uma árvore orientada é uma orientação de uma árvore.
Para quaisquer dois nós $r$ e $s$ de uma árvore orientada, existe um e um só caminho simples de $r$ a $s$. Para todo arco $e$ de uma árvore orientada $T$, o grafo dirigido $T-e$ é uma floresta orientada com exatamente duas componentes conexas.
Florestas e árvores radicadas. Uma floresta radicada (= rooted forest) é uma floresta orientada cada um de cujos nós tem grau de entrada $0$ ou $1$. Os nós com grau de entrada $0$ são as raízes da floresta radicada. Toda floresta radicada tem pelo menos uma raiz. Todo nó $v$ de uma floresta radicada é término de um único caminho dirigido simples que começa numa raiz.
Uma folha de uma floresta radicada é um nó que tem grau de entrada $1$ e grau de saída $0$.
Uma árvore radicada (= rooted tree) é uma floresta radicada que tem uma só raiz. Árvores radicadas também são conhecidas como arborescências e como árvores divergentes.
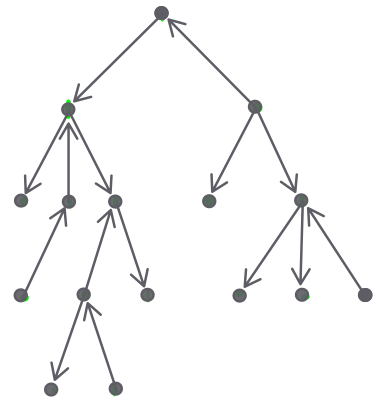
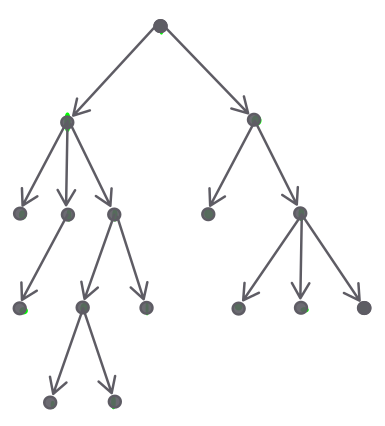
Exemplo F.1: A primeira figura representa uma árvore orientada. A segunda representa uma árvore radicada.
Exemplo F.2: Seja $T$ uma árvore radicada. Para cada arco $e$ de $T$, seja $X_e$ o conjunto de nós da componente conexa de $T-e$ que contém a ponta final de $e$. (Em outras palavras, $X_e$ é o conjunto de todos os nós de $T$ que estão ao alcance da ponta final de $e$.) A coleção $\conj{X_e : e\in E(T)}$ é laminar.
Dado um grafo dirigido $(V,E)$ e um subconjunto $R$ de $V$, denotamos por $\compl{R}$ o conjunto $V\setm R$. Dizemos que um arco $vw$ entra em $R$ se $v\in \compl{R}$ e $w\in R$. Dizemos que $vw$ sai de $R$ se $v\in R$ e $w\in \compl{R}$. O conjunto de todos os arcos que saem de $R$ é denotado por \[ \cutout(R)\,\text{.} \]
(O $\text{}^{-}$
na notação decorre de
nossa convenção
sobre qual das pontas de um arco é positiva e qual é negativa.)
Analogamente, $\cutin(R)$
é o conjunto de todos os arcos que entram
em $R$.
[Para justificar os superscritos $-$
e $+$
você pode imaginar que os nós são contas bancárias
e os arcos representam movimentação de dinheiro.
Assim, tudo que sai de uma conta é subtraído do saldo
e tudo que entra é somado.]
É claro que $\cutout(R) = \cutin(\compl{R})$.
É claro também que
$\cutout(\emptyset) = \text{}$
$\cutout(V) = \text{}$
$\cutin(\emptyset) = \text{}$
$\cutin(V) = \emptyset$.
Se $v$ é um nó, usamos as abreviaturas $\cutout(v)$ e $\cutin(v)$ para $\cutout(\conj{v})$ e $\cutin(\conj{v})$ respectivamente. O número $|\cutout(v)|$ é o grau de saída de $v$ e o número $|\cutin(v)|$ é o grau de entrada de $v$. É claro que $|\cutout(v)| \leq n-1$ e $|\cutin(v)| \leq n-1$. É claro também que \[\textstyle \sum_{v\in V} |\cutout(v)| \ = \ \sum_{v\in V} |\cutin(v)| \ = \ m\text{.} \]
Um corte (= cut) em um grafo dirigido $(V,E)$ é o conjunto de todos os arcos que saem de algum conjunto de nós. Em outras palavras, um corte é qualquer conjunto da forma $\cutout(R)$, com $R\subseteq V$. (Pode parecer que um corte deveria ser definido como $\cutout(R) \cup \cutin(R)$, mas a definição que adotamos é mais útil.) O conjunto $R$ é a margem negativa do corte $\cutout(R)$ e $\compl{R}$ é a margem positiva.
Um corte $\cutout(R)$ é dirigido (= directed) se $\cutin(R) = \emptyset$.
Uma rede (= network) é um grafo dirigido juntamente com uma ou mais funções que atribuem números aos arcos e/ou aos nós do grafo. O conceito é propositalmente vago. Às vezes, a especificação de uma rede inclui a designação de um ou dois nós que desempenham um papel especial no problema que está sendo estudado.
Por exemplo, se $D$ é um grafo dirigido e $c$ é uma função de $E(D)$ em $\R$, podemos dizer que $(D,c)$ é uma rede. Da mesma forma, se $b$ é uma função de $V(D)$ em $\R$, podemos dizer que $(D,b,c)$ é uma rede.
A matriz de adjacências de um grafo dirigido tem linhas e colunas indexadas pelos nós. A componente da matriz na posição $(v,w)$ vale $1$ se $vw$ é um arco e vale $0$ em caso contrário.
A matriz de incidências tem linhas indexadas pelos nós e colunas indexadas pelos arcos. A coluna que corresponde a um arco $vw$ tem um $-1$ na linha $v$ e um $+1$ na linha $w$, sendo o resto da coluna igual a $0$. [Alguns livos adotam a convenção contrária: $+1$ na linha $v$ e $-1$ na linha $w$.] Portanto, a linha $v$ da matriz tem um $-1$ na coluna correspondente a cada arco que sai de $v$, um $+1$ na coluna correspondente a cada arco que entra em $v$, e $0$ nas demais colunas.
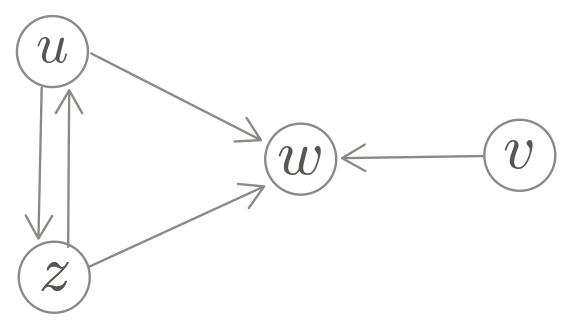
Exemplo F.3:
Seja $D$ o grafo dirigido com nós $u \ v \ w \ z$ \ e arcos
$uw \ vw \ zu \ uz \ zw$\,.
A matriz de adjacências de $D$ está representada à esquerda
(com $-$
representando $0$
)
e a matriz de incidências de $D$ está representada no meio:
Exemplo F.4: Veja à esquerda a matriz de adjacências de uma árvore orientada com nós $a \ b \ c \ d \ e \ f$. À direita, uma árvore radicada com o mesmo conjunto de nós e raiz $c$. (Faça figuras.)
Lema F.4 (ciclos e dependência linear) Seja $A$ a matriz de incidências de um grafo dirigido $D$. O conjunto das colunas de $A$ é linearmente dependente se e somente se $D$ tem um ciclo (não necessariamente dirigido).
Prova do somente se
:
Suponha que o conjunto das colunas de $A$ é l.d..
Seja $x$ um vetor real não nulo
tal que $Ax=0$.
Seja $F$ o conjunto $\conj{e\in E(D) : x_e \neq 0}$ e
considere o grafo induzido $D[F]$.
Seja $G$ o grafo não-dirigido subjacente a $D[F]$.
Como $Ax=0$,
nenhuma linha da matriz $A[\all,F]$ tem exatamente um elemento não nulo.
Portanto,
nenhum nó de $G$ tem grau $1$.
De acordo com o lema E.1,
$G$ tem um ciclo.
Logo, $D[F]$ tem um ciclo e portanto $D$ tem um ciclo.
Prova do se
:
Suponha que $D$ tem um ciclo, digamos
$\seq{v_0,e_1,v_1,\ldots, e_p,v_p}$.
Defina o vetor $x$
da seguinte maneira:
para cada índice $i$,
se $e_i$ é um arco direto do ciclo então $x_{e_i}=+1$,
se $e_i$ é um arco inverso então $x_{e_i}=-1$,
e se $e$ não pertence ao ciclo então $x_e=0$.
Observe que $Ax=0$.
Isso mostra que o conjunto das colunas de $A$ é l.d.. ■
Exemplo F.5: A figura mostra a matriz de incidências de um grafo dirigido que consiste em um ciclo simples e nada mais.
Corolário F.5 (florestas e independência linear) Seja $A$ a matriz de incidências de um grafo dirigido $D$. O conjunto das colunas de $A$ é linearmente independente se e somente se $D$ é uma floresta orientada (não necessariamente radicada). ■