Apêndice B
Poliedros
Embora pertençam ao mundo discreto,
problemas de otimização combinatória
têm aspectos contínuos e geométricos que é importante explorar.
B.1 O que é um poliedro?
Um poliedro é qualquer conjunto da forma $\conj{x : Ax \leq b}$
em que $x$ e $b$ são vetores e $A$ é uma matriz.
Mais precisamente, dado um conjunto finito $E$,
um poliedro
(= polyhedron)
no espaço $\R^E$ é o conjunto de todos os vetores reais
indexados por $E$ que satisfazem as restrições
\begin{equation}\label{def:polyhedron}
Ax \leq b\,\text{,}
\end{equation}
sendo $b$ um vetor real
indexado por algum conjunto $V$
e $A$ uma matriz real indexada por $V\times E$.
[Poderíamos nos restringir aos vetores e matrizes
racionais,
uma vez que computadores digitais desconhecem números irracionais.]
Em geral, o mesmo poliedro pode ser representado por muitos
pares $(A,b)$ diferentes.
Os exemplos abaixo mostram que
essa definição é suficientemente flexível
para acomodar restrições aparentemente diferentes
das especificadas em \eqref{def:polyhedron}.
Exemplo B.1:
Considere a matriz $A$ e o vetor $b$ representados abaixo,
com o vetor $b$ na vertical à direita da matriz $A$.
\[
\begin{array}{ccccc@{\hspace{3ex}}c}
11& 12& 13& 14& 15& 16\\
21& 22& 23& 24& 25& 26\\
31& 32& 33& 34& 35& 36\\
41& 42& 43& 44& 45& 46
\end{array}
\]
O poliedro $\conj{x : Ax \leq b}$
é o conjunto de todos os vetores $(x_1, x_2, x_3, x_4, x_5)$ que
satisfazem o sistema de desigualdades:
\[
\begin{split}
11x_1 + 12 x_2 + 13 x_3 + 14 x_4 + 15 x_5 \ &\leq \ 16\\
21x_1 + 22 x_2 + 23 x_3 + 24 x_4 + 25 x_5 \ &\leq \ 26\\
31x_1 + 32 x_2 + 33 x_3 + 34 x_4 + 35 x_5 \ &\leq \ 36\\
41x_1 + 42 x_2 + 43 x_3 + 44 x_4 + 45 x_5 \ &\leq \ 46
\end{split}
\]
Exemplo B.2:
O conjunto de todos os vetores $(x_1,x_2)$ que satisfazem
o sistema de desigualdades abaixo é um poliedro.
(Todos os coeficientes são inteiros, mas isso é irrelevante.)
\[
\begin{array}[b]{rcr@{\quad}c@{\enspace}c}
1x_1 &+& 3x_2 & \leq & 18\\
1x_1 &+& 0x_2 & \leq & 6\\
1x_1 &-& 2x_2 & \leq & 2\\
-1x_1 &-& 1x_2 & \leq & -5\\
-2x_1 &+& 1x_2 & \leq & -1\\
& & & & % hack
\end{array}
\]
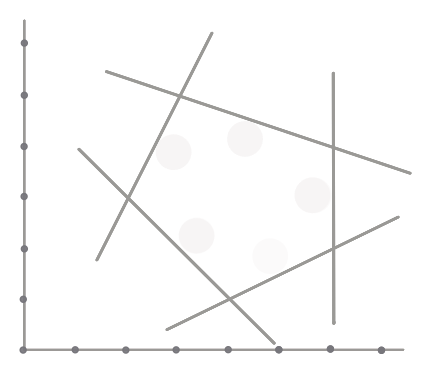
Exemplo B.3:
As figuras abaixo sugerem dois poliedros
em $\R^E$ com $E=\conj{1,2,3}$.
Exemplo B.4:
Seja $P$
o conjunto de todos os vetores $(x_1,x_2,x_3)$
que satisfazem o sistema de desigualdades abaixo.
Esse sistema é equivalente ao que aparece em seguida
e tem a forma especificada
na definição \eqref{def:polyhedron}.
Portanto, $P$ é um poliedro.
Em notação matricial, o poliedro é definido por $Ax \leq b$,
sendo $A$ e $b$ a matriz e o vetor exibidos na última parte da figura.
\[
\begin{array}[t]{*{5}{r}@{\enspace}c@{\enspace}r}
x_1 & & & & & \geq & 1\\
& & x_2 & & & \geq & 2\\
x_1 &+& x_2 & & & \leq & 5\\
x_1 &+& 2x_2 & & & \geq & 0\\
x_1 &+& x_2 &+& x_3 & \leq & 9\\
& & & & x_3 & = & 3
\end{array}
\]
\[
\begin{array}[t]{*{5}{r}@{\enspace}cr}
-x_1 & & & & & \leq & -1\\
& & -x_2 & & & \leq & -2\\
x_1 &+& x_2 & & & \leq & 5\\
-x_1 &-& 2x_2 & & & \leq & 0\\
x_1 &+& x_2 &+& x_3 & \leq & 9\\
& & & & x_3 & \leq & 3\\
& & & & -x_3 & \leq & -3
\end{array}
\]
\[
\begin{array}[t]{*{3}{r}r}
-1 & 0 & 0 & \enspace -1 \\
0 & -1 & 0 & -2 \\
1 & 1 & 0 & 5 \\
-1 & -2 & 0 & 0 \\
1 & 1 & 1 & 9 \\
0 & 0 & 1 & 3 \\
0 & 0 & -1 & -3
\end{array}
\]
As restrições que definem um poliedro não precisam ser
independentes entre si.
Nesse exemplo, a quarta e a quinta desigualdades
do sistema à esquerda
são redundantes:
o poliedro não se altera se essas desigualdades forem apagadas.
Exemplo B.5:
Seja $A$ uma matriz indexada por
$V\times E$ e $c$ um vetor indexado por $E$.
O conjunto de todos os vetores $y$ que satisfazem as restrições
$yA \leq c$ é igual ao conjunto
$\conj{y: \tr{A} y \leq c}$,
onde $\tr{A}$ a matriz transposta de $A$.
Como o último conjunto tem a forma especificada
na definição \eqref{def:polyhedron},
$\conj{y : yA \leq c}$ é um poliedro.
Exercícios B.1
-
Mostre que o conjunto de todos os vetores $x$ que satisfazem as restrições
$Ax \geq b$ é um poliedro.
-
Mostre que o conjunto de todos os vetores $x$ que satisfazem as restrições
$Ax = b$ é um poliedro.
-
Mostre que o conjunto de todos os vetores $x$ que satisfazem as restrições
$Ax \leq b$ e
$x \geq 0$
é um poliedro.
B.2 Vértices de poliedros
Os vetores mais interessantes de um poliedro estão da fronteira
,
ou casca
, do poliedro.
Esses vetores satisfazem de maneira justa
(isto é, com $=$
no lugar de $\leq$
)
uma ou mais das restrições que definem o poliedro.
Dentre esses vetores, os mais relevantes são os bicos
,
que definiremos de uma maneira geometricamente natural.
Um vetor $x$ de um poliedro $P := \conj{x : Ax \leq b}$
no espaço $\R^E$
é extremo
se não existe vetor $\d\neq 0$
tal que $x+\d$ e $x-\d$ estão ambos em $P$.
Os vetores extremos de um poliedro também são conhecidos como
vértices.
O conceito de vértice não está restrito a poliedros.
Ele se aplica também
a qualquer subconjunto convexo (veja o apêndice D)
de $\R^E$.
Exemplo B.6:
Considere o conjunto de todos os vetores $(x_1,x_2)$
que satisfazem as desigualdades a seguir.
(Faça uma figura.)
\[
\begin{array}[t]{rcl}
x_1 + x_2 &\leq& 2 \\[0.5ex]
-x_1 + x_2 &\leq& 0
\end{array}
\]
O vetor $(+1,+1)$ é um vértice nesse conjunto.
Exemplo B.7:
Considere o conjunto
de todos os vetores $(x_1,x_2)$
que satisfazem as restrições a seguir.
\[
\begin{array}[t]{rcl}
x_1 + x_2 &\leq& 3 \\[0.5ex]
x_1 - x_2 &\geq& 0 \\[0.5ex]
x_2 &\geq& 0
\end{array}
\]
Os vértices desse conjunto
são $(0,0)$,
$(\frac{3}{2},\frac{3}{2})$
e $(3,0)$.
(Faça uma figura.)
Exemplo B.8:
Para a matriz $A$ e o vetor $b$ definidos abaixo,
considere o poliedro $\conj{x: Ax \leq b}$.
\[
\begin{array}[t]{l@{\quad\enspace}rrr}
&1 &\ph{-}2 &\ph{-} 4 \\
A &1 & 2 & 5 \\
&1 & 2 & 6 \\[0.8ex]
x &3 & 2 & 0 \\[0.8ex]
\d &1 & -1 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{l@{\quad}r}
& 8 \\
b & 9 \\
& 10
\end{array}
\]
O vetor $x$ e os vetores $x+\d$ e $x-\d$ estão no poliedro.
Portanto, $x$ não é vértice do poliedro.
Exemplo B.9:
Nem todo poliedro tem vértices.
Considere o poliedro $P := \conj{x: Ax \leq b}$,
com $A$ e $b$ dados a seguir.
(Faça uma figura.)
\[
\begin{array}[t]{l@{\quad\enspace}rr}
A &+1 &+1 \\[0.8ex]
\d &+1 & -1
\end{array}
\hspace{6ex}
\begin{array}[t]{l@{\quad\enspace}r}
b & 2
\end{array}
\]
Para qualquer $x$ em $P$,
tanto $x+\d$ quanto $x-\d$ estão em $P$.
Exemplo B.10:
Seja $P$ o poliedro definido pelas desigualdades $Ax \leq b$.
Seja $\xhat$ um vetor de $P$ tal que $A\xhat = b$.
Suponha que $\xhat$ não é vértice de $P$.
Então existe um vetor não nulo $\d$ tal que
$A(\xhat+\d) \leq b$ e $A(\xhat-\d)\leq b$.
Segue daí que
\[
A\d = 0
\]
e portanto o conjunto das colunas de $A$ é
linearmente dependente.
Lema B.1 (caracterização dos vértices)
Seja $A$ uma matriz indexada por $V\times E$ e
$b$ um vetor indexado por $V$.
Seja $x$ um vetor do poliedro $P := \conj{x : Ax \leq b}$
e $I(x)$ o conjunto de todos os índices $i$ em $V$ tais que
\[
A[i,\all]x = b[i]\text{.}
\]
O vetor $x$ é vértice de $P$
se e somente se o conjunto das colunas da matriz $A[I(x),\all]$ é
linearmente independente.
Prova do se
:
Suponha que $x$ não é vértice do poliedro.
Então existe um vetor não nulo $\d$
tal que $Ax + A\d \leq b$ e $Ax - A\d \leq b$.
Para cada $i$ em $I(x)$, temos
\[
b[i] + A[i,\all]\d \leq b[i] \quad \text{e} \quad
b[i] - A[i,\all]\d \leq b[i]\text{,}
\]
uma vez que $A[i,*]x=b[i]$.
Portanto, $A[i,\all]\d=0$ para cada $i$.
Logo, o conjunto das colunas de $A$ é l.d..
Em particular, o conjunto das colunas de $A[I(x),\all]$ é l.d..
Prova do somente se
:
Suponha que o conjunto das colunas de $A[I(x),\all]$ é l.d..
Então existe um vetor não nulo $\d$ indexado por $E$ tal que
$A[I(x),\all] \d = 0$.
Logo,
\[
A[I(x),\all](x \pm \d) \leq b[I(x)]\text{.}
\]
Por outro lado, $A[h,\all]x \lt b[h]$ para cada $h$ em $V\setm I(x)$.
Logo, para algum número positivo $\epsilon$ suficientemente pequeno
temos
\[
A[V\setm I(x),\all](x \pm \epsilon \d) \leq b[V\setm I(x)]\text{.}
\]
Em suma, $A(x \pm \epsilon \d) \leq b$ e
portanto $x$ não é vértice de $P$. ■
O lema poderia ser enunciado assim:
$x$ é vértice do poliedro se e somente se o posto
da matriz $A[I(x),E]$ é $|E|$.
Em outras palavras, $x$ é vértice se e somente se
o posto de colunas da matriz $A[I(x),E]$ é pleno
,
e assim $x$ é a única solução do sistema de equações $A[I(x),E]x= b[I(x)]$.
Exemplo B.11:
O lado esquerdo da figura abaixo mostra uma matriz $A$,
um vetor $b$ (à direita da matriz),
e um vetor $\xhat$ (abaixo da matriz).
Seja $I(\xhat)$ o conjunto
das $6$ primeiras linhas de $A$.
Então $A[i,\all]\xhat=b[i]$ se e somente se $i\in I(\xhat)$.
Observe que o conjunto das colunas de $A[I(\xhat),\all]$ é l.i..
(Portanto, o conjunto das colunas de $A$ também é l.i..)
O vetor $\xhat$ é vértice do poliedro $Ax \leq b$.
\[
\begin{array}{rrrr@{\qquad}r}
1 & 0 & 0 & 0 & 2 \\
0 & 1 & 0 & 0 & 3 \\
0 & 0 & 1 & 0 & 4 \\
0 & 0 & 0 & 1 & 5 \\
1 & 1 & 0 & 0 & 5 \\
3 & 3 & 3 & 3 & 42 \\
0 & 0 & 2 & 0 & 10 \\
0 & 0 & 0 & 4 & 30 \\[1.5ex]
2 & 3 & 4 & 5 &
\end{array}
\qquad\qquad\qquad
\begin{array}{rrrr@{\qquad}r}
1 & 0 & 0 & 0 & 3 \\
0 & 1 & 0 & 0 & 4 \\
0 & 0 & 1 & 0 & 5 \\
0 & 0 & 0 & 1 & 6 \\
3 & 1 & 0 & 0 & 9 \\
3 & 1 & 0 & 1 & 14 \\
3 & 1 & 1 & 0 & 13 \\
3 & 1 & 1 & 1 & 18 \\[1.5ex]
2 & 3 & 4 & 5 &
\end{array}
\]
Agora considere os objetos $A$, $b$ e $\xhat$ do lado direito da figura.
Seja $I(\xhat)$ o conjunto
das $4$ últimas linhas de $A$.
Então $A[i,\all]\xhat=b[i]$ se e somente se $i\in I(\xhat)$.
Embora o conjunto das colunas de $A$ seja l.i.,
o conjunto das colunas de $A[I(\xhat),\all]$ é l.d..
Portanto, o vetor $\xhat$ não é vértice do poliedro $Ax \leq b$.
Exemplo B.12:
Considere novamente o poliedro $P$ do exemplo B.4.
Veja abaixo, mais uma vez,
o sistema de desigualdades que define $P$.
O subsistema formado pela primeira, segunda e sexta desigualdades
(veja a coluna esquerda da segunda parte da figura)
é satisfeito com igualdade pelo vetor $(1,2,3)$ e por nenhum outro.
Esse vetor pertence a $P$
e portanto é um vértice de $P$.
\[
\begin{array}[t]{*{5}{r}@{\quad}c@{\quad}r}
x_1 & & & & & \geq & 1\\
& & x_2 & & & \geq & 2\\
x_1 &+& x_2 & & & \leq & 5\\
x_1 &+& 2x_2 & & & \geq & 0\\
x_1 &+& x_2 &+& x_3 & \leq & 9\\
& & & & x_3 & = & 3
\end{array}
\]
\[
\begin{array}[t]{*{5}{r}@{\enspace}c@{\enspace}r}
x_1 & & & & & = & 1\\
& & x_2 & & & = & 2\\
% & & & & & & \\
% & & & & & & \\
% & & & & & & \\
& & & & x_3 & = & 3
\end{array}
\hspace{4ex}
\begin{array}[t]{*{5}{r}@{\enspace}c@{\enspace}r}
x_1 & & & & & = & 1\\
% & & & & & & \\
x_1 &+& x_2 & & & = & 5\\
% & & & & & & \\
% & & & & & & \\
& & & & x_3 & = & 3
\end{array}
\]
O subsistema formado pela primeira, terceira e sexta desigualdades
(veja a coluna direita da segunda parte da figura)
é satisfeito com igualdade apenas por $(1,4,3)$.
Esse vetor pertence a $P$
e portanto é um vértice de $P$.
Analogamente, o subsistema formado pela segunda, terceira e sexta desigualdades
define o vértice $(3,2,3)$.
Esses são os três únicos vértices de $P$.
Agora veja alguns subsistemas que não definem vértices.
O subsistema formado pela primeira, quarta, e sexta desigualdades
é satisfeito com igualdade apenas pelo vetor $(1,-\frac{1}{2},3)$,
mas esse vetor não pertence a $P$.
O subsistema formado pela primeira, segunda, terceira e sexta desigualdades
não é satisfeito com igualdade por nenhum vetor.
O subsistema formado pela primeira e segunda desigualdades
é satisfeito com igualdade por mais de um
vetor.
Corolário B.2
O poliedro $\conj{x : Ax \leq b}$ tem um vértice se e somente se
$A$ tem posto igual ao número de colunas. ■
Corolário B.3
O número de vértices do poliedro $\conj{x : Ax \leq b}$ é finito. ■
Exercícios B.2
-
Complete os detalhes da prova do lema B.1.
-
Prove o corolário B.2.
-
Prove o corolário B.3.
-
★
Seja $Q$ o poliedro $\conj{y : yA \leq c}$,
onde $A$ é uma matriz indexada por $V\times E$ e $c$ um vetor indexado por $E$.
Seja $y$ um vetor de $Q$ e considere o conjunto de índices
$J(y) = \conj{j\in E : yA[\all,j] = c[j]}$.
Mostre que $y$ é vértice de $Q$
se e somente se o conjunto das linhas da matriz $A[\all,J(y)]$ é l.i..
-
★
Seja $P$ o poliedro $\conj{x : Ax \leq b \text{ e } x \geq 0}$,
onde $A$ é uma matriz indexada por $V\times E$ e $b$ um vetor indexado por $V$.
Seja $x$ um vetor de $P$ e considere os conjuntos de índices
$I(x) = \conj{i\in V : A[i,\all]x = b[i]}$
e
$J(x) = \conj{j\in E : x[j] = 0}$.
Mostre que $x$ é vértice de $P$
se e somente se o conjunto das colunas da matriz $A[I(x),E\setm J(x)]$ é l.i..
-
★
Seja $P$ o poliedro $\conj{x : Ax = b \text{ e } x \geq 0}$,
onde $A$ é uma matriz indexada por $V\times E$ e $b$ um vetor indexado por $V$.
Seja $x$ um vetor de $P$ e considere o conjunto de índices
$J(x) = \conj{j\in E : x[j] = 0}$.
Mostre que $x$ é vértice de $P$
se e somente se o conjunto das colunas da matriz $A[V,E\setm J(x)]$ é l.i..
B.3 Poliedros limitados
Um poliedro $P$ é limitado (= bounded)
se existem vetores $l$ e $u$ em $\R^E$ tais que $l \leq x \leq u$
para todo $x$ em $P$.
Em termos informais, um poliedro é limitado se cabe
em um cubo.
Um poliedro é ilimitado
(= unbounded)
se não for limitado.
Exemplo B.13:
Considere o conjunto de todos os vetores $(x_1,x_2)$ que satisfazem
as desigualdades abaixo. (Faça uma figura.)
Esse poliedro é ilimitado.
\[
\begin{array}{rcl}
x_1 - x_2 &\leq& 4\\
x_1 - x_2 &\geq& 2
\end{array}
\]
Exemplo B.14:
Considere novamente o poliedro do exemplo B.4.
Trata-se do conjunto de todos os vetores $(x_1,x_2,x_3)$
que satisfazem o sistema de desigualdades abaixo.
Esse poliedro é limitado pois $0\leq x_i\leq 5$ para todo $i$.
(Verifique!)
\[
\begin{array}[t]{*{5}{r}@{\enspace}c@{\enspace}r}
x_1 & & & & & \geq & 1\\
& & x_2 & & & \geq & 2\\
x_1 &+& x_2 & & & \leq & 5\\
x_1 &+& 2x_2 & & & \geq & 0\\
x_1 &+& x_2 &+& x_3 & \leq & 9\\
& & & & x_3 & = & 3
\end{array}
\]
Lema B.4
Todo poliedro limitado não vazio tem pelo menos um vértice.
Esboço da prova:
Seja $\conj{x : Ax \leq b}$ um poliedro limitado
e $x$ um vetor do poliedro.
Seja $I(x)$ o conjunto dos índices $i$ tais que $A[i,\all]x=b[i]$.
Se $x$ não é vértice,
então existe um vetor não nulo $\d$
tal que $x+\d$ e $x-\d$ estão no poliedro.
Seja $\epsilon$ o maior número positivo tal que $x+\epsilon \d$
está no poliedro.
Um tal $\epsilon$ está bem definido pois o poliedro é limitado.
Seja $x'$ o vetor $x+\epsilon \d$.
O conjunto de índices $i$ para os quais
$A[i,\all]x' = b[i]$
é um superconjunto próprio de $I(x)$.
Repita o processo com $x'$ no papel de $x$.
Depois de um número finito de iterações, teremos um vértice. ■
A recíproca do lema não é verdadeira:
muitos poliedros ilimitados têm vértices.
Por exemplo, o vetor $0$ é vértice do poliedro definido pelas desigualdades
$x\geq 0$.
Poliedros inteiros
Um poliedro limitado é inteiro
(= integral)
se todos os seus vértices forem vetores inteiros.
Poliedros limitados inteiros têm especial importância
em otimização combinatória.
Exercícios B.3
-
Prove o lema B.4.
-
Seja $P$ um poliedro não necessariamente limitado.
Suponha que $x\geq 0$ para todo $x$ em $P$.
Mostre que $P$ tem um vértice.
[CCPS 6.3]