Capítulo 6
Emparelhamentos
Este capítulo introduz o conceito de emparelhamento
em um grafo
e enuncia três problemas básicos envolvendo
emparelhamentos.
O capítulo também mostra como resolver esses problemas em grafos bipartidos.
A solução dos problemas em grafos arbitrários
ficará a cargo dos capítulos seguintes.
Todos os grafos neste capítulo
são não-dirigidos.
Por isso, diremos simplesmente grafo
,
deixando o
não-dirigido
subentendido.
Consulte o
índice remissivo
e os apêndices
para conferir as definições de termos técnicos.
6.1 Emparelhamentos
Um emparelhamento
(= matching)
num grafo $G$
é um conjunto $M$ de arestas
que incide
no máximo uma vez
em cada nó de $G$.
Em outras palavras,
um conjunto $M$ de arestas é um emparelhamento
se cada nó do
grafo $(V(G),M)$
tem grau $0$
ou grau $1$.
[Em biologia molecular,
emparelhamentos
são conhecidos como alinhamentos.]
Dizemos que um emparelhamento $M$
satura um nó $v$
se $v$ é ponta de alguma aresta de $M$.
Se $M$ não satura $v$, dizemos que $v$ está
exposto por $M$,
ou
$M$-exposto.
Todo emparelhamento $M$ deixa exatamente
$|V(G)|-2|M|$
nós expostos.
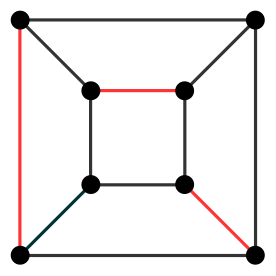
Exemplo 6.1:
No grafo da figura, o conjunto de arestas vermelhas é um
emparelhamento.
O emparelhamento
satura 6 nós e deixa 2 nós expostos.
Exemplo 6.2:
Suponha dado um conjunto de operários,
um conjunto de máquinas, e
o conjunto de todos os pares $(o,m)$
tais que o operário $o$ está habilitado a operar
a máquina $m$.
Queremos encontrar um casamento
de $k$ operários
com $k$ máquinas
(supondo que cada operário pode operar apenas uma máquina
e cada máquina deve ser operada por apenas um operário).
Em que condições um tal casamento
existe?
Exemplo 6.3:
Uma companhia de aviação opera aviões que precisam
ser tripulados por dois pilotos.
Por algum motivo, alguns pares de pilotos são incompatíveis,
isto é, não podem voar junto.
Queremos encontrar um conjunto máximo de pares de pilotos
mutuamente compatíveis.
6.2 Três problemas
Encontrar um emparelhamento
pequeno num grafo é muito fácil:
o conjunto vazio, por exemplo,
é um emparelhamento.
É bem mais difícil encontrar um
emparelhamento
grande.
Um emparelhamento $M$ é máximo
se tem cardinalidade máxima,
ou seja,
se não existe emparelhamento
$M'$ tal que $|M'| > |M|$.
É claro que um emparelhamento é máximo
se e somente se minimiza o número de nós expostos.
Problema 6.A (emparelhamento máximo)
Encontrar um
emparelhamento
máximo num grafo.
É importante esclarecer desde já a diferença entre máximo
e maximal
.
Um emparelhamento
$M$ é maximal
se não é subconjunto próprio
de outro
emparelhamento,
ou seja,
se não existe emparelhamento
$M'$ tal que $M' \supset M$.
Todo
emparelhamento
máximo é maximal,
mas a recíproca está longe de ser verdadeira.
Por exemplo, o
emparelhamento
vermelho do
exemplo 6.1
é maximal mas não é máximo.
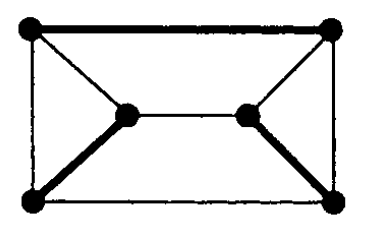
Exemplo 6.4:
A figura mostra um
emparelhamento com $4$ arestas.
Esse
emparelhamento é máximo pois
o gradfo não tem emparelhamento
com $5$ ou mais arestas.
Um tipo especial de emparelhamento máximo
tem um papel importante na solução do problema 6.A:
trata-se do emparelhamento
perfeito.
Um emparelhamento
é perfeito
se satura todos os nós do grafo,
ou seja, se não deixa nós expostos.
Exemplo 6.5:
O conjunto de linhas grossas é um
emparelhamento perfeito.
É claro que num grafo com $n$ nós
um emparelhamento é perfeito
se e somente se tem $n/2$ arestas
(o que significa, em particular, que $n$ é par).
Problema 6.B (emparelhamento perfeito)
Encontrar um emparelhamento
perfeito num grafo.
Finalmente, é útil considerar uma generalização
do problema 6.B que fica satisfeita com um
emparelhamento
suficientemente grande:
Problema 6.C (emparelhamento grande)
Dado um número
natural $k$,
encontrar um
emparelhamento
com $k$ arestas num grafo.
Pode parecer que esse enunciado não deixa claro se o
emparelhamento
deve ter exatamente $k$ arestas
ou pelo menos $k$ arestas.
Mas essa distinção é irrelevante,
uma vez que todo emparelhamento
com mais de $k$ arestas
contém um emparelhamento
com exatamente $k$ arestas.
Exercícios 6.2
-
Mostre que um emparelhamento $M$
num grafo é máximo
se e somente se $|M| \geq |M'|$ para qualquer outro
emparelhamento $M'$.
-
Mostre que todo emparelhamento
num grafo com $n$ nós
tem no máximo $\floor{n/2}$ arestas.
Mostre que qualquer emparelhamento
com $\floor{n/2}$ arestas é máximo.
-
Suponha dado um algoritmo AlgA
para o problema
problema 6.A.
É possível usar AlgA para resolver o
problema 6.B?
É possível usar AlgA para resolver o
problema 6.C?
-
Suponha dado um algoritmo AlgB
para o problema
problema 6.B.
O algoritmo devolve um emparelhamento perfeito
ou informa que o grafo não tem
emparelhamento perfeito.
É possível usar AlgB para resolver o
problema 6.A?
É possível usar AlgA para resolver o
problema 6.C?
-
Suponha dado um algoritmo AlgC
para o problema
problema 6.C.
O algoritmo recebe um grafo $G$ e um número $k$
e devolve um emparelhamento de tamanho $k$
ou informa que um tal emparelhamento não existe.
É possível usar AlgC para resolver o
problema 6.A?
É possível usar AlgC para resolver o
problema 6.B?
6.3 Caminhos alternantes e o teorema de Berge
Uma ferramenta essencial para a resolução de qualquer dos
três problemas sobre
emparelhamentos
é o caminho alternante.
Dado um emparelhamento
$M$ num grafo,
um caminho alternante
é qualquer caminho
simples
cujas arestas estão alternadamente em $M$ e fora de $M$.
Um caminho alternante $P$ é aumentador
(= augmenting),
ou de aumento,
se (1) $P$ tem pelo menos uma aresta
e (2) a origem e o témino de $P$ são
$M$-expostos.
Para ressaltar o papel de $M$,
podemos usar as expressões caminho $M$-alternante
e caminho $M$-aumentador.
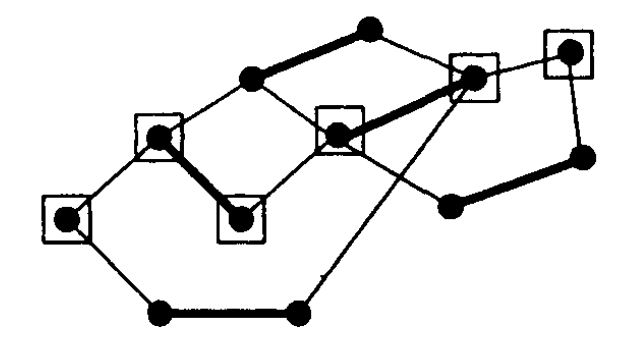
Exemplo 6.6:
As linhas grossas representam um
emparelhamento
no grafo.
Os quadrados destacam um caminho aumentador.
Um caminho $M$-aumentador permite transformar $M$ num
emparelhamento
maior.
Para realizar essa transformação,
usamos a operação de diferença simétrica.
A diferença simétrica
entre dois conjuntos $A$ e $B$
é o conjunto
$A\symdiff B \ := \ (A\setm B)\cup(B\setm A)$.
Se $P$ é um caminho $M$-aumentador
então $M\symdiff E(P)$ é um
emparelhamento
e esse emparelhamento
é maior que $M$.
Essa propriedade sugere um algoritmo iterativo
para encontrar um emparelhamento máximo.
Essa ideia esbarra em duas questões:
(1) Como encontrar um caminho aumentador?
e (2) Existe caminho $M$-aumentador
sempre que $M$ não é máximo?
Trataremos da primeira pergunta
no capítulo 7.
Quanto à segunda, ela foi respondida por C. Berge
em 1957:
Teorema 6.1 (de Berge)
Um emparelhamento $M$
é máximo se e somente se não existe caminho $M$-aumentador.
Prova do teorema:
Suponha que $P$ é um caminho $M$-aumentador.
Então $M\symdiff E(P)$ é um emparelhamento
e satura todos os nós saturados por $M$ e mais dois.
Logo, $M$ não é máximo.
Suponha agora que um
emparelhamento $M$ não é máximo.
Então existe um emparelhamento maior,
digamos $N$.
Cada nó do grafo é ponta de no máximo duas arestas
do conjunto $M\symdiff N$.
Portanto, cada componente conexa
do subgrafo induzido
por $M\symdiff N$
consiste em
um caminho simples ou
um circuito
(isto é, um ciclo simples).
Como $|N|>|M|$,
alguma componente é um caminho com mais arestas em $N$ que em $M$.
Esse caminho é $M$-aumentador. ■
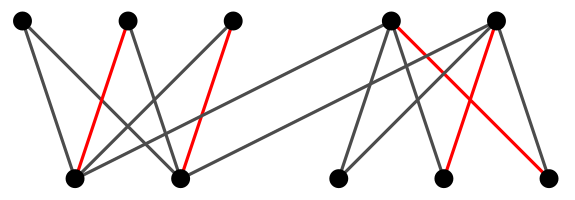
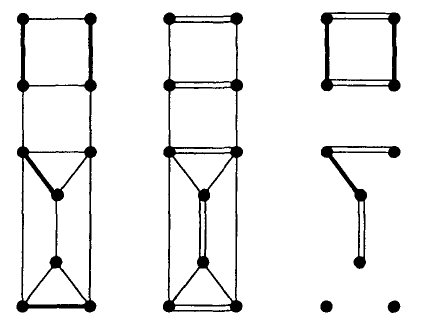
Exemplo 6.7:
A primeira parte da figura mostra um
emparelhamento $M$ (linhas grossas).
A segunda parte mostra um
emparelhamento $N$ (linhas duplas) no mesmo grafo.
A terceira parte mostra o subgrafo induzido por $M\symdiff N$.
Caminhos aumentadores para emparelhamentos
são análogos aos
caminhos de aumento para fluxo
da seção 2.4.
Mas algumas diferenças chamam a atenção:
lá os grafos eram dirigidos, enquanto aqui são não-dirigidos;
lá podíamos ter dois ou mais arcos consecutivos do mesmo tipo
(direto ou inverso),
enquanto aqui as arestas estão alternadamente
no emparelhamento
e fora dele.
Um fluxo $x$ é máximo se e somente se
não existe caminho de aumento para $x$.
Esse fato é análogo ao teorema 6.1.
Exercícios 6.3
-
Enuncie em separado as partes
se
e somente se
do teorema de Berge
(teorema 6.1).
-
Seja
$M^*$ um emparelhamento máximo
e $M$ um emparelhamento
qualquer em um grafo $G$.
Use o método de prova do teorema 6.1
para mostrar que $G$ tem pelo menos
$|M^*|-|M|$ caminhos $M$-aumentadores disjuntos
(ou seja, sem nós em comum).
[CCPS 5.2]
-
Seja $M$ um emparelhamento de tamanho $4000$
num grafo que tem um emparelhamento
de tamanho $5000$.
Use o resultado do exercício anterior
para mostrar que o grafo tem um caminho $M$-aumentador
de comprimento no máximo $9$.
[CCPS 5.3]
-
Sejam $M_1$ e $M_2$ dois emparelhamentos
em um grafo bipartido $G$
com bipartição $(P_1,P_2)$.
Mostre que existe um emparelhamento $N$
que satura todos os nós de $P_1$ saturados por $M_1$
e todos os nós de $P_2$ saturados por $M_2$.
[AMO 12.8]
-
Slither.
O jogo Slither é jogado por duas pessoas,
digamos Um e Dois,
sobre um grafo $G$.
Os jogadores se alternam:
o primeiro a jogar é Um,
o segundo é Dois, e assim por diante.
Cada jogada consiste em escolher uma aresta
de tal modo que, a cada passo,
o conjunto das arestas escolhidas forme um
caminho simples.
Perde o jogador que não puder fazer uma jogada válida.
Prove que Um pode forçar uma vitória se $G$ tiver um
emparelhamento perfeito.
[CCPS 5.18]
-
Slither.
Considere o jogo Slither do exercício acima.
Prove que Dois pode forçar uma vitória
se a primeira jogada de Um
for uma aresta $vw$ tal que $v$ não é saturado
por algum emparelhamento máximo.
[CCPS 5.19]
-
Cobertura mínima por arestas.
Uma cobertura por arestas
de um grafo $G$ é qualquer subconjunto $B$ de $E(G)$
que incide em cada nó de $G$
(ou seja, cada nó é ponta de alguma aresta de $B$).
Não confunda cobertura por arestas com a
cobertura por nós.
Todo emparelhamento
perfeito, por exemplo, é uma cobertura por arestas.
Seja $G$ um grafo sem nós
isolados
e mostre como uma cobertura mínima de $G$ por arestas
pode ser calculada a partir de um
emparelhamento máximo.
Prove que o tamanho
de uma cobertura mínima por arestas é $|V(G)|-|M^*|$,
sendo $M^*$ um emparelhamento máximo.
[CCPS 5.13]
6.4 Condições de existência de solução
Considere o problema 6.C
do emparelhamento grande.
Nem toda instância
do problema tem solução,
ou seja, nem todo grafo tem
um emparelhamento
de tamanho $k$.
Isso levanta a seguinte pergunta:
como certificar a inexistência de solução?
Como tornar evidente que o grafo em questão
não tem um emparelhamento
de tamanho $k$?
Uma tentativa de responder a pergunta
leva ao seguinte conceito.
Uma cobertura por nós
(= node cover)
de um grafo
é um conjunto $K$ de nós
tal que toda aresta do grafo tem pelo menos uma ponta
em $K$.
Quando não houver confusão, diremos cobertura
no lugar de cobertura por nós
.
Há uma relação óbvia entre coberturas e
emparelhamentos:
Lema 6.2
Para qualquer emparelhamento $M$
e qualquer cobertura $K$,
tem-se $|M| \leq |K|$. ■
O lema poderia ter sido formulado assim:
se existe uma cobertura com menos que $k$ nós
então não existe emparelhamento
com $k$ arestas.
Segue daí que uma cobertura com menos de $k$ nós
é um certificado da inexistência de um
emparelhamento
com $k$ arestas.
Essas considerações se aplicam também ao
problema 6.B
do emparelhamento perfeito.
Num grafo com $n$ nós,
uma cobertura com menos que $n/2$ nós
é um certificado da inexistência de um
emparelhamento perfeito.
O lema 6.2 também produz um certificado
para o problema 6.A
do emparelhamento máximo.
Dado um
emparelhamento $M$,
qualquer cobertura com exatamente $|M|$ nós
é um certificado da maximalidade de $M$.
Infelizmente, a recíproca do
lema 6.2
não é verdadeira:
muitos grafos sem emparelhamentos
grandes não têm coberturas pequenas.
Em particular,
muitos grafos sem emparelhamentos
perfeitos não têm coberturas menores que $n/2$.
Entretanto, a recíproca do lema 6.2 vale
em grafos bipartidos,
como veremos
na seção 6.5.
Exercícios 6.4
-
★
Prove o lema 6.2.
-
Suponha que um grafo $G$ tem uma cobertura com $\floor{n/2}$
nós, sendo $n := |V(G)|$.
Mostre que $G$ não tem emparelhamente perfeito.
-
★
Mostre que um emparelhamento
máximo num grafo
pode ser menor que uma cobertura mínima.
(Uma cobertura $K$ é mínima
se não existe cobertura $K'$ tal que $|K'| \lt |K|$.)
-
Mostre que todo grafo com $n$ nós tem uma cobertura com
apenas $n-1$ nós.
-
Seja $G$ um grafo bipartido com
bipartição $\conj{P,Q}$.
Mostre que tanto $P$ quanto $Q$ são coberturas.
Dê um exemplo para mostrar que $G$ pode ter uma
cobertura pequena com
alguns nós em $P$ e alguns em $Q$.
6.5 Grafos bipartidos
Todos os problemas que envolvem emparelhamentos
ficam mais fáceis quando restritos a
grafos
bipartidos.
Em particular,
a técnica desenvolvida no capítulo 2
para tratar de fluxos
é suficiente para resolver problemas de
emparelhamentos
em grafos bipartidos.
Emparelhamento grande.
Considere o problema 6.C.
De acordo com o lema 6.2,
uma condição necessária para a existência de um
emparelhamento grande
é que todas as coberturas também sejam grandes.
Vamos mostrar que essa condições também é suficiente
quando o grafo é bipartido.
Teorema 6.3
Num grafo bipartido,
se toda cobertura tem $k$ ou mais nós
então existe um emparelhamento
com $k$ ou mais arestas.
Esboço da prova:
Poderíamos usar a técnica dos
caminhos aumentadores
para provar o teorema.
Mas é mais instrutivo mostrar como o teorema decorre da
teoria do Fluxo Máximo e Corte Mínimo
da seção 2.4.
O primeiro passo é reduzir nosso problema ao problema de fluxo máximo
(problema 2.A).
Seja $G$ o grafo em questão e
seja $\conj{P,Q}$ uma bipartição de $G$.
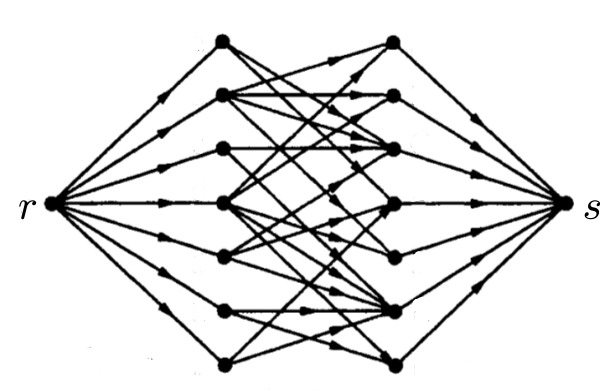
Construa uma rede capacitada
$(D,u)$ da seguinte maneira.
O conjunto de nós do grafo dirigido $D$ é $V(G)\cup\conj{r,s}$,
sendo $r$ e $s$ dois novos nós.
Os arcos de $D$
e suas capacidades
são definidos assim:
-
para cada $p$ em $P$, há um arco $rp$ com
capacidade $u_{rp}=1$;
-
para cada $q$ em $Q$, há um arco $qs$ com capacidade $u_{qs}=1$;
-
para cada aresta $pq$ com $p\in P$ e $q\in Q$,
há um arco $pq$ com capacidade $u_{pq}=\infty$.
(É bem verdade que a formulação do
problema do fluxo máximo
supõe que todas as capacidades são finitas,
mas podemos aceitar capacidades infinitas aqui sem fazer escândalo.)
Seja $R$ um conjunto de nós que separa $r$ de $s$ em $D$
(isto é, $r\in R$ e $s\notin R$)
e suponha que toda cobertura de $G$ tem $k$ ou mais nós.
Vamos mostrar que $\uout(R) \geq k$.
Para isso, considere o conjunto
\[
(P\setm R)\cup(Q\cap R)\,\text{.}
\]
Se esse conjunto é uma cobertura de $G$
então nenhuma aresta tem uma ponta em $P\cap R$ e outra em $Q\setm R$
e portanto
$\uout(R) = \text{}$ $|P\setm R|+|Q\cap R| \geq k$.
Se $(P\setm R)\cup(Q\cap R)$ não é um cobertura de $G$
então alguma aresta de $G$ tem uma ponta em $P\cap R$ e outra em $Q\setm R$,
donde $\uout(R) = \text{}$ $\infty > k$.
Em qualquer caso, $\uout(R) \geq k$ para todo $R$ que separa $r$ de $s$.
O teorema MFMC
(teorema 2.9 do capítulo 2)
garante então que
a rede $(D,u)$ tem um fluxo viável $x$
tal que $\intens(x) \geq k$.
De acordo com o teorema MFMC inteiro
(teorema 2.10),
podemos supor que $x$ é inteiro
e portanto binário.
O conjunto $M$ das arestas $pq$ de $G$ tais que $x_{pq}=1$
é então é um emparelhamento.
Ademais, $|M| = \intens(x) \geq k$. ■
A prova do teorema 6.3 sugere um algoritmo
que resolve a restrição do
problema 6.C
a grafos bipartidos.
O algoritmo recebe um grafo bipartido $G$ e um número $k$
e devolve
-
um emparelhamento de tamanho $k$
ou
-
uma cobertura de tamanho menor que $k$.
A cobertura serve de certificado
da inexistência de um
emparelhamento
de tamanho $k$.
Emparelhamento máximo.
É fácil deduzir do lema 6.2
e do teorema 6.3
o seguinte teorema min-max
de D. Kőnig
(1931):
Teorema 6.4 (de Kőnig)
Em qualquer grafo bipartido tem-se
$\max_M |M| = \text{}$ $\min_K |K|$,
sendo $\max_M$ tomado sobre todos os
emparelhamentos $M$
e $\min_K$ tomado sobre todas as
coberturas $K$. ■
A prova desse teorema sugere imediatamente um algoritmo
que resolve a restrição do
problema 6.A
a grafos bipartidos.
O algoritmo recebe um grafo bipartido $G$
e devolve
um emparelhamento de $M$
e uma cobertura $K$ de mesmo tamanho.
A cobertura serve de certificado
da maximalidade do emparelhamento.
Emparelhamento perfeito.
Num grafo bipartido, é natural substituir
o conceito de emparelhamento perfeito
pelo seguinte conceito de emparelhamento
semiperfeito
.
Dada uma bipartição
$\conj{P,Q}$ de um grafo $G$,
dizemos que um emparelhamento $M$
satura o lado $P$ da bipartição
se $M$ satura
todos os nós de $P$.
É claro que $M$ satura $P$ se e somente se $|M|=|P|$.
Uma interessante condição para a existência
de um emparelhamento que satura $P$
foi descoberta por
P. Hall.
Para formular a condição de Hall, usamos a seguinte notação:
para qualquer subconjunto $X$ de $P$,
denotamos por $N(X)$
o conjunto de todos os nós que são
vizinhos
de nós de $X$.
[A letra $N$ é a inicial de
neighborhood
(= vizinhança).]
É claro que $N(X)\subseteq Q$.
Teorema 6.5 (de Hall)
Em qualquer grafo bipartido
com bipartição $\conj{P,Q}$,
existe um emparelhamento
que satura $P$
se e somente se
$|N(X)| \geq |X|$
para cada subconjunto $X$ de $P$. ■
É um ótimo exercício deduzir esse teorema do
teorema 6.3.
Exercícios 6.5
-
★
Complete os detalhes da prova do
teorema 6.3.
-
Na prova do teorema 6.3,
por que não adotar a
função-capacidade
$u=1$?
Por que não definir as capacidades assim:
$u_{pq}= 1$ para cada aresta $pq$ de $G$,
$u_{rp}= \infty$ para cada $p$ em $P$ e
$u_{qs}= \infty$ para cada $q$ em $Q$?
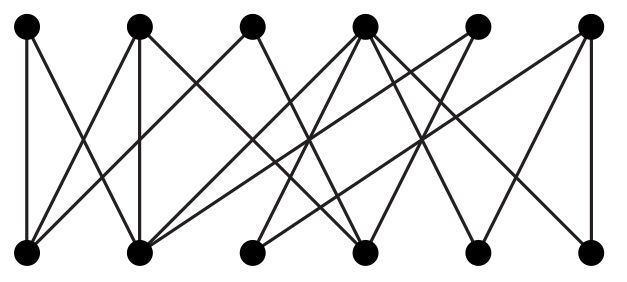
-
Encontre um emparelhamento
máximo e uma cobertura mínima no grafo da figura.
-
★
Prove o teorema 6.4
a partir do teorema 6.3
e do lema 6.2.
-
Seja $G$ um grafo com bipartição $\conj{P,Q}$.
Mostre que um emparelhamento $M$ satura $P$
se e somente se $|M|=|P|$.
-
Seja $M$ um emparelhamento perfeito em um grafo bipartido $G$.
Escolha uma das pontas de cada aresta de $M$.
Seja $K$ o conjunto dos nós escolhidos.
É verdade que $K$ é uma cobertura por nós de $G$?
-
Enuncie em separado as partes
se
e somente se
do teorema de Hall
(teorema 6.5).
Deduza do teorema 6.3
a parte se
do teorema de Hall.
-
Emparelhamento perfeito.
Seja $G$ um grafo com bipartição $\conj{P,Q}$.
Prove que $G$ tem um
emparelhamento perfeito
se e somente se
$|N(X)| \geq |X|$ para todo $X\subseteq P$ e todo $X\subseteq Q$.
(Dica: Veja o teorema de Hall.)
-
Grafos regulares.
Um grafo é $k$-regular se todos os seus nós têm grau $k$.
Dado um inteiro $k \geq 1$,
prove que todo grafo bipartido $k$-regular
tem um emparelhamento
perfeito.
Deduza daí que todo grafo bipartido $k$-regular
tem $k$ emparelhamentos perfeitos
disjuntos entre si.
[CCPS 3.23]
-
Mostre que as conclusões do exercício
Grafos regulares
são falsas se
grau $k$
for trocado por grau pelo menos $k$
.
[CCPS 3.24]
-
Cobertura por caminhos curtos.
Um conjunto $X$ de nós de um grafo é independente
se nenhuma aresta tem ambas as pontas em $X$.
Uma cobertura de um grafo por caminhos curtos
é uma coleção de caminhos de comprimento $\leq 1$
tal que todo nó do grafo está em pelo menos um dos caminhos da coleção.
Prove que num grafo bipartido
qualquer conjunto independente máximo tem o mesmo tamanho que
uma cobertura mínima por caminhos curtos.
(Dica: Use o teorema de Kőnig.)
-
Teorema de Menger dirigido.
Num grafo dirigido,
dois caminhos dirigidos
são internamente disjuntos
se os únicos nós que eles têm em comum são o primeiro e o último.
Dados nós $r$ e $s$ de um grafo dirigido $D$,
um subconjunto $S$ de $V(D)\setm \conj{r,s}$
isola $r$ de $s$
se não existe caminho dirigido de $r$ a $s$ em $D\setm S$.
Prove o seguinte teorema de
K. Menger
(1927):
o número máximo de caminhos dirigidos de $r$ a $s$
que são internamente disjuntos
é igual ao tamanho de um conjunto de nós que isola $r$ de $s$.
[CCPS 3.42]
-
Teorema de Menger não-dirigido.
Enuncie e prove um resultado análogo ao teorema de Menger
(veja o exercício
Teorema de Menger dirigido acima)
para grafos não-dirigidos.
[CCPS 3.43]