Este capítulo resolve o problema do emparelhamento perfeito em grafos não-dirigidos. A solução do problema — que começou com W. Tutte em 1947 e culminou com J. Edmonds em 1965 — é um importante marco no desenvolvimento da otimização combinatória (e do conceito de classe NP de problemas).
Todos os grafos neste capítulo serão não-dirigidos. Por isso, diremos simplesmente grafo, deixando subentendido o adjetivo não-dirigido. Muitos dos conceitos básico usados abaixo foram definidos no capítulo 6. Para as definições de outros termos técnicos, consulte o índice remissivo e os apêndices.
Um
emparelhamento
num grafo é perfeito
(= perfect matching)
se satura todos os nós do grafo,
ou seja, se não deixa nós expostos.
Para simplificar, adotaremos a abreviatura ep
para a expressão emparelhamento perfeito
.
Eis o problema central deste capítulo:
Problema 7.A (do ep) Encontrar um emparelhamento perfeito num grafo.
O capítulo anterior fez várias considerações preliminares importantes sobre o problema. Em particular, observou que muitas instâncias do problema não têm solução. Trataremos dessa questão a seguir.
Que condições são necessárias e suficientes para a existência de um ep? Como provar que um dado grafo não tem um ep?
Se um grafo $G$ tem um ep então é claro que $|V(G)|$ é par. Ademais, se $G$ tem um ep então toda cobertura de $G$ tem pelo menos $|V(G)|/2$ nós. Mas essas condições necessárias não são suficientes para garantir um ep.
Uma condição necessária mais forte envolve o conceito de componente ímpar. Uma componente ímpar (= odd component) de um grafo $G$ é qualquer componente conexa de $G$ que tenha um número ímpar de nós. O número de componentes ímpares de $G$ será denotado por $\oc(G)$.
Lema 7.2 (das componentes ímpares) Se um grafo $G$ tem um emparelhamento perfeito então $\oc(G{-}A) \leq |A|$ para todo subconjunto próprio $A$ de $V(G)$.
A expressão $G{-}A$ denota o subgrafo de $G$ induzido por $V(G)\setm A$. Essa notação será usada com frequência no que segue.
Prova do lema: Seja $A$ um conjunto de nós, $M$ um ep, e $k:=\oc(G{-}A)$. Sejam $H_1,\ldots,H_k$ as componentes ímpares de $G{-}A$.
Para cada $i$, seja $V_i:=V(H_i)$ e $M_i:= M\cap E(H_i)$. Como $|V_i|$ é ímpar, temos $2|M_i|\leq |V_i| - 1$. Como $M$ é perfeito, algum nó de $H_i$ está ligado a $A$ por uma aresta de $M$. Portanto, temos $k$ arestas com um ponta em $A$ e outra fora de $A$. Como $M$ é um emparelhamento, no máximo $|A|$ arestas de $M$ podem ter uma ponta em $A$. Portanto, $k \leq |A|$. ■
Embora isso esteja longe de ser óbvio, a condição necessária estabelecida no lema é também suficiente. É o que afirma o seguinte teorema de W. Tutte:
Teorema 7.3 (de Tutte) Para qualquer grafo $G$, se $\oc(G{-}A) \leq |A|$ para todo subconjunto próprio $A$ de $V(G)$ então $G$ tem um emparelhamento perfeito.
Essa condição para a existência de um ep é conhecida como condição de Tutte. Uma prova algorítmica do teorema será discutida mais adiante neste capítulo.
Componentes unitárias. As componentes conexas de $G{-}A$ que têm apenas um nó merecem atenção. Denotaremos por $\oc_1(G{-}A)$ o número de componentes unitárias de $G{-}A$, ou seja, o número de nós isolados de $G{-}A$. Segue trivialmente do lema 7.2 que todo grafo $G$ dotado de ep satisfaz a condição $\oc_1(G{-}A)\leq |A|$ para todo $A \subset V(G)$. O teorema de Kőnig — teorema 6.4 do capítulo anterior — mostra que essa condição também é suficiente quando $G$ é bipartido:
Corolário 7.4 (do teorema de Kőnig) Para qualquer grafo bipartido $G$, se $\oc_1(G{-}A) \leq |A|$ para todo subconjunto próprio $A$ de $V(G)$ então $G$ tem um emparelhamento perfeito.
A prova do corolário é simples: basta observar que $A$ é uma cobertura se e somente se todos os nós de $G-A$ são isolados.
Podemos tratar agora da solução algorítmica do problema 7.A. Gostaríamos de ter um algoritmo que receba um grafo e produza um de dois objetos: um ep ou um conjunto de nós que viole a condição de Tutte. O conjunto que viola a condição de Tutte serviria como evidência de que o grafo não tem ep.
Cada iteração do algoritmo começa com um emparelhamento imperfeito $M$ e procura um caminho aumentador; se encontrar um caminho aumentador $P$, troca $M$ por $M\symdiff E(P)$ e começa nova iteração; senão, encontra uma violação da condição de Tutte e para.
À primeira vista, para encontrar um caminho aumentador basta executar uma variante apropriada do algoritmo de busca em largura (veja a seção 1.8 do capítulo 1). Mas o processo é bem mais complexo pois o caminho que procuramos deve ser alternante.
Dado um emparelhamento imperfeito $M$ e
um nó $r$ exposto por $M$,
a busca por um caminho $M$-
Diremos que uma tal árvore é $M$-alternante
e que $r$ é a raiz da árvore.
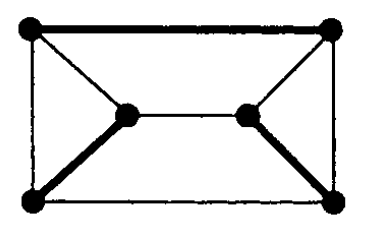
Exemplo 7.1:
A figura mostra uma árvore $M$-alternante com raiz $r$.
O resto do grafo não aparece na figura.
As linhas mais grossas representam as arestas de $M$.
Suponha que $T$ é uma árvore $M$-alternante
com raiz $r$.
Para qualquer nó $v$ de $T$,
a distância de $r$ a $v$
é o comprimento
do único caminho
de $r$ a $v$ em $T$.
Dizemos que um nó $v$ de $T$ é branco
se a distância de $r$ a $v$ é ímpar,
e preto se a distância de $r$ a $v$ é par.
Se $A$
é o conjunto dos nós brancos de $T$
e $B$ o conjunto dos nós pretos de $T$
então é claro que $|B| = |A| +1$.
Dizemos que a árvore $T$ é frustrada
se toda aresta de $G$ com uma ponta preta
tem a outra ponta branca.
(Em particular, de $T$ é frustrada então
nenhuma aresta de $G$ tem uma ponta preta
e a outra fora de $V(T)$.)
Árvores frustradas são incompatíveis com ep's:
Lema 7.5 (da árvore frustrada)
Se $G$ tem
uma árvore $M$-alternante frustrada então
$G$ não tem emparelhamento perfeito.
Prova:
Seja $T$ uma árvore $M$-alternante frustrada.
Seja $A$ o conjunto dos nós brancos de $T$
e $B$ o conjunto dos nós pretos.
Toda aresta de $G$ com uma ponta em $B$ tem a outra em $A$.
Portanto,
cada nó de $B$ é isolado
em $G{-}A$
e assim constitui uma componente ímpar de $G{-}A$.
Logo,
$\oc_1(G{-}A) \geq \text{}$ $|B| = \text{}$ $|A|+1$.
De acordo com o
lema 7.2,
a existência de um tal $A$ mostra que $G$ não tem ep algum. ■
Diremos que um nó $w$ de $V(G)\setm V(T)$ é
vermelho se estiver $M$-exposto
e verde em caso contrário.
Diremos que uma aresta $vw$ é preto-verde
se $v$ é preto e $w$ é verde.
Analogamente, $vw$ é preto-vermelha se $v$ é preto e $w$ é vermelho.
Exemplo 7.2:
Veja abaixo a matriz de adjacências de um grafo.
Use o gabarito de posição dos nós para fazer uma figura.
Tome o emparelhamento $M=\conj{ac,gd,fh}$.
Seja $T$ a árvore $M$-alternante com nós $a$, $b$, $c$, $d$ e $g$
e arcos $ba$, $ac$, $cg$ e $gd$.
Os nós $b$, $c$ e $d$ são pretos.
Os nós $a$ e $g$ são brancos.
Os nós $f$ e $h$ são verdes e o nó $e$ é vermelho.
Não há arestas preto-verdes nem preto-vermelhas.
A árvore $T$ é frustrada. Observe que $\oc_1(G{-}A) = 4 > 2 = |A|$,
sendo $A:=\conj{a,g}$ o conjunto de nós brancos.
Dada uma aresta preto-verde $vw$,
seja $wz$ a aresta de $M$ que incide em $w$.
(É claro que $z$ não está em $T$.)
Podemos acrescentar $vw$ e $wz$ a $T$
e assim estender a árvore.
Dada uma aresta preto-vermelha $vw$,
o caminho simples de $r$ a $w$
em $T+vw$
é $M$-aumentador e
pode ser usado para produzir um novo emparelhamento,
maior que $M$.
Encapsulamos essas operações em duas rotinas:
Suponha agora que nenhuma dessas operações pode ser executada.
Então todas as arestas de $G$ com uma ponta preta
têm a outra ponta branca ou preta.
Diremos que uma aresta de $G$ é
preto-branca se tem uma ponta preta e a outra branca
e é preto-preta se ambas as pontas são pretas.
Se não existem arestas preto-pretas então $T$ é frustrada.
Se existe uma aresta preto-preta, digamos $vw$,
então
$T+vw$ tem um circuito
de comprimento ímpar.
Não é fácil lidar com esses circuitos ímpares.
Trataremos disso na seção 7.5.
Na próxima seção, vamos nos ocupar de grafos que não têm circuito ímpar algum.
As ideias da seção anterior
são suficientes para resolver o problema 7.A
em grafos bipartidos
pois esses grafos não têm circuitos ímpares
(veja o
lema E.2).
O correspondente algoritmo recebe um grafo bipartido $G$ e devolve
um ep ou um conjunto $A$
de nós tal que
$\oc_1(G{-}A) > |A|$.
No início de cada execução do bloco de linhas 03–12,
$M$ é um emparelhamento imperfeito.
No início de cada execução do bloco de linhas 06–07,
$T$ é uma árvore $M$-alternante com raiz $r$.
Na linha 09,
o grafo não tem arestas preto-verdes nem preto-vermelhas.
Também não tem arestas preto-pretas,
uma vez que, para qualquer aresta $vw$ desse tipo,
o grafo $T+vw$ teria um circuito ímpar.
Portanto, a árvore $T$ é frustrada.
Assim, de acordo com o lema 7.5,
$G$ não tem ep.
(Esse algoritmo é essencialmente igual ao que foi descrito,
em termos de fluxo máximo,
na prova do teorema 6.3.)
Exemplo 7.3:
Aplique o algoritmo EmpBipartidoPerfeito
ao grafo $G$
representado pela matriz de adjacências abaixo.
Use o gabarito de posição dos nós para fazer uma figura.
Examine os nós em ordem alfabética.
A execução do algoritmo termina com $M:=\conj{ab,cd}$
e com a árvore $M$-alternante $T$ que tem raiz $e$
e arestas $ec$ e $cd$.
Os nós $e$ e $d$ são pretos,
o nó $c$ é branco,
os nós $a$ e $b$ verdes,
e todos os demais nós são vermelhos.
Não há arestas preto-verdes, nem preto-vermelhas, nem preto-pretas,
e a árvore $T$ é frustrada.
O algoritmo devolve o conjunto $A:=\conj{c}$,
que viola a condição de Tutte.
(Note que a execução do algoritmo termina antes de examinar o grafo todo.)
Retomemos a discussão que a seção anterior interrompeu.
Seja $M$ um emparelhamento imperfeito num grafo arbitrário $G$
e $T$ uma árvore $M$-alternante.
Suponha agora que alguma aresta $vw$ de $G$ é preto-preta.
Nesse caso, como já observamos acima, $T+vw$ tem um
circuito ímpar.
Diremos que esse circuito é uma flor
(= blossom).
O algoritmo
que passamos a descrever
contrai a flor
para revelar caminhos $M$-aumentadores
que não correspondem a arestas preto-vermelhas de $T$
(como acontece na
rotina AumentaEmp).
Contração de flores.
A contração
(= shrinking)
de uma flor $C$
é a operação que produz um novo grafo
que tem conjunto de nós $(V(G)\setm V(C))\cup \conj{C}$ e
conjunto de arestas
definido da seguinte maneira:
para cada aresta $vw$ tal que $v\notin V(C)$,
se $w\notin V(C)$
então $vw$ é aresta do novo grafo
e se $w \in V(C)$ então $vC$ é aresta do novo grafo.
(As eventuais
Exemplo 7.4:
A figura mostra uma flor
$C$ num grafo $G$
e o grafo $G{\times}C$ que resulta da contração de $C$.
A contração da flor $C$ preserva boa parte das estruturas
presentes em $G$:
as arestas de $M$ e $T$ que não têm ambas as pontas em $C$
constituem um
emparelhamento $M'$
e uma árvore $T'$
em $G{\times}C$.
A árvore $T'$ é $M'$-alternante.
Do ponto de vista de $T'$,
o nó
que resulta da contração de $C$ é preto
(pois o caminho em $T'$ que vai da raiz até o nó tem comprimento par),
todo nó branco de $G-C$ continua branco,
e todo nó preto de $G-C$ continua preto.
Podemos
encapsular a operação de contração de uma flor em uma rotina:
Depois da execução dessa rotina,
$M$ é um emparelhamento em $G$,
$T$ é uma árvore $M$-alternante de $G$ e $C$ é um nó preto.
Exemplo 7.5:
A primeira das figuras abaixo mostra uma árvore
$M$-alternante $T$.
As linhas tracejadas representam arestas que
não pertencem a $T$.
Uma dessas arestas liga um nó branco
a um nó vermelho $u$.
Há um caminho aumentador que começa em $r$,
O circuito ímpar $C$ em $T+vw$ é uma flor.
A segunda figura representa o grafo $G{\times}C$.
Na nova árvore alternante, $C$ é um nó preto,
a aresta $Cu$ é preto-vermelha,
e o caminho aumentador de $r$ a $u$ ficou visível.
Grafo derivado e pseudonós.
Uma
sequência de contrações de flores transforma o grafo $G$
em um grafo derivado $G'$.
O grafo derivado tem dois tipos de nós:
os nós originais e os pseudonós.
Um pseudonó de $G'$ é o resultado da contração de uma flor,
enquanto um nó original de $G'$ é um nó de $G$.
Os pseudonós são recursivos:
uma flor pode conter pseudonós produzidos por contrações anteriores.
Para cada nó $v$ do grafo derivado $G'$,
denotamos por $S(v)$ o conjunto de nós de $G$
Suponha que $M'$ é um emparelhamento em um grafo derivado $G'$
e $T'$ é uma árvore $M'$- Lema 7.6 (da árvore frustrada)
Se a árvore $T'$ é frustrada
então o grafo original $G$ não tem
emparelhamento perfeito.
Prova:
Seja $A$ o conjunto dos nós brancos de $T'$
(esses nós estão à distância ímpar da raiz em $T'$)
e $B$ o conjunto dos nós pretos
(esses nós estão à distância par da raiz em $T'$).
Como $T'$ é frustrada,
toda aresta de $G'$ com uma ponta
em $B$ têm a outra ponta
em $A$.
Portanto, cada nó de $B$ constitui uma componente ímpar de $G'{-}A$.
Como todos os nós de $A$ são originais,
faz sentido examinar o grafo $G{-}A$.
O conjunto de nós de cada componente ímpar de $G{-}A$
é igual a $S(v)$ para algum $v$ em $B$.
Logo, $\oc(G{-}A) \geq |B|$.
Como $|B| = |A|+1$,
o conjunto $A$ viola a condição de Tutte
(veja o lema 7.2).
Portanto $G$ não tem um ep. ■
Expansão.
Suponha agora que encontramos um caminho $M'$-aumentador
no grafo derivado $G'$.
Esse caminho aumentador é usado para calcular um novo emparelhamento
em $G'$.
Feito isso, os pseudonós são descontraídos e o novo emparelhamento
é expandido
Se $C$ é uma flor em $G$,
qualquer emparelhamento $M'$ no grafo contraído $G{\times}C$ pode ser
expandido
de modo a produzir um emparelhamento
$M$, subconjunto de $M'\cup E(C)$,
em $G$.
Essa expansão consiste em acrescentar $\frac{1}{2}(|V(C)|-1)$ arestas de $C$
a $M'$.
Com isso,
o número de nós que $M$ deixa expostos em $G$
é igual ao
número de nós que $M'$ deixava expostos em $G{\times}C$.
Exemplo 7.6:
A figura mostra a flor $C$ e o grafo $G{\times}C$ do
exemplo 7.4.
Em seguida,
mostra um emparelhamento (arestas escuras) no grafo $G{\times}C$
e a expansão
desse emparelhamento para dentro de $C$,
produzindo um emparelhamento em $G$.
A operação de descontração de flores é aplicada, recursivamente,
a todos os pseudonós do grafo derivado $G'$.
Isso produz um novo emparelhamento no grafo original $G$.
Esse novo emparelhamento deixa menos nós expostos que o emparelhamento original.
Vamos encapsular a operação na seguinte
O algoritmo que descrevemos na seção anterior foi publicado por
J. Edmonds
em 1965
e ficou conhecido como algoritmo das flores
(= blossom algorithm),
ou algoritmo de Edmonds para emparelhamento perfeito.
O algoritmo resolve o problema 7.A
em grafos arbitrários:
No início de cada iteração do bloco de linhas 03–16,
$M$ é um emparelhamento no grafo original $G$.
O objetivo desse bloco é encontrar um caminho $M$-aumentador
e assim substituir $M$ por um emparelhamento maior.
Esse objetivo é atingido linha 16.
No início de cada iteração do bloco de linhas 07–10,
temos um emparelhamento $M'$ num grafo derivado $G'$
e uma árvore $M'$-alternante $T'$.
Não há pseudonós brancos, ou seja,
todos os nós brancos são originais.
No linha 12, toda aresta de $G'$ com uma ponta preta
tem a outra ponta branca e portanto a árvore $T'$ é
frustrada.
De acordo com a prova do
o lema 7.6,
o conjunto $A'$ viola a condição de Tutte.
Exemplo 7.7:
Aplique o algoritmo EmpPerfeito
ao grafo $G$ definido pela matriz de adjacências abaixo.
O emparelhamento inicial $M:=\conj{\bo{bd},\bo{ce},\bo{fh},\bo{gi}}$
é indicado em magenta na matriz.
A primeira iteração produz a
árvore $M$-alternante $T$ com conjunto de arestas
\[
ab, \bo{bd}, ac, \bo{ce}, df, \bo{fh}, dg, \bo{gi}\text{.}
\]
O conjunto de nós pretos é $B:=\conj{\bl{a}, \bl{d}, \bl{e}, \bl{h}, \bl{i}}$
e o conjunto de nós brancos é $A:=\conj{b, c, f, g}$.
A raiz de $T$ é $\bl{a}$.
Não há nós verdes nem vermelhos pois $T$ cobre o grafo todo.
Suponha que o algoritmo escolhe a aresta $dh$,
que liga dois nós pretos
e assim forma a flor $K:=(\bl{d},\bl{h},f,\bl{d})$.
A contração da flor
transforma $G$ no grafo $G':=G{\times}K$
representado pela matriz à esquerda:
A contração também transforma $M$ no
emparelhamento $M'$,
indicado em magenta na matriz,
e transforma $T$ na árvore $M'$-alternante $T'$
cujas arestas são
\[
ab, \bo{bK}, ac, \bo{ce}, Kg, \bo{gi}\text{.}
\]
O conjunto de nós pretos é $B':=\conj{\bl{a}, \bl{e}, \bl{K}, \bl{i}}$
e o conjunto de nós brancos é $A':=\conj{b, c, g}$.
Em seguida, o algoritmo escolhe a aresta $Ki$,
que liga dois nós pretos e assim forma a flor $L:=(\bl{K},g,\bl{i},\bl{K})$.
A contração da flor
transforma $G'$ em $G'':=G{\times}L$
(veja a matriz de adjacências acima à direita),
transforma $M'$ em $M''$,
e trnsforma $T'$ na árvore $M''$-alternante $T''$
definida pelas arestas
\[
ab, \bo{bL}, ac, \bo{ce}\text{.}
\]
O conjunto de nós pretos é $B'':=\conj{\bl{a},\bl{e},\bl{L}}$ e
o conjunto de nós brancos é $A'':=\conj{b,c}$.
Todas as arestas que têm uma ponta preta têm a outra ponta branca.
Portanto, $T''$ é frustrada e
$A''$ viola as condições de Tutte em $G''$.
O conjunto $A''$ também viola as condições de Tutte no grafo original $G$.
Com efeito,
$\oc(G{-}A'') = \text{}$ $3 > \text{}$ $2 = \text{}$ $|A''|$.
As três componentes ímpares de $G{-}A''$ têm conjuntos de nós
$\conj{a}$,
$\conj{e}$ e $\conj{d,h,f,i,g}$.
Veja o rastreamento da execução do algoritmo
a partir do emparelhamento inicial $\conj{bd, ce, fh, gi}$:
Desempenho.
O desempenho do algoritmo
EmpPerfeito
pode ser inferido do número de execuções das rotinas auxiliares
AumentaEmp
(linha 15),
EstendeÁrvore (linha 09),
ContraiFlor
(linha 10) e
Expande
(linha 16).
Considere os eventos entre duas invocações consecutivas de
AumentaEmp.
Cada invocação de ContraiFlor
diminui $|V(G')|$ mas não altera $|V(G')\setm V(T)|$.
Cada invocação de EstendeÁrvore
diminui $|V(G')\setm V(T)|$ mas não altera $|V(G')|$.
Portanto,
temos no máximo $n:=|V(G)|$ invocações
de ContraiFlor
e de EstendeÁrvore
entre duas invocações consecutivas de AumentaEmp.
Como há um total de $\Oh(n)$ invocações de
AumentaEmp,
temos
$\Oh(n^2)$ invocações
de ContraiFlor
e $\Oh(n^2)$ invocações
de EstendeÁrvore.
O número de invocações de Expande
é $\Oh(n)$.
Estruturas de dados apropriadas
permitem implementar o algoritmo EmpPerfeito
de modo que o consumo total de tempo seja
$\Oh(mn \log n)$,
onde $m$ é o número de arestas e $n$ o número de nós do grafo.
Existe um algoritmo polinomial
para decidir se um grafo $G$
tem um emparelhamento perfeito.
O algoritmo produz um emparelhamento perfeito
ou prova que $G$ não tem emparelhamento perfeito.
A prova consiste em subconjunto próprio $A$ de $V(G)$ tal que
$\oc(G{-}A) > |A|$.
\[
\begin{array}[t]{l@{\quad}*{8}{c}}
& a & b & c & d & e & f & g & h \\[0.5ex]
a & - & 1 & 1 & 1 & 1 & 1 & - & - \\
b & 1 & - & - & - & - & - & 1 & - \\
c & 1 & - & - & - & - & - & 1 & - \\
d & 1 & - & - & - & - & - & 1 & - \\
e & 1 & - & - & - & - & - & - & - \\
f & 1 & - & - & - & - & - & - & 1 \\
g & - & 1 & 1 & 1 & - & - & - & - \\
h & - & - & - & - & - & 1 & - & -
\end{array}
\qquad\qquad
\begin{array}[t]{*{5}{c@{\hspace{4ex}}}}
& & & & \\[1.0ex]
& & a \hf & & \\[4ex]
b \hf & c \hf & d \hf & e \hf & f \\[4ex]
& g \hf & & & h
\end{array}
\]
Exercícios 7.3
7.4 O caso dos grafos bipartidos
EmpBipartidoPerfeito $(G)$
$\rhd$ $G$ é bipartido
01
.
seja $M$ um emparelhamento
$\rhd$ talvez $M \larr \emptyset$
02
.
enquanto emparelhamento $M$ não é perfeito faça
03
.ooo
seja $r$ um nó $M$-exposto
04
.ooo
$T \larr (\conj{r},\emptyset)$
05
.ooo
enquanto existe aresta preto-verde faça
06
.oooooo
seja $vw$ uma aresta preto-verde
07
.oooooo
$T \larr \text{}$ EstendeÁrvore $(G,M,T,vw)$
08
.ooo
se não existe aresta preto-vermelha
09
.oooooo
então seja $A$ o conjunto dos nós brancos de $T$
10
.oooooo
então devolva $A$ e pare
$\rhd$ $G$ não tem ep
11
.ooo
seja $vw$ uma aresta preto-vermelha
12
.ooo
$M \larr \text{}$ AumentaEmp $(G,M,T,vw)$
13
.
devolva $M$ e pare
$\rhd$ $M$ é perfeito
\[
\begin{array}[t]{l@{\quad}*{9}{c}}
& a & b & c & d & e & f & g & h & i \\[0.5ex]
a & - & 1 & - & - & - & - & - & - & - \\
b & 1 & - & - & - & - & - & - & - & - \\
c & - & - & - & 1 & 1 & 1 & - & - & - \\
d & - & - & 1 & - & - & - & - & - & - \\
e & - & - & 1 & - & - & - & - & - & - \\
f & - & - & 1 & - & - & - & 1 & - & - \\
g & - & - & - & - & - & 1 & - & 1 & - \\
h & - & - & - & - & - & - & 1 & - & 1 \\
i & - & - & - & - & - & - & - & 1 & -
\end{array}
\qquad\qquad
\begin{array}[t]{*{6}{c@{\hspace{4ex}}}}
& & & & & \\[1.0ex]
a \hf & & c \hf & & g \hf & i \\[6ex]
b \hf & d \hf & e \hf & f \hf & h \hf &
\end{array}
\]
Exercícios 7.4
\[
\begin{array}[t]{l@{\quad}cccccc}
& g & h & i & j & k & l \\[0.5ex]
a & 1 & - & - & - & - & - \\
b & - & 1 & - & - & - & - \\
c & - & 1 & 1 & - & - & - \\
d & - & - & - & 1 & - & - \\
e & - & - & - & 1 & - & - \\
f & - & - & - & - & 1 & -
\end{array}
\qquad\qquad
\begin{array}[t]{*{1}{c@{\hspace{3ex}}}*{2}{c@{\hspace{4ex}}}*{4}{c@{\hspace{3ex}}}}
& & & & & \\[1.0ex]
a \he & b \he & c \he & d \he & e \he & f \he & \\[6ex]
g \he & h \he & i \he & j \he & & k \he & l \\
\end{array}
\]
\[
\begin{array}[t]{l@{\quad}cccccc}
& e & f & g \\[0.5ex]
a & 1 & - & 1 \\
b & - & 1 & 1 \\
c & 1 & 1 & 1 \\
d & - & - & 1
\end{array}
\qquad\qquad
\begin{array}[t]{*{4}{c@{\hspace{4ex}}}}
& & & \\[0.5ex]
a \he & b \he & c \he & d \\[4ex]
e \he & f \he & & g \\
\end{array}
\]
7.5 Flores e contrações
diagonais
de $C$ não estão representadas no novo grafo.)
Esse novo grafo será denotado por $G{\times}C$.
desce
pela árvore até $w$,
percorre $wv$,
volta
pela árvore até o vizinho de $u$,
e finalmente chega a $u$.
Mas a rotina
AumentaEmp
não vê esse caminho aumentador
pois sua última aresta não é preto-vermelha.
contidos
em $v$.
A definição precisa de $S(v)$ é recursiva:
se $v$ é um nó original então $S(v) := \conj{v}$,
e se $v$ é o resultado da contração de uma flor $C$ então
$S(v) := \bigcup\,\conj{S(w) : w\in V(C)}$.
É claro que todo conjunto $S(v)$ tem cardinalidade ímpar
e $|S(v)|=1$ se e somente se $v$ é um nó original.
Além disso, a coleção $\conj{S(v) : v\in V(G')}$
é uma partição de $V(G)$.
para dentro
das flores.
Exercícios 7.5
primeiro
nó de $C$
tem comprimento par.
7.6 Algoritmo das flores para emparelhamento perfeito
EmpPerfeito $(G)$
$\rhd$ Blossom algorithm
01
.
seja $M$ um emparelhamento
$\rhd$ talvez $M \larr \emptyset$
02
.
enquanto o emparelhamento $M$ não é perfeito faça
03
.ooo
$G' \larr G$, $M' \larr M$
04
.ooo
seja $r$ um nó $M'$-exposto de $G'$
05
.ooo
$T' \larr (\conj{r},\emptyset)$
06
.ooo
enquanto $G'$ tem aresta preto-verde ou preto-preta
07
.oooooo
seja $vw$ uma aresta preto-verde ou preto-preta
08
.oooooo
se $vw$ é preto-verde
09
.ooooooooo
então $T' \larr \text{}$ EstendeÁrvore $(G',M',T',vw)$
10
.ooooooooo
senão ContraiFlor $(G',M',T',vw)$
11
.ooo
se $G'$ não tem aresta preto-vermelha
12
.oooooo
então seja $A'$ o conjunto dos nós brancos de $T'$
13
.oooooo
então devolva $A'$ e pare $\rhd$ $G$ não tem ep
14
.ooo
seja $vw$ uma aresta preto-vermelha
15
.ooo
$M' \larr \text{}$ AumentaEmp $(G',M',T',vw)$
16
.ooo
$M \larr \text{}$ Expande $(G',M')$
$\rhd$ descontrai todas flores
17
.
devolva $M$ e pare $\rhd$ $M$ é um ep
\[
\begin{array}[t]{l@{\quad}ccccccccc}
& a & b & c & d & e & f & g & h & i \\[0.5ex]
a & - & 1 & 1 & - & - & - & - & - & - \\
b & 1 & - & - &\bo{1}& 1 & - & - & - & - \\
c & 1 & - & - & - &\bo{1}& - & - & 1 & - \\
d & - &\bo{1}& - & - & - & 1 & 1 & 1 & - \\
e & - & 1 &\bo{1}& - & - & - & - & - & - \\
f & - & - & - & 1 & - & - & - &\bo{1}& - \\
g & - & - & - & 1 & - & - & - & - &\bo{1}\\
h & - & - & 1 & 1 & - &\bo{1}& - & - & 1 \\
i & - & - & - & - & - & - &\bo{1}& 1 & -
\end{array}
\qquad\qquad
\]
\[
\begin{array}[b]{l@{\quad}ccccccccc}
& a & b & c & e & K & g & i \\[0.5ex]
a & - & 1 & 1 & - & - & - & - \\
b & 1 & - & - & 1 &\bo{1}& - & - \\
c & 1 & - & - &\bo{1}& 1 & - & - \\
e & - & 1 &\bo{1}& - & - & - & - \\
K & - &\bo{1}& 1 & - & - & 1 & 1 \\
g & - & - & - & - & 1 & - &\bo{1}\\
i & - & - & - & - & 1 &\bo{1}& -
\end{array}
\qquad\qquad
\begin{array}[b]{l@{\quad}ccccccccc}
& a & b & c & e & L \\[0.5ex]
a & - & 1 & 1 & - & - \\
b & 1 & - & - & 1 &\bo{1} \\
c & 1 & - & - &\bo{1}& 1 \\
e & - & 1 &\bo{1}& - & - \\
L & - &\bo{1}& 1 & - & -
\end{array}
\]
\[
\begin{array}{ll}
\text{árvore} & \text{flor}\\
\hline\rule{0ex}{2.5ex}%
abd \ ace \ dfh & K := (d\ h\ f\ d)\\
abK \ ace \ Kgi & L := (K\ g\ i\ K)\\
abL \ ace
\end{array}
\]
Exercícios 7.6
7.7 Resumo e conclusões