Capítulo 4
Fluxo de custo mínimo
Este capítulo generaliza o problema de Gale
(seção 3.1)
e procura um fluxo que satisfaça demandas dos nós,
respeita as capacidades dos arcos,
e faça tudo isso ao menor custo possível.
Para resolver o problema, o capítulo
usa as ferramentas desenvolvidas
na seção 3.1,
no capítulo 1
(caminhos dirigidos de custo mínimo),
e no capítulo 2
(fluxos de intensidade máxima).
Os ingredientes do problema são os mesmos dos capítulos anteriores:
um grafo dirigido
$D:=(V,E)$,
uma função-demanda
$(b_v : v\in V)$
com valores em $\R$,
uma função-capacidade
$(u_e : e\in E)$
com valores
em $\Rplus$,
e uma função-custo
$(c_e : e\in E)$
com valores em $\R$.
[Poderíamos escrever
$b\in \R^{V}$
,
$u\in \Rplus^{E}$
e $c \in \R^{E}$
.
Seria mais realista trocar todos os $\R$
por $\Q$
,
uma vez que computadores digitais
não conhecem números irracionais.]
Note que $u\geq 0$
mas $b$ e $c$
não têm restrição de sinal.
(Consulte o
índice remissivo
e os apêndices
para conferir as definições de termos técnicos.)
4.1 O problema
Um fluxo numa rede $(D,b,u)$
é qualquer vetor $(x_e : e\in E)$
com valores em $\Rplus$.
Um fluxo $x$ respeita $u$
se $x \leq u$ e
satisfaz $b$ se
\[
\xinout \ = \ b\,\text{.}
\]
(Como na seção 2.1,
para cada nó $v$,
$\xinout(v)$ é a quantidade de fluxo que entra em $v$
menos a quantidade de fluxo que sai de $v$.)
Um fluxo $x$ é viável
se satisfaz $b$ e respeita $u$.
Dada uma função-custo $c$,
o custo
de um fluxo $x$ é o número $cx$.
Convém lembrar que $c$ não tem restrições de sinal:
podemos ter $c_e \lt 0$ em alguns arcos e $c_e \geq 0$ em outros.
Problema 4.A (fluxo de custo mínimo)
Encontrar um fluxo viável
de custo mínimo numa rede $(D,b,u,c)$.
(Poderíamos dizer que esse é o
problema de Gale
com custos.)
Em inglês, o problema é conhecido como minimum-cost flow problem.
Muitas vezes, dizemos simplesmente fluxo de custo mínimo
,
deixando o viável
subentendido.
Dizemos também que um fluxo é ótimo
se for viável e tiver custo mínimo.
Uma rede de fluxo com custos
é qualquer rede $(D,b,u,c)$ que tenha os parâmetros
$b$, $u$, $c$
que acabamos de descrever.
Uma tal rede é viável
se tem um fluxo viável.
De acordo com o
lema 3.1
e o teorema de Gale
(teorema 3.2),
a rede é viável se e somente se
\[
b(V)=0 \hspace{2.5ex} \text{e} \hspace{2.5ex} b(X)\leq \uin(X)
\]
para todo subconjunto $X$ de $V$.
(Essas condições também podem ser escritas
de maneira mais simétrica:
$-\uout(X) \leq \text{}$ $b(X) \leq \text{}$ $\uin(X)$
para todo $X\subseteq V$.)
Toda rede viável tem um fluxo de custo mínimo
pois todo fluxo viável é limitado:
$x_e \leq u(E)$
para todo fluxo viável $x$
e todo arco $e$.
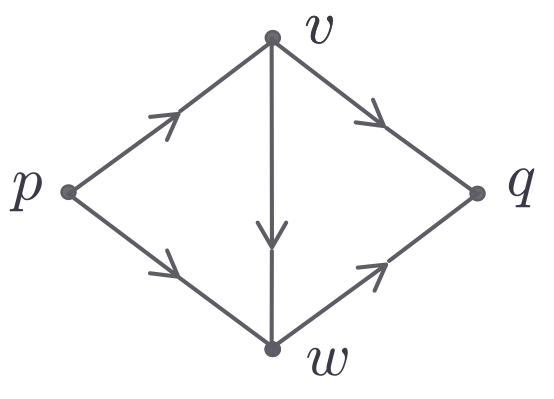
Exemplo 4.1:
Seja $D$ o grafo dirigido
com nós $p \ v \ w \ q$ descrito abaixo
por sua matriz de adjacências.
A função-demanda $b$ está representada à direita da matriz.
Mais à direita,
as capacidades e os custos dos arcos
bem como dois diferentes fluxos viáveis, $x$ e $x'$.
Verifique que
$cx =
240$ e
$cx' =
180$.
Observe como é fácil conferir a viabilidade e o custo de um fluxo
percorrendo as linhas da tabela.
\[
\begin{array}[t]{*{5}{r}@{\qquad}r}
& p & v & w & q & \hf b \\[0.5ex]
p & - & 1 & 1 & - & \hf -2 \\
v & - & - & 1 & 1 & \hf -1 \\
w & - & - & - & 1 & \hf +1 \\
q & - & - & - & - & \hf +2
\end{array}
\hspace{5ex}
\begin{array}[t]{l*{5}{r}}
& pv & pw & vw & vq & wq \\[0.5ex]
\hline
u & 3 & 3 & 3 & 3 & 3 \\
x & 0 & 2 & 0 & 1 & 1 \\
x'& 0 & 2 & 1 & 0 & 2 \\
c & \hb-30 & \hb +80 & \hb +40 & \hb +90 & \hb -10
\end{array}
\]
Exercícios 4.1
-
Suponha que $a$ é um arco de custo máximo na rede, ou seja,
$c_a := \max\,(c_e : e\in E)$.
Se $x$ é um fluxo viável de custo mínimo, é verdade que $x_a = 0$?
-
O problema do caminho dirigido de custo mínimo
(problema 1.A
no capítulo 1)
é um caso particular do problema fluxo de custo mínimo
(problema 4.A)?
-
Mostre que o problema do fluxo de intensidade máxima
de um nó $r$ a um nó $s$
numa rede capacitada
(problema 2.A no capítulo 2)
é um caso particular do problema 4.A.
(Dica: acrescente arco $sr$ ao grafo.)
[CCPS 4.7]
-
★
Seja $(D,b,u,c)$ uma rede viável.
Mostre
que a rede não é ilimitada,
ou seja, tem um fluxo ótimo.
-
Um
emparelhamento
num grafo não-dirigido é perfeito
se incide em todos os nós.
Considere o problema de encontrar um emparelhamento perfeito
de custo mínimo em um grafo não-dirigido bipartido.
Formule esse problema como um caso particular
do problema 4.A.
[CCPS 4.2]
-
Seja $D$ um grafo dirigido
tal que o número $|\cutin(v)|+|\cutout(v)|$ é par em cada nó $v$.
Para cada arco $vw$,
seja $c_{vw}$ o custo de inverter $vw$
(isto é, trocar $vw$ por $wv$).
Queremos encontrar um conjunto de arcos
de custo mínimo
cuja inversão faz com que $D$ tenha um
ciclo dirigido
euleriano
(veja exercício na seção 3.1).
Formule esse problema como um caso particular
do problema 4.A.
[CCPS 4.5]
-
Atribuição de terminais a concentradores.
Uma rede de teleprocessamento tem um grande número de terminais
geograficamente dispersos e uma CPU.
É dado um conjunto de concentradores, instalados em certos lugares,
sendo cada um ligado à CPU por uma linha de alta capacidade e custo nulo.
Cada terminal precisa ser ligado à CPU e
a ligação pode ser direta ou pode passar por um concentrador.
Cada concentrador pode cuidar de até $k$ terminais.
Para cada terminal $j$, o custo de uma ligação direta com a CPU é $d_{j}$
e o custo de uma ligação com um concentrador $i$ é $d_{ij}$.
Queremos determinar a maneira mais barata de ligar os terminais à CPU.
Formule esse problema como um caso particular
do problema 4.A.
[AMO 9.7]
-
★
Roteamento de cargueiros vazios.
Para um certo conjunto $V$ de portos marítimos,
temos os seguinte dados
relativos ao ano que passou:
para cada porto $v$, temos
o número $p_v$ de toneladas de carga que entraram no porto e
o número $q_v$ de toneladas de carga que saíram do porto.
Em cada porto $v$,
a diferença $b_v := p_v-q_v$ é uma medida do suprimento de cargueiros vazios
em $v$
e $-b_v$ é uma medida da demanda por cargueiros vazios
em $v$.
Cada cargueiro vazio saiu de um porto $v$ em que $b_v$ é positivo
e foi para um porto $w$ em que $b_w$ é negativo.
Se a distância do porto $v$ ao porto $w$ é de $c_{vw}$ milhas,
o deslocamento de $v$ a $w$
de um cargueiro vazio com capacidade para $t$ toneladas
representa um desperdício de $tc_{vw}$ toneladas$\times$milha.
Queremos organizar a movimentação de cargueiros vazios
de modo a minimizar o desperdício total anual.
[Sch17 p.73]
4.2 Programação linear
Na linguagem da programação linear,
o problema do fluxo de custo mínimo
(problema 4.A)
pode ser formulado assim:
encontrar um vetor real $(x_v : v\in V)$ que
\begin{equation}\label{lp:min-cost-flow}
\begin{array}{rcl@{\quad}l}
\text{minimize} \hspace{2ex} cx & \\[0.4ex]
\text{sujeito a} \hspace{2ex}
\xinout(v) & \hb = & \hb b_v & \text{para cada $v\in V$}\\
x_{e} & \hb \leq & \hb u_{e} & \text{para cada $e\in E$}\\
x_{e} & \hb \geq & \hb 0 & \text{para cada $e\in E$.}
\end{array}
\end{equation}
(Convém lembrar que podemos ter
$c_e \geq 0$ em alguns arcos e $c_e \lt 0$ em outros.)
Esse programa linear pode ser escrito assim em termos da
matriz de incidências
$A$ do grafo $D$:
\[
\begin{split}
\text{minimize} \hspace{2ex} cx & \\
\text{sujeito a} \hspace{2ex} Ax & \ = \ b \\
x & \ \leq \ u \\
x & \ \geq \ 0\,\text{.}
\end{split}
\]
O dual desse pl
consiste em encontrar vetores reais
$(y_v : v \in V)$ e $(z_e : e \in E)$ que
\[
\begin{split}
\text{maximizem} \hspace{2ex} yb + zu & \\
\text{sujeito a} \hspace{2ex} yA + z & \ \leq \ c \\
z & \ \leq \ 0
\end{split}
\]
e esse dual pode ser escrito por extenso assim:
encontrar $y$ e $z$ que
\begin{equation}\label{lp:min-cost-flow-dual}
\begin{array}{rcl@{\quad}l}
\text{maximizem} \hspace{2ex} yb + zu & \\
\text{sujeito a} \hspace{2ex}
y_w - y_v + z_{vw} & \hb \leq & \hb c_{vw} & \hb \text{para $vw\in E$}\\
z_{vw} & \hb \leq & \hb 0 & \hb \text{para $vw\in E$.}
\end{array}
\end{equation}
Para qualquer solução viável $x$
do pl \eqref{lp:min-cost-flow}
e qualquer solução viável $(y,z)$ do pl \eqref{lp:min-cost-flow-dual}
temos então
\begin{equation}\label{eq:weak-duality-proof}
\begin{split}
cx & \ \geq \ (yA + z) x \\
& \ = \ (yA)x + zx \\
& \ = \ y(Ax)+zx \\
& \ \geq \ yb + zu\,\text{.}
\end{split}
\end{equation}
Se $cx = yb + zu$ então $x$ é solução ótima
de \eqref{lp:min-cost-flow}
e $(y,z)$ é solução ótima
de \eqref{lp:min-cost-flow-dual}.
O teorema forte da dualidade
garante a recíproca:
se os dois pl's
são viáveis então
existe $x$ viável no primal
e existe $(y,z)$ viável no dual
tais que $cx=yb+zu$.
Essa igualdade equivale às
condições de folgas complementares:
Lema 4.1 (folgas complementares)
Para qualquer solução viável $x$ do pl \eqref{lp:min-cost-flow}
e qualquer solução viável $(y,z)$ do pl \eqref{lp:min-cost-flow-dual},
a igualdade $cx = yb+zu$ vale se e somente se
-
$x_{vw}=0$ ou
$y_w - y_v + z_{vw} = c_{vw}$ e
-
$x_{vw}=u_{vw}$ ou $z_{vw} = 0$
para cada arco $vw$.
Prova:
Temos $cx=yb+zu$ em \eqref{eq:weak-duality-proof}
se e somente se
$cx=(yA + z)x$ e $y(Ax)+zx = yb+zu$.
A primeira igualdade vale se e somente se
$x_e=0$ ou $(yA)_e + z_e = c_e$ para cada arco $e$.
(O ou
não é exclusivo.)
A segunda igualdade vale se e somente se $zx=zu$,
e esta última vale se e somente se $z_e=0$ ou $x_e=u_e$
para cada arco $e$. ■
As condições 1 e 2 de folgas complementares
podem também ser formuladas assim:
para cada arco $vw$,
-
se $x_{vw} > 0$ então
$y_w - y_v + z_{vw} = c_{vw}$ e
-
se $x_{vw} \lt u_{vw}$ então $z_{vw} = 0$.
Segue daí imediatamente que
se $0 \lt x_{vw} \lt u_{vw}$ então
$y_w - y_v = c_{vw}$.
Algoritmo.
Poderíamos resolver o
problema 4.A
submetendo o programa linear \eqref{lp:min-cost-flow}
ao algoritmo Simplex.
Mas isso é ineficiente,
uma vez que o Simplex,
que foi projetado para programas lineares arbitrários,
não leva em conta as muitas peculiaridades do
pl \eqref{lp:min-cost-flow}.
Exercícios 4.2
-
Verifique que o pl \eqref{lp:min-cost-flow-dual}
é dual do pl \eqref{lp:min-cost-flow}.
-
★
Mostre que o pl dual \eqref{lp:min-cost-flow-dual}
é viável,
ou seja, exiba alguma solução viável $(y,z)$ do pl.
-
Suponha que $b(V)\neq 0$ numa rede $(D,b,u,c)$ de fluxo com custos.
Mostre que o pl \eqref{lp:min-cost-flow}
é inviável nesse caso.
Mostre que o pl
dual \eqref{lp:min-cost-flow-dual}
é
ilimitado nesse caso
(ou seja, $yb+zu$ não tem máximo).
-
Suponha que $b(X) > \uin(X)$ para algum $X\subseteq V$.
Mostre que pl \eqref{lp:min-cost-flow} é inviável nesse caso.
Mostre que o pl dual \eqref{lp:min-cost-flow-dual}
é
ilimitado nesse caso
(isto é, $yb+zu$ não tem máximo).
-
A leitura descuidada das condições no enunciado
do lema 4.1
pode levar a interpretações erradas.
Qual a diferença entre as duas afirmações a seguir?
Afirmação A:
para cada $vw$ temos $x_{vw} = 0$ ou $y_w-y_v + z_{vw} = c_{vw}$.
Afirmação B:
temos $x_{vw} = 0$ para cada $vw$ ou
temos $y_w-y_v + z_{vw} = c_{vw}$ para cada $vw$.
-
Enuncie o problema do fluxo viável de custo máximo.
Escreva o pl do problema.
Escreva o pl dual.
Como poderíamos usar um algoritmo para o problema 4.A
para resolver o problema do fluxo viável de custo máximo?
4.3 Condições de otimalidade
Obtida uma solução $x$ do problema do fluxo de custo mínimo
(problema 4.A),
que informação
é possível apresentar para certificar a minimalidade
de $cx$?
Como o problema 4.A é idêntico ao
programa linear \eqref{lp:min-cost-flow},
qualquer solução viável $(y,z)$
do pl dual \eqref{lp:min-cost-flow-dual}
que satisfaça a igualdade $yb+zu = cx$ é um excelente certificado.
Alternativamente,
podemos exibir uma solução viável $(y,z)$
que satisfaz as condições de folgas complementares
do lema 4.1.
Melhor ainda:
podemos omitir $z$ e exibir apenas um vetor $y$ apropriado,
como mostra o seguinte teorema.
Para enunciar o teorema, convém usar a palavra potencial
para designar qualquer vetor
$(y_v : v\in V)$ com valores em $\R$.
Teorema 4.2 (condições de otimalidade)
Um fluxo viável $x$ numa rede $(D,b,u,c)$ é ótimo
se e somente se
existe um potencial $y$
que satisfaz duas condições em cada arco $vw$:
-
$x_{vw}=0$ ou
$y_w - y_v \geq c_{vw}$ e
-
$x_{vw}=u_{vw}$ ou $y_w - y_v \leq c_{vw}\,$.
Prova:
Para provar a parte se
, suponha que $y$ é um potencial
que satisfaz as condições 1 e 2.
Seja $z$ o vetor definido por
\begin{equation}\label{eq:definition-of-z}
z_{vw} := \min\left(0,\,c_{vw} - y_w + y_v\right)
\end{equation}
para cada arco $vw$.
Em outras palavras, se $y_w-y_v \leq c_{vw}$ então $z_{vw}:=0$,
senão
$z_{vw} := \text{}$
$c_{vw} - y_w + y_v$.
Observe que o par $(y,z)$ é solução viável
do pl \eqref{lp:min-cost-flow-dual}.
Além disso, para cada arco $vw$, temos
$x_{vw} = 0$ ou $y_w{-}y_v{+}z_{vw} = c_{vw}$
bem como
$x_{vw} = u_{vw}$ ou $z_{vw} = 0$.
O lema 4.1
garante agora que $cx=yb+zu$ e portanto $x$ minimiza $cx$.
Para provar o somente se
,
suponha que $x$ minimiza $cx$.
De acordo com o teorema forte da dualidade,
existe uma solução viável $(y,z)$ do
pl \eqref{lp:min-cost-flow-dual}
tal que $cx=yb+zu$.
De acordo com o lema 4.1,
temos
-
$x_{vw}=0$ ou $y_w - y_v + z_{vw} = c_{vw}$ e
-
$x_{vw}=u_{vw}$ ou $z_{vw} = 0$
para cada arco $vw$.
Como $y_w-y_v + z_{vw} \leq c_{vw}$ e $z_{vw}\leq 0$
em \eqref{lp:min-cost-flow-dual},
as condições 1 e 2 estão satisfeitas. ■
Para algumas aplicações,
é conveniente colocar as condições 1 e 2 do teorema 4.2
na seguinte forma:
para cada arco $vw$,
-
se $x_{vw} > 0$ então
$y_w - y_v \geq c_{vw}$ e
-
se $x_{vw} \lt u_{vw}$ então $y_w - y_v \leq c_{vw}$.
Custo reduzido
A desigualdade $y_w - y_v \leq c_{vw}$
na condição 2 é familiar:
ela caracteriza os arcos relaxados no problema do caminho de custo mínimo
(seção 1.2).
O número $c_{vw}-(y_w-y_v)$
é conhecido como custo reduzido
do arco $vw$.
Usaremos a notação
\[
\cy_{vw} := c_{vw} - (y_w - y_v)\text{.}
\]
[Essa notação deixa a desejar
pois esconde a dependência do potencial $y$.
Quem sabe deveríamos escrever $c^y_{vw}$.]
Com essa notação, poderemos apresentar as condições de otimalidade do
teorema 4.2
de forma mais memorável:
para cada arco $e$,
-
se $x_{e} > 0$ então
$\cy_{e} \leq 0$ e
-
se $x_{e} \lt u_{e}$ então $\cy_{e} \geq 0$.
Isso tem a seguinte consequência:
se $0 \lt x_{e} \lt u_{e}$ então
$\cy_{e} = 0$.
Exemplo 4.2:
Considere a rede $(D,b,u,c)$ do
exemplo 4.1.
Veja novamente a matriz de adjacências de $D$
e o vetor de demandas $b$.
À direita de $b$ temos um potencial $y$.
Mais à direita, um fluxo viável $x$
(diferente dos fluxos do
exemplo 4.1),
o custo $c$ dos arcos,
e o custo reduzido $\cy$ associado a $y$.
\[
\begin{array}[t]{*{5}{r}rr}
& p & v & w & q & b & y \\[0.5ex]
p & - & 1 & 1 & - & \he -2 & \he -10 \\
v & - & - & 1 & 1 & -1 & -40 \\
w & - & - & - & 1 & +1 & 0 \\
q & - & - & - & - & +2 & -10
\end{array}
\hspace{4ex}
\begin{array}[t]{l*{5}{r}}
& pv & pw & vw & vq & wq \\[0.5ex]
\hline
u & 3 & 3 & 3 & 3 & 3 \\
x & 2 & 0 & 3 & 0 & 2 \\
c & \hb -30 & \hb +80 & \hb +40 & \hb +90 & \hb -10 \\
\cy & 0 & +70 & 0 & +60 & 0
\end{array}
\]
O fluxo $x$ e o potencial $y$ satisfazem as
condições de otimalidade.
Portanto, $x$ é um fluxo ótimo e $y$ é um certificado de otimalidade,
conforme o teorema 4.2.
(Embora isso seja redundante,
podemos calcular o vetor $z$ definido
em \eqref{eq:definition-of-z}
e verificar que $cx = +40 = yb +zu$.)
Exercícios 4.3
-
Seja $y$ um potencial arbitrário numa rede $D(b,u,c)$
e $\cy$ o correspondente custo reduzido.
Mostre que $\cy = c - yA$,
sendo $A$ a matriz de incidências do grafo $G$.
-
★
Custo versus custo reduzido.
Seja $x$ um fluxo que satisfaz $b$ e $y$ é um potencial arbitrário.
Seja $\cy$ o custo reduzido associado a $y$.
Mostre que $\cy x = cx - yb$.
4.4 Ciclos de aumento
Dado um fluxo viável $x$ numa rede
$(D,b,u,c)$,
como obter um novo fluxo viável mais barato?
Usaremos um mecanismo análogo ao dos caminhos de aumento do
algoritmo de Ford–Fulkerson
(seção 2.5).
Para qualquer ciclo $C$
em $D$,
seja $\Eforward(C)$ o conjunto dos
arcos diretos
de $C$ e
$\Ereverse(C)$ o conjunto dos arcos
inversos.
Um ciclo $C$ é compatível com um fluxo viável $x$
se $x_e \lt u_e$ para cada $e$ em $\Eforward(C)$
e $x_e > 0$ para cada $e$ em $\Ereverse(C)$.
A largura de $C$ é o maior número $\epsilon$ tal que
$x_e + \epsilon \leq u_e$ para cada $e$ em $\Eforward(C)$
e $x_e-\epsilon \geq 0$ para cada $e$ em $\Ereverse(C)$.
A operação de enviar $\epsilon$ unidades de fluxo ao longo do ciclo $C$
consiste em
somar $\epsilon$ a $x_e$ para cada $e$ em $\Eforward(C)$
e subtrair $\epsilon$ de $x_e$ para cada $e$ em $\Ereverse(C)$.
Se $\epsilon$ for menor ou igual à largura de $C$,
o envio $\epsilon$ unidades de fluxo ao longo de $C$
produz um novo fluxo viável $x'$.
O custo de $x'$ será
$cx + \epsilon c(C)$,
sendo
\[
c(C) := c(\Eforward(C)) - c(\Ereverse(C))\text{.}
\]
O número $c(C)$ é o custo de $C$.
Se esse custo for negativo e $\epsilon$ for positivo,
o fluxo $x'$ será mais barato que $x$.
Por isso, qualquer ciclo compatível com $x$ que tenha custo negativo é chamado
ciclo de aumento.
(Quem sabe deveríamos dizer ciclo de decremento
,
já que o custo do fluxo diminui.)
Exemplo 4.3:
No exemplo 4.1,
o ciclo induzido por $(v,w,q,v)$
é compatível com o fluxo $x$ e tem largura $1$.
O custo do ciclo é $40-10-90=-60$ e portanto o ciclo é de aumento.
Se enviarmos $1$ unidade de fluxo ao longo desse ciclo
teremos o fluxo viável $x'$ do
exemplo 4.1.
Observe que $cx' = cx - 60\times 1 = 240-60 = 180$.
Ainda no exemplo 4.1,
o ciclo $(p,v,w,p)$ é compatível com o fluxo $x'$
e tem largura $2$.
O custo do ciclo é $-30+40-80=-70$
e portanto trata-se de um ciclo de aumento.
Se enviarmos $2$ unidades de fluxo ao longo desse ciclo
teremos o fluxo viável $x''$ abaixo.
Observe que $cx'' = cx' - 70\times 2 = 180-140 = 40$.
\[
\begin{array}[t]{l@{\quad}rrrrr}
& pv & pw & vw & vq & wq \\[0.5ex]
\hline
c & -30 & +80 & +40 & +90 & -10 \\
x''& 2 & 0 & 3 & 0 & 2
\end{array}
\]
O seguinte teorema mostra que
a ausência de ciclos de aumento caracteriza
fluxos ótimos:
Teorema 4.3 (dos ciclos de aumento)
Um fluxo viável $x$ numa rede $(D,b,u,c)$ é ótimo
se e somente se
não existe ciclo de aumento
para $x$.
Prova:
Considere inicialmente a parte somente se
do teorema.
Suponha que o custo de $x$ é mínimo.
Se existisse um ciclo de aumento, poderíamos usar esse ciclo,
como indicado acima,
para obter um novo fluxo viável de custo menor que $cx$.
Portanto, um tal ciclo não existe.
Agora considere a parte se
do teorema, ou seja,
suponha que não existe ciclo de aumento para $x$.
Gostaríamos de usar os resultados do capítulo 1,
desenvolvidos para caminhos e ciclos
dirigidos,
para mostrar que $x$ tem custo mínimo.
Para fazer isso, será preciso construir uma rede auxiliar
$(D',c')$ que chamaremos residual.
O grafo dirigido residual
$D'$ é definido da seguinte maneira.
O conjunto de nós de $D'$ é $D\cup \conj{r}$,
sendo $r$ um novo nó.
Para cada arco $vw$ de $D$ tal que $x_{vw} \lt u_{vw}$,
há um arco $vw$ de custo $c'_{vw}=c_{vw}$ em $D'$.
Para cada arco $vw$ de $D$ tal que $x_{vw} > 0$,
há um
arco $wv$ de custo $c'_{wv}=-c_{vw}$
em $D'$.
(Se $0 \lt x_{vw} \lt u_{vw}$ então $D'$ tem arcos $vw$ e $wv$.)
Finalmente, para cada nó $v$ de $D$,
o grafo residual $D'$ tem um arco $rv$ de custo $c'_{rv}=0$.
É fácil entender a relação entre $D$ e $D'$:
todo ciclo $C$ em $D$ que é compatível com $x$
corresponde a um ciclo dirigido $C'$ em $D'$, e vice-versa.
Ademais, o custo de $C$ em $D$ é igual ao custo de $C'$ em $D'$.
Submeta a rede $(D',c')$,
com nó inicial $r$,
ao algoritmo de Ford para caminhos dirigidos de custo mínimo
(seção 1.3).
Por hipótese, a rede não tem ciclo dirigido de custo negativo.
Portanto, de acordo com o
teorema de Ford–Bellman
(teorema 1.5),
o algoritmo produzirá um potencial viável,
ou seja, um potencial $y$ tal que $y_w - y_v \leq c'_{vw}$
para cada arco $vw$ de $D'$.
Agora considere as propriedades do potencial $y$
no grafo dirigido original $D$.
Se $x_{vw} \lt u_{vw}$ então $vw$ é um arco de $D'$
e $c'_{vw}=c_{vw}$,
donde $y_w - y_v \leq c_{vw}$,
e portanto o custo reduzido de $vw$ não é negativo:
\[
\cy_{vw} \geq 0\text{.}
\]
Por outro lado, se $x_{vw} > 0$ então $wv$ é um
arco de $D'$ e
$c'_{wv}=-c_{vw}$,
donde $y_v - y_w \leq c'_{wv}$.
Logo $y_w - y_v \geq c_{vw}$,
e portanto
\[
\cy_{vw} \leq 0\text{.}
\]
Assim, o par $(x,y)$ satisfaz as
condições de otimalidade
(seção 4.3).
Isso garante que $x$ é ótimo. ■
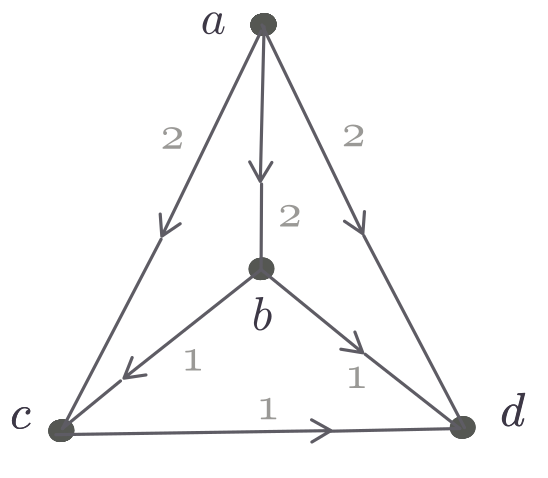
Exemplo 4.4:
Seja $D$ o grafo dirigido descrito abaixo
por sua matriz de adjacências.
À direita da matriz, temos as demandas $b$.
Mais à direita,
as capacidades $u$,
os custos $c$, e um fluxo viável $x$.
O ciclo induzido por $(c,b,a,c)$ é de aumento.
Envie $1$ unidade de fluxo ao longo do ciclo.
O novo fluxo é ótimo?
\[
\begin{array}[t]{*{5}{r}@{\qquad}r}
& a & b & c & d & b \\[0.5ex]
a & - & 1 & 1 & 1 & \he -3 \\
b & - & - & 1 & 1 & +1 \\
c & - & - & - & 1 & +1 \\
d & - & - & - & - & +1
\end{array}
\hspace{6ex}
\begin{array}[t]{l*{6}{r}}
& ab & ac & ad & bc & bd & cd \\[0.5ex]
\hline
u & 9 & 9 & 9 & 9 & 9 & 9 \\
c & \hb +20 & \hb +20 & \hb +20 & \hb +10 & \hb +10 & \hb +10 \\
x & 3 & 0 & 0 & 1 & 1 & 0
\end{array}
\]
(No nosso problema 4.A,
as capacidades dos arcos são finitas.
Mas imagine por um momento que permitíssemos capacidades infinitas.
Então a presença de um ciclo de aumento dirigido —
um ciclo de aumento $C$ com $\Ereverse(C) = \emptyset$ —
levaria a fluxos viáveis de custo arbitrariamente negativo
e tornaria essa instância ilimitada.)
Soluções inteiras
Muitas aplicações precisam de fluxos $x$ que são
inteiros
e de potenciais $y$ que são
inteiros.
Surpreendentemente,
tais fluxos e potencias existem
sempre que os parâmetros da rede são inteiros.
Teorema 4.4 (fluxo inteiro)
Seja $(D,b,u,c)$ uma rede que tem um fluxo viável.
Se $b$ e $u$ são inteiros então existe um fluxo ótimo que é inteiro.
Esboço da prova:
Dentre os fluxos viáveis inteiros,
escolha um fluxo $x$ para o qual $cx$
é o menor possível.
Se existisse um ciclo de aumento para $x$,
poderíamos enviar uma quantidade inteira de fluxo ao longo do ciclo
e assim produzir um novo fluxo viável inteiro
de custo menor que $cx$.
Logo, não existe ciclo de aumento.
Então a prova do teorema dos ciclos de aumento
(teorema 4.3)
mostra que existe um potencial $y$ que satisfaz as
condições de otimalidade.
Logo, $cx \leq cx'$
para todo fluxo viável $x'$,
inteiro ou não.
Portanto, $x$ é ótimo. ■
Teorema 4.5 (dual inteiro)
Seja $x$ um fluxo ótimo numa rede $(D,b,u,c)$.
Se $c$ é inteiro então
o pl \eqref{lp:min-cost-flow-dual}
tem uma solução ótima $(y,z)$ que é inteira.
Prova:
Como mostra a prova do teorema dos ciclos de aumento
(teorema 4.3)
e a análise dos algoritmos de caminhos dirigidos mínimos no capítulo 1,
existe um potencial $y$ tal que,
para cada $v$,
o número $y_v$ é o custo de um caminho dirigido de custo mínimo de $r$ a $v$
na rede
residual $(D',c')$.
Como $c$ é inteiro,
todos esses custos são inteiros.
Assim, o vetor $y$ e vetor $z$ definido
em \eqref{eq:definition-of-z}
são inteiros.
Ademais,
$(y,z)$ satisfaz as condições de otimalidade descritas no
teorema 4.2
e portanto $(y,z)$ é solução ótima do
pl \eqref{lp:min-cost-flow-dual}. ■
Exercícios 4.4
-
★
Seja $x$ um fluxo viável numa rede $(D,b,u,c)$.
Seja $\epsilon$ a largura de um ciclo $C$ compatível com $x$.
Prove que o envio de $\epsilon$ unidades de fluxo ao longo de $C$
produz um novo fluxo viável.
Prove que o custo do novo fluxo é $cx + c(C)\,\epsilon$,
sendo $c(C) := c(\Eforward(C)) - c(\Ereverse(C))$.
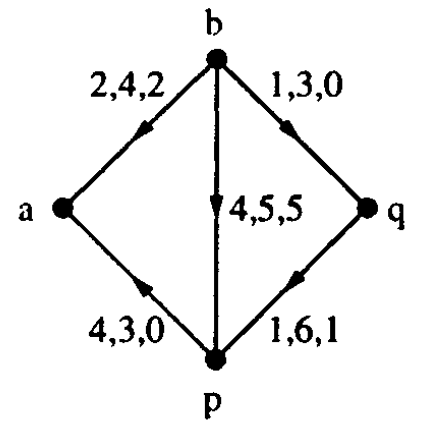
-
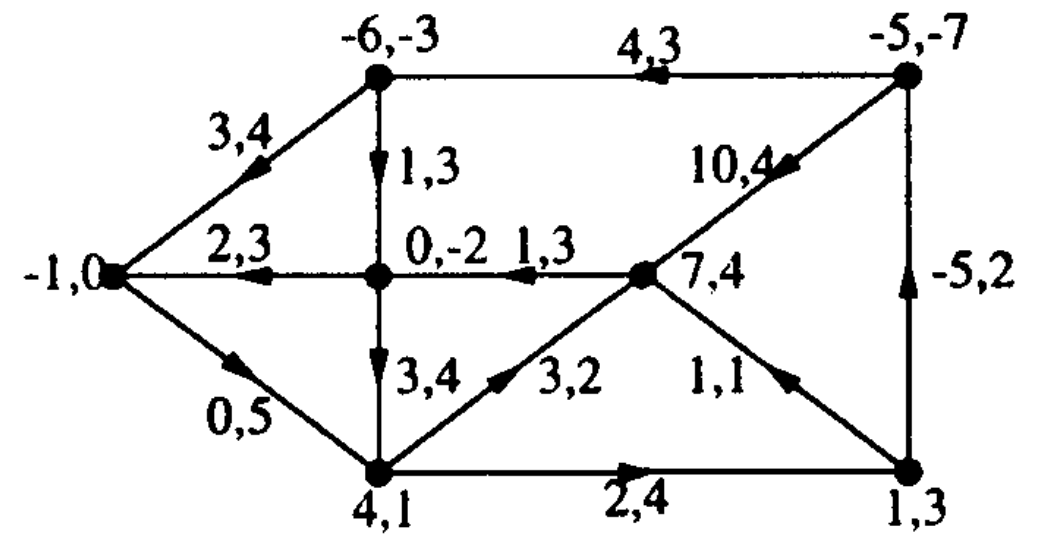
A figura mostra um fluxo viável $x$ numa rede $(D,b,u,c)$.
Os três números ao lado de cada arco $e$ são $c_e,u_e,x_e$.
O custo do fluxo é $cx=25$.
Encontre um ciclo de aumento.
Calcule um fluxo viável de custo menor que o de $x$.
Parte 2: Exiba um fluxo viável de custo mínimo e um potencial que prove
a otimalidade do fluxo.
[CCPS fig.4.1]
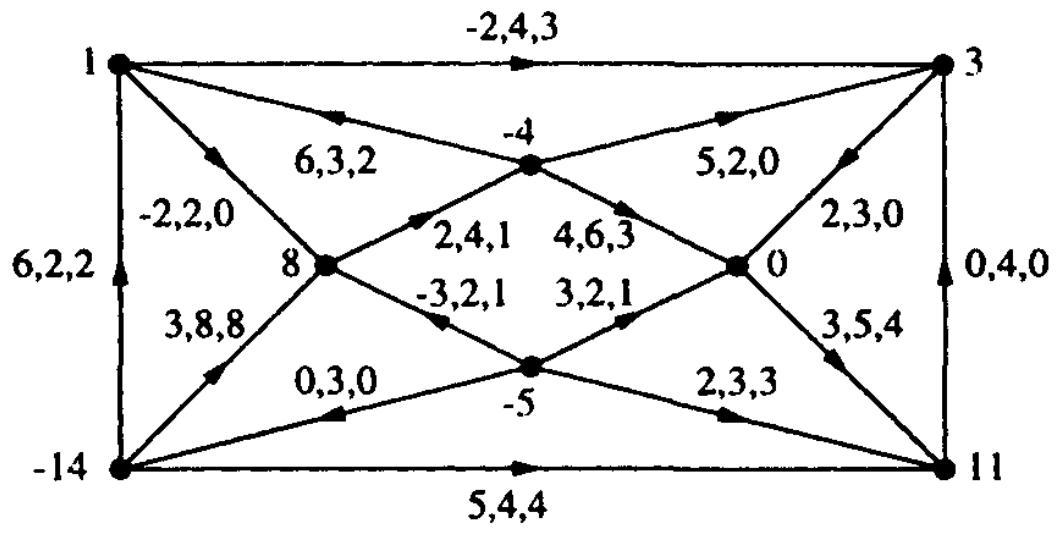
-
Considere a rede de fluxo $(D,b,u,c)$ da figura.
Ao lado de cada nó $v$ vemos a demanda $b_v$.
Ao lado de cada arco $e$ vemos os números $c_e,u_e, x_e$.
Verifique que $x$ é um fluxo viável.
Prove que existe um fluxo viável de custo menor que $cx$
ou prove que $x$ é ótimo.
[CCPS 4.8]
-
Rede residual.
Considere o exemplo 4.1.
Faça uma figura da rede residual correspondente ao fluxo $x$.
Faça uma figura da rede residual correspondente ao fluxo $x'$.
-
Caminhos dirigidos disjuntos.
Sejam $r$ e $s$ dois nós de um grafo dirigido $D$.
Queremos encontrar uma coleção de $k$ caminhos dirigidos de $r$ a $s$,
sem arcos em comum,
que use o menor número possível de arcos.
Formule esse problema como um caso particular
do problema 4.A.
Repita o problema com caminhos dirigidos sem nós em comum
exceto $r$ e $s$.
[AMO 11.8]
-
Considere o grafo dirigido $D$ definido pela matriz de adjacências abaixo.
À direita da matriz, uma função-demanda $b$,
as capacidades $u$ e custos $c$ dos arcos.
Não confunda o nó $b$ com a função-custo $b$.
Encontre um fluxo ótimo $x$ na rede $(D,b,u,c)$.
Encontre um potencial $y$ que satisfaça as condições de otimalidade
do teorema 4.2.
Calcule os custos reduzidos $\cy$.
Faça uma tabela de resultados
para que seja fácil comparar $x$ com $\cy$
e assim conferir a validade das
folgas complementares.
[AMO 9.22]
\[
\begin{array}[t]{*{6}{r}r}
& a & b & c & d & e & b \\[0.5ex]
a & - & 1 & - & - & 1 & -25 \\
b & - & - & 1 & - & 1 & 0 \\
c & - & - & - & 1 & - & 0 \\
d & - & - & - & - & - & +25 \\
e & - & - & 1 & - & 1 & 0
\end{array}
\hspace{5ex}
\begin{array}[t]{l*{7}{r}}
& ab & ae & bc & be & cd & ec & ed \\[0.5ex]
\hline
u & 25 & 20 & 10 & 25 & 20 & 20 & 25 \\
c & \hb +7 & \hb +6 & \hb +4 & \hb +5 & \hb +1 & \hb +2 & \hb +2
\end{array}
\]
-
A figura mostra um potencial $y$ numa rede de fluxo
$(D,b,u,c)$.
Ao lado de cada nó $v$ vemos os números $b_v$ e $y_v$.
Ao lado de cada arco $e$ vemos os números $c_e$ e $u_e$.
Encontre um fluxo viável $x$ que satisfaça as condições de otimalidade
do teorema 4.2.
[CCPS 4.9]
4.5 Algoritmo dos ciclos de aumento
O algoritmo abaixo,
proposto por
Kantorovich
em 1942,
usa ciclos de aumento
para resolver o problema do fluxo de custo mínimo
(problema 4.A)
como sugerido na
seção 4.4.
O algoritmo obtém um primeiro fluxo viável
resolvendo a instância apropriada do problema de Gale
(seção 3.1).
A partir daí,
cada iteração começa com um fluxo viável $x$
e tenta transformar $x$ num fluxo viável $x'$
de custo menor que $cx$.
|
Kantorovich $(D, \ b, \ u, \ c)$
|
|
01
.
$x\larr \text{}$ Gale $(D, \ b, \ u)$
|
|
02
.
se $x$ indefinido
|
|
03
.ooo
então pare
|
|
04
.
repita
|
|
05
.ooo
$C\larr \text{}$ CicloDeAumento $(D, u, c, x)$
|
|
06
.ooo
se $C$ indefinido
|
|
07
.oooooo
então $y \larr \text{}$ Potencial $(D, u, c, x)$
|
|
08
.oooooo
então devolva $x$ e $y$ e pare
|
|
09
.ooo
$\epsilon_1 \larr \min (u_e-x_e : e \in \Eforward(C))$
|
|
10
.ooo
$\epsilon_2 \larr \min (x_e : e \in \Ereverse(C))$
|
|
11
.ooo
$\epsilon \larr \min (\epsilon_1, \epsilon_2)$
|
|
12
.ooo
$x \larr \text{}$ EnviaFluxo $(D,x,C,\epsilon)$
|
A rotina Gale com argumentos $(D,b,u)$
devolve um fluxo $x$ que satisfaz $b$ e respeita $u$.
Se tal fluxo não existe, $x$ fica indefinido.
Na linha 03,
o algoritmo poderia devolver um conjunto de nós
que viola as
condições de Gale
antes de parar.
A rotina CicloDeAumento
na linha 05
devolve um ciclo de aumento
para $x$.
Para implementar a rotina, podemos usar as ideias contidas
na prova do teorema 4.3.
Se não existe ciclo de aumento, $C$ fica indefinido
e o fluxo $x$ é ótimo.
A rotina Potencial
na linha 07 recebe um fluxo ótimo $x$ e
calcula um potencial $y$
que satisfaz as condições de otimalidade
do teorema 4.2.
A rotina EnviaFluxo
na linha 12 atualiza $x$
enviando $\epsilon$ unidades de fluxo ao longo do ciclo $C$,
conforme discussão no início da
seção 4.4.
Número de iterações.
Se os vetores $b$,
$u$, e $c$ são
racionais
e a rede $(D,b,u,c)$ é viável,
o número de iterações
do algoritmo Kantorovich
é finito,
a exemplo do que acontece com o
algoritmo de Ford–Fulkerson para o problema do fluxo máximo
(seção 2.5).
O algoritmo Kantorovich
é útil para redes muito pequenas,
quando pode ser executado com lápis e papel.
Para redes grandes, entretanto, o algoritmo é ineficiente
pois cada iteração consome muito tempo
e o número de iterações
pode aumentar explosivamente
com o número de nós da rede.
Isso acontece pelos mesmos motivos
que tornam ineficiente o algoritmo de Ford–Fulkerson.
Exercícios 4.5
-
Escreva em código a rotina EnviaFluxo.
-
★
Faça um esboço da implementação das rotinas CicloDeAumento
e Potencial
do algoritmo de Kantorovich.
(Sugestão:
As duas rotinas são, na verdade, uma só.
Veja a prova do teorema 4.3
e a seção 1.5.)
-
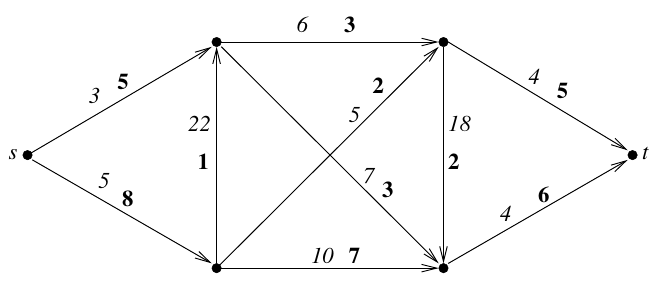
A figura mostra uma rede com capacidades (em negrito) e custos (em itálico)
nos arcos.
Os nós $s$ e $t$ têm demandas $-11$ e $11$ respectivamente.
Os demais nós têm demanda $0$.
Calcule um fluxo viável de custo mínimo.
Prove que o fluxo é ótimo.
[Sch17 4.16i]
4.6 Algoritmo Simplex para redes de transbordo
O algoritmo Kantorovich
(algoritmo dos ciclos de aumento)
é lento e ineficiente.
Para obter um algoritmo mais rápido,
é preciso encontrar uma maneira mais eficiente
de procurar ciclos de aumento.
Discutiremos uma tal maneira ao longo das próximas seções.
A ideia básica é representar o fluxo
por meio de uma subárvore da rede.
Essa ideia será introduzida a seguir no contexto de uma versão simplificada
do problema 4.A,
versão esta conhecida como problema do transbordo.
Uma rede de transbordo
é uma rede de fluxo em que não há restrições de capacidade nos arcos.
[Acredito que a palavra transbordo
poderia ser substituída por baldeação
.
De qualquer forma,
não vale a pena discutir
a etimologia do termo transshipment.]
Mais formalmente,
uma rede de transbordo
(= transshipment network)
é uma rede $(D,b,c)$ em que
$b$ é uma função-demanda nos nós
e $c$ é uma função-custo nos arcos.
O custo de um fluxo $x$ é o número $cx$.
Problema 4.B (do transbordo)
Dada uma rede de transbordo $(D,b,c)$,
encontrar um fluxo que satisfaz $b$
e tem custo mínimo.
Podemos imaginar que o problema 4.B é o caso especial
do problema 4.A
em que $u_e=\infty$ para todo arco $e$.
(É preciso forçar um pouco a imaginação,
pois o enunciado do problema 4.A
não permite arcos de capacidade infinita.)
O primeiro passo para resolver uma instância do problema 4.B
é obter algum fluxo que satisfaz $b$.
Uma rede $(D,b)$
tem um fluxo que satisfaz $b$ se e somente se
-
$b(V) = 0$ e
-
$b(X)\leq 0$ para todo $X\subseteq V$ tal que $\cutin(X)=\emptyset$.
Isso é consequência do que observamos acima
sobre o problema 4.A
bem como de
um exercício na seção 3.1.
Um fluxo $x$ que satisfaz $b$ numa rede de transbordo $(D,b,c)$
é ótimo
se não existe fluxo $x'$
que satisfaz $b$ e tem custo menor que o de $x$.
A adaptação
do teorema 4.2
ao problema 4.B toma a seguinte forma:
Teorema 4.6 (condições de otimalidade)
Um fluxo $x$ que satisfaz $b$ numa rede de transbordo $(D,b,c)$
é ótimo se e somente se
existe um potencial $y$
tal que
-
se $x_{vw} > 0$ então $y_w - y_v = c_{vw}$ e
-
se $x_{vw} = 0$ então $y_w - y_v \leq c_{vw}$
para cada arco $vw$. ■
Deduzir o teorema 4.6 do teorema 4.2
é um
bom exercício.
Fluxos induzidos por árvores.
Vamos procurar uma solução do
problema 4.B
entre os fluxos que fluem
por alguma árvore
da rede.
Começamos por definir a terminologia necessária.
Uma árvore de
um grafo dirigido $D$ é uma
árvore orientada $T$
tal que $V(T)=V(D)$ e $E(T)\subseteq E(D)$.
(Num outro contexto, diríamos que $T$ é uma árvore geradora de $D$.)
Para garantir que as redes em estudo tenham árvores,
restringimos a atenção, daqui em diante,
a redes conexas.
Para redes não conexas,
o problema 4.B
pode ser resolvido separadamente em cada componente conexa.
Uma árvore $T$ da rede $(D,b)$ é viável
se $E(T)$ contém o suporte de algum fluxo que satisfaz $b$.
Como mostra o seguinte lema,
existe no máximo um fluxo dotado dessa propriedade:
Lema 4.7
Numa rede $(D,b)$ com árvore $T$,
se $T$ é viável então
$E(T)$ inclui o suporte de um único
fluxo que satisfaz $b$.
Prova:
Seja $T$ uma árvore viável
e $x$ um fluxo que satisfaz $b$ e cujo suporte é subconjunto de $E(T)$.
Para cada arco $ij$ de $T$,
seja $T_{j}$ a
componente conexa de $T-ij$
que contém $j$.
Em virtude do lema 2.1
no capítulo 2 (com $T_j$ no papel de $R$),
temos
\begin{equation}\label{eq:flow-induced-by-tree}
x_{ij} = b(T_j)
\end{equation}
para cada arco $ij$ de $T$.
Aqui, $b(T_j)$
é uma abreviatura de $b(V(T_j))$
.
Agora suponha que $x'$
é outro fluxo que satisfaz $b$ e tem suporte em $E(T)$.
Se repetirmos o argumento que acabamos de fazer
veremos que $x'_{ij} = b(T_j)$
para cada arco $ij$.
Logo, $x' = x$. ■
Diremos que o único fluxo descrito no lema 4.7
é induzido por $T$.
Para calcular o fluxo induzido por $T$
podemos usar \eqref{eq:flow-induced-by-tree}.
Mas há um algoritmo mais eficiente,
que chamaremos FluxoInduzido.
Ao receber uma árvore viável $T$,
o algoritmo escolhe uma folha $j$ de $T$,
aplica o algoritmo recursivament a $T-j$
depois de modificar $b$,
e finalmente define o valor do fluxo no único arco de $T$ que incide em $j$.
É um bom exercício
escrever o código do algoritmo.
Nem toda árvore de uma rede $(D,b)$ é viável.
Para provar que uma dada árvore $T$ não é viável,
basta observar que $b(V)\neq 0$
ou exibir um arco $ij$ de $T$ tal que
$b(T_j) \not\geq 0$,
sendo $T_{j}$ a
componente conexa de $T-ij$
que contém $j$.
Potenciais induzidos por árvores.
Para certificar a otimalidade de um fluxo,
usamos um potencial apropriado.
Quando o fluxo é induzido por uma árvore,
o potencial pode ser facilmente calculado a partir da árvore.
Dada uma árvore $T$ de uma rede $(D,c)$,
um potencial induzido por $T$
é qualquer potencial $y$
tal que
$c_{ij} = y_j - y_i$
para cada arco $ij$ de $T$, como indicamos a seguir.
É fácil calcular um tal potencial.
Comece com uma folha $j$ de $T$.
Se o único arco incidente a $j$ é $ij$,
calcule o potencial $y$ de $T-j$
e depois estenda esse potencial a $T$
adotando $y_j := y_i+c_{ij}$.
Se o único arco incidente a $j$ for $ji$,
calcule o potencial $y$ de $T-j$
e depois estenda esse potencial a $T$
adotando $y_j := y_i - c_{ji}$.
Vamos nos referir a esse algoritmo como
PotencialInduzido.
Formalizar o algoritmo é um
bom exercício.
Um potencial induzido por uma árvore é quase único:
se $y$ e $y'$ são dois potenciais induzidos
então a diferença $y_i-y'_i$ é a mesma para todos
os nós $i$.
Como trabalhamos apenas com a diferença de potencial entre nós,
podemos viver com a ilusão de que existe um só potencial induzido
e trocar a expressão um potencial induzido
pela expressão o potencial induzido
.
O potencial induzido por uma árvore mede
os custos de caminhos na árvore,
como mostraremos a seguir.
O custo
de um caminho $P$ numa rede $(D,c)$ é
o número $c(P) := \text{}$ $c(\Eforward(P)) - c(\Ereverse(P))$,
sendo $\Eforward(P)$ o conjunto dos arcos diretos
de $P$ e
$\Ereverse(P)$ o conjunto dos arcos inversos.
Lema 4.8
Suponha que $y$ é o potencial induzido por uma árvore $T$ de numa rede $(D,c)$.
Para quaisquer dois nós $r$ e $s$ de $T$ tem-se
$y_s-y_r = c(P)$,
sendo $P$ o único caminho simples
de $r$ a $s$ em $T$.
Prova:
Se $P$ tem um só nó então a afirmação é trivialmente verdadeira.
Agora suponha que $P = (v_0,e_0,v_1,e_1,\ldots,e_{k-1},v_k)$
com $k > 0$.
Para cada nó $v_i$,
seja $y_i$ uma abreviatura de $y_{v_i}$
e $c_i$ uma abreviatura de $c_{e_i}$.
Seja $P'$
o caminho $P-v_k$ e suponha, a título de hipótese de indução,
que $y_{k-1} - y_0 = \text{}$ $c(P')$.
Se $e_{k-1}$ é um arco direto de $P$,
ou seja, se $e_{k-1} = v_{k-1}v_k$,
então
$c(P) = \text{}$ $c(P') + c_{k-1}
= \text{}$ $y_{k-1} - y_0 + y_k - y_{k-1}
= \text{}$ $y_k - y_0$.
Se $e_{k-1}$ é um arco inverso de $P$,
ou seja, se $e_{k-1} = v_k v_{k-1}$,
então
$c(P) = \text{}$ $c(P') - c_{k-1}
= \text{}$ $y_{k-1} - y_0 - (y_{k-1} - y_k)
= \text{}$ $y_k - y_0$. ■
Para trazer a ideia
de circuito de aumento
para o presente contexto,
é preciso estabelecer a relação entre o potencial induzido
e o custo de ciclos que têm apenas um arco fora de uma dada árvore.
Faremos isso no lema 4.9 abaixo,
que decorre do lema 4.8.
Dada uma árvore $T$ de $D$ e um arco $vw$ de $E(D)\setm E(T)$,
o ciclo fundamental
de $T+vw$
é o único ciclo do grafo $T+vw$ no qual o arco $vw$ é
direto.
O custo desse ciclo fundamental é igual ao
custo reduzido
$c_{vw}-y_w+ y_v$
de $vw$:
Lema 4.9
Suponha que $y$ é o potencial induzido por uma árvore $T$ de uma rede $(D,c)$
e seja $\cy$ o correspondente custo reduzido.
Então $\cy_{ij}=0$ para todo arco $ij$ de $T$ e
$\cy_{vw}=c(C)$
para todo arco $vw$ fora de $T$,
sendo $C$ o ciclo fundamental de $T+vw$.
Prova:
Por definição de $y$, temos $\cy_{ij}=0$ para todo arco $ij$ de $T$.
Agora tome um arco $vw$ que não pertence a $T$.
Seja $P$ o caminho de $w$ a $v$ em $T$.
É claro que $C = P+vw$.
Pelo lema 4.8,
$y_v - y_w = \text{}$ $C(P)$.
Logo,
$c(C) = \text{}$ $c(P) + c_{vw}
= \text{}$ $y_v - y_w + c_{vw}
= \text{}$ $\cy_{vw}$. ■
Algoritmo Simplex-para-transbordo
O terreno está preparado para um algoritmo que resolve o
problema 4.B
trabalhando apenas com fluxos em árvores.
O algoritmo, que chamaremos Simplex-para-transbordo
(= TransshipmentSimplex),
pode ser visto como uma versão especializada do
algoritmo Simplex
de programação linear
(seção C.4).
O algoritmo Simplex-para-transbordo
recebe uma rede de transbordo $(D,b,c)$
tal que $D$ é conexo e $b(V)=0$ e devolve
-
um fluxo $x$ e um potencial $y$ que satisfazem as
condições de otimalidade enunciadas no teorema 4.6, ou
-
a informação de que a rede não tem fluxo que satisfaz $b$,
ou
-
a informação de que a rede não tem fluxo que satisfaz $b$ e tem custo mínimo.
|
TransshipmentSimplex $(D, \ b, \ c)$
|
|
01
.
$T \larr \text{}$ ÁrvoreViável $(D, \ b)$
|
|
02
.
repita
|
|
03
.ooo
$x \larr \text{}$ FluxoInduzido $(T, b)$
|
|
04
.ooo
$y \larr \text{}$ PotencialInduzido $(T, c)$
|
|
05
.ooo
seja $\cy$ o custo reduzido associado a $y$
|
|
06
.ooo
se $\cy\geq 0$
|
|
07
.oooooo
então devolva $x$ e $y$ e pare
|
|
08
.ooo
escolha um arco $e$ tal que $\cy_{e} \lt 0$
|
|
09
.ooo
seja $C$ o ciclo fundamental de $T+e$
|
|
10
.ooo
$\epsilon \larr \min\,(x_h : h \in \Ereverse(C) )$
|
|
11
.ooo
se $\epsilon =\infty$
|
|
12
.oooooo
então pare
|
|
13
.ooo
escolha $h$ em $\Ereverse(C)$ tal que $x_h = \epsilon$
|
|
14
.ooo
$T \larr T + e - h$
|
No começo de cada iteração (linha 02),
$T$ é uma árvore viável da rede.
No fim da linha 05,
$x$ é o fluxo induzido por $T$,
$y$ é o potencial induzido por $T$,
e $\cy_e=0$ para todo arco $e$ de $T$.
No linha 07, $x$ e $y$ satisfazem as condições
de otimalidade enunciadas no teorema 4.6
e portanto $x$ é um fluxo ótimo.
No fim da linha 09,
o custo de $C$ é negativo
em virtude do lema 4.9.
Na linha 11,
a condição $\epsilon=\infty$ é equivalente a $\Ereverse(C) = \emptyset$
e portanto
o ciclo $C$ é dirigido,
o que mostra
que a rede não tem fluxo de custo mínimo.
Na linha 13,
$C$ é um ciclo de aumento.
Se enviarmos $\epsilon$ unidades de fluxo
ao longo de $C$,
o valor do fluxo no arco $h$ será reduzido a zero.
Na linha 14,
o arco $h$ é removido de $T$ e
o arco $e$ é acrescentado a $T$.
No fim da linha 14,
$T$ é uma árvore viável.
(Por quê?)
Durante a linha 14,
o número $\epsilon \cy_{vw}$ é implicitamente subtraído do
custo do fluxo $x$.
No fim da linha 14,
poderíamos atualizar
os valores de $x$, $y$,
e $\cy$
evitando assim a necessidade de recalculá-los no início da iteração seguinte
(linhas 03 a 05 do código).
(No caso de $x$, por exemplo,
bastaria enviar $\epsilon$ unidades de fluxo ao longo do ciclo $C$.)
Resta discutir a linha 01.
Esta é a parte suja do algoritmo.
A rotina ÁrvoreViável
deve produzir uma árvore viável,
conhecida como solução inicial
,
ou decidir que uma tal árvore não existe
e apresentar um conjunto de nós
que viola a
condições de Gale
da seção 3.1.
Não há uma maneira limpa de implementar a rotina
ÁrvoreViável.
Adotaremos o truque sujo clássico de
forçar
a existência de uma árvore viável.
Para isso,
suporemos que, em relação a um certo nó $r$ da rede,
-
existe um arco $vr$ para cada nó $v \neq r$ tal que $b(v) \lt 0$ e
-
existe um arco $rw$ para cada nó $w \neq r$ tal que $b(w) \geq 0$.
Essas hipóteses garantem uma árvore viável trivial:
o conjunto de arcos da árvore é $E_1 \cup E_2$,
sendo $E_1 := \conj{vr : b(v) \lt 0}$
e $E_2 := \conj{rw : b(w) \geq 0}$.
Essa árvore inicial é viável uma vez que, por hipótese, $b(V)=0$.
Se a rede não tiver todos os arcos exigidos por (a) e (b),
basta acrescentar os arcos faltantes atribuindo-lhes
custo $\infty$;
diremos que esses arcos são artificiais.
(É bem verdade que a formulação do problema 4.B
supõe que todos os custos são finitos,
mas vamos aceitar esse desvio sem fazer escândalo.
Poderíamos também trocar $\infty$ por um número suficientemente grande.)
Se o algoritmo devolver um fluxo
cujo suporte contém arcos artificiais,
saberemos que a rede original
(sem os arcos artificiais)
não tem fluxo que satisfaz $b$.
Exemplo 4.5:
Considere a rede de transbordo $(D,b,c)$ descrita a seguir.
O grafo dirigido $D$ é dado por sua matriz de adjacências.
A função-demanda $b$ e os custos $c$ dos arcos são dadas nas tabelas.
\[
\begin{array}[t]{*{5}{r}r}
& p & v & w & q & b \\[0.5ex]
p & - & 1 & 1 & - & \he -3 \\
v & - & - & 1 & 1 & +2 \\
w & - & - & - & 1 & -1 \\
q & - & - & - & - & +2
\end{array}
\hspace{4ex}
\begin{array}[t]{*{5}{r}}
& pv & pw & vw & vq & wq \\[0.5ex]
\hline
c & \hb +10 & \hb +30 & \hb +10 & \hb +10 & \hb +10
\end{array}
\]
Suponha que a primeira iteração do algoritmo
TransshipmentSimplex
começa a árvore $T$
indicada em
magenta
na tabela abaixo.
A tabela também registra o fluxo $x$ e o potencial $y$ induzidos por $T$,
bem como os custos reduzidos $\cy$.
O custo do fluxo é $cx=70$.
\[
\begin{array}[t]{l@{\quad}rrrrr}
& \bo{pv} & \bo{pw} & vw & vq & \bo{wq} \\[0.5ex]
\hline
x & 2 & 1 & 0 & 0 & 2 \\
\cy & 0 & 0 & \hb -10 & \hb -20 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
p & 0 \\
v & +10 \\
w & +30 \\
q & +40
\end{array}
\]
O algoritmo escolhe o arco $vw$
e envia $1$ unidade de fluxo ao longo do ciclo induzido por $(v,w,p,v)$.
O novo fluxo terá custo $cx=70-10\times 1=60$.
O arco $vw$ é acrescentado a $T$ e
o arco $pw$ é retirado de $T$.
A segunda iteração começa com a árvore $T$ indicada abaixo em
magenta.
A tabela dá o fluxo induzido $x$,
o potencial induzido $y$,
e o custo reduzido $\cy$.
O fluxo tem custo $cx=60$.
\[
\begin{array}[t]{l@{\hspace{6ex}}rrrrr}
& \bo{pv} & pw & \bo{vw} & vq & \bo{wq} \\[0.5ex]
\hline
x & 3 & 0 & 1 & 0 & 2 \\
\cy & 0 & \hb +10 & 0 & \hb -10 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
p & 0 \\
v & +10 \\
w & +20 \\
q & +30
\end{array}
\]
O algoritmo escolhe o arco $vq$
e envia $1$ unidade de fluxo ao longo do ciclo $(v,q,w,v)$.
O novo fluxo terá custo $cx=60-10\times 1=50$.
A terceira iteração começa a árvore $T$,
o fluxo $x$, e o potencial $y$ indicados a seguir:
\[
\begin{array}[t]{l@{\quad}rrrrr}
& \bo{pv} & pw & vw & \bo{vq} & \bo{wq} \\[0.5ex]
\hline
x & 3 & 0 & 0 & 1 & 1 \\
\cy & 0 & 0 & \hb +10 & 0 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
p & 0 \\
v & +10 \\
w & +10 \\
q & +20
\end{array}
\]
Como $\cy\geq 0$,
a execução do algoritmo termina.
Para detetar eventuais erros de cálculo
cometidos durante a execução do algoritmo,
convém verificar que $cx=yb$.
Número de iterações.
No fim da linha 14,
o custo do fluxo induzido por $T$
é $cx + \epsilon\cy_{e}$,
sendo $\cy_{e} \lt 0$
(veja a seção 4.4
e o lema 4.9).
Se $\epsilon > 0$,
o novo fluxo será mais barato que o anterior
e assim o algoritmo terá feito algum progresso.
Se $\epsilon = 0$,
o fluxo não se altera,
embora a árvore $T$ seja modificada.
Se isso acontece, a iteração é considerada degenerada.
É claro que uma iteração é degenerada se a árvore $T$
no início da iteração tiver um arco vazio,
ou seja, um arco $e$ tal que $x_e=0$.
Diremos que uma tal árvore é degenerada.
É possível, no pior caso,
que o algoritmo comece com uma árvore $T_0$,
execute algumas iterações degeneradas,
e volte à árvore $T_0$.
Essa sequência de iterações pode então se repetir
para sempre e a execução do algoritmo não para mais.
Portanto,
TransshipmentSimplex
não é um algoritmo no sentido pleno da palavra.
Mesmo que não tenhamos iterações degeneradas, entretanto,
o número de iterações pode ser muito grande
pois o algoritmo pode ser levado a examinar todas as árvores da rede.
Felizmente, esses cenários de pior caso são muito raros.
Na prática,
o número de iterações é relativamente pequeno.
Por isso, o algoritmo é bastante usado em aplicações no mundo real.
Viabilidade forte.
Apesar das considerações que acabamos de fazer,
é desejável evitar
que o número iterações seja infinito.
Para isso, basta que
no início de cada iteração
a árvore viável $T$ seja mais que viável,
no sentido que passamos a definir.
Antes de começar a execução do algoritmo,
escolha um nó $r$ (arbitrário mas fixo) para fazer o papel de raiz.
No início de cada iteração, para cada nó $j$,
seja $P_j$ o único caminho simples de $r$ a $j$ em $T$.
A árvore (viável) $T$ é considerada fortemente viável
se o fluxo induzido por $T$ tem a seguinte propriedade:
cada arco vazio de $T$ aponta para longe de $r$
, ou seja,
se $ij$ é um arco vazio de $T$ então $ij$ é um
arco direto
de $P_j$.
Suponha agora que $T$ é fortemente viável no início de uma iteração.
Para que a árvore $T{-}e{+}h$
no início da linha 14 do código também seja fortemente viável,
é preciso escolher o arco $h$
na linha 13
do código como passamos a explicar.
Seja $s$ o nó de $C$ que está mais próximo de $r$ em $T$,
isto é, o último nó comum aos caminhos $P_v$ e $P_w$.
Percorra o ciclo fundamental $C$
a partir de $s$ e
escolha para $h$
\begin{equation}\label{eq:transshipment:leaving-arc-rule}
\text{o primeiro arco em
$\Ereverse(C)$ que tenha $x_h=\epsilon$.}
\end{equation}
Com isso,
a árvore $T{+}e{-}h$ será fortemente viável.
Se $T$ é fortemente viável no início de todas as iterações,
a execução de TransshipmentSimplex
termina depois de um número finito de iterações.
Resta apenas encontrar uma maneira de
fazer com que a primeira árvore viável
(linha 01
do código) seja fortemente viável.
Isso é um bom exercício.
Exemplo 4.6:
Considere a rede de transbordo $(D,b,c)$ descrita a seguir.
(Não confunda o nó $b$ com a função-demanda $b$.)
O grafo dirigido $D$ é dado por sua matriz de adjacências.
Complete a figura usando o gabarito de posição dos nós.
A função-demanda $b$ e os custos $c$ dos arcos são dados nas tabelas.
\[
\begin{array}[t]{*{7}{r}r}
& a & b & c & d & e & f & b \\[0.5ex]
a & - & 1 & 1 & - & - & - & \he -4 \\
b & - & - & - & - & 1 & - & 0 \\
c & - & - & - & 1 & 1 & - & -1 \\
d & - & 1 & - & - & - & 1 & 0 \\
e & - & - & - & - & - & 1 & +1 \\
f & - & - & - & - & - & - & +4
\end{array}
\hspace{6ex}
\begin{array}[t]{l@{\quad}rrrrrrrr}
& ab & ac & be & cd & ce & db & df & ef \\[0.5ex]
\hline
c & \hb +20 & \hb +50 & \hb +60 & \hb +30 & \hb +30 & \hb +30 & \hb +20 & \hb +30
\end{array}
\]
\[
\begin{array}[t]{@{\hspace{20ex}}c@{\hspace{3ex}}c@{\hspace{5ex}}c@{\hspace{3ex}}c}
& & & \\[-10.0ex]
& b\hg & e & \\[1.7ex]
a\hf & & & \hf f \\[1.7ex]
& c\hg & d & \\[-1.5ex]
&
\end{array}
\]
A primeira iteração do algoritmo
TransshipmentSimplex
começa com a árvore $T$ indicada abaixo em
magenta.
A tabela dá o fluxo induzido $x$,
o potencial induzido $y$,
e o correspondente custo reduzido $\cy$.
O custo do fluxo é $cx=560$.
\[
\begin{array}[t]{l@{\quad}rrrrrrrr}
& \bo{ab} & ac& \bo{be}& \bo{cd}& ce& \bo{db}& df& \bo{ef}\\[0.5ex]
\hline
x & 4 & 0& 5& 1& 0& 1& 0& 4\\
\cy & 0 & \hb +90& 0& 0& \hb -90& 0& \hb -100& 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
a & +10 \\
b & +30 \\
c & -30 \\
d & 0 \\
e & +90 \\
f & \hb +120
\end{array}
\]
O algoritmo escolhe o arco $ce$
e envia $1$ unidade de fluxo ao longo do ciclo induzido por $(c,e,b,d,c)$.
Os arcos $cd$ e $db$ ficam vazios.
O primeiro sai da árvore mas o segundo continua na árvore.
O novo fluxo tem custo $cx = \text{}$ $560-90\times 1 = \text{}$ $470$.
A segunda iteração começa com os dados a seguir.
A árvore viável é degenerada.
\[
\begin{array}[t]{l@{\quad}rrrrrrrr}
& \bo{ab}& ac& \bo{be}& cd&\bo{ce}& \bo{db}& df& \bo{ef}\\[0.5ex]
\hline
x & 4& 0& 4& 0& 1& 0& 0& 4\\
\cy & 0& 0& 0& \hb +90& 0& 0& \hb -100& 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
a & +10 \\
b & +30 \\
c & +60 \\
d & 0 \\
e & +90 \\
f & \hb +120
\end{array}
\]
O algoritmo escolhe o arco $df$
e portanto o ciclo $(d,f,e,b,d)$.
Apenas $0$ unidades de fluxo podem ser enviadas ao longo do ciclo.
A iteração é degenerada.
O fluxo $x$ não se altera
mas o arco $df$ é arescentado a $T$ e
o arco $db$ é retirado em $T$.
A terceira iteração começa com os dados indicados a seguir:
\[
\begin{array}[t]{l@{\quad}rrrrrrrr}
& \bo{ab}& ac& \bo{be}& cd&\bo{ce}& db& \bo{df}& \bo{ef}\\[0.5ex]
\hline
x & 4& 0& 4& 0& 1& 0& 0& 4\\
\cy & 0& 0& 0& \hb -10& 0& \hb +100& 0& 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
a & -90 \\
b & -70 \\
c & -40 \\
d & 0 \\
e & -10 \\
f & +20
\end{array}
\]
O algoritmo escolhe o arco $cd$
e envia $1$ unidade de fluxo ao longo do ciclo $(c,d,f,e,c)$.
O novo fluxo tem custo $cx=470 - 10\times 1 = 460$.
A quarta iteração começa com os seguintes dados:
\[
\begin{array}[t]{l@{\quad}rrrrrrrr}
& \bo{ab}& ac& \bo{be}&\bo{cd}& ce& db& \bo{df}& \bo{ef}\\[0.5ex]
\hline
x & 4& 0& 4& 1& 0& 0& 1& 3\\
\cy & 0& \hb -10& 0& 0& \hb +10& \hb +100& 0& 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
a & -90 \\
b & -70 \\
c & -30 \\
d & 0 \\
e & -10 \\
f & +20
\end{array}
\]
O algoritmo escolhe o arco $ac$
e envia $3$ unidades de fluxo ao longo do ciclo $(a,c,d,f,e,b,a)$.
O novo fluxo tem custo $cx=460 - 10\times 3 = 430$.
A quinta iteração começa com os seguintes dados:
\[
\begin{array}[t]{l@{\quad}rrrrrrrr}
& \bo{ab}& \bo{ac}& \bo{be}&\bo{cd}& ce& db& \bo{df}& ef\\[0.5ex]
\hline
x & 1& 3& 1& 4& 0& 0& 4& 0\\
\cy & 0& 0& 0& 0& 0& \hb +90& 0& \hb +10
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
a & -80 \\
b & -60 \\
c & -30 \\
d & 0 \\
e & 0 \\
f & +20
\end{array}
\]
Como $\cy\geq 0$, a execução do algoritmo termina.
Exemplo 4.7:
Considere a rede de transbordo $(D,b,c)$ descrita a seguir.
O grafo dirigido $D$ é dado por sua matriz de adjacências.
(Faça uma figura.)
Os custos $c$, o potencial $y$,
e o custos reduzidos $\cy$ foram omitidos.
Adote o nó $r$ como raiz e suponha que $\cy_{ij} \lt 0$.
\[
\begin{array}[t]{*{8}{r}r}
& r & i & j & k & l & p & q & b\\[0.5ex]
r & - & - & - & - & 1 & - & - & \hf -2\\
i & - & - & 1 & - & - & - & 1 & -1\\
j & - & - & - & - & - & - & - & +1\\
k & - & - & 1 & - & - & - & - & +1\\
l & - & - & - & 1 & - & 1 & - & 0\\
p & - & - & - & - & - & - & - & +1\\
q & - & - & - & - & - & 1 & - & 0
\end{array}
\hspace{4ex}
\begin{array}[t]{l@{\quad}rrrrrrr}
& rl & ij & kj & lk & lp & qp & iq \\[0.5ex]
\hline
x & 2 & 0 & 1 & 2 & 0 & 1 & 1
\end{array}
\]
Execute uma iteração do
TransshipmentSimplex
começando com a árvore viável
$T = \text{}$ $\conj{rl,kj, lk, lp, qp,iq}$.
Note que $T$ é fortemente viável.
O algoritmo escolhe o arco $ij$ pois $\cy_{ij} \lt 0$.
O ciclo fundamental de $T+ij$ é $(i,j,k,l,p,q,i)$.
A largura do ciclo é $1$.
Qualquer um dos arcos $kj$,
$qp$, $iq$ poderia ser removido de $T$
para dar lugar a $ij$.
Para garantir que a nova árvore viável seja fortemente viável,
o algoritmo remove o arco $qp$.
Exemplo 4.8:
Considere a rede de transbordo $(D,b,c)$ descrita a seguir.
O grafo dirigido $D$ é dado por sua matriz de adjacências.
(Faça uma figura.)
A função-demanda $b$ e os custos $c$ dos arcos são dadas nas tabelas.
Adote o nó $p$ como raiz.
[CCPS fig.4.10]
\[
\begin{array}[t]{*{5}{r}rr}
& p & v & w & q & b \\[0.5ex]
p & - & - & - & - & +1\\
v & 1 & - & 1 & 1 & \he -1\\
w & 1 & - & - & 1 & -1\\
q & - & - & - & - & +1
\end{array}
\hspace{4ex}
\begin{array}[t]{*{6}{r}}
& vp & wp & vw & vq & wq \\[0.5ex]
\hline
c & \hb +10 & \hb +10 & \hb +10 & \hb +10 & \hb +20
\end{array}
\]
A primeira iteração do
TransshipmentSimplex
começa com a árvore viável $T$ indicada a seguir
(os arcos de $T$ estão destacados em
magenta).
A árvore é degenerada mas fortemente viável.
O fluxo induzido tem custo $cx=30$.
\[
\begin{array}[t]{l@{\quad}rrrrr}
& \bo{vp} & wp & \bo{vw} & vq & \bo{wq} \\[0.5ex]
\hline
x & 1 & 0 & 0 & 0 & 1 \\
\cy & 0 & \hb +10 & 0 & \hb -20 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
p & 0 \\
v & \hb -10 \\
w & 0 \\
q & +20
\end{array}
\]
O algoritmo escolhe o arco $vq$.
A sequência de nós do correspondente ciclo fundamental,
escrita a partir do nó mais próximo da raiz,
é $(v,q,w,v)$.
Como $\epsilon=0$, a iteração é degenerada.
O envio de $0$ unidades de fluxo ao longo do ciclo
não altera o fluxo mas altera a árvore viável.
A segunda iteração começa com uma árvore viável
degenerada mas fortemente viável.
O fluxo induzido tem custo $cx=30$.
\[
\begin{array}[t]{l@{\quad}rrrrr}
& \bo{vp} & wp & vw & \bo{vq} & \bo{wq} \\[0.5ex]
\hline
x & 1 & 0 & 0 & 0 & 1 \\
\cy & 0 & \hb -10 & \hb +20 & 0 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
p & 0 \\
v & \hb -10 \\
w & -20 \\
q & 0
\end{array}
\]
O algoritmo escolhe o arco $wp$.
O correspondente ciclo fundamental,
a partir do nó mais próximo da raiz, é $(p,v,q,w,p)$.
Temos $\epsilon=1$ e o arco $vp$ faz o papel de $h$.
O envio de $1$ unidade de fluxo ao longo do ciclo
produz um novo fluxo de custo $cx=30-10\times 1=20$.
A terceira iteração começa com uma árvore viável
degenerada mas fortemente viável.
(Se a iteração anterior tivesse escolhido $h=wq$,
a árvore não seria fortemente viável.)
\[
\begin{array}[t]{l@{\quad}rrrrr}
& vp & \bo{wp} & vw & \bo{vq} & \bo{wq} \\[0.5ex]
\hline
x & 0 & 1 & 0 & 1 & 0 \\
\cy & \hb +10 & 0 & 0 & 0 & 0
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
p & 0 \\
v & 0 \\
w & \hb -10 \\
q & +10
\end{array}
\]
Como $\cy\geq 0$, a execução do algoritmo termina.
Exercícios 4.6
-
★
Prove o teorema 4.6
a partir do
teorema 4.2.
-
Em que condições uma instância do problema do transbordo
(problema 4.B) é inviável?
Em que condições é ilimitada?
-
Seja $x$ um fluxo
num grafo dirigido conexo $D$.
Suponha que todo ciclo (dirigido ou não) em $D$
tem um arco vazio,
isto é, um arco $e$ tal que $x_e=0$.
Mostre que existe uma árvore $T$ de $D$
tal que o suporte de $x$ é subconjunto de $E(T)$.
-
★
Fluxo viável implica fluxo arbóreo.
Suponha que uma rede conexa $(D,b)$ tem um fluxo que satisfaz $b$.
Prove que o suporte de algum fluxo que satisfaz $b$
é subconjunto de alguma árvore da rede.
Parte 2:
Suponha que uma rede conexa $(D,b,c)$ tem um fluxo ótimo
e prove que o suporte de algum fluxo ótimo
é subconjunto de alguma árvore da rede.
-
★
Complete os detalhes da prova do
lema 4.7.
-
★
FluxoInduzido.
Escreva um algoritmo que receba uma árvore viável $T$
de uma rede $(D,b)$
e devolva o único fluxo em $T$ que satisfaz $b$.
-
Escreva uma versão
completa
do algoritmo
FluxoInduzido.
O algoritmo deve receber uma árvore $T$ e uma função-demanda $b$
tal que $b(V)=0$
e devolver o único fluxo em $T$ que satisfaz $b$
ou uma prova de que tal fluxo não existe.
A prova consiste em um arco $kl$ de $T$ tal que
$b(T_l) \lt 0$.
-
★
PotencialInduzido.
Escreva um algoritmo que receba uma árvore $T$
de uma rede $(D,c)$
e devolva o potencial induzido por $T$.
Mais exercícios
-
Custo de arcos artificiais,
Seja $(D,b,c)$ uma rede de transbordo com arcos arficiais.
Atribua custo
$1 + |V| \max \conj{|c_e| : e\in E}$ a cada arco artificial.
Suponha que o algoritmo
Simplex-para-Transbordo
termina com fluxo não nulo em algum arco artificial.
Mostre que a instância original do problema
(antes da introdução dos arcos artificiais)
não tem fluxo viável.
[CCPS 4.21]
-
Resolva a instância do problema do transbordo indicada na figura.
Use o algoritmo TransshipmentSimplex.
Os números junto aos nós são as demandas $b$.
Os números nos arcos são os custos $c$.
Comece com o fluxo $x$ induzido pela árvore viável $T$
representada pelas linhas contínuas.
[CCPS 4.22]
-
Solução inicial no
Simplex-para-transbordo.
Escreva uma implementação da rotina ÁrvoreViável
sob as hipóteses (a) e (b).
Prove que sua implementação está correta.
-
Solução inicial no Simplex-para-transbordo.
Discuta a seguinte ideia de implementação da rotina ÁrvoreViável.
1. Calcule um fluxo $x$ em $(D,b)$ que satisfaz $b$
como sugere a seção 3.1,
que trata do problema de Gale.
(É assim que começa o
algoritmo Kantorovich.)
2. Se houver um ciclo em que todos os arcos têm fluxo positivo,
envie fluxo ao longo do ciclo de modo a anular o fluxo em algum arco.
3. Repita o processo até que
o suporte de $x$ seja subconjunto do conjunto de arcos de uma árvore).
4. Extraia uma árvore $T$ do suporte de $x$.
-
Árvore fortemente viável inicial.
Encontre uma maneira de construir a árvore viável $T$
na linha 01
de TransshipmentSimplex
de modo que ela seja fortemente viável.
-
Mostre como representar $T$ de maneira eficiente
no algoritmo TransshipmentSimplex.
Mostre como os valores $x$,
$y$, e $\cy$ podem ser calculados,
a cada iteração, a partir dos valores de $x$,
$y$, e $\cy$
na iteração anterior
(evitando assim que os valores sejam
calculadas diretamente a partir de $T$).
[CCPS 4.23]
-
No algoritmo TransshipmentSimplex,
suponha que $T$ é fortemente viável no início de uma iteração
em que $\epsilon=0$.
Mostre que $h$ estará em $P_w$ (e não em $P_v$).
Mostre que $h$ será o último arco direto vazio de $P_w$.
-
Exemplo 4.6.
Analise o exemplo 4.6.
Adote o nó $d$ como raiz e verifique que
no início de cada iteração do algoritmo
a árvore viável $T$ é fortemente viável.
-
Mostre que toda árvore não-degenerada
é fortemente viável.
-
De fortemente viável a fortemente viável.
Suponha que $T$ é fortemente viável e
$h$ é escolhido de acordo com a
regra \eqref{eq:transshipment:leaving-arc-rule}.
Mostre que no início da linha 14 de TransshipmentSimplex
a árvore viável $T{+}e{-}h$ é fortemente viável.
-
O número de iterações é finito.
Seja $r$ a raiz de $D$ e defina $y$
na linha 04
de TransshipmentSimplex
de modo que $y_r=0$
(e portanto $y_v=c(P_v)$
para cada $v$).
Suponha que $T$ é fortemente viável no início de uma iteração
e seja $Y$ o valor da soma $\sum (y_v : v\in V)$
no fim da linha 04.
Suponha que $\epsilon$ é nulo nessa iteração.
Prove que na próxima iteração,
no fim da linha 04,
a soma $\sum (y_v : v\in V)$ será menor que $Y$.
Deduza daí que o número de iterações degeneradas é finito.
4.7 Algoritmo Simplex para redes arbitrárias
O algoritmo Simplex-para-redes
(= Network Simplex)
é uma generalização
do algoritmo Simplex-para-transbordo
discutido na seção anterior.
O algoritmo
resolve o problema do fluxo de custo mínimo
(problema 4.A).
Esse é
o algoritmo mais usado na prática para resolver o problema.
Tripartições arbóreas e fluxo induzido.
Para apresentar o Simplex-para-redes,
é preciso generalizar os conceitos que introduzimos para tratar do
Simplex-para-transbordo.
Uma tripartição arbórea
de um grafo $D$ é um terno
$(T,L,U)$ em que $T$ é uma árvore de $D$
e $(E(T),L,U)$
é uma partição
do conjunto de arcos de $D$.
Para garantir que as redes em estudo tenham árvores,
restringimos a atenção
a redes conexas
daqui em diante.
Como no início do capítulo,
um fluxo numa rede $(D,b,u)$
é viável
se satisfaz $b$ e respeita $u$.
Em relação a um fluxo viável $x$,
diremos que um arco $e$ está vazio se $x_e=0$
e está cheio se $x_e=u_e$.
(Se $u_e = 0$,
o arco $e$ está simultaneamente vazio e cheio.
Pode ser conveniente
remover tais arcos da rede —
o que certamente não afeta o problema 4.A —
e passar a supor que $u_e > 0$ para cada arco $e$.)
Uma tripartição arbórea $(T,L,U)$ da rede $(D,b,u)$ é viável
se algum fluxo viável em $(D,b,u)$
deixa todos os arcos de $L$ vazios
e todos os arcos de $U$ cheios.
(Nada impede que esse mesmo fluxo deixe alguns arcos de $T$ vazios
e alguns arcos de $T$ cheios.)
Segue do lema 4.7 que existe no máximo um tal fluxo:
Lema 4.10
Para qualquer tripartição arbórea $(T,L,U)$ de uma rede
$(D,b,u)$,
existe no máximo um fluxo viável
que deixa os arcos de $L$ vazios
e os arcos de $U$ cheios. ■
Dizemos que o único fluxo viável a que se refere o lema 4.10
é induzido por $(T,L,U)$,
Se o fluxo induzido deixa algum arco de $T$ vazio ou algum arco cheio,
dizemos que a tripartição $(T,L,U)$ é degenerada.
Potenciais induzidos por tripartições arbóreas.
Numa rede $(D,c)$,
um potencial $y$ é induzido por
uma tripartição arbórea $(T,L,U)$
se $c_{vw} = y_w - y_v$ para cada arco $vw$ de $T$.
Tal como
no caso das redes de transbordo,
toda tripartição arbórea tem um potencial induzido
e esse potencial é essencialmente único.
Seja $(T,L,U)$ uma tripartição arbórea do grafo $D$.
Para cada $e$ em $L$,
o ciclo fundamental
de $T+e$ é o único ciclo em $T+e$ no qual
$e$ é um arco direto.
Para cada $e$ em $U$,
o ciclo fundamental
de $T+e$ é o único ciclo em $T+e$ no qual
$e$ é um arco inverso.
O seguinte lema generaliza o lema 4.9:
Lema 4.11
Seja $(T,L,U)$ uma tripartição arbórea de uma rede $(D,b,c)$.
Seja $y$ o potencial induzido pela tripartição
e $\cy$ o custo reduzido
associado a $y$.
Para cada arco $e$,
-
se $e \in T$ então $\cy_{e}=0$,
-
se $e \in L$ então $\cy_{e}=c(C)$,
-
se $e \in U$ então $\cy_{e}=-c(C)$,
sendo $C$ o ciclo fundamental de $T+e$.
Esboço da prova:
Basta generalizar a prova do lema 4.9,
que trata apenas de redes de transbordo. ■
Algoritmo Simplex-para-redes
Ao receber uma rede $(D,b,u,c)$ com $D$ conexo e $b(V)=0$,
o algoritmo Simplex-para-redes
produz uma tripartição arbórea viável $(T,L,U)$
e um potencial $y$ que satisfazem as condições
-
$\cy_{e} = 0$ para $e$ em $T$,
-
$\cy_{e} \geq 0$ para $e$ em $L$,
-
$\cy_{e} \leq 0$ para $e$ em $U$,
sendo $\cy$ o custo reduzido associado a $y$.
De acordo com teorema 4.2
(veja a formulação alternativa
do teorema),
o fluxo $x$ induzido por $(T,L,U)$ é ótimo.
O algoritmo consiste em
duas cópias do algoritmo Simplex-para-transbordo
trabalhando simultaneamente:
uma cópia normal
, idêntica à discutida na seção anterior,
que cuida da restrição $x\geq 0$,
e uma cópia invertida
que cuida da restrição $x \leq u$.
|
NetworkSimplex $(D,b,u,c)$
|
|
01
.
$(T,L,U) \larr \text{}$ TripartiçãoArbóreaViável $(D,b,u)$
|
|
02
.
se $(T,L,U)$ é indefinida
|
|
03
.ooo
então pare
|
|
04
.
repita
|
|
05
.ooo
seja $x$ o fluxo induzido por $(T,L,U)$
|
|
06
.ooo
seja $y$ um potencial induzido por $(T,L,U)$
|
|
07
.ooo
seja $\cy$ o custo reduzido associado a $y$
|
|
08
.ooo
se $\cy_e\geq 0$ quando $e\in L$ e $\cy_e\leq 0$ quando $e\in U$
|
|
09
.oooooo
então devolva $(T,L,U)$ e $y$ e pare
|
|
10
.ooo
escolha $e \in L$ tal que $\cy_{e} \lt 0$
ou $e \in U$ tal que $\cy_{e} > 0$
|
|
11
.ooo
seja $C$ o ciclo fundamental de $T+e$
|
|
12
.ooo
$\epsilon \larr \min\,(u_h - x_h : h \in \Eforward(C) )$
|
|
13
.ooo
$\epsilon' \larr \min\,(x_h : h \in \Ereverse(C) )$
|
|
14
.ooo
se $\epsilon \lt \epsilon'$
|
|
15
.oooooo
então escolha $h$ em $\Eforward(C)$ tal que $u_h-x_h = \epsilon$
|
|
16
.oooooo
senão escolha $h$ em $\Ereverse(C)$ tal que $x_h = \epsilon'$
|
|
17
.ooo
$T \larr T + e - h$
|
|
18
.ooo
se $e\in L$ então $L\larr L-e$ senão $U \larr U-e$
|
|
19
.ooo
se $h\in \Eforward(C)$ então $U \larr U+h$ senão $L\larr L+h$
|
No começo de cada iteração (linha 04),
$(T,L,U)$ é uma tripartição arbórea viável.
A rotina
TripartiçãoArbóreaViável
na linha 01
deve produzir uma tripartição arbórea viável.
Se tal tripartição não existe, a rede não admite fluxo viável.
Não há uma maneira limpa de implementar a rotina
TripartiçãoArbóreaViável.
Um truque sujo clássico consiste em escolher um nó $r$,
arbitrário mas fixo,
e acrescentar à rede
(a) um arco $vr$ para cada nó $v \neq r$ tal que $b(v) \lt 0$ e
(b) um arco $rw$ para cada nó $w \neq r$ tal que $b(w) \geq 0$.
Esses arcos artificiais devem ter capacidade infinita e custo infinito.
Feito isso,
considere a árvore $T$ com conjunto de arcos $E_1 \cup E_2$,
sendo $E_1 := \conj{vr : b(v) \lt 0}$
e $E_2 := \conj{rw : b(w) \geq 0}$,
e seja $L$ conjunto $E(D)\setm E(T)$.
Agora, $(T, L, \emptyset)$ é uma tripartição arbórea viável.
Se o algoritmo NetworkSimplex
terminar com um fluxo
cujo suporte contém arcos artificiais,
saberemos que a rede original
não tem fluxo viável.
Exemplo 4.9:
Considere a rede $(D,b,u,c)$ descrita a seguir.
O grafo dirigido $D$ é dado por sua matriz de adjacências.
A função-demanda $b$ e os custos $c$ dos arcos são dadas nas tabelas.
\[
\begin{array}[t]{*{5}{r}r}
& p & v & w & q & b \\[0.5ex]
p & - & 1 & 1 & - & \he -4 \\
v & - & - & 1 & 1 & 0 \\
w & - & - & - & 1 & +2 \\
q & - & - & - & - & +2
\end{array}
\hspace{4ex}
\begin{array}[t]{l@{\quad}rrrrr}
& pv & pw & vw & vq & wq \\[0.5ex]
\hline
u & \infty & \infty & 1 & \infty & \infty \\
c & \hb +10 & \hb +20 & +8 & \hb +20 & \hb +20
\end{array}
\]
A primeira iteração do algoritmo
NetworkSimplex
começa com
a tripartição arbórea viável $(T,L,U)$ indicada abaixo.
Os arcos de $T$ estão indicados em
magenta,
os arcos de $L$ estão sublinhados,
e $U$ é vazio.
Veja na tabela o fluxo $x$ e o potencial $y$ induzidos pela tripartição.
\[
\begin{array}[t]{*{6}{r}}
& \bo{pv} & \bo{pw} &\undr{vw} & \bo{vq} &\undr{wq} \\[0.5ex]
\hline
x & 2 & 2 & 0 & 2 & 0 \\
\cy & 0 & 0 & -2 & 0 & \hb +10
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
p & 0 \\
v & +10 \\
w & +20 \\
q & \hb +30
\end{array}
\]
O algoritmo escolhe o arco $vw$
e envia $1$ unidades de fluxo ao longo do ciclo induzido por $(v,w,p,v)$.
O arco $vw$ fica cheio e é transferido de $L$ para $U$.
A tripartição $(T,L,U)$ não se altera.
O novo fluxo terá custo $cx=100-2\times 1=98$.
A segunda iteração começa com a tripartição arbórea $(T,L,U)$
indicada abaixo
com uma barra acima
dos arcos de $U$.
[Pode ser necessário aumentar ou diminuir
(Ctrl+ ou Ctrl-)
o tamanho da fonte no seu browser
para que a barra fique visível.]
O fluxo tem custo $cx=98$.
\[
\begin{array}[t]{l@{\quad}rrrrr}
& \bo{pv} & \bo{pw} & \ovr{vw}& \bo{vq} &\undr{wq} \\[0.5ex]
\hline
x & 3 & 1 & 1 & 2 & 0 \\
\cy & 0 & 0 & -2 & 0 & \hb +10
\end{array}
\hspace{6ex}
\begin{array}[t]{rr}
& y \\[0.5ex]
p & 0 \\
v & +10 \\
w & +20 \\
q & \hb +30
\end{array}
\]
Como $\cy_e\geq 0$ para todo $e$ em $L$
e $\cy_e\leq 0$ para todo $e$ em $U$,
o fluxo $x$ é ótimo
e a execução do algoritmo termina.
Por via dúvidas, convém verificar que
$cx = \text{}$ $yb+zu$.
(Essa é uma boa maneira de detetar eventuais erros de cálculo
cometido durante a execução do algoritmo.)
O vetor $z_e=\min\,\left(0,\,\cy_e\right)$ está indicado abaixo:
\[
\begin{array}[t]{*{6}{r}}
& \bo{pv} & \bo{pw} & \ovr{vw} & \bo{vq} & \undr{wq} \\[0.2ex]
\hline
z & 0 & 0 & \hb -2 & 0 & 0
\end{array}
\hspace{20ex}
\]
Portanto, $cx = 98 = 100-2 = yb+zu$,
como deveria ser.
Consumo de tempo.
O algoritmo NetworkSimplex,
tal como TransshipmentSimplex,
pode executar um número infinito de iterações,
embora tal evento seja muito raro na prática.
Para evitar que isso aconteça, basta fazer o seguinte:
(i) antes de iniciar a execução do algoritmo,
escolha um nó $r$ como raiz;
(ii) adote $y_r=0$ em todas as iterações;
(iii) tome providências para que a tripartição arbórea $(T,L,U)$
seja fortemente viável no início de cada iteração.
Uma tripartição arbórea viável $(T,L,U)$
é fortemente viável se
o fluxo induzido pela tripartição tem a seguinte propriedade:
cada arco $ij$ de $T$ que está vazio aponta para longe da raiz
(ou seja, $ij$ é um arco de $P_j\,$),
e cada arco $ij$ de $T$ que está cheio
aponta na direção da raiz
(ou seja, $ij$ é um arco de $P_i\,$).
Exercícios 4.7
-
Seja $(D,b)$ uma rede conexa.
Mostre que um fluxo $x$ é induzido por uma tripartição arbórea
se e somente se
todo ciclo de $D$ tem um arco vazio ou um arco cheio
(ou ambos).
-
★
Fluxo viável implica fluxo arbóreo.
Suponha que uma rede $(D,b,u)$ tem um fluxo viável
e prove que a rede também tem um fluxo viável
induzido por alguma tripartição arbórea.
Parte 2:
Suponha que uma rede $(D,b,u,c)$ tem um fluxo ótimo
e prove que a rede também tem um fluxo ótimo
induzido por alguma tripartição arbórea.
[CCPS 4.27]
-
Prove o lema 4.10.
-
Escreva um algoritmo que receba uma tripartição arbórea $(T,L,U)$
de uma rede $(D,b,u)$,
decida se a tripartição é viável,
e em caso afirmativo calcule o fluxo induzido pela tripartição.
-
Dê condições necessárias e suficientes para que
uma tripartição arbórea $(T,L,U)$ seja viável.
Mais exercícios
-
★
Prove o lema 4.11.
-
★
É possível ter $h=e$ no começo da linha 17
do NetworkSimplex?
Como o algoritmo se comporta nesse caso?
-
Tripartição arbórea inicial.
Eis um truque feio mas efetivo para calcular
a tripartição $(T,L,U)$ inicial na linha 01
de NetworkSimplex.
Antes de invocar o algoritmo,
acrescente a $D$ um novo nó $r$
e novos arcos da seguinte maneira:
para cada nó $v$ com $b_v \lt 0$,
acrescente um novo arco $vr$;
para cada $v$ tal que $b_v \geq 0$,
acrescente um novo arco $rv$.
Seja $B^+$ o conjunto dos novos arcos do tipo $vr$
e $B^-$ o conjunto dos novos arcos do tipo $rv$.
Cada novo arco deve ter custo $M$ e capacidade $\infty$.
A constante $M$ deve ser positiva e muito grande.
Seja $T:=B^+\cup B^-$.
Adote fluxo $x_{vr}:=-b_v$ para cada $vr\in B^+$
e fluxo $x_{rv}:=b_v$ para cada $rv\in B^-$.
Faça $L$ igual ao conjunto dos arcos originais
e faça $U$ igual a $\emptyset$.
A tripartição arbórea $(T,L,U)$ é fortemente viável se tomarmos $r$ como raiz.
Como o custo $M$ é muito grande,
nenhum dos arcos artificiais estará na árvore
produzida por NetworkSimplex.