Algoritmos para Grafos  |  Índice

Algoritmo de Bellman-Ford

Este capítulo discute um algoritmo para do problema da CPT (= cheapest-paths tree), que já foi apresentado no capítulo Caminhos de custo mínimo.

Vale lembrar que uma árvore de caminhos baratos, ou CPT, é uma sub­árvore radicada geradora T de G tal que todo caminho em T que começa na raiz é mínimo em G.  Como observamos no capítulo introdutório, uma instância do problema tem solução se e somente se (1) todos os vértices de G estão ao alcance de s e (2) o grafo não tem ciclos negativos.  Para escamotear a primeira condição, podemos trabalhar com o sub­grafo induzido pelos vértices que estão ao alcance de s. Já a segunda condição é fundamental e não pode ser contornada.

Um algoritmo para o problema foi descoberto por R. Bellman e L.R. Ford e publicado em 1956-58.  O algoritmo parece muito simples, mas é lento e a análise da sua correção é difícil.

O algoritmo

Ao receber um grafo G com custos nos arcos e um vértice s, o algoritmo de Bellman-Ford procura encontrar uma CPT de G que tenha raiz s.  Para simplificar a discussão do algoritmo, suporemos que todos os vértices de G estão ao alcance de s.  O algoritmo calculará o vetor de pais de uma CPT ou anunciará que o grafo tem um ciclo negativo.

A ideia é simples:  o algoritmo mantém um potencial dist[ ] sobre o conjunto de vértices e relaxa, sistematicamente, os arcos que estão tensos em relação a esse potencial.

Para discutir os detalhes, convém introduzir o seguinte conceito. Se G tem V vértices, uma V-permutação do conjunto de arcos de G é a concatenação de V permutações dos arcos de G, ou seja, uma sequência da forma P₀ P₁ … P_V−1 em que cada P_i é uma permutação do conjunto de arcos de G.  Podemos supor que as V permutações são iguais, embora isso não seja essencial. Por exemplo, se G tem 4 vértices e arcos a, b, c, então

a  b  c  a  b  c  a  b  c  a  b  c

é uma V-permutação dos arcos de G.

O algoritmo de Bellman-Ford começa por escolher alguma V-permutação do conjunto de arcos de G. Digamos que a V-permutação escolhida é  a₀ a₁ a₂ … a_VA−1,  sendo V o número de vértices e A o número de arcos de G.  O algoritmo processa a₀, depois a₁, depois a₂, e assim por diante.  Cada iteração começa com um arco a_k , um potencial dist[ ], e um vetor pa[ ] que leva vértices em vértices.  A primeira iteração começa com k ≡ 0, dist[s] ≡ 0, pa[s] ≡ s, e com dist[v] ≡ ∞ e pa[v] indefinido para todo v distinto de s.  A k-ésima iteração consiste no seguinte:

1. sejam v e w as pontas inicial e final do arco a_k
2. seja c o custo de v-w
3. se v-w está tenso então faça
   • dist[w] = dist[v] + c
   • pa[w] = v

Ao final desse processo — ou seja, quando k ≡ VA — temos duas alternativas:  se todos os arcos estão relaxados então pa[ ] é o vetor de pais de uma CPT com raiz s e dist[ ] é o vetor das distâncias em G a partir de s.  Senão, G tem um ciclo negativo e portanto não tem CPT.

Convém lembrar que, por definição, um arco v-w está tenso em relação a dist[ ] se dist[v]+c < dist[w], está relaxado se dist[v]+c ≥ dist[w], e está justo se dist[v]+c ≡ dist[w].  É claro que todo arco v-w que tem dist[v] ≡ ∞ está relaxado e todo arco v-w que tem dist[v] < ∞ e dist[w] ≡ ∞ está tenso.

Para facilitar o discussão do algoritmo, é útil quebrar a sequência de VA iterações em V grupos de A iterações. Diremos que cada grupo é uma rodada. Portanto, cada rodada é uma sequência de A iterações que processa uma permutação do conjunto de arcos de grafo. A primeira rodada processa os arcos  a₀ a₁ … a_V−1;  a segunda rodada processa os arcos  a_V a_V+1 … a_2V−1;  e assim por diante.

Durante a execução do algoritmo, a relaxação de um arco tenso v-w diminui o valor de dist[w] e assim pode deixar tenso algum arco w-x que já havia sido relaxado numa rodada anterior.  Com isso, cada arco pode ser relaxado várias vezes, uma vez em cada rodada.

Exemplo A.  Considere o problema de encontrar uma CPT com raiz 4 no grafo definido pela listas de adjacência abaixo. Todos os vértices estão ao alcance de 4. O custo de cada arco está indicado entre parênteses.

0: 4  (2)
1: 0  (2)
2: 1 (-9)
3: 2  (2)
4: 3  (2)

Como o grafo tem 5 vértices, o algoritmo executa 5 rodadas. Suponha que cada rodada examina os arcos na ordem  0-4 1-0 2-1 3-2 4-3.  Veja o estado dos vetores dist[ ] e pa[ ] no início de cada rodada, com * no lugar de ∞ e - no lugar de valores indefinidos:

 dist[]           pa[]
 0  1  2  3  4    0  1  2  3  4  
  	                              
 *  *  *  *  0    -  -  -  -  4
 *  *  *  2  0    -  -  -  4  4  
 *  *  4  2  0    -  -  3  4  4  
 * -5  4  2  0    -  2  3  4  4  
-3 -5  4  2  0    1  2  3  4  4  
-3 -5  4  2 -1    1  2  3  4  0

Ao final desse processo, o arco 4-3 continua tenso, o que indica a existência de um ciclo negativo. (O ciclo negativo em questão é 4-3-2-1-0-4. Note que todos os arcos desse ciclo têm a forma pa[x]-x.)

 0 — 1 — 4 
   / \    
 2 — 3   

Exemplo B.  Considere o grafo com custos nos arcos descrito abaixo. Todos os vértices estão ao alcance de 0. Vamos submeter o grafo ao algoritmo de Bellman-Ford para procurar uma CPT com raiz 0.

0-1 1-2 2-3 3-1 1-4
  5   1   1  -4   5

(Estamos especialmente interessados em um caminho mínimo de 0 a 4.)  O algoritmo executa 5 rodadas, pois o grafo tem 5 vértices. Suponha que cada rodada examina os arcos na ordem  0-1 1-2 2-3 3-1 1-4.  Veja o estado dos vetores dist[ ] e pa[ ] no início de cada rodada:

dist[]           pa[]
0  1  2  3  4    0  1  2  3  4  

0  *  *  *  *    0  -  -  -  -
0  3  6  7  8    0  3  1  2  1  
0  1  4  5  6    0  3  1  2  1  
0 -1  2  3  4    0  3  1  2  1  
0 -3  0  1  2    0  3  1  2  1  
0 -5 -2 -1  0    0  3  1  2  1

O arco 1-2 continua tenso. Portanto o grafo tem algum ciclo negativo ao alcance de 0.  (O ciclo negativo em questão é 1-2-3-1. Todos os arcos desse ciclo têm a forma pa[x]-x.)  A propósito, note que o caminho 0-1-2-3-1-4 tem custo mínimo, mas não é simples.  Note também que o sub­grafo descrito por pa[ ] não é uma árvore radicada.

Análise

Antes de começar a análise do algoritmo de Bellman-Ford, faremos três observações preliminares.  Suponha que C é um caminho com origem x e término y e denote por  cst(C)  o custo do caminho.  As três observações se referem ao estado de relaxação ou tensão dos arcos de C em relação a um potencial dist[ ] definido sobre os vértices do grafo:

1. Se cada arco de C está relaxado então cst(C) ≥ dist[y] − dist[x].
2. Se cada arco de C está tenso ou justo então cst(C) ≤ dist[y] − dist[x].
3. Se cada arco de C está justo então cst(C) ≡ dist[y] − dist[x].

Para provar essas observações basta fazer um cálculo análogo ao que usamos na prova da cota inferior para distâncias entre vértices no capítulo Caminhos de custo mínimo.  Um caso particular importante de A: se C for um caminho fechado cujos arcos estão todos relaxados então cst(C) ≥ 0.

Podemos agora começar a análise da correção do algoritmo de Bellman-Ford. Para provar que o algoritmo produz o resultado prometido, é preciso observar que certas propriedades valem no início de cada iteração. Dois desses invariantes são óbvios e podem ser enunciadas já. No início de cada iteração, denotaremos por S o conjunto dos vértices x para os quais pa[x] está definido, ou, equivalentemente, para os quais dist[x] < ∞. Então, para todo x em S,

1. pa[x] está em S;
2. se x ≠ s então pa[x] ≠ x.

Os demais invariantes são menos óbvios. Para enunciá-los, é preciso introduzir algumas definições.

No início de cada iteração, seja  F  o sub­grafo de G cujo conjunto de vértices é S e cujos arcos são todos os que têm a forma pa[x]-x com x em S.  Esse sub­grafo está bem definido graças ao invariante i.  É claro que nenhum vértice de F tem grau de entrada maior que 1. Ademais, todo vértice de F exceto possivelmente s tem grau de entrada igual a 1, graças ao invariante ii.  (Portanto, F é um grafo funcional, embora não seja necessariamente uma floresta radicada.)

No início de cada iteração, denotaremos por  L  a sequência dos arcos que o algoritmo examinou até esse momento. É claro que L é um segmento inicial da V-permutação  a₀ a₁ a₂ … a_VA−1  adotada antes da primeira iteração.  Diremos que um caminho em G está bem-casado com L se a sequência de arcos do caminho é uma subsequência de L.

Podemos agora enunciar os demais invariantes. No início de cada iteração,

3. para todo caminho C em G com origem s e término z, se C é bem-casado com L então cst(C) ≥ dist[z];
4. todo arco de F está justo ou tenso em relação a dist[ ];
5. todo ciclo em F é negativo;
6. dist[s] ≡ 0 se e somente se pa[s] ≡ s.

(Graças à observação preliminar B acima, o invariante iv garante que cst(C) ≤ dist[y] − dist[x] para qualquer caminho C em F com origem x e término y.  Note, entretanto, que o invariante iii não é consequência da observação preliminar A acima, pois os arcos de C não estão necessariamente relaxados e o lado direito da desigualdade não tem o termo − dist[s].)

Prova da correção.  Podemos agora usar os invariantes para provar que o algoritmo produz o resultado prometido. Suponha que o algoritmo já executou as V rodadas, ou seja, já examinou todos os arcos da V-permutação a₀ a₁ a₂ … a_VA−1.  Nesse momento, L é igual à V-permutação e portanto todo caminho em G com V arcos ou menos está bem-casado com L.  Portanto, todo caminho C de s a um vértice z que tenha no máximo V arcos satisfaz a desigualdade cst(C) ≥ dist[z], de acordo com o invariante iii.  Devemos agora considerar duas possibilidades:

• Possibilidade 1: todos os arcos de G estão relaxados.  Então dist[ ] é um potencial relaxado e portanto G não tem ciclo negativo.  O invariante v garante agora que F não tem ciclo algum e portanto F é topológico.  Segue daí que F é uma floresta radicada.  Em virtude de ii, a única raiz de F é s e portanto F é uma árvore radicada.  A distância em F de s a qualquer vértice x é igual a dist[x] − dist[s], graças ao invariante iv e à observação C acima.  Mas dist[s] ≡ 0, graças ao invariante vi, e portanto podemos afirmar que a distância em F de s a x é exatamente dist[x].  Resta mostrar que F é um sub­grafo gerador.  Seja z um vértice qualquer de G e C um caminho simples em G com origem s e término z. Um tal caminho existe uma vez que, por hipótese, todos os vértices estão ao alcance de s. Como já notamos acima, dist[z] ≤ cst(C), uma vez que C tem menos que V arcos. Segue daí que dist[z] < ∞ e portanto z pertence a F. Esse argumento mostra que F é um sub­grafo gerador.  Finalmente, todas essas propriedades de F mostram que (veja o capítulo Caminhos de custo mínimo) F é uma CPT de G.
• Possibilidade 2: existe um arco tenso em G.  Digamos v-w é um arco tenso e que seu custo é c, donde dist[v] + c < dist[w]. Seja  v₀ ≡ v, v₁ ≡ pa[v₀], v₂ ≡ pa[v₁], e assim por diante. Diremos que a sequência  v₀ v₁ v₂ …  é a regressão de v.  Essa sequência é infinita (graças ao invariante i) e portanto tem termos repetidos. Seja k o menor índice tal que v_k ≡ v_j para algum j < k.  Precisamos provar que j < k−1. Faremos isso por contradição. Suponha então, por um momento, que k ≡ j+1.  Então v_j ≡ v_k ≡ s, de acordo com o invariante ii.  É claro que a sequência  v₀ v₁ v₂ … v_j  não tem termos repetidos. Portanto, essa sequência é o reverso de um caminho simples em F de s a v. Denote esse caminho por C e observe que cst(C) ≤ dist[v] − dist[s], graças ao invariante iv e à observação B acima.  O caminho C não passa por v-w, pois se assim fosse C seria um ciclo e não chegaria a s. Portanto, a concatenação de C com v-w é um caminho. Denotaremos esse caminho por D. (O novo caminho não está necessariamente em F. Por outro lado, w pode ser igual a s, e nesse caso o novo caminho é um ciclo.)  Como C é simples, D tem no máximo V arcos e assim cst(D) ≥ dist[w], como já observamos antes. Por outro lado, cst(D) ≡ cst(C) + c ≤ dist[v] − dist[s] + c. Logo, dist[v] − dist[s] + c ≥ dist[w]. Como o arco v-w está tenso, devemos ter  dist[s] < 0.  Logo, pa[s] ≠ s, conforme o invariante vi. Mas então v_j+1 ≠ v_j , e isso contraria a hipótese k ≡ j+1 que adotamos no início do raciocínio. Essa contradição mostra que devemos ter k > j+1. Portanto, a sequência de vértices  v_j v_j+1 … v_k  é o reverso de um ciclo em T.  Esse ciclo é negativo, em virtude do invariante v.

Concluímos assim que o algoritmo produz o resultado que prometeu: devolve uma CPT de G ou esbarra num ciclo negativo (que prova a inexistência de uma CPT).

Implementação do algoritmo

Nossa implementação do algoritmo de Bellman-Ford supõe que o grafo é representado por listas de adjacência com custos.  Assim, para cada vértice v e cada a em G->adj[v], a relaxação do arco que vai de v a a->w consiste em fazer

      dist[a->w] = dist[v] + a->c; // relaxação
      pa[a->w] = v;

Para evitar trabalho supérfluo, não vamos examinar todos os arco do grafo em cada rodada, pois muitos já estão relaxados desde a rodada anterior. É suficiente examinar os arcos v-w para o quais o valor de dist[v] diminuiu na rodada anterior, pois somente esses arcos podem estar tensos.  Para isso, basta manter uma fila de vértices ativos e inserir um vértice w na fila somente quando algum arco v-w sofrer relaxação. Com isso, em cada iteração, a ponta inicial de todo arco tenso estará na fila.

Para isolar cada rodada da seguinte, a fila tem dois segmentos: o primeiro corresponde à rodada corrente e o segundo corresponde à próxima.  Uma sentinela é inserida na fila para separar o primeiro segmento do segundo; o pseudovértice V é uma sentinela conveniente.  O processamento da fila consiste em examinar os leques de saída de todos os vértices do primeiro segmento e alimentar o segundo segmento. Esse processo é interrompido depois de V rodadas.

/* Recebe um vértice s de um grafo G 
   com custos arbitrários nos arcos
   e supõe que todos os vértices estão ao alcance de s.
   Devolve false 

   se G tem algum ciclo negativo
   e portanto não tem CPT.
   Senão, devolve true
   e armazena em pa[] o vetor de pais de 
   uma CPT de G com raiz s.
   Nesse segundo caso,
   as distâncias a partir de s são armazenadas 
   no vetor dist[].
   (A função supõe que a soma de todos os custos positivos é menor 
   que INT_MAX.
   O código foi inspirado no Programa 21.9
   de Sedgewick.) */

bool GRAPHcptBF( Graph G, vertex s, vertex *pa, int *dist)
{
   QUEUEinit( G->A);
   bool onqueue[1000];
   for (vertex u = 0; u < G->V; ++u)
      pa[u] = -1, dist[u] = INT_MAX, onqueue[u] = false;
   pa[s] = s, dist[s] = 0;
   QUEUEput( s);
   onqueue[s] = true;
   vertex V = G->V; // pseudovértice
   QUEUEput( V); // sentinela
   int k = 0;

   while (true) { 
      vertex v = QUEUEget( );
      if (v < V) {
         for (link a = G->adj[v]; a != NULL; a = a->next) {
            if (dist[v] + a->c < dist[a->w]) {
               dist[a->w] = dist[v] + a->c; 
               pa[a->w] = v;
               if (onqueue[a->w] == false) {
                  QUEUEput( a->w);
                  onqueue[a->w] = true;
               }
            }
         }
      } else {
         if (QUEUEempty( )) return true; // A
         if (++k >= G->V) return false; // B
         QUEUEput( V); // sentinela
         for (vertex u = 0; u < G->V; ++u) 
            onqueue[u] = false;
      }
   }
}

Aa seguintes observações podem ajudar a entender o código:

• A constante INT_MAX representa o infinito. Para que a implementação esteja correta, é preciso que o valor da expressão dist[v] + a->c seja sempre menor que INT_MAX. Para garantir isso, basta exigir que a soma de todos os custos positivos do grafo seja menor que INT_MAX.
• A variável k conta as rodadas. Cada novo valor de k preside uma rodada. Em cada rodada, o algoritmo percorre uma permutação do conjunto de arcos do grafo.
• No ponto A não há ciclo negativo e pa[] descreve uma CPT com raiz s. No ponto B, todos os caminhos com até V arcos já foram examinados mas a fila não ficou vazia; portanto o grafo tem um ciclo negativo.
• Para que a fila de vértices não fique excessivamente longa, um vértice é inserido na fila apenas se já não estiver presente depois da sentinela. Para fazer isso, a implementação consulta o vetor característico onqueue[] do segundo segmento da fila.

A função supõe que todos os vértices estão ao alcance de s. Mas não é necessário testar essa condição antes de invocar a função:  Se essa condição não estiver satisfeita, a função GRAPHcptBF() produzirá uma CPT do sub­grafo induzido pelo conjunto de vértices que estão ao alcance de s  ou  dirá que existe um ciclo negativo ao alcance de s.

 0 
 | 
 1 
 | 
 2 
 | 
 3 
 | 
 4 

Exemplo C.  Considere o grafo com custos nos arcos descrito a seguir. Todos os vértices estão ao alcance de 0. Queremos encontrar uma CPT com raiz 0.

0-1  1-2  2-3  3-4 
 10   10   10   10 

Veja o estado da fila e dos vetores dist[] e pa[] no início de cada iteração controlada pelo  while (true),  com * no lugar de INT_MAX e - no lugar de -1:

       dist[]           pa[]                    
queue  0  1  2  3  4    0 1 2 3 4
              
0 5    0  *  *  *  *    0 - - - -
5 1    0 10  *  *  *    0 0 - - -
1 5    0 10  *  *  *    0 0 - - -
5 2    0 10 20  *  *    0 0 1 - -
2 5    0 10 20  *  *    0 0 1 - -
5 3    0 10 20 30  *    0 0 1 2 -
3 5    0 10 20 30  *    0 0 1 2 -
5 4    0 10 20 30 40    0 0 1 2 3
4 5    0 10 20 30 40    0 0 1 2 3
5      0 10 20 30 40    0 0 1 2 3

Como a fila ficou vazia, o grafo não tem ciclo negativo e o último valor de pa[] descreve uma CPT com raiz 0.

Exemplo D.  Queremos encontrar uma CPT com raiz 0 no grafo com custos nos arcos descrito a seguir. Todos os vértices estão ao alcance de 0.

0-1  1-2  0-3  3-1  0-4  4-5  5-1 
 20   30    9    9    5    5    5

Veja o estado da fila e dos vetores dist[] e pa[] no início de cada iteração controlada pelo  while (true),  com * no lugar de INT_MAX e - no lugar de -1:

          dist[]             pa[]                    
queue     0  1  2  3  4  5   0 1 2 3 4 5
              
0 6       0  *  *  *  *  *   0 - - - - -
6 1 3 4   0 20  *  9  5  *   0 0 - 0 0 -
1 3 4 6   0 20  *  9  5  *   0 0 - 0 0 -
3 4 6 2   0 20 50  9  5  *   0 0 1 0 0 -
4 6 2 1   0 18 50  9  5  *   0 3 1 0 0 -
6 2 1 5   0 18 50  9  5 10   0 3 1 0 0 4
2 1 5 6   0 18 50  9  5 10   0 3 1 0 0 4
1 5 6     0 18 50  9  5 10   0 3 1 0 0 4
5 6 2     0 18 48  9  5 10   0 3 1 0 0 4
6 2 1     0 15 48  9  5 10   0 5 1 0 0 4
2 1 6     0 15 48  9  5 10   0 5 1 0 0 4
1 6       0 15 48  9  5 10   0 5 1 0 0 4
6 2       0 15 45  9  5 10   0 5 1 0 0 4
2 6       0 15 45  9  5 10   0 5 1 0 0 4
6         0 15 45  9  5 10   0 5 1 0 0 4

A fila ficou vazia. Portanto, o grafo não tem ciclo negativo e o último valor de pa[] descreve uma CPT com raiz 0.

 0 
 | 
 1 
 | 
 2 
 | 
 3 
 | 
 4 

Exemplo E.  Queremos encontrar uma CPT com raiz 0 no grafo com custos nos arcos descrito a seguir. Todos os vértices estão ao alcance de 0.

0-1  1-0  1-2  2-1  2-3  3-2  3-4  4-3
 -1   -1   -1   -1   -1   -1   -1   -1

Veja o estado da fila e dos vetores dist[] e pa[] no início de cada iteração controlada pelo while (true):

            dist[]           pa[]                    
queue       0  1  2  3  4    0 1 2 3 4
              
0 5         0  *  *  *  *    0 - - - -
5 1         0 -1  *  *  *    0 0 - - -
1 5         0 -1  *  *  *    0 0 - - -
5 0 2      -2 -1 -2  *  *    1 0 1 - -
0 2 5      -2 -1 -2  *  *    1 0 1 - -
2 5 1      -2 -3 -2  *  *    1 0 1 - -
5 1 3      -2 -3 -2 -3  *    1 2 1 2 -
1 3 5      -2 -3 -2 -3  *    1 2 1 2 -
3 5 0 2    -4 -3 -4 -3  *    1 2 1 2 -
5 0 2 4    -4 -3 -4 -3 -4    1 2 1 2 3
0 2 4 5    -4 -3 -4 -3 -4    1 2 1 2 3
2 4 5 1    -4 -5 -4 -3 -4    1 0 1 2 3
4 5 1 3    -4 -5 -4 -5 -4    1 0 1 2 3
5 1 3      -4 -5 -4 -5 -4    1 0 1 2 3

Depois de cinco rodadas, a fila não ficou vazia. Logo, o grafo tem um ciclo negativo. De fato, 0-1-0 é um ciclo negativo.

   0    
  / \   
 1───2  

Exemplo F.  Considere o grafo completo com custos nos arcos descrito abaixo. Queremos encontrar uma CPT com raiz 0. Todos os vértices estão ao alcance de 0.

0-1  1-0  1-2  2-1  2-0  0-2
 -1   -1   -1   -1   -1   -1

Veja o estado da fila e dos vetores dist[] e pa[] no início de cada iteração controlada pelo while (true):

                dist[]     pa[]                    
queue           0  1  2    0  1  2
              
0 3             0  *  *    0  -  -
3 1 2           0 -1 -1    0  0  0
1 2 3           0 -1 -1    0  0  0
2 3 0 2        -2 -1 -2    1  0  1
3 0 2 1        -3 -2 -2    2  2  1
0 2 1 3        -3 -2 -2    2  2  1
2 1 3 1 2      -3 -3 -3    2  0  0
1 3 1 2 0      -4 -4 -3    2  2  0
3 1 2 0        -5 -4 -4    1  2  1

Depois de três rodadas, a fila não ficou vazia. Logo, o grafo tem um ciclo negativo. De fato, 0-1-2-0 é um ciclo negativo.  (É interessante refazer esse exemplo depois de inibir o efeito do vetor booleano onqueue[] que impede que um vértice seja inserido pela segunda vez no segundo segmento da fila.)

 

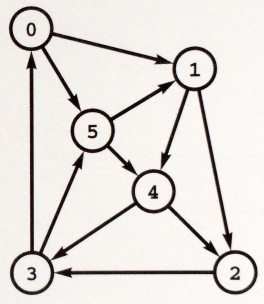
Exemplo G.  A tabela a seguir define um grafo com custos nos arcos. Submeta o grafo à função GRAPHcptBF() com vértice inicial s ≡ 4. Todos os vértices estão ao alcance de s.

0-1 0-5 1-2 1-4 2-3 3-0 3-5 4-2 4-3 5-1 5-4 
 41  29  51  32  50  45 -38  32  36 -29	 21

Veja o estado da fila e dos vetores dist[] e pa[] no início de cada iteração controlada pelo while (true), com * no lugar de INT_MAX e - no lugar de -1:

          dist[]              pa[]                    
queue     0  1   2  3 4  5    0 1 2 3 4 5
        
4 6       *  *   *  * 0  *    - - - - 4 -
6 2 3     *  *  32 36 0  *    - - 4 4 4 -
2 3 6     *  *  32 36 0  *    - - 4 4 4 -
3 6       *  *  32 36 0  *    - - 4 4 4 -
6 0 5    81  *  32 36 0 -2    3 - 4 4 4 3
0 5 6    81  *  32 36 0 -2    3 - 4 4 4 3
5 6 1    81 122 32 36 0 -2    3 0 4 4 4 3
6 1      81 -31 32 36 0 -2    3 5 4 4 4 3
1 6      81 -31 32 36 0 -2    3 5 4 4 4 3
6 2      81 -31 20 36 0 -2    3 5 1 4 4 3
2 6      81 -31 20 36 0 -2    3 5 1 4 4 3
6        81 -31 20 36 0 -2    3 5 1 4 4 3

Depois de cinco rodadas, a fila está vazia. Logo, o grafo não tem ciclo negativo e portanto o vetor dist[] dá as distâncias a partir de 4.

Desempenho.  A função GRAPHcptBF() é quadrática: ela consome V (V+A) unidades de tempo no pior caso.  Ou seja, a função é V vezes mais lenta, no pior caso, que uma busca em largura.

Conclusão

O algoritmo de Bellman-Ford prova o seguinte teorema: Um grafo com custos nos arcos tem uma CPT com raiz s se e somente se todos os vértices estão ao alcance de s e o grafo não tem ciclo negativo.  A propósito, já vimos provas algorítmicas de três outros teoremas da mesma família:

• Um grafo é topológico se e somente se não tem ciclos.
• Um grafo não-dirigido é bipartido se e somente se não tem circuito ímpar.
• Num grafo bipartido, um emparelhamento é máximo se e somente se tem o mesmo tamanho que uma cobertura.

O primeiro teorema é demonstrado pela função GRAPHcycle0(), o segundo é demonstrado pela função UGRAPHtwoColor(), e o terceiro é demonstrado pela função UGRAPHbipMatching() somada ao fragmento de código que calcula uma cobertura mínima.