Algoritmos para Grafos  |  Índice

Caminhos de custo mínimo

Este capítulo é uma introdução geral ao problema do caminho de custo mínimo em grafos com custos arbitrários (positivos e negativos) nos arcos.  (O capítulo Caminhos de comprimento mínimo fez uma introdução análoga no caso em que os arcos não têm custos.)  O problema tem sutilezas que precisam ser bem compreendidas antes que possamos tentar resolvê-lo.  Algoritmos para o problema serão discutidos nos próximos capítulos.

A presença de arcos de custo negativo torna o problema escorragadio e anti-intuitivo. O problema fica especialmente difícil (NP-difícil, no jargão técnico) se o grafo tiver ciclos de custo negativo.

     

Caminhos mínimos e distâncias

Num grafo com custos arbitrários nos arcos, o custo de um caminho é a soma dos custos dos arcos do caminho.  (Convém lembrar que, por definição, caminhos não têm arcos repetidos, e portanto cada arco do caminho contribui uma só vez para o custo.)  Se todos os arcos têm custo 1, por exemplo, o custo do caminho é igual ao seu comprimento.

Um caminho B é mais barato que um caminho C se tiver custo menor que o de C.  Dizemos que um caminho C  tem custo mínimo  se nenhum caminho com a mesma origem e o mesmo término de C é mais barato que C.

Se não houver caminho algum de s a t, o problema não tem solução.  Caso contrário, o problema certamente tem solução, pois o conjunto de diferentes caminhos com origem s e término t é finito, uma vez que caminhos não têm arcos repetidos.

É comum abreviar a expressão caminho de custo mínimo e dizer, simplesmente, caminho mínimo.  (Portanto, o significado da expressão caminho mínimo depende do contexto. Se os arcos do grafo têm custos, a expressão subentende o custo do caminho; senão, subentende o comprimento do caminho, conforme o capítulo Caminhos de comprimento mínimo.)

Se todos os custos são positivos, a relação entre o comprimento e o custo de um caminho é intuitiva: qualquer pedaço do caminho é mais barato que o caminho todo. Se há arcos de custo negativo, a relação entre o comprimento e o custo é traiçoeira, pois um pedaço do caminho pode ser mais caro que o caminho todo.

Arcos de custo negativo ocorrem naturalmente em muitos problemas práticos. Se custo positivo representa gasto, custo negativo representa ganho. Assim, quando há arcos de custo negativo, um caminho mínimo maximiza o lucro.

Distâncias.  A  distância  de um vértice s a um vértice t é o custo de um caminho mínimo com origem s e término t.  A distância de s a t é  d  se e somente se algum caminho de s a t tem custo d e nenhum caminho de s a t tem custo menor que d.

É claro que a distância de s a t é, em geral, diferente da distância de t a s.  Por isso, dizemos distância de s a t e não distância entre s e t.

Se todos os arcos do grafo têm custo positivo e t está ao alcance de s, a distância de s a t é positiva.  Se há arcos de custo negativo, a distância de s a t pode ser negativa.  Se t não está ao alcance de s, a distância de s a t não está definida (ou, se preferir, é infinita).

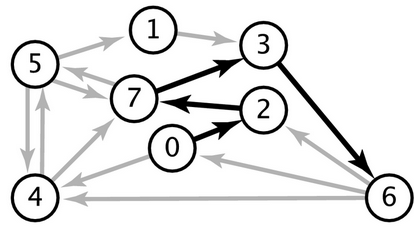
Exemplo A.  A tabela a seguir mostra um grafo com custos positivos nos arcos.  (O comprimento geométrico de cada arco na figura é proporcional ao seu custo.)

4-5 5-4 4-7 5-7 7-5 5-1 0-4 0-2 7-3 1-3 2-7 6-2 3-6 6-0 6-4
 35  35  37  28  28  32  38  26  39  29  34  40  52  58  93

Considere os caminhos que vão de 0 a 6.  O caminho  0-2-7-5-1-3-6  não tem custo mínimo pois o caminho  0-2-7-3-6  é mais barato.  O custo desse último caminho é 26+34+39+52 = 151.  Esse caminho é mínimo? A distância de 0 a 6 é 151?

    0   
   / \  
  1 — 2 

Exemplo B.  A tabela abaixo define um grafo com custos nos arcos. Considere os caminhos que começam no vértice 0.

0-1  0-2  2-0  1-2
 10    3    5  -20

O caminho  0-2  não é mínimo pois  0-1-2  é mais barato.  O caminho fechado  0-1-2-0  tem custo -5. Esse caminho é mínimo. Portanto, a distância de 0 a 0 é  -5.

Ciclos negativos

Num grafo com custos nos arcos, um ciclo é negativo se seu custo for negativo.  Se o grafo tem ciclos negativos, um caminho mínimo pode não ser simples.  Caso contrário, podemos supor que todo caminho mínimo é simples.

Para formular essa observação de maneira mais precisa, diremos que um ciclo C está ao alcance de um vértice s se algum vértice de C está ao alcance de s.  Temos então a seguinte

A expressão podemos supor sem perda de generalidade é uma referência à possível existência de ciclos de custo nulo pendurados no caminho. Esses ciclos não afetam o custo do caminho e portanto podem ser removidos do caminho.

A seguinte propriedade também decorre da ausência de ciclos negativos:

Graças a essas duas propriedades, o problema do caminho mínimo fica muito mais fácil quando restrito a grafos sem ciclos negativos.  Mas essa restrição levanta imediatamente a seguinte pergunta: como decidir se um grafo tem algum ciclo negativo?

Há dois casos em que a ausência de ciclos negativos é evidente: o caso em que todos os arcos têm custo positivo e o caso em que o grafo é acíclico.  Nos demais casos, não está claro como decidir se existe algum ciclo negativo. Trataremos dessa questão no capítulo Algoritmo de Bellman-Ford.

Exemplo C.  A tabela a seguir mostra um grafo com custos nos arcos.  O caminho 4-7-5-4 é um ciclo negativo. Seu custo é -1.

0-2 0-4 1-3 2-7 3-6 4-5 4-7 5-1 5-4 5-7 6-0 6-2 6-4 7-3 7-5
 26  38  29  34  52  35  37  32 -66  28  58  40  93  39  28

Potencial e condições de minimalidade

Para provar que um dado caminho C é mínimo, precisamos mostrar que todo caminho com a mesma origem e o mesmo término que os de C é pelo menos tão caro quanto C.  Para fazer isso, usaremos uma generalização do conceito de potencial relaxado introduzido no capítulo Caminhos de comprimento mínimo.

Um potencial é uma numeração dos vértices de G, ou seja, um vetor de números indexado pelos vértices de G.  Em relação a um potencial h[ ], dizemos que um arco v-w está tenso se  h[w] − h[v]  >  c,  está relaxado se  h[w] − h[v]  ≤  c  e  está justo se  h[w] − h[v]  ≡  c,  sendo c o custo do arco.  Em outras palavras, v-w está

• tenso se  h[v] + c  <  h[w] ,
• relaxado se  h[v] + c  ≥  h[w]  e
• justo se  h[v] + c  ≡  h[w] .

Um potencial é relaxado (ou viável) se todos os arcos de G estão relaxados em relação a ele.

Qualquer potencial relaxado h[ ] dá uma cota inferior para as distâncias entre vértices:  se P é um caminho de um vértice x a um vértice y então

cst(P)  ≥  h[y] − h[x],

sendo cst(P) o custo de P.  Por exemplo, se P é o caminho 0-1-2-3 e c_ij é o custo do arco i-j então  cst(P)  =  c₂₃ + c₁₂ + c₀₁  ≥  h[3] − h[2] + h[2] − h[1] + h[1] − h[0]  =  h[3] − h[0].  Em particular, se P for um ciclo então cst(P) ≥ 0.  Essas considerações levam à seguinte condição suficiente de minimalidade de um caminho:

Ao tratar dos caminhos que começam num certo vértice s, podemos nos limitar, sem qualquer prejuízo, ao sub­grafo induzido pelo conjunto de vértices que estão ao alcance de s.  Suporemos então, tacitamente, que

todos os vértices do nosso grafo estão ao alcance de s.

Isso tornará a discussão mais simples, evitando a constante repetição da frase para os vértices que estão ao alcance de s.   Adotada essa convenção simplificadora, podemos afirmar que vale então a seguinte recíproca limitada da condição suficiente:  Se o grafo não têm ciclos negativos então o vetor das distâncias a partir de s é um potencial relaxado.

Exemplo F.  Considere o grafo com custos nos arcos definido a seguir. Observe que todos os vértices estão ao alcance de 0 e que o grafo não tem ciclos negativos.

0-2 0-3 0-4 2-4 3-4 3-5 1-4 4-5 5-1 1-2
  7   2   8   1   7   1   1   0   3   3

A seguinte tabela dá um suposto vetor das distâncias a partir do vértice 0.

  v    0  1  2  3  4  5
d[v]   0  6  7  2  8  3 

O arco 1-4 não está relaxado em relação a d[]. Portanto, a tabela está errada.

Exemplo G.  Considere o grafo com custos nos arcos definido a seguir.  Observe que todos os vértices estão ao alcance de 0.

0-2 0-3 0-4 2-4 3-4 3-5 1-4 4-5 5-1 1-2
  7   2   8  -1   7   1  -1   0   3   3

Agora considere o potencial h[] definido pela tabela abaixo e verifique que o potencial é relaxado.

   v    0  1  2  3  4  5
 h[v]   0  6  7  2  5  3 

O caminho  0-3-5-1-4  tem custo 5. Como esse custo é igual à diferença h[4]-h[0], a condição suficiente de minimalidade garante que o caminho é mínimo.  (A propósito, a existência de um potencial relaxado mostra que o grafo não tem ciclos negativos. De fato, os dois únicos ciclos são 1-4-5-1 e 1-2-4-5-1 e ambos têm custo positivo.)

Árvore de caminhos baratos (CPT)

Para encontrar um caminho mínimo de um vértice s a um vértice t é inevitável calcular todos os caminhos mínimos que começam em s.  Isso sugere o seguinte conceito: uma árvore de caminhos baratos de um grafo G é uma subárvore radicada T de G tal que

1. todos os vértices do grafo estão em T  (ou seja, T é um sub­grafo gerador)  e
2. todo caminho em T que começa na raiz é mínimo em G.

Uma árvore de caminhos baratos também é conhecida pela abreviatura CPT de cheapest-paths tree.  (O conceito de árvore de caminhos baratos é uma generalização do conceito de árvore de caminhos curtos para grafos sem custos nos arcos.)

Um grafo tem uma CPT com raiz s se e somente se todos os vértices do grafo estão ao alcance de s e o grafo não tem ciclos negativos.  Esse fato decorre das duas propriedades enunciadas na seção Ciclos negativos acima.  Graças à convenção simplificadora adotada na seção anterior, podemos dizer que, em grafos sem ciclos negativos, o problema do caminho mínimo é equivalente ao seguinte

Uma árvore radicada T geradora de G é uma CPT de G se e somente se as distâncias em T a partir da raiz são um potencial relaxado em G.  Essa caracterização das soluções do problema da CPT decorre imediatamente das condições necessária e suficiente da seção anterior.  Essa caracterização é o primeiro passo na direção da solução do problema.

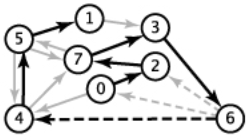
Exemplo D.  Considere o grafo com custos nos arcos definido a seguir.

0-2 0-4 1-3 2-7 3-6 4-5 4-7 5-1 5-4 5-7  6-0  6-2  6-4 7-3 7-5
 26  38  29  34  52  35  37  32  35  28 -140 -120 -125  39  28

A figura mostra uma sub­árvore radicada T com raiz 0. A seguinte tabela dá o vetor h[] das distâncias em T a partir de 0. 

  v    0   1   2   3   4   5   6   7  
h[v]   0  93  26  99  26  61 151  60

Verifique que h[] é um potencial relaxado no grafo. Portanto, T é uma CPT.  (A propósito, a existência de um potencial relaxado garante que o grafo não tem ciclos negativos.)

Algoritmos

Não se conhece um algoritmo rápido (mais precisamente, um algoritmo polinomial) para o problema do caminho de custo mínimo.  Entretanto, existem algoritmos razoávelmente rápidos para a restrição do problema a grafos que não têm ciclo negativo.  Em particular, existem algoritmos razoavelmente rápidos para o problema da CPT.  Todos calculam um vetor de pais pa[] e o correspondente vetor das distâncias dist[] aplicando a operação de relaxação

   if (dist[v] + cvw < dist[w]) {
       dist[w] = dist[v] + cvw;
       pa[w] = v;
   }

a cada arco v-w de custo cvw.  Quando todos os arcos estiverem relaxados, pa[] será o vetor de pais de uma CPT, conforme a condição suficiente da seção Potencial e condições de minimalidade acima.  Se for impossível relaxar todos os arcos, o algoritmo conclui que o grafo tem um ciclo negativo e portanto não tem CPT.

Os capítulos seguintes discutem três algoritmos para o problema da CPT:

• o algoritmo de Bellman-Ford,
• um algoritmo para dags, que se aplica apenas a grafos sem ciclos,
• o algoritmo de Dijkstra, que se aplica apenas a grafos sem arcos de custo negativo.