Algoritmos para Grafos, via Sedgewick  |  Índice remissivo

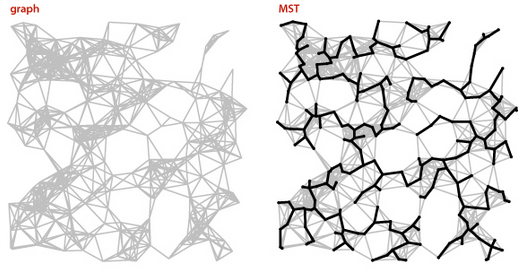
Árvores geradoras de custo mínimo

Esta página se aplica apenas a grafo: o problema aqui discutido não faz sentido em digrafos não simétricos.  (Há um problema semelhante em digrafos, mas ele é muito mais difícil.)

(Esta página é um resumo da introdução do capítulo 20 (Minimum Spanning Trees) e das seções 20.1 (Representations) e 20.2 (Underlying Principles of MST Algorithms), p.219-234, do livro de Sedgewick.)

Subgrafo de custo mínimo

Seja G um grafo com custos nas arestas (os custos podem ser positivos, negativos, ou nulos).  O custo de um subgrafo T de G é a soma dos custos das arestas de T.  Se U é uma coleção de subgrafos de G, um elemento T de U  tem custo mínimo  se o custo de T é menor ou igual [note o "ou igual"] que o custo de qualquer outro elemento de U.

Em outras palavras, T tem custo mínimo se nenhum elemento de U tem custo estritamente menor que o de T.

Árvore geradora mínima

Uma árvore geradora mínima (= minimum spanning tree), ou MST, de um grafo com custos nas arestas é qualquer árvore geradora do grafo que tenha custo mínimo.   Esta página estuda o seguinte:

Problema:  Encontrar uma MST de um grafo G com custos nas arestas.

É claro que o problema tem solução se e somente se o grafo G é conexo.   Boa pergunta:  como encontrar uma MST de um grafo conexo se todas as suas arestas têm o mesmo custo?

Exercícios

1. Encontre uma MST no grafo descrito a seguir (trata-se do grafo da figura 20.1, p.219, de Sedgewick):

        0-6  0-1  0-2  4-3  5-3  7-4  5-4  0-5  6-4  7-0  7-6  7-1
        .51  .32  .29  .34  .18  .46  .40  .60  .51  .31  .25  .21
   

2. Seja G um grafo conexo com custos nas arestas. Seja T uma MST de G.  Mostre que T continua sendo uma MST de G se o custo de cada aresta for multiplicado por um mesmo número c ≥ 0.  Mostre que T continua sendo uma MST de G se somarmos um mesmo número s (positivo ou negativo) ao custo de cada aresta. 
3. Suponha que os custos das arestas de um grafo conexo G são todos estritamente positivos.  Seja H um grafo de custo mínimo dentre todos os subgrafos conexos de G que contêm todos os vértices de G.  Mostre que H é uma MST de G.
4. Repita o exercício anterior sob uma hipótese mais fraca:  todo ciclo não trivial de G tem pelo menos uma aresta de custo estritamente positivo.
5. Suponha que os custos das arestas de um grafo são dois a dois distintos (ou seja, não há duas arestas com o mesmo custo). Mostre que o grafo tem uma única MST.
6. Considere a seguinte afirmação: Se um grafo tem uma única MST então os custos de suas arestas são distintos dois a dois.  Prove a afirmação ou dê um contraexemplo.
7. Considere o grafo cujos vértices são pontos no plano:

          vértices    0     1     2     3     4     5
       coordenadas  (1,3) (2,1) (6,5) (3,4) (3,7) (5,3)
   

   Suponha que as arestas do grafo são

   1-0 3-5 5-2 3-4 5-1 0-3 0-4 4-2 2-3
   

   e o custo de cada aresta v-w é igual ao comprimento do segmento de reta que liga os pontos v e w no plano.  Exiba uma MST desse grafo.

8. Como encontrar uma árvore geradora de custo máximo?

A propriedade dos ciclos

A Primeira Propriedade da Troca, discutida na página anterior, leva à seguinte condição de otimalidade:

Condição de Otimalidade:  Se T é uma MST de um grafo  então  toda aresta e fora de T tem custo máximo dentre as arestas do único ciclo não trivial em  T+e.

(A recíproca dessa proposição é verdadeira, mas sua demonstração é um pouco mais complexa.)

Exemplo:  Seja T a árvore geradora definida pelas 5 arestas "internas" da figura. Seja e a aresta "horizontal" "superior". Como e não é máxima no ciclo não trivial de T+e, a árvore T não é uma MST.

                              o-------2-------o
                              |\             /|
                              | 1           1 |
                              |  \         /  |
                              2   o---3---o   2
                              |  /         \  |
                              | 1           1 |
                              |/             \|
                              o-------4-------o

A propriedade dos cortes

A Segunda Propriedade da Troca, discutida na página anterior, leva à seguinte condição de otimalidade:

Condição de Otimalidade:  Se T é uma MST de um grafo  então  cada aresta t de T é uma aresta mínima dentre as que atravessam o corte determinado por T−t.

(A recíproca dessa proposição é verdadeira, mas sua demonstração é um pouco mais complexa.)

Exemplo:  Seja T a árvore geradora definida pelas cinco arestas "internas" da figura. Seja t a aresta "horizontal" no meio da figura. Como t não é mínima no corte determinado por T−t, a árvore T não é uma MST.

                              o-------2-------o
                              |\             /|
                              | 1           1 |
                              |  \         /  |
                              2   o---3---o   2
                              |  /         \  |
                              | 1           1 |
                              |/             \|
                              o-------4-------o

Exercícios

9. Seja C um ciclo não trivial em um grafo conexo G com custos nas arestas. Suponha que o custo de uma aresta e de C é estritamente maior que o custo de qualquer outra aresta de C.  É verdade que nenhuma MST de G contém e?
10. Seja G um grafo conexo com custos nas arestas. Suponha que o custo de uma aresta e de G é estritamente maior que o custo de qualquer outra aresta de G.  É verdade que nenhuma MST de G contém e?
11. Suponha que os custos das arestas de um grafo são distintos dois a dois. É verdade que a aresta de custo mínimo pertence à MST? 
12. Suponha que os custos das arestas de um grafo conexo são distintos dois a dois. É verdade que, em todo ciclo não trivial, a aresta de custo mínimo pertence à (única) MST do grafo? 
13. Seja T uma MST de um grafo G.  Suponha agora que uma das arestas de T é retirada de G.  Mostre como encontrar uma MST do novo grafo em tempo no pior caso proporcional ao número de arestas de G.
14. Seja T uma MST de um grafo com custos nas arestas. Suponha que um corte (X,Y) tem uma única aresta de custo mínimo. É verdade que T tem uma única aresta no corte?
15. Considere o grafo de um dos exercício acima. Encontre uma MST do grafo tomando as arestas na ordem dada e aplicando a propriedade dos ciclos repetidamente.
16. Mostre que o seguinte algoritmo produz uma MST:  Comece com árvore geradora T qualquer. Acrescente a T as demais arestas do grafo uma a uma. Para cada aresta acrescentada, retire de T uma aresta máxima do ciclo não trivial que se forma.
17. Mostre que o seguinte algoritmo produz uma MST:  Comece com árvore geradora T qualquer. Para cada aresta t de T, retire t de T e coloque em seu lugar uma aresta mínima do corte determinado por T−t.

Mais exercícios

18. Considere o seguinte grafo com custos nas arestas (trata-se do grafo da figura 20.1, p.219, de Sedgewick):

         0   1   2   3   4   5   6   7
    
    0    *  .32 .29  *   *  .60 .51 .31
    1   .32  *   *   *   *   *   *  .21
    2   .29  *   *   *   *   *   *   *
    3    *   *   *   *  .34 .18  *   *
    4    *   *   *  .34  *  .40 .51 .46
    5   .60  *   *  .18 .40  *   *   *
    6   .51  *   *   *  .51  *   *  .25
    7   .31 .21  *   *  .46  *  .25  * 
    

    Agora considere a árvore geradora

    0-2 4-3 5-3 7-4 7-0 7-6 7-1

    Para cada vértice v, escreva o vetor que dá o pai de cada vértice da árvore em relação à raiz v.

19. Suponha dada uma função GRAPHmstE que coloca num vetor mst as arestas de uma árvore.  Escreva uma função GRAPHmst que invoque GRAPHmstE e em seguida armazene num vetor parent o vetor de pais da árvore mst produzida por GRAPHmstE.