Main results and further information on the research area of numerical methods and computational geophysical fluid dynamics, mainly focused on the application on atmospheric modelling.
Selected Talks
Selected Scientific Results (up to 2021)
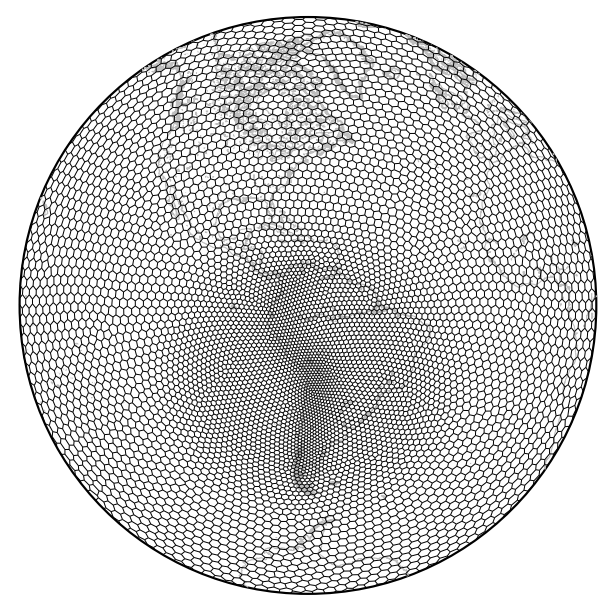
Topography based local spherical Voronoi grid refinement
This paper describes how to generate SCVT grids that are locally refined in South America and that also captures the sharp topography of the Andes Range by defining a density function based on topography and smoothing techniques. We investigate the use of the mimetic finite volume scheme employed in the MPAS dynamical core on this grid considering the non-linear classic and moist shallow-water equations on the sphere.
- Santos, L.F. and Peixoto, P.S., 2021. Topography based local spherical Voronoi grid refinement on classical and moist shallow-water finite volume models. Geoscientific Model Development, pp.1-31.
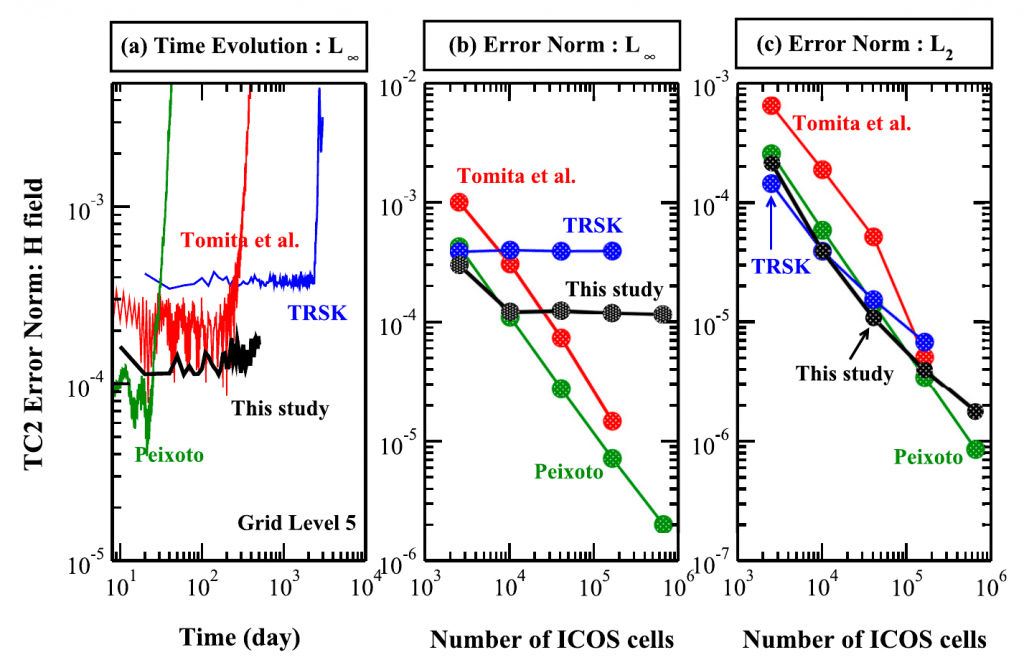
Comparing Numerical Accuracy of Icosahedral A-Grid and C-Grid Schemes in Solving the Shallow-Water Model
A collaborative study with NOAA-USA researchers comparing finite volume schemes currently used in two important models: MPAS (USA) and NICAM (Japan).
- Yu, Y.G., Wang, N., Middlecoff, J., Peixoto, P.S. and Govett, M.W., 2020. Comparing Numerical Accuracy of Icosahedral A-Grid and C-Grid Schemes in Solving the Shallow-Water Model. Monthly Weather Review, 148(10), pp.4009-4033.
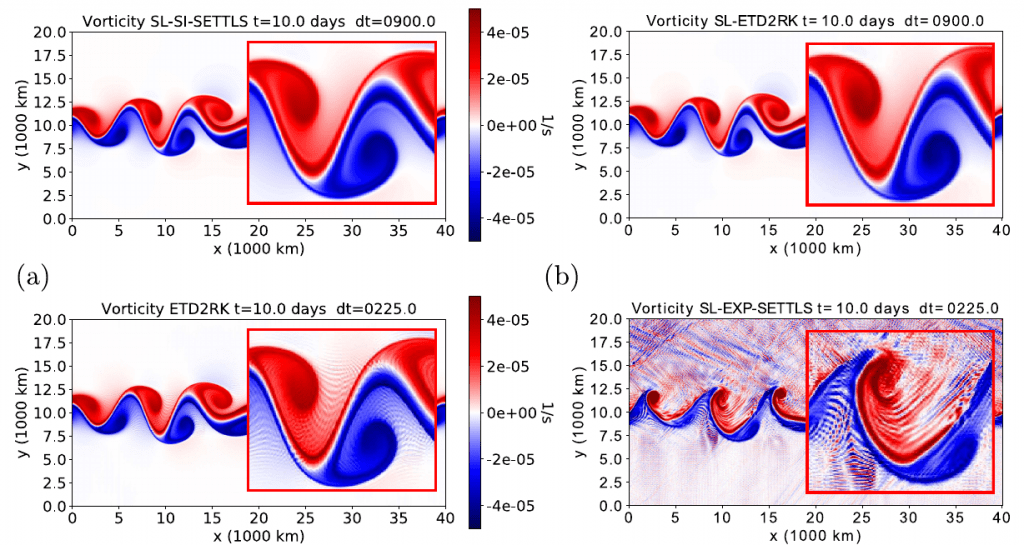
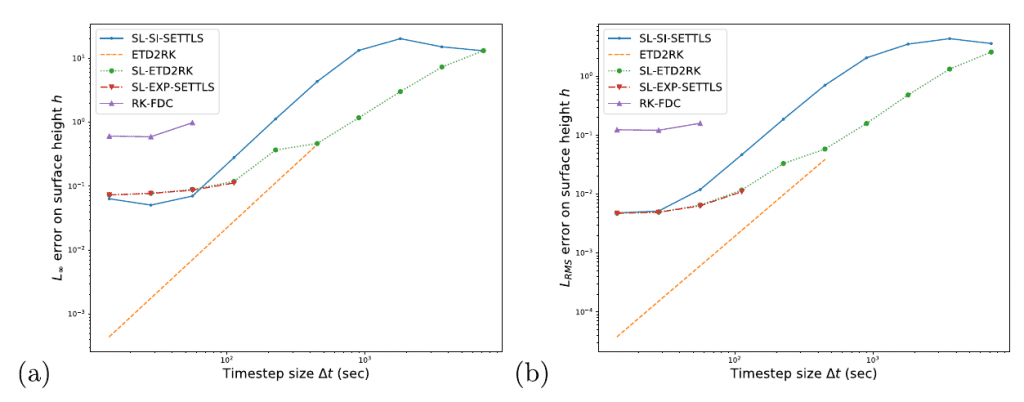
Semi-Lagrangian Exponential Integration with application to the rotating shallow water equations
In this paper, we propose a new class of numerical schemes formed from the fusion of two other classes of methods: Exponential integrators and semi-Lagrangian schemes. These new methods have the potential to allow larger time steps on equations with nonlinear advection with less impact on linear waves. Joint work with Martin Schreiber (TU Munich).
- Peixoto, P.S. and Schreiber, M., 2019. Semi-Lagrangian Exponential Integration with application to the rotating shallow water equations. SIAM Journal on Scientific Computing, 41(5), pp.B903-B928.
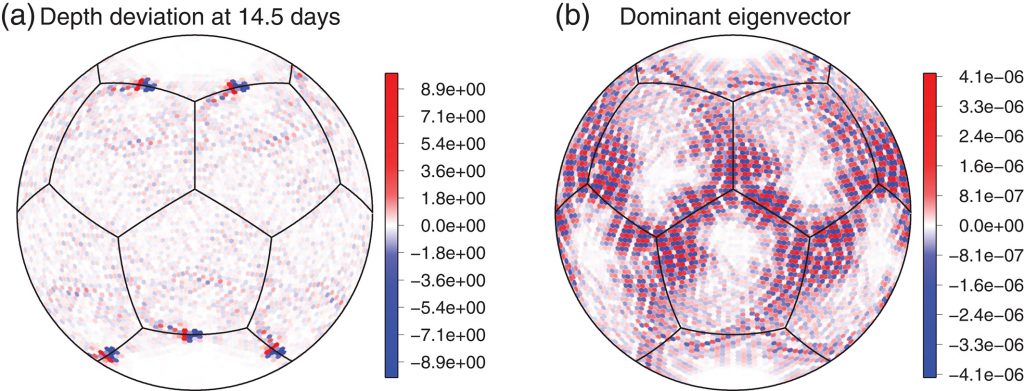
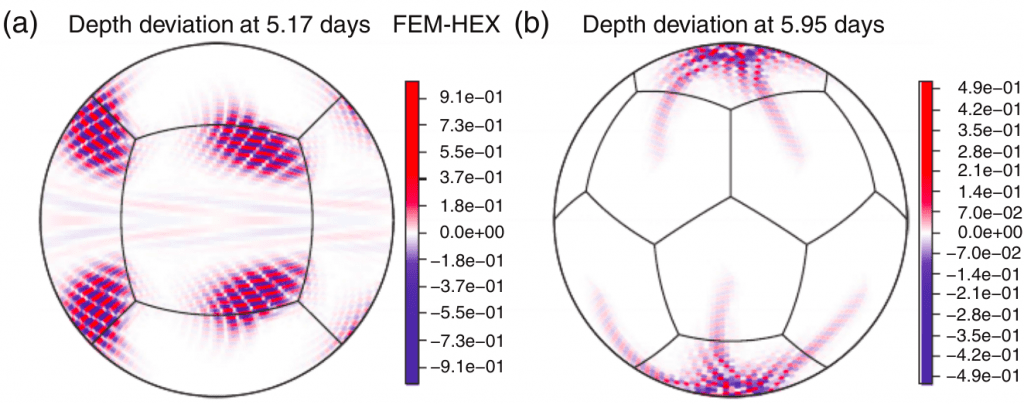
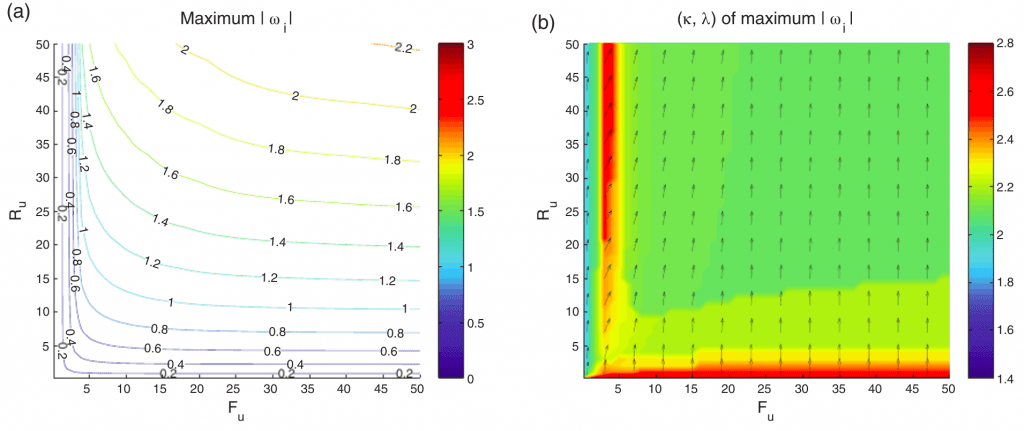
Numerical instabilities (Hollingsworth) on shallow water models with small equivalent depths
Research in collaboration with J. Thuburn (U. Exeter – UK) and M. Bell (UK MetOffice) about this intriguing numerical instability that has been affecting modern weather and climate models.
Peixoto, P.S., Thuburn, J. and Bell, M.J., 2018. Numerical instabilities of spherical shallow‐water models considering small equivalent depths. Quarterly Journal of the Royal Meteorological Society, 144(710), pp.156-171.
Bell, M.J., Peixoto, P.S. and Thuburn, J., 2017. Numerical instabilities of vector‐invariant momentum equations on rectangular C‐grids. Quarterly Journal of the Royal Meteorological Society, 143(702), pp.563-581.
Time parallelism in non-linear advection
Collaboration with researchers of TU Darmstadt (Germany) and Univ. de Exeter (UK) on the proposition of a parallel in time method with a semi-Lagrangian coarse solver.
Schmitt, A., Schreiber, M., Peixoto, P. and Schäfer, M., 2018. A numerical study of a semi-Lagrangian Parareal method applied to the viscous Burgers equation. Computing and Visualization in Science, 19(1-2), pp.45-57.
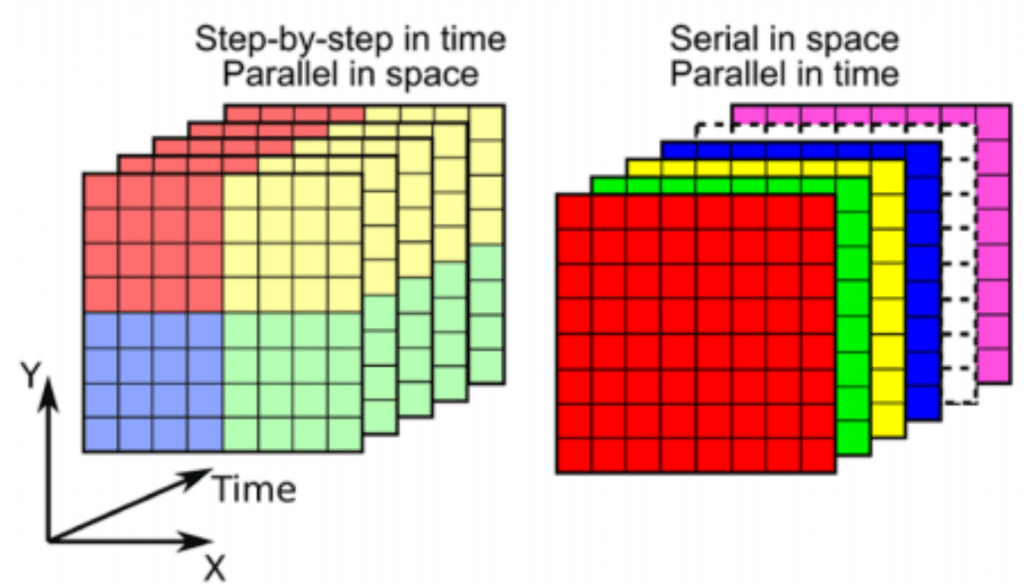
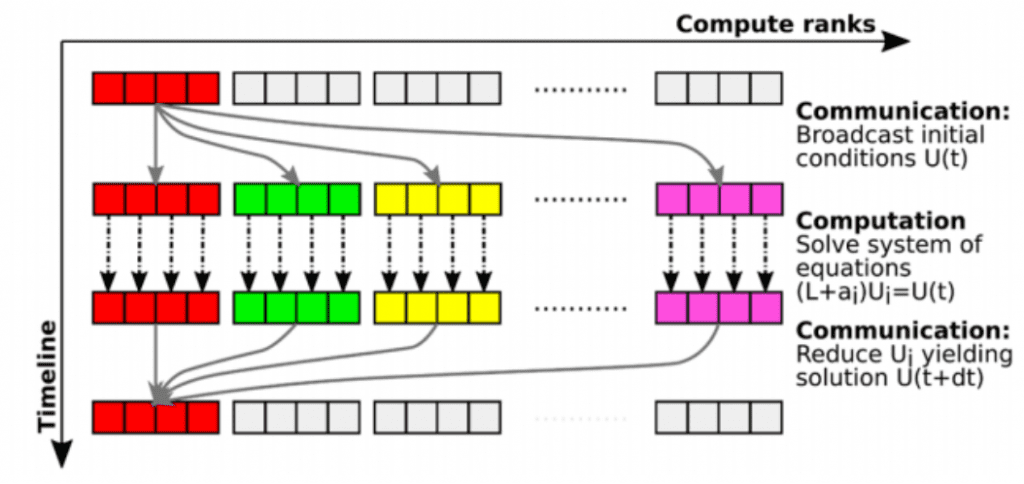
Massively parallel exponential integrator
Research in collaboration with researchers of the University of Exeter (UK) and Los Alamos Nat. Lab (USA) aiming to solve PDEs with linear oscillatory operators with a highly parallel exponential integration technique.
Schreiber, M., Peixoto, P.S., Haut, T. and Wingate, B., 2018. Beyond spatial scalability limitations with a massively parallel method for linear oscillatory problems. The International Journal of High Performance Computing Applications, 32(6), pp.913-933.
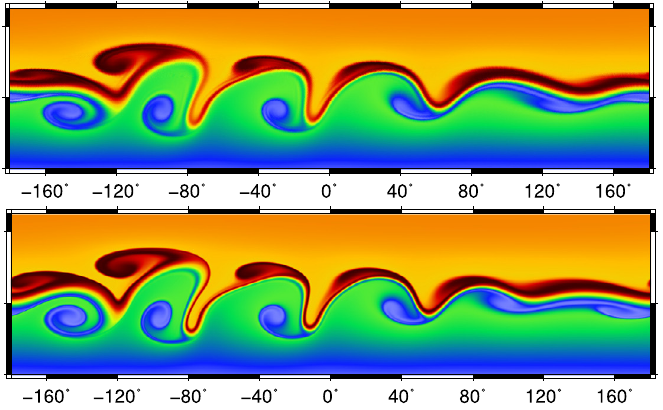
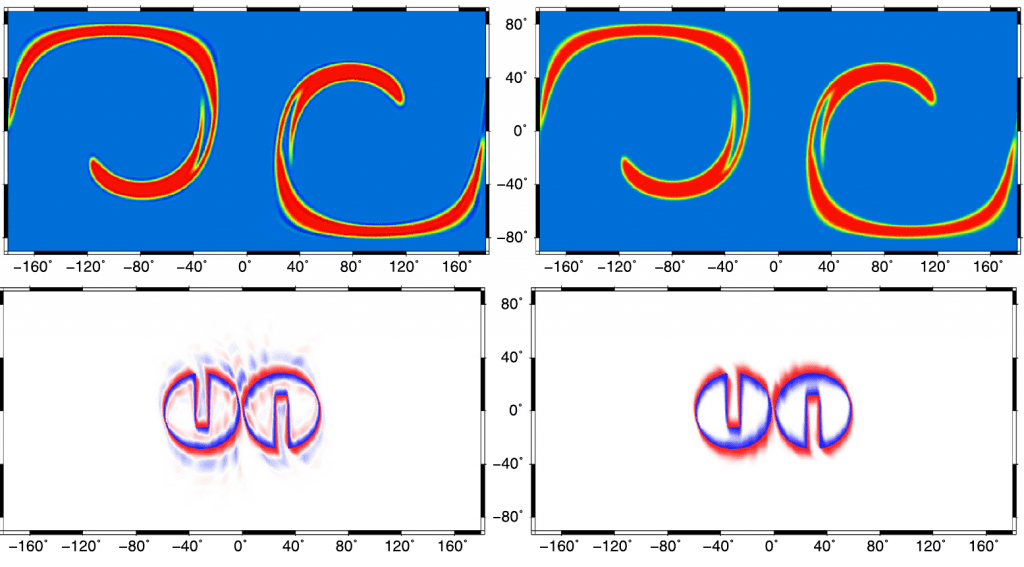
Accuracy analysis of mimetic finite volume operators on geodesic grids
Investigation on accuracy issues of finite volume schemes used in modern weather and climate models.
Peixoto, P.S., 2016. Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative. Journal of Computational Physics, 310, pp.127-160.
Vector reconstructions on geodesic grids
A review and proposal of vector reconstruction schemes on geodesic grids and aiming to semi-Lagrangian transport schemes on the sphere.
Peixoto, P.S. and Barros, S.R., 2014. On vector field reconstructions for semi-Lagrangian transport methods on geodesic staggered grids. Journal of Computational Physics, 273, pp.185-211.
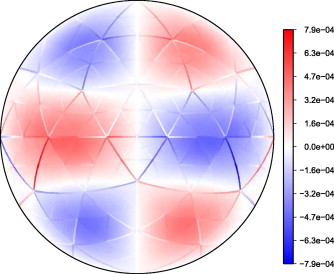
Grid imprinting on geodesic grids
A theoretical result that explains the appearance of grid imprinting on finite volume schemes on icosahedral spherical grids.
Peixoto, P.S. and Barros, S.R., 2013. Analysis of grid imprinting on geodesic spherical icosahedral grids. Journal of Computational Physics, 237, pp.61-78.
Wavelets and PDEs
The proposition of a wavelet-based spectral scheme for 1D PDEs and an application to a precipitation (rain) model.
Barros, S.R. and Peixoto, P.S., 2011. Computational aspects of harmonic wavelet Galerkin methods and an application to a precipitation front propagation model. Computers & Mathematics with Applications, 61(4), pp.1217-1227.