Capítulo 5 Semana 5

5.1 Aula 20

Variáveis aleatórias discretas são frequentemente classificadas de acordo com suas funções de probabilidade. A seguir, apresentamos alguns dos tipos mais comuns.

Variáveis aleatórias Bernoulli e Binomial

Suponha que um experimento cujo resultado possa ser classificado como sucesso ou fracasso seja realizado. Se $X=1$ quando o resultado é sucesso e $X=0$ quando fracasso, então, a função de probabilidade de $X$ é dada por \[\begin{align} p(0) &= P(\{X=0\}) = 1-p,\\ p(1) &= P(\{X=1\}) = p, \tag{5.1} \end{align}\] em que $p$, $0\leq p \leq 1$, é a probabilidade de que a tentativa seja um sucesso. Uma variável aleatória $X$ é chamada de variável aleatória de Bernoulli se sua função de probabilidade for dada como na Expressão (5.1), para $p \in (0,1)$. Notação: $X \sim \mathrm{Bernoulli}(p)$.

Suponha agora que $n$ tentativas independentes, cada uma com probabilidade $p$ de sucesso e probabilidade de fracasso $1-p$, sejam realizadas. Se $Y$ representa o número de sucessos que ocorrem nas $n$ tentativas, enão $Y$ é uma variável aleatória binomial com parâmetros $(n,p)$. Note que uma variável aleatória Bernoulli é uma variável aleatória binomial com parâmetros $(1,p)$. Notação: $X \sim \mathrm{bin}(n,p)$.

A função de probabilidade de uma variável aleatória binomial com parâmetros $(n,p)$ é \[p(i) = \underbrace{n \choose i}_{\substack{\small{\text{De $n$ repetições}} \\ \small{\text{do experimento, em quantas}} \\ \small{\text{combinações aparecem}} \\ \small{\text{$y$ sucessos}}}} \times \underbrace{p^i}_{\substack{\small{\text{Probabilidade}}\\ \small{\text{de sucesso}} \\ \small{\text{ocorrendo $y$ vezes}}}} \times \underbrace{(1-p)^{n-1}}_{\substack{\small{\text{Probabilidade de fracasso}} \\ \small{\text{ocorrendo $(n-y)$ vezes}}}},\] para $i=0,1,2,\ldots,n$.

Observação. Teorema binomial: \[(x+y)^n = \sum_{k=0}^{n}{n \choose k}x^ky^{n-k}.\]

Pelo teorema binomial, a soma das probabilidades é igual a $1$ \[\sum_{i=0}^{\infty}p(i) = \sum_{i=0}^{n}{n \choose i}p^i(1-p)^{n-i} = [p+(1-p)]^n=1.\]

Exemplo 5.1 Cinco moedas honestas são lançadas. Se os resultados por hipótese são independentes, determine a função de probabilidade do número de caras obtido.

Solução. Se $X$ é o número de caras (sucessos) obtidas, então $X\sim \mathrm{bin}(n=5, p=1/2)$. Então \[\begin{align} P(X=0) &= {5 \choose 0} \bigg(\frac{1}{2}\bigg)^0 \bigg(\frac{1}{2}\bigg)^5 = \frac{1}{32},\\ P(X=1) &= {5 \choose 1} \bigg(\frac{1}{2}\bigg)^1 \bigg(\frac{1}{2}\bigg)^4 = \frac{5}{32},\\ P(X=2) &= {5 \choose 2} \bigg(\frac{1}{2}\bigg)^2 \bigg(\frac{1}{2}\bigg)^3 = \frac{10}{32},\\ P(X=3) &= {5 \choose 3} \bigg(\frac{1}{2}\bigg)^3 \bigg(\frac{1}{2}\bigg)^2 = \frac{10}{32},\\ P(X=4) &= {5 \choose 4} \bigg(\frac{1}{2}\bigg)^4 \bigg(\frac{1}{2}\bigg)^1 = \frac{5}{32},\\ P(X=5) &= {5 \choose 5} \bigg(\frac{1}{2}\bigg)^5 \bigg(\frac{1}{2}\bigg)^0 = \frac{1}{32}. \end{align}\]

Exemplo 5.2 Os parafusos produzidos em certa empresa tem probabilidade $0{,}01$ de apresentar defeitos, independentemente uns dos outros. A empresa vende os parafusos em pacotes com $10$ unidades e oferece uma garantia se mais de 1 parafuso apresentar defeito. Que proporção de pacotes vendidos a empresa deve trocar?

Solução. Defina $X=$ “número de parafusos defeituosos em um pacote”. Note que $X \sim \mathrm{bin}(10, 0{,}01)$. Então, temos que calcular \[\begin{align} P(X > 1) &= 1 - \big[P(X=0)+P(X=1)\big] \\ &= 1 - P(X=0)-P(X=1)\\ &= 1 - {10 \choose 0}(0{,}01)^0(0{,}99)^10-{10 \choose 1}(0{,}01)^1(0{,}99)^9\\ &= 0{,}004. \end{align}\]

Propriedades das variáveis aleatórias binomiais

Para começar, vamos calcular o seu valor esperado e sua variância. Então, \[\begin{align*} E[X^k] &= \sum_{i=0}^{n}i^k{n \choose i}p^i(1-p)^{n-1}\\ &=\sum_{i=1}^{n}i^k{n \choose i}p^i(1-p)^{n-1}. \end{align*}\]

Usando a identidade \[i{n \choose i} = n{n-1 \choose i-1},\] temos \[\begin{align*} E[X^k] &= np\sum_{i=0}^{n}i^{k-1}{n-1 \choose i-1}p^{i-1}(1-p)^{n-i}\\ &\stackrel{\text{j=i-1}}{=} np\sum_{j=0}^{n}(j+1)^{k-1}{n-1 \choose j}p^{j}(1-p)^{n-1-j}\\ &=npE[(Y+1)^{k-1}], \end{align*}\] em que $Y$ é uma variável aleatória binomial com parâmetros $n - 1,$ $p$. Fazendo $k = 1$ na equação anterior, temos \[E[Y] = np.\]

Fazendo $k = 2$ na equação anterior e usando a fórmula precedente para o valor esperado de uma variável aleatória binomial, temos \[\begin{align*} E[X^2] &= np(1-p)E[Y+1] \\ &= np[(n-1)p+1]. \end{align*}\] Como $E[X] = np$, obtemos \[\begin{align*} Var(X) &= E[X^2] - E[X]^2\\ &= np[(n-1)p+1] - (np)^2\\ &= np(1-p). \end{align*}\]

Exemplo 5.3 Seja $X$ uma variável aleatória binomial com parâmetros $n = 6$, $p = 0{,}4$. Calcular $P(X=i)$, $i=0,1,\ldots,6.$

Solução. Vamos utilizar a linguagem R para realizar os calculos através da função dbinom.

dbinom(0, 6, 0.4) # P(X=0)

## [1] 0.046656

dbinom(1, 6, 0.4) # P(X=1)

## [1] 0.186624

dbinom(2, 6, 0.4) # P(X=2)

## [1] 0.31104

dbinom(3, 6, 0.4) # P(X=3)

## [1] 0.27648

dbinom(4, 6, 0.4) # P(X=4)

## [1] 0.13824

dbinom(5, 6, 0.4) # P(X=5)

## [1] 0.036864

dbinom(6, 6, 0.4) # P(X=6)

## [1] 0.004096

Como R é uma linguagem de programação vetorizada, podemos fazer todos os cálculos utilizando apenas o comando abaixo.

dbinom(0:6, 6, 0.4)

## [1] 0.046656 0.186624 0.311040 0.276480 0.138240 0.036864 0.004096

Além da função dbinom, existem outras funções implementadas em R que são relacionadas à distribuição binomial, a saber

dbinom calcula a densidade, por exemplo, para obter $P(a<X<b)$, use sum(dbinom(a:b, 6, 0.4)),
pbinom calcula a função de distribuição, por exemplo, para obter $P(X\leq a)$, use pbinom(a, 6, 0.4),
qbinom obtem o quantil, por exemplo, para obter $x$ tal que $P(X<x)=a$, use qbinom(a, 6, .4),
rbinom gera uma amostra aleatória de X, por exemplo, para obter $n$ observações use rbinom.

Exemplo 5.4 A probabilidade de um determinado perfil de cliente adquirir uma apólice de seguro é $0{,}20$. Suponha que os clientes comportem-se de maneira independente.

Se um corretor visitar 3 clientes, com esse determinado perfil, qual a probabilidade de exatamente 2 negócios serem fechados? ($Y$)
Qual a distribuição de probabilidades de $Y$?
Se ele visita 100 clientes, qual a probabilidade de fechar exatamente 20 negócios?
Se um corretor visita 100 clientes, qual a probabilidade de fechar no máximo 20 negócios?
Se um corretor visita 100 clientes, qual a probabilidade de fechar pelo menos 20 negócios
Qual é o valor esperado de negócios fechados ao visitar 100 clientes?

Solução. Note que neste experimento há 3 ensaios de Bernoulli em que o sucesso é o “cliente adquire o seguro”. A probabilidade $p$ do sucesso é $0,20$. Considere então $Y=$ “número de clientes que adquirem o seguro quando se abordam 3 clientes”. Claramente, $Y\sim\mathrm{Binomial}(3; 0{,}20).$

Assim, (a) $P(Y=2) =$ ${3 \choose 2}(0{,}2)^2(1-0{,}2)^{3-2}$ = dbinom(2, 3, 0.2) = $0{,}096$.

Como mencionado anteriormente, (b) a variável aleatória $Y$ segue uma distribuição binomial com parâmetros $n=3$ e $p=0{,}2$.

Agora, vamos considerar $Z=$ “número de clientes que adquirem o seguro quando se abordam 100 clientes”. A probabilidade de adquirir o seguro continua sendo $p=0{,}2$ e $Z\sim\mathrm{Binomial}(100; 0{,}20).$ Então, (c) $P(Z=20) =$ ${100 \choose 20}(0{,}2)^{20}(1-0{,}2)^{100-20}$ = dbinom(20, 100, 0.2) = $0{,}096.$

Fechar no máximo 20 contratos é o evento $Z \leq 20$, então (d) $P(Z\leq 20) =$ $\sum_{i=0}^{20}{100 \choose i}(0{,}2)^{i}(1-0{,}2)^{100-i}$ = sum(dbinom(0:20, 100, 0.2)) = $0{,}559.$

Fechar pelo menos 20 contratos é o evento $Z \geq 20$, então (e) $P(Z> 19) =$ $\sum_{i=20}^{100}{100 \choose i}(0{,}2)^{i}(1-0{,}2)^{100-i}=$ $1-P(Z<19)=$ 1-sum(dbinom(0:19, 100, 0.2)) = $0{,}540.$

Como $Z\sim\mathrm{Binomial}(100; 0{,}20),$ temos que (f) $E[Z] = np = 20.$

Agora, vamos calcular as probabilidades $P(Y=i)$, para $i=0, 1, 2, 3,$ e $P(Z=j)$, para $j=0, \ldots, 100,$ e construir um gráfico com os resultados, veja o código abaixo e a Figura 5.1.

n <- 3
p <- 0.2
df_bin3 <- data.frame(x = 0:n,
                 prob = dbinom(x = 0:n, size = n, prob = p))

n <- 100
df_bin100 <- data.frame(x = 0:n,
                 prob = dbinom(x = 0:n, size = n, prob = p))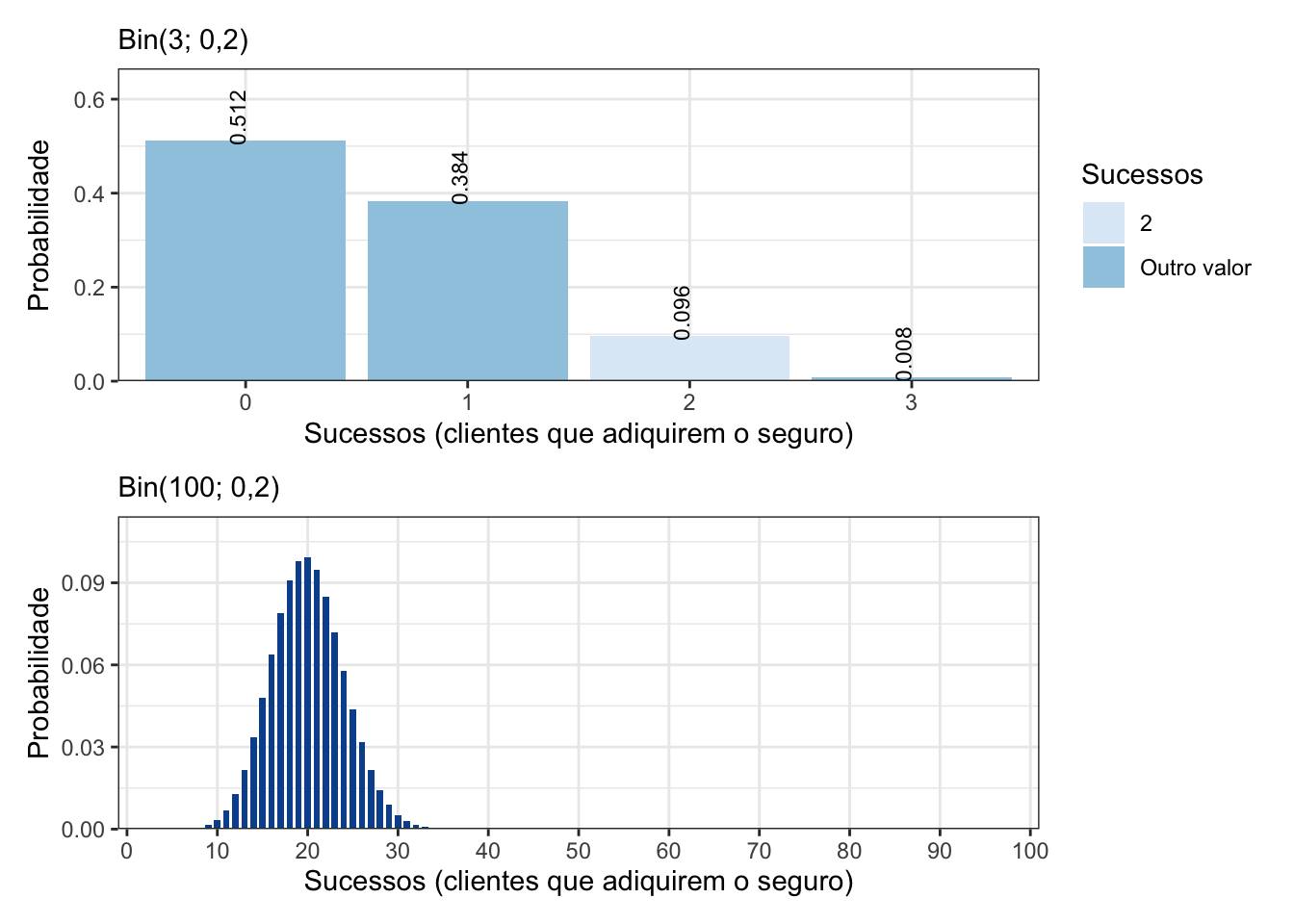

Figura 5.1: Probabilidade do número sucessos de uma variável aleatória Bin(3; 0,2) e Bin(100; 0,2).

5.2 Aula 21

Variável aleatória geométrica

Suponha que tentativas independentes, cada uma delas com probabilidade de sucesso $p$, $0<p<1$, sejam realizadas até que ocorra um sucesso. Seja $X$ o número de tentativas necessárias. Então \[\begin{equation} P(X=n) = (1-p)^{n-1}p, \qquad n=1,2,\ldots \tag{5.2} \end{equation}\] Note que, para que $X$ seja igual a $n$ é necessário e suficiente que as $n-1$ primeiras tentantivas sejam fracassos e que a $n$-ésima tentativa seja um sucesso. Como supomos independência entre os resultados das tentativas sucessivas, obtemos a Equação (5.2). Dizemos que qualquer variável aleatória $X$ com função de probabilidade dada pela Equação (5.2) é uma variável aleatória geométrica com parâmetro $p$. Notação: $X\sim\mathrm{Geométrica}(p).$

Propriedades da variável aleatória geométrica

Os resultados a seguir não serão provados, pois sua prova foge do escopo deste curso. Se $X\sim\mathrm{Geométrica}(p)$, então \[E[X] = \frac{1}{p},\] e \[\mathrm{Var}(X) = \frac{1-p}{p^2}.\]

Exemplo 5.5 Um casal com problemas para engravidar, recorreu a uma técnica de inseminação artificial no intuito de conseguir o primeiro filho ou filha. A eficiência da referida técnica é de $0{,}20$ e o custo de cada inseminação R$ $2000{,}00$.

Qual a probabilidade de que o casal obtenha êxito na terceira tentativa?
Qual o custo esperado deste casal para obter o primeiro filho?

Solução. Note que $X\sim\mathrm{Geométrica}(p=0{,}2).$

$P(X=3) =$ $(1-p)^2 p^1 =$ $(1-0{,}2)^2 0{,}2=$ $0{,}128$.
$E[X] = \frac{1}{p} = \frac{1}{0{,}2} = 5.$ Como cada procedimento custa R$ $2000{,}00$, o custo esperado para obter o primeiro filho ou a primeira filha será de R$ $5\cdot 2000{,}00$ = R$ $10.000{,}00.$

Para fazer cálculos com a distribuição geométrica na linguagem R, utilize as funções dgeom, pgeom, qgeom e rgeom. Por exemplo, se $X\sim\mathrm{Geométrica}(0{,}2)$, para obter $P(X=3)$ use dgeom(3-1, 0.2). Note que o primeiro argumento não é número de tentativas, mas sim o número de fracassos, ou seja, $n-1.$

Agora, vamos calcular as probabilidades $P(X=i)$, para $i=0, \ldots, 20,$ e construir um gráfico com os resultados, veja o código abaixo e a Figura 5.2.

n <- 20
p <- 0.2
df <- data.frame(x = 0:n, 
                 prob = dgeom(x = 0:n, prob = p))

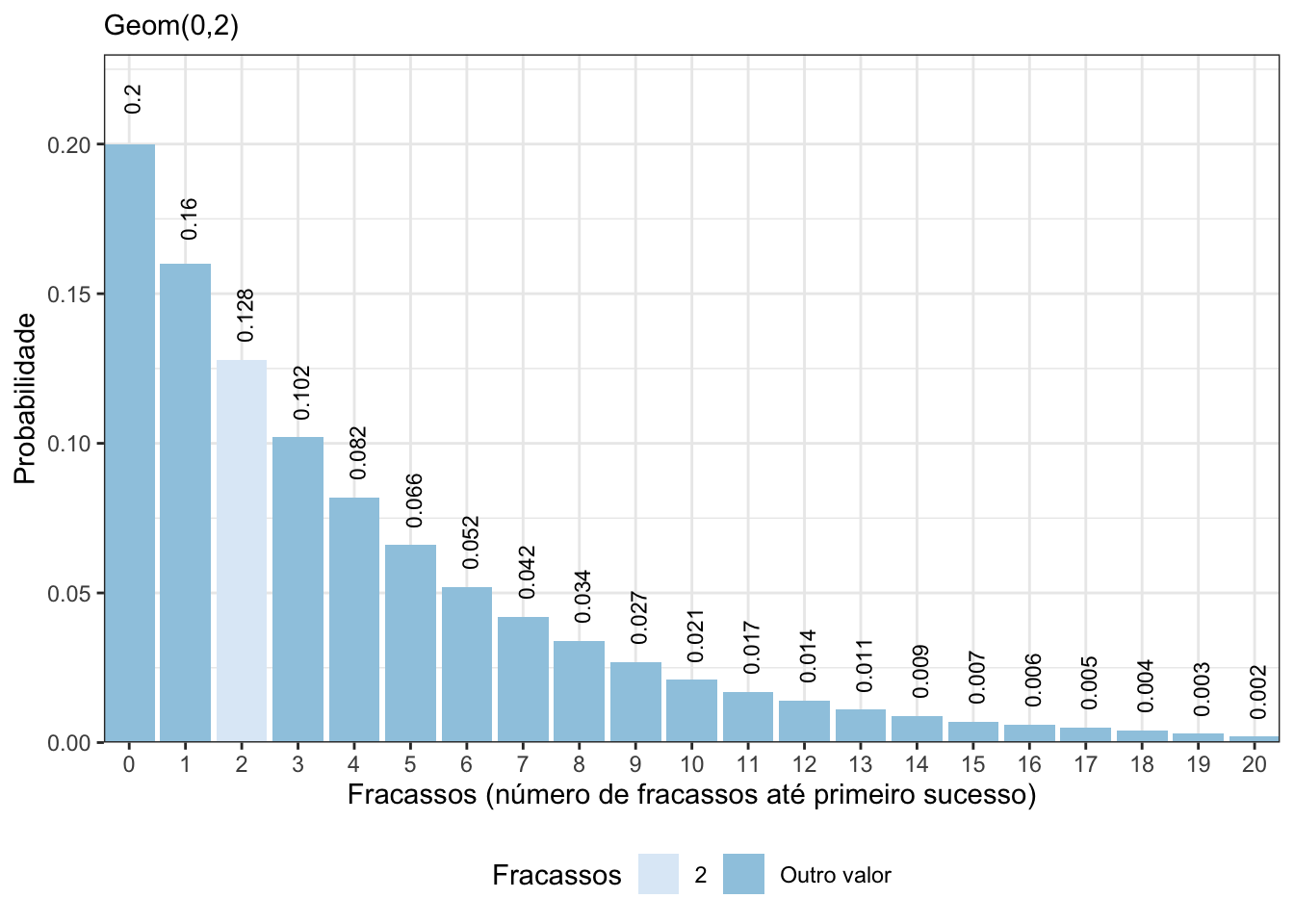
Figura 5.2: Distribuição de probabilidade de uma variável aleatória Geom(0,2) e Bin(100; 0,2).

Variável aleatória binomial negativa

Suponha que tentativas independentes com mesma probabilidade de sucesso $p$, $0<p<1$, sejam realizadas até que se acumule um total de $r$ sucessos. Seja $X$ o número de tentativas necessárias, então \[\begin{equation} P(X=n) = {n-1 \choose r-1}p^r(1-p)^{n-r}, \qquad n=r,r+1,\ldots \tag{5.3} \end{equation}\] Note que, para que o $r$-ésimo sucesso ocorra na $n$-ésima tentantiva, devem ocorrer $r-1$ sucessos nas primeiras $n-1$ tentativas e na $n$-ésima tentativa deve ser um sucesso. A probabilidade do primeiro evento é \[{n-1 \choose r-1}p^{r-1}(1-p)^{n-r}\] e a probabilidade do segundo é $p$. Pela independência entre as tentativas, obtemos a Equação (5.3). Dizemos que qualquer variável aleatória $X$ com função de probabilidade dada pela Equação (5.3) é uma variável aleatória binomial negativa com parâmetros $(r,p)$. Notação: $X\sim\mathrm{BN}(r,p).$

Observação. Uma variável aleatória geométrica é simplesmente uma variável binomial negativa com parâmetros $(1; p)$.

Propriedades da variável aleatória binomial negativa

Se $X\sim\mathrm{BN}(r; p)$, então \[E[X] = \frac{r}{p},\] e \[\mathrm{Var}(X) = \frac{r(1-p)}{p^2}.\]

Exemplo 5.6 Uma petroleira realiza um estudo geológico que indica que em uma área de exploração de petróleo uma perfuração para construção de um poço deve ter 25% de chance de encontrar petróleo.

Qual é a probabilidade de que a primeira obtenção de petróleo aconteça no terceiro poço perfurado?
Qual é a probabilidade de que a terceira vez que obtêm-se petróleo aconteça na sétima tentativa?
Qual é a média e a variância do número de poços que devem ser furados se a companhia petroleira deseja ter três poços extraindo petróleo?

Solução.

Para obter a probabilidade requerida, temos que encontrar $P(X=3)$, em que $X\sim\mathrm{Geométrica}(p=0{,}25)$, pois estamos considerando apenas um único sucesso. Então, \[P(X=3) = (1-0{,}25)^2(0,25) = 0{,}141.\]
Agora, temos que considerar a variável aleatória $Y$ que representa o número de tentativas até obter 3 sucessos e encontrar $P(Y=7)$. Note que $Y\sim\mathrm{BN}(r=3,p=0{,}25).$ Então $P(Y=7) =$ ${6\choose 2}0{,}25^3(1-0{,}25)^4 =$ $0{,}074.$

Utilizando a linguagem R, podemos encontrar as respostas usando (a) dgeom(3-1, 0.25) e (b) dnbinom(7-3,size=3,prob=0.25). Note que para a binomial negativa, devemos informar o número de fracassos $n-r$ ao invés do número de tentativas $n$.

Temos que \[E[X] = \frac{r}{p} = \frac{3}{0{,}25} = 12,\] e \[\mathrm{Var}(X) = \frac{r(1-p)}{p^2} = \frac{3(1-0{,}25)}{0{,}25^2} = 36.\]

Agora, vamos calcular as probabilidades $P(X=i)$, para $i=3, \ldots, 10$ e construir um gráfico com os resultados, veja o código abaixo e a Figura 5.3.

r <- 3
p <- 0.25
df <- data.frame(x = 0:25, 
                 prob = dnbinom(x = 0:25, size = r, prob = p))

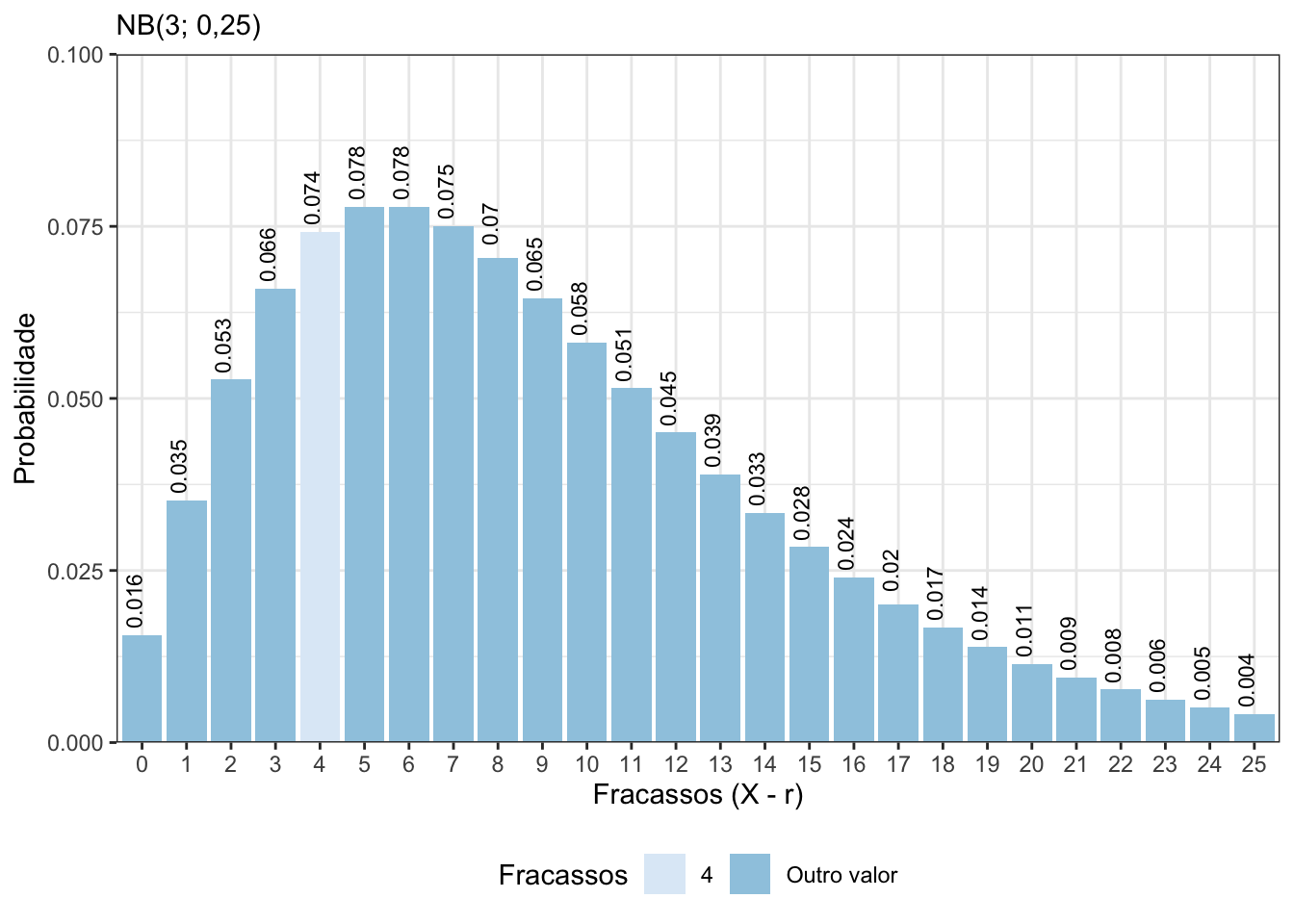
Figura 5.3: Probabilidade do número de tentativas até obter 3 sucessos de uma variável aleatória BN(3; 0,25).

5.3 Aula 22

Variável aleatória Poisson

A variável aleatória de Poisson encontra uma ampla faixa de aplicações em diversas áreas, tais como

Número de novos casos de coronavírus ao longo de um dia;
Número de usuários conectados no Facebook em um minuto;
Número de acidentes em 100 km de uma rodovia;
Número de clientes na fila em um minuto (teoria das filas);
Consumo de um produto em um mês (gestão de estoques).

Algumas suposições que são feitas a respeito dessa distribuição são

Probabilidade de uma ocorrência é a mesma para dois intervalos quaisquer de igual tamanho;
A ocorrência ou não num dado intervalo é independente da ocorrência ou não em outro intervalo.

Seja $X$ o número de ocorrências de um evento num intervalo de tempo ou espaço, então dizemos que $X\sim\mathrm{Poisson}(\lambda)$ e \[\begin{equation} p(i) = P(X=k) = e^{-\lambda}\frac{\lambda^k}{k!}, \qquad k=0,1,2,\ldots \tag{5.4} \end{equation}\]

A Equação (5.4) define uma função de probabilidade já que $\sum_{k=0}^{\infty}P(X=k)=$ $e^{-\lambda} \sum_{k=0}^{\infty}\frac{\lambda^k}{k!}=$ $e^{-\lambda}e^{\lambda}=$ $1$.

Propriedades da variável aleatória Poisson

Se $X\sim\mathrm{Poisson}(\lambda)$, então \[E[X] = \mathrm{Var}(X) = \lambda.\]

Exemplo 5.7 Uma fábrica produz 24 horas por dia. Interrupções na linha de montagem por falha humana ocorrem a uma taxa média de 4 a cada 24 horas.

Qual é a probabilidade de ocorrerem exatamente 3 interrupções em um dia de trabalho?
Qual é a probabilidade de ocorrem exatamente 3 interrupções em 2 dias de trabalho?

Solução. Note que $X\sim\mathrm{Poisson}(\lambda=4).$

$P(X = 3) =$ $e^{-4}\frac{4^3}{3!} =$ $0{,}1954.$
Agora, considere $Y\sim\mathrm{Poisson}(\lambda=8)$. Então, $P(Y=3) =$ $e^{-8}\frac{8^3}{3!} =$ $0{,}0286.$

Para obter esses valores usando o R, utilize (a) dpois(x=3,lambda=4) e (b) dpois(3,8).

Vamos considerar a variável aleatória $X$ definida no Exemplo 5.7, calcular $P(X=x)$, para $x=0,1,\ldots, 15$ e fazer um gráfico com essas probabilidades. Veja o código abaixo e a Figura 5.4.

lambda <- 4
df <- data.frame(x = 0:15, 
                 prob = dpois(x = 0:15, lambda = lambda))

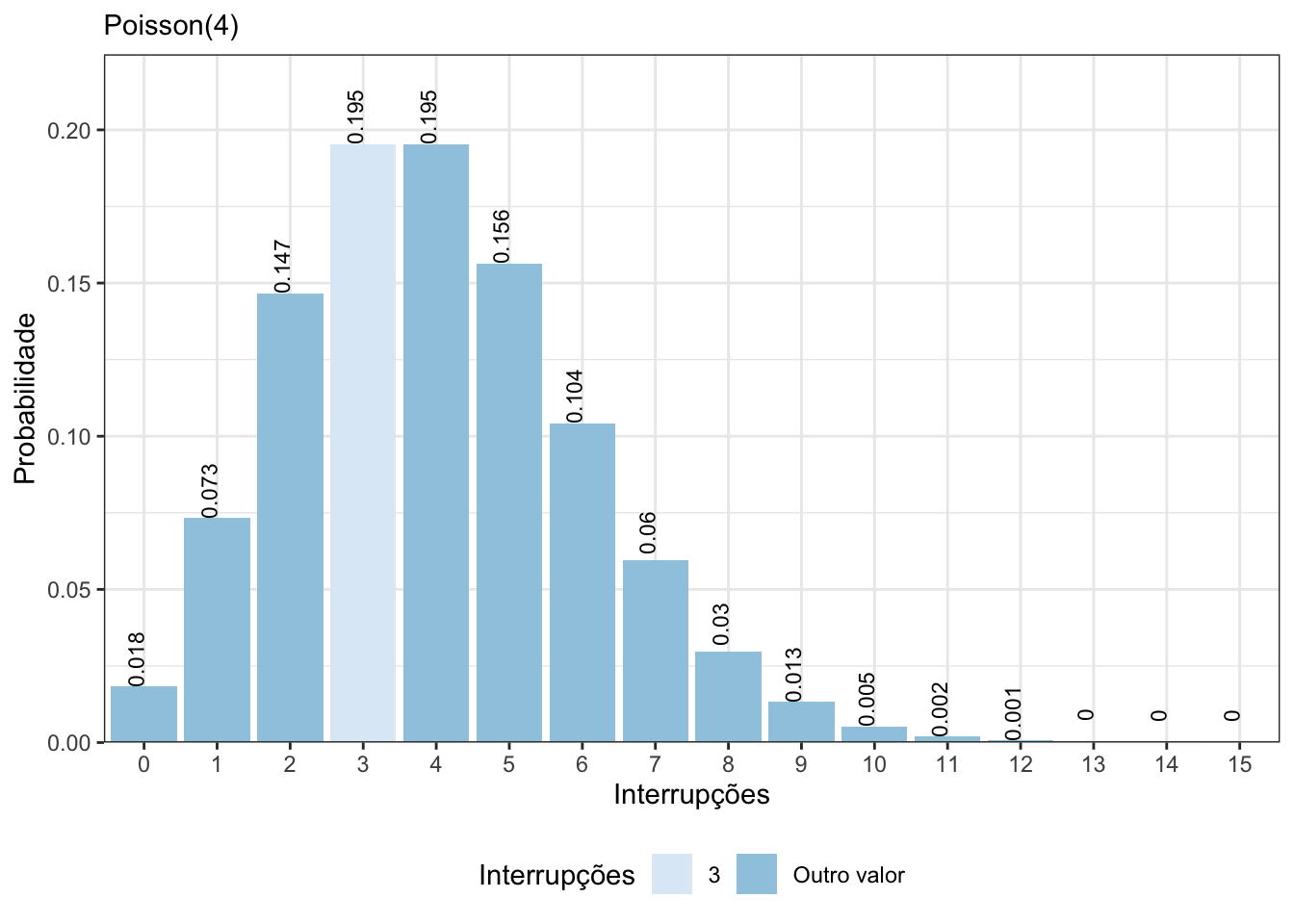
Figura 5.4: Gráfico de probabilidade de uma Poisson(4).

Valor esperado da soma de variáveis aleatórias

Para uma variável aleatória $X$, suponha que $X(s)$ represente o valor de $X$ quando $s \in S$ é o resultado do experimento. Agora, se $X$ e $Y$ são ambas variáveis aleatórias, então sua soma também o é. Isto é, $Z = X + Y$ também é uma variável aleatória. Além disso, $Z(s) = X(s) + Y(s)$.

Exemplo 5.8 Considere o experimento de jogar uma moeda 5 vezes, sendo o resultado a sequência obtida de caras e coroas. Suponha que $X$ seja o número de caras que saem nas primeiras 3 jogadas e $Y$ o número de caras que saem nas 2 últimas jogadas. Seja $Z = X + Y$. Então, por exemplo, para o resultado $s = (h, t, h, t, h)$ em que $h$ é cara e $t$ é coroa, \[\begin{align*} X(s) &= 2,\\ Y(s) &= 1,\\ Z(s) &= X(s) + Y(s) = 3 \end{align*}\] o que significa que o resultado $(h, t, h, t, h)$ resulta em 2 caras nas primeiras três jogadas, 1 cara nas últimas duas jogadas, e em um total de 3 caras nas cinco jogadas.

Seja $p(s) = P(\{s\})$ a probabilidade de que $s$ seja o resultado do experimento. Como podemos escrever qualquer evento $A$ como a união finita ou contavelmente infinita dos eventos mutuamente exclusivos $\{s\},s \in A$, tem-se pelos axiomas da probabilidade que \[P(A) = \sum_{s \in A}p(s).\] Quando $A=S,$ temos que $P(A) = \sum_{s \in A}p(s) = 1.$

Proposição 5.1 \[E[X]=\sum_{s\in\mathcal{S}}X(s)p(s).\]

Prova. Suponha que os valores distintos de $X$ sejam $x_i$, $i\geq 1$. Para cada $i$, suponha que $S_i$ seja o evento em que $X$ é igual a $x_i$. Isto é, $S_i=\{s:X(s)=x_i\}$. Então \[\begin{align*} E[X] &= \sum_i x_iP(X=x_i)\\ &= \sum_i x_iP(S_i)\\ &= \sum_i x_i \sum_{s\in\mathcal{S_i}} p(s)\\ &= \sum_i \sum_{s\in\mathcal{S_i}} x_ip(s)\\ &= \sum_i \sum_{s\in\mathcal{S_i}} X(s)p(s)\\ &= \sum_{s\in\mathcal{S}} X(s)p(s) \end{align*}\] em que obtemos a igualdade final porque $S_1, S_2, \ldots,$ são eventos mutualmente exclusivos cuja união é $\mathcal{S}.$

Exemplo 5.9 Suponha que duas jogadas independentes de uma moeda que dá cara com probabilidade $p$ sejam feitas, e suponha que $X$ represente o número obtido de caras. Como \[\begin{align*} P(X=0) &= P(t,t) = (1-p)^2, \\ P(X=1) &= P(h,t) + P(t,h) = 2p(1-p),\\ P(X=2) &= P(h,h) = p^2, \end{align*}\] temos que, pela definição de valor esperado, \[E[X]=0\cdot (1-p)^2 + 1\cdot 2p(1-p) + 2\cdot p^2 = 2p,\] que é idêntico à \[\begin{align*} E[X] &= X(h,h)p^2 + X(h,t)p(1-p) + X(t,h)(1-p)p + X(t,t)(1-p)^2\\ &= 2p^2 + p(1-p) + (1-p)p\\ &= 2p. \end{align*}\]

Corolário 5.1 Para as variáveis aleatórias $X_1, X_2, \ldots, X_n$, \[E\bigg[\sum_{i=1}^{n}X_i\bigg] = \sum_{i=1}^{n}E[X_i].\]

Prova. Seja $Z = \sum_{i=1}^{n}X_i$. Então, pela Proposição 5.1, \[\begin{align*} E[Z] &= \sum_{s\in\mathcal{S}}Z(z)p(s)\\ &= \sum_{s\in\mathcal{S}}\big(X_1(s)+X_2(s)+\cdots+X_n(s)\big)p(s)\\ &= \sum_{s\in\mathcal{S}}X_1(s)p(s) + \sum_{s\in\mathcal{S}}X_2(s)p(s) + \cdots + \sum_{s\in\mathcal{S}}X_n(s)p(s)\\ &= E[X_1] + E[X_2] + \cdots + E[X_n]. \end{align*}\]

Exemplo 5.10 Determine o número esperado de sucessos que resultam de $n$ tentativas quando a tentativa $i$ tem probabilidade de sucesso $p_i$, $i = 1,\ldots, n$.

Solução. Fazendo \[\begin{equation*} X_1 = \begin{cases} 1 & \text{se a tentativa $i$ é um sucesso}\\ 0 & \text{se a tentativa $i$ é um fracasso,} \end{cases} \end{equation*}\] temos a representação \[X=\sum_{i=1}^{n}X_i.\] Consequentemente, \[E[X] = \sum_{i=1}^{n}E[X_i] = \sum_{i=1}^{n}p_i\]

5.4 Aula 23

Propriedades da função de distribuição acumulada

Lembre-se da Definição 4.4. A função distribuição $F(x)$ de $X$ representa a probabilidade de que a variável aleatóriia $X$ assuma um valor menor ou igual a $x$. Abaixo, apresentamos algumas propriedades da função de distribuição acumulada $F$:

$F$ é uma função não decrescente, isto é, se $a<b$ então $F(a)<F(b).$
$\lim_{b\rightarrow \infty}F(b) = 1;$
$\lim_{b\rightarrow -\infty}F(b) = 0;$
$F$ é contínua à direita, isto é, para qualquer $b$ e qualquer sequência decresccente $b_n$, $n\geq 1,$ que convirja para $b$, $\lim_{b\rightarrow \infty}F(b_n) = F(b).$

Obtém-se a Propriedade 1 porque, para $a<b$, o evento $\{X<a\}$ está contido no evento $\{X<b\}$ e portanto não pode ter uma probabilidade maior. As propriedades 2, 3 e 4 resultam da propriedade da continuidade de probabilidades. Por exemplo, para provar a Propriedade 2, observamos que se $b_n$, tende a $\infty$, então os eventos $\{X<b_n\}$, $n \geq 1$, são eventos crescentes cuja união é o evento $\{X<\infty\}.$ Portanto, pela propriedade da continuidade de probabilidades, \[\lim_{n\rightarrow \infty}P(X\leq X_n) = P(X<\infty) = 1,\] o que prova a Propriedade 2. A prova da Propriedade 3 é similar e por isso será deixada como exercício.

Para provar a Propriedade 4, observamos que se $b_n$ decresce em direção a $b$, então $\{X\leq b_n\}$, $n\geq 1,$ são eventos decrescentes cuja interseção é $\{X\leq b\}.$ A propriedade da continuidade então determina que \[\lim_{n}P(X\leq b_n) = P(X\leq b),\] o que verifica a Propriedade 4.

Podemos usar $F(x)$ para obter $P(a < X \leq b),$ \[P(a < X \leq b) = F(b) - F(a),\] para todo $a<b.$

Funções conjuntamente distribuídas

Frequentemente estamos interessados em analisar a probabilidade de duas ou mais variáveis aleatórias simultaneamente.

Definição 5.1 (função de probabilidade conjunta) Para quaisquer duas variáveis aleatórias discretas $X$ e $Y$, \[p(x; y) = P(X=x; Y=y) = P(\{X=x\} \cap \{Y=y\}).\]

A função de probabilidade de $X$ pode ser obtida de de $p(x,y)$ por \[p_X(x) = P(X=x) = \sum_{y:p(x,y)>0}p(x,y),\] similarmente \[p_Y(y) = P(Y=y) = \sum_{x:p(x,y)>0}p(x,y).\] As distribuições $p_X$ e $p_Y$ são chamadas de distribuições marginais.

5.5 Aula 24

Exemplo 5.11 Suponha que 3 bolas sejam sorteadas de uma urna contendo 3 bolas vermelhas, 4 bolas brancas e 5 bolas azuis. Se $X$ e $Y$ representam, respectivamente, o número de bolas vermelhas e brancas escolhidas, determine a função de probabilidade conjunta de $X$ e $Y$.

Solução. A função de probabilidade conjunta de $X$ e $Y$, $p(i,j)=P(X=i,Y=j)$ é dada por \[\begin{align} p(0,0) &= \frac{{3\choose 0}{4\choose 0}{5\choose 3}}{{12 \choose 3}}, &\qquad p(1,0) &= \frac{{3\choose 1}{4\choose 0}{5\choose 2}}{{12 \choose 3}},\\ p(0,1) &= \frac{{3\choose 0}{4\choose 1}{5\choose 2}}{{12 \choose 3}}, &\qquad p(1,1) &= \frac{{3\choose 1}{4\choose 1}{5\choose 1}}{{12 \choose 3}},\\ p(0,2) &= \frac{{3\choose 0}{4\choose 2}{5\choose 2}}{{12 \choose 3}}, &\qquad p(1,2) &= \frac{{3\choose 1}{4\choose 2}{5\choose 0}}{{12 \choose 3}},\\ p(0,3) &= \frac{{3\choose 0}{4\choose 3}{5\choose 0}}{{12 \choose 3}}, &\qquad p(1,3) &= 0,\\ p(2,0) &= \frac{{3\choose 2}{4\choose 0}{5\choose 1}}{{12 \choose 3}}, &\qquad p(2,1) &= \frac{{3\choose 2}{4\choose 1}{5\choose 0}}{{12 \choose 3}},\\ p(3,0) &= \frac{{3\choose 3}{4\choose 0}{5\choose 0}}{{12 \choose 3}}. \end{align}\]

Estas probabilidades pode ser apresentadas em forma de tabela, veja na Tabela 5.1.

Tabela 5.1: Distribuição conjunta de X e Y.
	P(Y=0)	P(Y=1)	P(Y=2)	P(Y=3)	P(X=j)
P(X=0)	0,0455	0,1818	0,1364	0,0182	0,3818
P(X=1)	0,1364	0,2727	0,0818	0,0000	0,4909
P(X=2)	0,0682	0,0545	0,0000	0,0000	0,1227
P(X=3)	0,0045	0,0000	0,0000	0,0000	0,0045
P(Y=i)	0,2545	0,5091	0,2182	0,0182	1,0000

5.6 Variáveis aleatórias independentes

As variáveis aleatórias $X$ e $Y$ são independentes se, para quaisquer dois conjuntos de números reais $A$ e $B$ \[\begin{equation} P(X\in A, Y\in B) = P(X\in A)P(Y\in B). \tag{5.5} \end{equation}\] Em outras palavras, $X$ e $Y$ são independentes se, para todo $A$ e $B$, os eventos ${X\in A}$ e ${Y\in B}$ forem independentes.

Usando os três axiomas da probabilidade, pode-se provar que a Equação (5.5) é obtida se, e somente se, para todo $a$ e $b$, \[P(X\leq a, Y\leq b) = P(X\leq a)P(Y\leq b).\] Portanto, em termos da função distribuição conjunta $F$ de $X$ e $Y$ são independentes se \[F(a,b)=F_X(a)F_Y(b).\] para todo $a$ e $b$.

Se $X$ e $Y$ são variáveis aleatórias discretas, a condição de independência (5.5) é equivalente a \[\begin{equation} p(x,y) = p(x)p(y) \tag{5.6} \end{equation}\] para todo $x$ e $y$. Essa equivalência existe porque, se a Equação (5.5) é satisfeita, então obtemos a Equação (5.6) fazendo com que $A$ e $B$ sejam, respectivamente, os conjuntos unitários $A=\{x\}$ e $B=\{y\}$. Além disso, se a Equação (5.5) é válida, então, para quaisquer conjuntos $A$ e $B$, \[\begin{align*} P(X\leq a, Y\leq b) &= \sum_{y\in B}\sum_{x\in A}p(x,y)\\ &= \sum_{y\in B}\sum_{x\in A}p_X(x)p_Y(y)\\ &= \sum_{y\in B}p_Y(y)\sum_{x\in A}p_X(x)\\ &=P(X\in B)P(X \in A) \end{align*}\] e a Equação (5.6) é estabelecida.

Exemplo 5.12 No Exemplo 5.11, as variáveis aleatórias $X$ e $Y$ são independentes?

Solução. As variáveis aleatórias serão independentes se a igualdade $P(X=i,Y=j)=P(X=i)P(X=j)$ valer para todo $i$ e $j$. Note que, se $i=0$ e $j=0$, \[0{,}0455=P(X=0,Y=0)\neq P(X=i)P(X=j)=0{,}0972.\] Portanto $X$ e $Y$ não são independentes.

5.7 Soma de variáveis aleatórias independentes

É muitas vezes importante poder calcular a distribuição de $X + Y$ a partir das distribuições de $X$ e $Y$ quando $X$ e $Y$ são independentes. Sejam $X$ e $Y$ variáveis aleatórias discretas e considere a variável aleatória $X+Y.$ Note que o evento $\{X + Y = n\}$ pode ser escrito como a união dos eventos disjuntos $\{X=k, Y=n-k\}$, $O\leq k \leq n$. A função distribuição de $X+Y$ é obtida da seguinte maneira \[\begin{align*} P(X+Y=n) &=\sum_{k=0}^{n}P(X=k,y=n-k)\\ &=\sum_{k=0}^{n}P(X=k)P(y=n-k). \end{align*}\]

No próximo exemplo vamos obter a distribuição da soma de variáveis aleatórias de Poisson independentes.

Exemplo 5.13 Se $X$ e $Y$ são variáveis aleatórias de Poisson independentes com respectivos parâmetros $\lambda_1$ e $\lambda_2$, calcule a distribuição de $X + Y$.

Solução. Lembre que, como mencionado anteriormente, o evento $\{X + Y = n\}$ pode ser escrito como a união dos eventos disjuntos $\{X=k, Y=n-k\}$, $0\leq k \leq n$. Então,

\[\begin{align*} P(X+Y=n) &=\sum_{k=0}^{n}P(X=k,y=n-k)\\ &=\sum_{k=0}^{n}P(X=k)P(y=n-k)\\ &=\sum_{k=0}^{n}\frac{e^{-\lambda_1}\lambda_1^k}{k!}\frac{e^{-\lambda_2}\lambda_2^{n-k}}{(n-k)!}\\ &=e^{-(\lambda_1+\lambda_2)}\sum_{i=1}^{n}\frac{\lambda_1^k\lambda_2^{n-k}}{k!(n-k)!}\\ &=\frac{e^{-(\lambda_1+\lambda_2)}}{n!}(\lambda_1+\lambda_2)^n. \end{align*}\] Assim, $X+Y$ segue uma distribuição de Poisson com parâmetros $\lambda_1+\lambda_2$.

5.8 Distribuições condicionais

Se $X$ e $Y$ são variáveis aleatórias discretas, é natural definir a função discreta de probabilidade de $X$ dado que $Y=y$ como \[\begin{align*} p_{X|Y}(x|y) &= P(X=x|Y=y)\\ &=\frac{P(X=x|Y=y)}{P(Y=y)}\\ &=\frac{p(x,y)}{p_Y(y)}. \end{align*}\] para todos os valores de $y$ tais que $p_Y(y)>0.$ Similarmente, a função distribuição de probabilidade $X|Y=y$ é definida, para todo $y$ tal que $p_Y(y)>0,$ como \[\begin{align*} F_{X|Y}(x|y) &= P(X\leq x|Y=y)\\ &=\sum_{a\leq x}p_{X|Y}(a,y). \end{align*}\] Se $X$ é independente de $Y$, então a função de probabilidade condicional e a função distribuição são iguais aos respectivos casos incondicionais.

Exemplo 5.14 Voltando ao Exemplo 5.11, calcule a função de probabilidade condicial de $X$ dado que $Y=2.$

Solução. Primeiro, note que \[\begin{align*} p_Y(2) = \sum_x p(x, 2) = 0{,}2182. \end{align*}\] Assim, \[\begin{align*} p_{X|Y}(0,2) = \frac{p(0,2)}{p_{Y}(2)} = 0{,}6251,&\qquad p_{X|Y}(1,2) = \frac{p(1,2)}{p_{Y}(2)} = 0{,}3749,\\ p_{X|Y}(2,2) = \frac{p(2,2)}{p_{Y}(2)} = 0, &\qquad p_{X|Y}(3,2) = \frac{p(3,2)}{p_{Y}(2)} = 0.\\ \end{align*}\]

Exemplo 5.15 Voltando ao Exemplo 5.11, calcule $E[X|Y=2]$ e $\mathrm{Var}(X|Y=2).$

Solução. Com os resultados do Exemplo 5.14, temos que \[\begin{align*} E[X|Y=2] &= \sum_x xp(x|y)\\ &= 0\cdot 0{,}6251+ 1\cdot 0{,}3749 + 2\cdot 0 + 3\cdot 0\\ &= 0{,}3749. \end{align*}\]

E também, \[\begin{align*} \mathrm{Var}(X|Y=2) &= \sum_x (y-E[X|Y=y])^2p(x|y) \\ &= 0{,}2343. \end{align*}\]