Capítulo 3 Semana 3

3.1 Aula 11

3.1.1 Mais exemplos com permutações

Exemplo 3.1 Determine o número de permutações simples dos elementos \(a_1, a_2, \ldots, a_n\) nas quais \(a_1\) está em primeiro ou \(a_2\) está em segundo lugar.

Solução. Seja \(A_1\) o conjunto das permutações em que \(a_1\) está em primeiro lugar e \(A_2\) o conjunto das permutações em que \(a_2\) está em segundo lugar. É claro que \(|A_1|=|A_2|=(n-1)!\) e \(|A_1 \cap A_2| = (n-2)!\). Logo, o número que procuramos é \(|A_1\cup A_2|\),

\[\begin{align} |A_1\cup A_2| &= |A_1| + |A_2| - |A_1 \cap A_2| \\ &= (n-1)! + (n-1)! - (n-2)!\\ &= 2(n-1)! - (n-2)!\\ &= 2(n-1)(n-2)! - (n-2)!\\ &= (2n - 2-1)(n-2)!\\ &= (2n-3)(n-2)!.\\ \end{align}\]

Definição 3.1 (Permutação Caótica) Uma permutação de \(a_1, a_2, \ldots, a_n\) é chamada de caótica quanto nenhum dos \(a_i\)´s se encontra na posição original, isto é, na \(i\)-ésima posição.

Seja \(A_i=\) “o conjunto das permutações de \(a_1, a_2, \ldots, a_n\) tendo \(a_i\) no \(i\)-ésimo lugar”. Para calcular o número de permutações caóticas, denotado por \(D_n\) (desarranjo), devemos calcular o número de elementos que não pertencem a nenhum dos \(A_i\)´s:

\[D_n = \Bigg|\overline{\bigcup_{i=1}^{n} A_i} \Bigg| = \Bigg|{\bigcap_{i=1}^{n} \overline{A_i}}\Bigg|.\]

Veja que \[\begin{align} |A_i| &= (n-1)! &\qquad \text{existem $n$ termos iguais a este na soma}\\ |A_i\cap A_j| &= (n-2)! &\qquad \text{existem $C_n^1$ termos iguais a este na soma}\\ |A_i\cap A_j \cap A_k| &= (n-3)! &\qquad \text{existem $C_n^2$ termos iguais a este na soma}\\ &\vdots \\ |A_1\cap\cdots\cap A_n| &= 1 &\qquad \text{existem $C_n^n$ termos iguais a este na soma}.\\ \end{align}\] Então,

\[\begin{align} D_n = \Bigg|{\bigcap_{i=1}^{n} \overline{A_i}}\Bigg| &= n! - n(n-1)! + C_n^2(n-2)! - C_n^3(n-3)! + \cdots + (-1)^n\cdot 1 \\ &= n! - \frac{n!}{1} + \frac{n!}{2!(n-2)!}(n-2)! - \frac{n!}{3!(n-3)!}(n-3)! + \cdots + (-1)^n\frac{n!}{n!}\\ &= n! - \frac{n!}{1} + \frac{n!}{2!} - \frac{n!}{3!} + \cdots + (-1)^n\frac{n!}{n!}\\ &= n! \Bigg(1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots +(-1)^n\frac{1}{n!}\Bigg). \end{align}\]

Exemplo 3.2 Quantas permutações dos inteiros \(1,2,3,\ldots,10\) tem exatamente \(4\) dos números em suas posições originais?

Solução. Como não são fixados os \(4\) números que permanecerão nas suas posições originais, devemos escolher esstes números. Essa escolha pode ser feita de \(C_{10}^4\) maneiras distintas. Em seguinda, devemos permutar os \(6\) números restantes caoticamente. Então, a resposta será \[C_{10}^4 D_6 = \frac{10!}{4!6!} 6! \Bigg(1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \frac{1}{4!} - \frac{1}{5!} + \frac{1}{6!}\Bigg) = 55650.\]

3.1.2 Contando o número de funções

Teorema 3.1 Sejam \(A\) e \(B\) conjuntos, em que \(|A|=n\) e \(|B|=k\). Se \(k=n\), \(n>0\), então o número de funções bijetoras \(f:A\rightarrow B\) é \(k!\).

Prova. Se em \(A\) existem \(n\) pontos \(a_1, \ldots, a_n\), temos \(n\) possíveis imagens para \(a_1\), \(n-1\) possíveis imagens para \(a_2\), \(n-2\) para \(a_3\), \(\ldots\), 1 para \(a_n\).

Teorema 3.2 Sejam \(A\) e \(B\) conjuntos, em que \(|A|=n\) e \(|B|=k\). Se \(n\leq k\), então o número de funções injetoras \(f:A\rightarrow B\) é \(k(k-1)(k-2)\cdots(k-n-1)!\).

Prova. Exercício!

Proposição 3.1 Se \(|A|=m\) e \(|B|=n\), então o número de funções \(f:A\rightarrow B\) é \(n^m\)

Prova. (por indução) Para \(m=0\), temos que \(|A|=0\) e a única função é a função vazia. Neste caso, \(n^0=1\). Suponha que vale para \(m\) e assuma \(|A|=m+1\). Seja \(a \in A\) (qualquer) e seja \(|A^\prime|=A\setminus\{a\}\), um conjunto tal que \(|A^\prime|=m\). Qualquer função \(f:A\rightarrow B\) atribui um elemento \(f(a)\in B\) para \(a\) e \(f|_{A^\prime}\) sendo uma função de \(A^\prime\) à \(B\). Pela hipótese de indução, existem \(n^m\) funções de \(A^\prime\) à \(B\). Logo, existem \(n\) maneiras de atribuir \(f(a)\in B\) para \(a \in B\), logo, pelo Princípio Multiplicativo, existem \[n\cdot n^m = n^{m+1}\] funções de \(A\) à \(B\).

Na contagem do número de aplicações sobrejetoras é que necessitamos do princípio de inclusão e exclusão.

Teorema 3.3 Sejam \(A\) e \(B\) conjuntos, em que \(|A|=n\) e \(|B|=k\). Para \(n\geq k\), o número de funções sobrejetoras \(f:A\rightarrow B\) é dado por \[T(n,k) = \sum_{i=0}^{k}(-1)^i{k \choose i}(k-i)^n.\]

Prova. Como sabemos, uma função sobrejetora é tal que, para todo \(b \in B\), existe pelo menos um \(a \in A\) tal que \(f(a)=b\). Como existem \(k^n\) funções de \(A\) em \(B\), vamos subtrair desse total o número de funções que não são sobrejetoras.

Considerando os elementos de \(B\), \(b_1, \ldots, b_k\), definimos \(C_i=\) “conjunto de todas as funções \(f:A\rightarrow B\) tais que \(f^{-1}(b_i)=\emptyset\)”, isto é, \(f(a)\neq b_i, \forall a \in A\). Como uma função deixa de ser sobrejetora quanto pertence a pelo menos um dos \(C_i\)´s, para \(i=1,2,\ldots, k\), o conjunto de todas as funções não-sobrejetoras é \[C_1 \cup C_2 \cup\cdots \cup C_k = \bigcup_{i=1}^{k}C_i.\] Logo, pelo Princípio da Inclusão e Exclusão, \[\Big|\bigcup_{i=1}^{k}C_i\Big| = \sum_{i=1}^{k}|C_i| - \sum_{1\leq i<j}^{}|C_i\cap C_j| + \sum_{1\leq i<j<l}^{}|C_i\cap C_j\cap C_l| + \cdots |C_1\cap\cdots\cap C_k|\]

Como \(|C_i|=(k-1)^n\), \(|C_i\cap C_j| = (k-2)^n, \ldots, |C_1\cap\ldots\cap C_k|=(k-k)^n\), temos \[\begin{align} \Big|\bigcup_{i=1}^{k}C_i\Big| &={k \choose 1}(k-1)^n - {k \choose 2}(k-2)^n + {k \choose 3}(k-3)^n + \cdots + {k \choose k}(k-k)^n \\ &=\sum_{i=1}^{k}(-1)^{i-1}{k \choose i}(k-i)^n. \end{align}\]

Subtraindo este número do total \(k^n\), temos

\[k^n-\sum_{i=1}^{k}(-1)^{i-1}{k \choose i}(k-i)^n = \sum_{i=0}^{k}(-1)^{i}{k \choose i}(k-i)^n.\]

3.2 Aula 12

3.2.1 Probabilidade

Definição 3.2 (Espaço amostral) O espaço amostral de um experimento é o conjunto de todos os resultados possíveis deste experimento. Notação: \(\mathcal{S}.\)

Exemplo 3.3 Defina o espaço amostral do seguinte experimento: ordem de chegada de uma corrida entre \(7\) pessoas numeradas de \(1\) a \(7\).

Solução. \(\mathcal{S}=\{\text{todas as $7!$ permutações de $\{1,2,3,4,5,6,7\}$}\}.\)

Exemplo 3.4 Defina o espaço amostral do seguinte experimento: resultado do lançamento de duas moedas.

Solução. O espaço amostral é formado pelos quatro elementos a seguir \[\mathcal{S}=\{(H,H),(H,T),(T,H),(T,T)\}.\] O resultado será \((H,T)\) se a primeira moeda der \(cara\) e a segunda \(coroa\).

Definição 3.3 (Evento) Qualquer subconjunto \(E\) do espaço amostral é conhecido como evento.

Em outras palavras, um evento é um conjunto formado pelos possíveis resultados do experimento. Se o resultado do experimento estiver contido em \(E\), dizemos que \(E\) ocorreu.

No Exemplo 3.3, considere \(E=\{\text{todos os resultados em $\mathcal{S}$ começando com $3$}\}\), então \(E\) é o evento em que a pessoa identificada pelo número \(3\) vence a corrida. Já no Exemplo 3.4, se \(E=\{(H,H),(H,T)\}\), então \(E\) é o evento em que a primeira moeda lançada dá \(cara\).

Para quaisquer dois eventos \(E\) e \(F\) de um espaço amostral \(\mathcal{S}\), definimos o novo evento \(E\cup F\) como sendo formado por todos os resultados que pertecem a \(E\) ou a \(F\) ou a \(E\) e \(F\) simultaneamente. Isto é, o evento \(E\cup F\) ocorrerá se \(E\) ou \(F\) ocorrer.

Exemplo 3.5 No Exemplo 3.4, se \(E=\{(H,H),(H,T)\}\) é o evento em que dá \(cara\) no primeiro lançamento e \(F=\{(T,H)\}\), então \(E\cup F=\{(H,H),(H,T),(T,H)\}\). Assim, \(E\cup F\) ocorreria se desse \(cara\) em qualquer uma das duas moedas.

Para quaisquer dois eventos \(E\) e \(F\) de um espaço amostral \(\mathcal{S}\), definimos o evento \(EF\) (ou \(E\cap F\)), chamado de interseção entre \(E\) e \(F\), como sendo formado por todos os resultados que estão tanto em \(E\) quanto em \(F\).

Exemplo 3.6 No Exemplo 3.4, se \(E=\{(H,H),(H,T),(T,H)\}\) é o evento em que pelo menos uma \(cara\) aparece nas duas moedas e \(F=\{(H,T),(T,H),(T,T)\}\) é o evento em que pelo menos uma coroa aparece, então \[E\cap F=\{(H,T),(T,H)\}\] é o evento em que exatamente uma \(cara\) e uma \(coroa\) aparecem.

Se \(EF=\emptyset\), então dizemos que \(E\) e \(F\) são mutualmente exclusivos.

3.2.2 Axiomas de Probabilidade

Uma maneira de definir a probabilidade de um evento é em termos de sua frequência relativa: suponhamos que um experimento, cujo espaço amostral é \(\mathcal{S}\), seja realizado repetidamente em condições exatamente iguais. Para cada evento \(E \subseteq \mathcal{S}\), definimos \(n(E)\) como o número de vezes que \(E\) ocorre nas \(n\) primeiras repetições do experimento. Então \(P(E)\), a probabilidade do evento \(E\), é definida como \[P(E) = \lim_{n \rightarrow \infty} \frac{n(E)}{n}.\]

Utilizando o R, vamos estimar a probabilidade de o lançamento de uma moeda dar cara através da frequencia relativa.

A simulação abaixo representa o resultado do lançamento de \(10\) moedas:

rbinom(n = 10, size = 1, prob = 0.5)

##  [1] 1 0 1 0 1 1 1 0 0 1

Vamos considerar que 1 representa cara e 0 coroa. Então, vamos realizar o experimento e calcular a probabilidade do evento \(E=\) “o lançamento dá cara”.

n=10
(m10 <- sum(rbinom(n, size = 1, prob = 0.5))/n)

## [1] 0.2

Veja que o resultado é P(E)=0.2.

Podemos repetir este experimento quantas vezes quisermos, por exemplo, para \(n=100,1000,10000,1000000\).

n=100
(m100 <- sum(rbinom(n, size = 1, prob = 0.5))/n)

## [1] 0.59

n=1000
(m100 <- sum(rbinom(n, size = 1, prob = 0.5))/n)

## [1] 0.51

n=10000
(m100 <- sum(rbinom(n, size = 1, prob = 0.5))/n)

## [1] 0.4964

n=100000
(m100 <- sum(rbinom(n, size = 1, prob = 0.5))/n)

## [1] 0.49939

A Figura 3.1 mostra o resultado deste experimento para n=1, 10, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000, 20000.

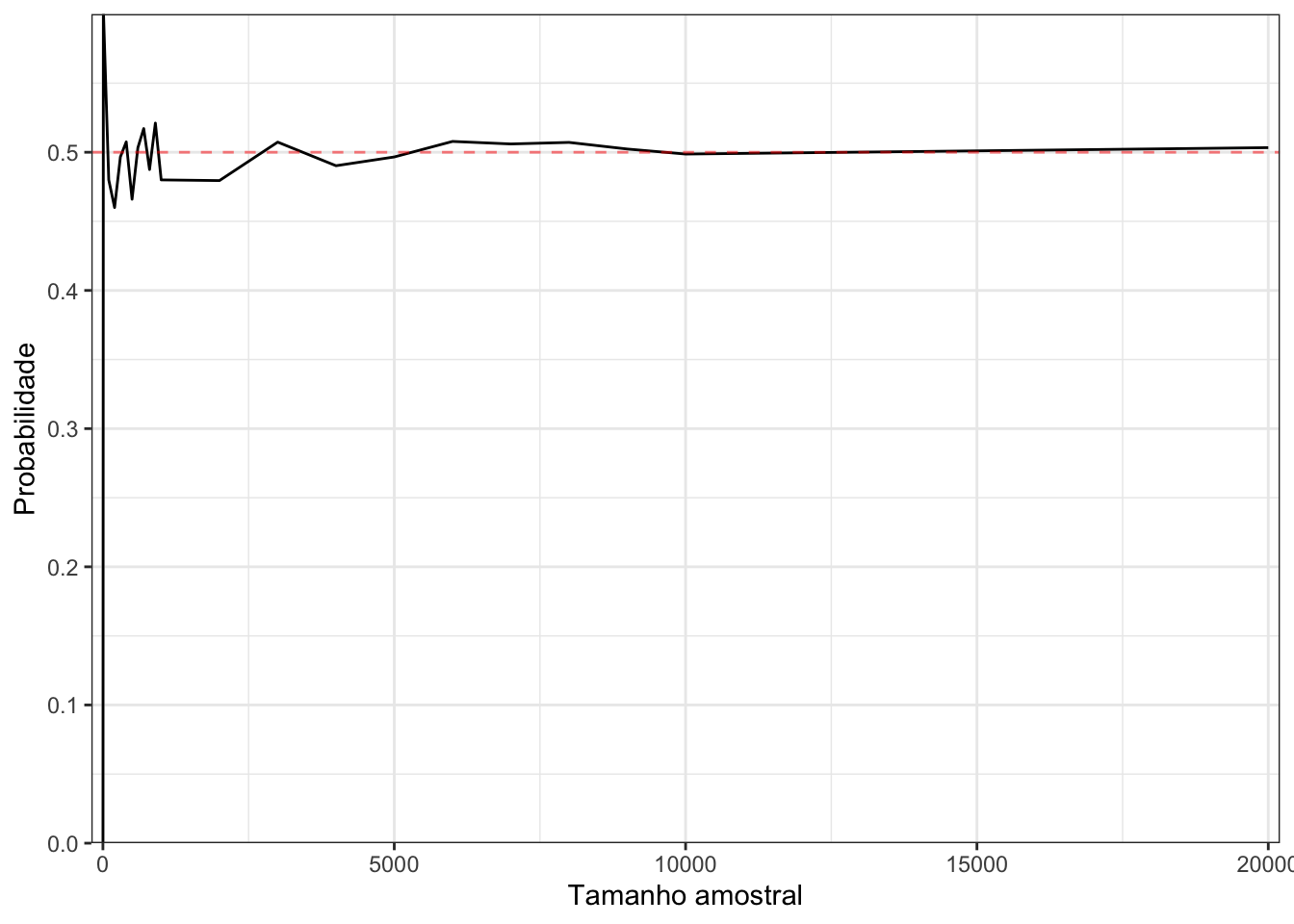
Figura 3.1: Simulação do lançamento de uma moeda para diferentes tamanhos amostrais

Há um inconveniente nesta definição: como saberemos que \(\frac{n(E)}{n}\) convergirá para algum valor limite constante que será o mesmo para cada possível sequência de repetições do experimento?

Vamos considerar a abordagem axiomática moderna da teoria da probabilidade. Então, vamos assumir que, para cada evento \(E \subseteq \mathcal{S}\), existe um valor \(P(E)\) chamado de probabilidade de ocorrência do evento \(E\). Vamos supor então que todas as probabilidade satisfazem certo conjunto de axiomas.

Considere um experimento cujo espaço amostral é \(\mathcal{S}\). Para cada evento \(E\) de \(\mathcal{S}\), assumimos que o número \(P(E)\) seja definido e satisfaça os três axiomas a seguir.

• Axioma 1: \(0 \leq P(E) \leq 1\);
• Axioma 2: \(P(S) = 1\);
• Axioma 3: para cada sequencia de eventos mutualmente exclusivos \(E_1, E_2, \ldots\) (ou seja, \(E_i E_j=\emptyset\) quando \(i\neq j\)), \(P\big(\cup_{i=1}^{\infty}E_i\big)=\sum_{i=1}^{\infty}E_i\).

Se considerarmos a sequência de eventos \(E_1, E_2, \ldots\), em que \(E_1=\mathcal{S}\) e \(E_i=\emptyset\) para \(i>1\), então, como os eventos são mutualmente exclusivos e \(\mathcal{S}=\cup_{i=1}^{\infty}E_i\), teremos, pelo Axioma 3, \[P(\mathcal{S})=\sum_{i=1}^{\infty}P(E_i) = P(\mathcal{S}) + \sum_{i=2}^{\infty}P(E_i),\] o que implica que \(P(\emptyset)=0\). Isto é, o evento vazio tem probabilidade nula. Daí seque que, para qualquer sequência de eventos mutualmente exclusivos \(E_1, E_2, \ldots, E_n\), \[P\Bigg(\bigcup_{i=1}^{\infty}E_i\Bigg) = \sum_{i=1}^{n}P(E_i).\]

3.3 Aula 13

Proposição 3.2 \[P(E^c) = 1 - P(E^c).\]

Em palavras, a Proposição 3.2 afirma que a probabilidade de um evento não ocorrer é igual à 1 menos a probabilidade dele ocorrer.

Prova. Note que \(E\) e \(E^c\) são sempre mutualmente exclusivos e, como \(E\cup E^c=\mathcal{S}\), temos, pelos Axiomas 2 e 3, \[1 = P(\mathcal{S}) = P(E\cup E^c) = P(E) + P(E^c)\]

Proposição 3.3 Se \(E \subset F\), então \(P(E) \leq P(F)\).

Prova. Como \(E \subset F\), podemos expressar \(F\) como \(F = E \cup E^c F\). Portanto, como \(E\) e \(E^c F\) são mutualmente exclusivos, obtemos, pelo Axioma 3, \[P(F) = P(E) + P(E^c F),\] o que prova o resultado, já que \(P( E^c F)\geq 0\).

Proposição 3.4 \[P(E \cup F) = P(E) + P(F) - P(E\cap F).\]

Prova. Note que \(E \cup F = E \cup E^c F\). Do Axioma 3 obtemos \[P(E \cup F) = P(E \cup E^c F) = P(E) + P(E^c F).\] Além disso, como \(F = EF\cup E^c F\), obtemos do Axioma 3 \[P(F) = P(EF) + P(E^c F),\] ou, equivalentemente, \(P(E^c F) = P(F) - P(EF)\), o que completa a demonstração.

Exemplo 3.7 Uma pessoa leva dois livros para ler durante as férias. A probabilidaide dela gostar do primeiro livro é \(0{,}5\), de gostar do segundo livro é \(0{,}4\) e de gostar de ambos os livros é \(0{,}3\). Qual a probabilidade de que essa pessoa não goste de nenhum dos livros?

Solução. Seja \(L_i\) o evento “a pessoa gosta do livro \(i\)”, \(i=1,2\). Então, a probabilidade dessa pessoa gostar de pelo menos um livro é \[P(L_1 \cap L_2) = P(L_1) + P(L_2) - P(L_1L_2) = 0{,}5+0{,}4-0{,}3=0{,}6.\]

Como o evento “a pessoa não gosta de nenhum dos livros” é o complementar do evento em que ela gosta de pelo menos um deles, obtemos como resultado \[P\big(L_1^c \cap L_2^c\big) = P\big((L_1^c \cup L_2)^c\big) = 1 - P\big(L_1^c \cup L_2\big) = 0{,}4.\]

Proposição 3.5 \[\begin{align} P(E_1\cup E_2 \cup\cdots\cup E_n) = \sum_{i=1}^{n}P(E_i) &- \sum_{1\leq i <j}P(E_i E_j) \\ &+ \cdots (-1)^{r+1}\sum_{1\leq i <j<\cdots<r}^{}P(E_i E_j \cdots E_r) +\cdots \\ &+(-1)^{n+1}P(E_1 E_2 \cdots E_n). \end{align}\]

Observação. A soma \(\sum_{1\leq i <j<\cdots<r}^{}P(E_i E_j \cdots E_r)\) é feita ao longo de todos os \({n \choose r}\) subconjuntos possíveis de tamanho \(r\) do conjunto \(\{1,2,3,\ldots, n\}.\)

Prova. Exercício! Dica: semelhante ao visto no Princípio de Inclusão e Exclusão (veja o Teorema 2.3).

Espaços amostrais com resultados igualmente prováveis

Em muitos experimentos é natural supor que todos os resultados presentes no espaço amostral sejam igualmente prováveis. Por exemplo, considere um experimento cujo espaço amostral \(\mathcal{S}\) é um conjunto finito, digamos \(\mathcal{S}=\{1,2,\ldots, n\}\). Se supormos que \[P(\{1\})= P(\{2\})= \cdots = P(\{n\}),\] então, pelos Axiomas 2 e 3, temos que (por quê?) \[P(\{i\})=\frac{1}{n}, \qquad i=1,2,\ldots, n.\] A partir da expressão acima e do Axioma 3, temos que, para cada evento \(E\),

\[P(E)=\frac{\text{número de resultados em }E}{\text{número de resultados em } \mathcal{S}}.\]

Exemplo 3.8 Se dois dados são lançados, qual é a probabilidade de que a soma das faces de cima seja igual a \(7\)?

Solução. Assumindo que os \(36\) resultados possíveis são equiprováveis, como há \(6\) resultados possíveis que resultam na soma dos dados se \(7\) – isto é, \((1,6),\) \((2,5),\) \((3,4), (4,3),\) \((5,2), (6,1)\) – a probabilidade desejada é igual a \(\frac{6}{36}=\frac{1}{6}.\)

Exemplo 3.9 Se três bolas são retiradas aleatoriamente de um recipiente contendo \(6\) bolas brancas e \(5\) bolas pretas, qual é a probabilidade de que uma das bolas seja branca e as outras duas sejam pretas?

Solução. Se considerarmos a ordem de seleção das bolas como sendo relevante, então o espaço amostral é formado por \(11\cdot 10\cdot 9 = 990\) resultados. Além disso, existem \(6\cdot 5\cdot 4 = 120\) resultados nos quais a primeira bola selecionada é branca e as outras duas são pretas; \(5\cdot 6\cdot 4 = 120\) resultados \(5\cdot 4\cdot 6 = 120\) resultados nos quais as primeiras duas bolas são pretas e a terceira é branca. Portanto, supondo que retiradas aleatoriamente signifique que cada evento do espaço amostral seja igualmente provável, vemos que a probabilidade desejada é \[\frac{120 + 120 + 120}{990}=\frac{4}{11}.\]

Solução. (alternativa) Podemos considerar o resultado do experimento como sendo o conjunto desordenado de bolas retiradas. Então, existem \({11 \choose 3}=165\) resultados no espaço amostral. Nesse caso, cada conjunto de 3 bolas corresponde a \(3!\) resultados quando a ordem de seleção é levada em consideração. Como consequência, se for considerado que todos resultados são equiprováveis quando a ordem da seleção é importante, tem-se que estes continuam equiprováveis quando o resultado considerado é um conjunto desordenado de bolas selecionadas. Dessa forma, usando esta última representação do experimentos, vemos que a probabilidade desejada é \[\frac{{6\choose 1}{5\choose 2}}{{11\choose 3}} = \frac{4}{11}.\]

3.4 Aula 14

Prova!