Capítulo 4 Semana 4
4.1 Aula 15
Solução. Como cada pessoa pode celebrar seu aniversário em qualquer um dos 365 dias do ano, há um total de \(365^n\) resultados possíveis (estamos considerando apenas anos não bisextos!). Supondo que cada resultado seja igualmente provável, vemos que a probabilidade desejada é igual a \[\frac{365\cdot 364\cdot 363 \cdots (365-n+1)}{365^n}.\]
Quando \(n\geq 23\), esta probabilidade é menor que \(\frac{1}{2}\). Isto é, 23 pessoas ou mais na sala, então a probabilidade de que pelo menos duas delas façam aniversário no mesmo dia é maior que \(\frac{1}{2}\).Solução. Seja \(E_i, i=1,2,\ldots,N\), o evento em que a \(i\)-ésima pessoa seleciona seu próprio chapeu. Pela Proposição 3.5, \(P(\cup_{i=1}^{N}E_i)\), a probabilidade de que pelo menos um dos presentes na festa selecione o seu próprio chapeu é dada por \[\begin{align} P(\cup_{i=1}^{N}E_i)=P(E_1\cup E_2 \cup\cdots\cup E_n) =& \sum_{i=1}^{N}P(E_i) - \sum_{1\leq i <j}P(E_i E_j) \\ &+ \cdots +(-1)^{N+1}P(E_1 E_2 \cdots E_N). \end{align}\]
Se interpretarmos o resultado deste experimento como um vetor de \(N\) números, em que o \(i\)-ésimo elemento corresponde ao número do chapeu jogado pela \(i\)-ésima pessoa, então existem \(N!\) resultados possíveis. Além disso, \(E_{i_1}E_{i_2}\cdots E_{i_n}\), o evento em que cada uma das \(n\) pessoas \(i_1, i_2, \ldots, i_n\) seleciona o seu próprio chapeu pode ocorrer de qualquer uma das \((N-n)(N-n-1)\cdots 1=(N-n)!\) maneiras possíveis, pois das \(N-n\) pessoas restantes, a primeira pode selecionar qualquer um dos \(N-n\) chapéus, a segunda pessoa pode selecionar qualquer um dos \(N-n-1\) chapéus restantes e assim por diante. Além disso, supondo que todos os \(N!\) resultados possíveis sejam igualmente prováveis, vemos que \[P(E_{i_1}E_{i_2}\cdots E_{i_n}) = \frac{(N-n)!}{N!}.\]
Além disso, como existem \({N \choose n}\) termos em \(\sum_{1\leq i_1<i_2 < \cdots < i_n}P(E_{i_1}E_{i_2}\cdots E_{i_n})\), temos que \[\sum_{1\leq i_1<i_2 < \cdots < i_n}P(E_{i_1}E_{i_2}\cdots E_{i_n}) = \frac{N!}{(N-n)!n!}\frac{(N-n)!}{N!} = \frac{1}{n!}.\] Logo, \[P\Bigg(\bigcup_{i=1}^{N}\Bigg) = 1 - \frac{1}{2!} + \frac{1}{3!} - \cdots + (-1)^{N+1}\frac{1}{N!}.\] Portanto, a probabilidade de que nenhuma das pessoas selecione o seu próprio chapeu é \[\begin{equation} 1 - P\Bigg(\bigcup_{i=1}^{N}\Bigg) = 1 - 1 + \frac{1}{2!} - \frac{1}{3!} + \cdots - (-1)^{N+1}\frac{1}{N!}. \tag{4.1} \end{equation}\]Probabilidade como uma medida de crença
Até agora interpretamos a probabilidade de um evento de certo experimento como sendo uma medida de frequência de ocorrência desse evento quando o experimento é repetido continuamente. Entretanto, existem também outros usos para o termo probabilidade. Por exemplo, você já deve ter ouvido frases como “a probabilidade de que Magno não seja paulista é de 90%”. Como podemos interpretar essa frase?
A interpretação mais simples e natural é que as probabilidades citadas são medidas da crença de um indivíduo. Essa interpretação da probabilidade como sendo uma medida de crença é chamada de visão pessoal ou subjetiva da probabilidade. Parece lógico supor que “uma medida de crença” deva satisfazer todos os axiomas da probabilidade. Por exemplo, se temos 60% de certeza de que Magno é mineiro e 15% de certeza de que ele é goiano, então é lógico supor que temos 75% de certeza de que Magno é mineiro ou goiano. Com isso, seja com a interpretação da probabilidade como uma medida de crença ou como uma frequência de ocorrência em uma longa sequência de experimentos, suas propriedades matemáticas permanecem inalteradas.
Vamos agora introduzir um dos conceitos mais importantes da teoria da probabilidade. A importância desse conceito é dupla. Em primeiro lugar, estamos frequentemente interessados em calcular probabilidades quando temos alguma informação parcial a respeito do resultado de um experimento; em tal situação, as probabilidades desejadas são condicionais. Em segundo lugar, mesmo quando não temos nenhuma informação parcial sobre o resultado de um experimento, as probabilidades condicionais podem ser frequentemente utilizadas para computar mais facilmente as probabilidades desejadas.
4.2 Aula 16
Probabilidade condicional e independência
Suponha que lancemos dois dados, cada um dos 36 resultados possíveis é igualmente provável e portanto tem probabilidade \(\frac{1}{36}\). Digamos que o primeiro dado seja um 3. Então, dada essa informação, qual é a probabilidade de que a soma dos dois dados seja 8?
Sabendo que saiu um 3 no dado inicial, existirão no máximo 6 resultados possíveis para o nosso experimento, isto é, \((3,1), (3,2),\) \((3,3), (3,4),\) \((3,5), (3,6)\). Como cada um desses resultados tinha originalmente a mesma probabilidade de ocorrência, os resultados deveriam continuar a ter probabilidades iguais. Dado que o primeiro dado é 3, a probabilidade (condicional) de cada um dos resultados possíveis é \(\frac{1}{6}\), enquanto a probabilidade (condicional) dos outros 30 pontos no espaço amostral é zero. Com isso, a probabilidade desejada será igual a \(\frac{1}{6}\).
Ao condicionar o evento \(E\) na ocorrência do evento \(F\), é como se \(F\) passase a ser o espaço amostral. Veja nas Figuras 4.1 e 4.2.
Figura 4.1: Espaço amostral e dois eventos.
Figura 4.2: Na probabilidade condicional, F faz o papel de espaço amostral.
Solução. Sejam \(B=\{(H,H)\}\) o evento em que ambos lançamentos dão cara, \(F=\{(H,H),(H,T)\}\) o evento em que dá \(cara\) no primeiro lançamento e \(A=\{(H,H),(H,T),(T,H)\}\) o evento em que pelo menos uma \(cara\) ocorre. Então, para o item (a) temos
\[\begin{align} P(B|F) &= \frac{P(BF)}{P(F)}\\ &=\frac{P(\{(H,H)\})}{P(\{(H,H),(H,T)\})} &&\\ &=\frac{1/4}{2/4}=\frac{1}{2}. \end{align}\]
E para o item (b)
\[\begin{align} P(B|A) &= \frac{P(BA)}{P(A)}\\ &=\frac{P(\{(H,H)\})}{P(\{(H,H),(H,T),(T,H)\})} &&\\ &=\frac{1/4}{3/4}=\frac{1}{3}. \end{align}\]Multiplicando ambos os lados da Expressão (4.2) por \(P(F)\), obtemos \[\begin{equation} P(E|F)P(F) = P(EF). \tag{4.3} \end{equation}\]
Solução. Defina os eventos \(R_1 =\) “primeira bola retirada é vermelha” e \(R_2 =\) “segunda bola retirada é vermelha”. (a) Dado que a primeira bola é vermelha, existem 7 bolas vermelhas e 4 bolas brancas restantes, de forma que \(P(R_2|R_1) = 7/11\). Como \(P(R_1)=8/12\), a probabilidade desejada é \[P(R_1 R_2) = P(R_1)P(R_2|R_1) = \frac{2}{3}\frac{7}{11} = \frac{14}{33}.\] Alternativamente, \(P(R_1 R_2) = {{8\choose 2}}/{{12\choose 2}}\).
Para o item (b) vamos usar \(P(R_1 R_2) = P(R_1)P(R_2 | R_1)\). Numere as bolas vermelhas e suponha que \(B_i, i=1, \ldots, 8\) seja o evento em que a primeira bola retirada é uma bola vermelha de numero \(i\). Então, \[P(R_1) = P\Bigg(\bigcup_{i=1}^{8}B_i\Bigg) = \sum_{i=1}^{8}P(B_i) = 8\cdot \frac{r}{8r+4w}.\]
Se a primeira bola é vermelha, a urna passa a conter 7 bolas vermelhas e 4 bolas brancas. Assim, pelo mesmo argumento acima, \[P(R_2 | R_1) = 7\cdot \frac{r}{7r+4w}.\] Portanto, a probabilidade desejada é \[P(R_1 R_2) = \frac{8r}{8r+4w}\frac{7r}{7r+4w}.\]Uma generalização da Equação (4.3) fornece uma expressão para a probabilidade da interseção de um número arbitrário de eventos.
\[\begin{equation} P(E_1 E_2 \cdots E_n) = P(E_1)P(E_2|E_1)P(E_3|E_1 E_2)\cdots P(E_n|E_1 E_2 \cdots E_{n-1}). \tag{4.4} \end{equation}\]
Fórmula de Bayes
Sejam os eventos \(E\) e \(F\). Podemos expressar \(E\) como \[E = EF \cup EF^c.\] Note que \((EF) \cap (EF^c)=\emptyset\), assim, pelo Axioma 3, \[\begin{align} P(E) &= P(EF) + P(EF^c)\\ &= P(E|F)P(F) + P(E|F^c)P(F^c). \tag{4.5} \end{align}\]
A Equação (4.5) diz que a probabilidade do evento \(E\) é uma média ponderada da probabilidade condicional de \(E\) dado que o evento \(F\) ocorreu e da probabilidade condicional de \(E\) dado que \(F\) não ocorreu. Esta fórmula é útil porque seu uso muitas vezes nos permite determinar a probabilidade de um evento com base na condição de ocorrência ou não de um segundo evento. Veja uma representação deste resultado através do diagrama de Venn na Figura 4.3.
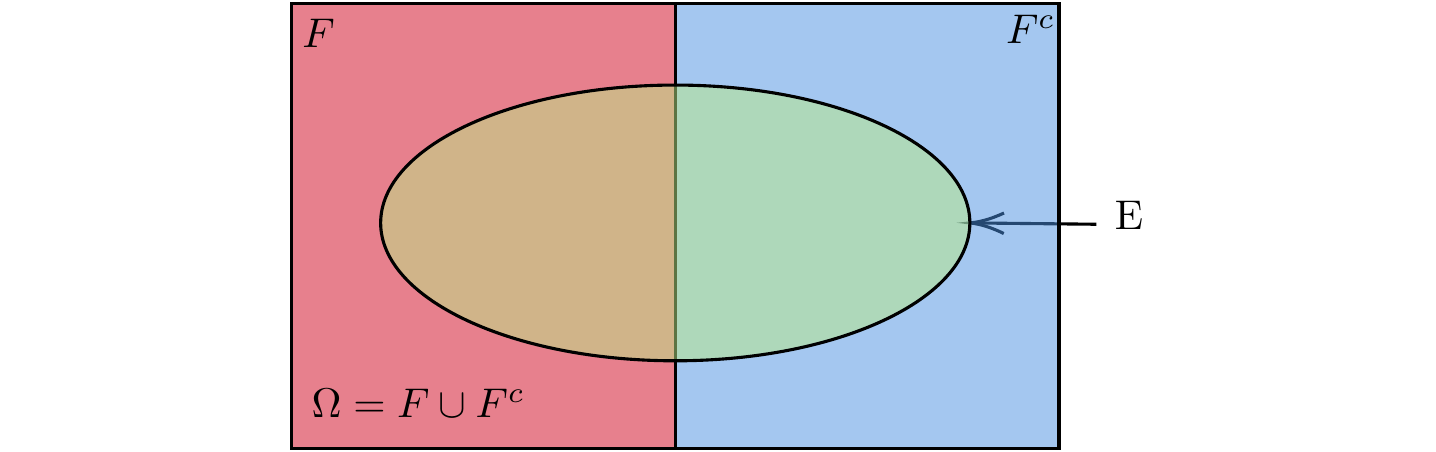
Figura 4.3: Na probabilidade condicional, F faz o papel de espaço amostral.
Solução. Vamos definir o evento \(A_1\) como sendo o evento em que “o segurado sofre um acidente no período de um ano após a compra de sua apólice” e \(A\) como “o segurado é propenso a acidentes”. Assim, a probabilidade desejada no item (a) é \[\begin{align} P(A_1) &= P(A_1|A)P(A) + P(A_1|A^c)P(A^c)\\ &= 0{,}4\cdot 0{,}3 + 0{,}2\cdot 0{,}7 = 0{,}26. \end{align}\]
Para o item (b), queremos obter \(P(A|A_1)\). Então,
\[P(A|A_1) = \frac{P(A A_1)}{P(A_1)} = \frac{P(A_1|A)P(A)}{P(A_1)} = \frac{ 0{,}3\cdot 0{,}4}{ 0{,}26} = \frac{6}{13} = 0{,}46.\]A Equação (4.5) pode ser generalizada da seguinte maneira. Suponha que \(F_1, F_2, \ldots, F_n\) sejam eventos mutualmente exclusivos tais que
\[\bigcup_{i=1}^{n}F_i=\mathcal{S}.\] Escrevendo \[E = \bigcup_{i=1}^{n}EF_i,\]
e usando o fato de que os eventos \(EF_i, i=1,\ldots, n\) são mutualmentne exclusivos, obtemos
\[\begin{equation} P(E) = \sum_{i=1}^{n}P(EF_i) = \sum_{i=1}^{n}P(E|F_i)P(F_i). \tag{4.6} \end{equation}\]
A Equação (4.6) mostra que, para dados eventos \(F_1, F_2, \ldots, F_n\), dos quais um e apenas um deve ocorrer, podemos calcular \(P(E)\) primeiro analizando as condições em que \(F_i\) ocorre. Além disso, a Equação (4.6) diz que \(P(E)\) é igual à média ponderada de \(P(E|F_i)\), com cada termo sendo ponderado pela probabilidade do evento ao qual está condicionado.
Considerando a mesma sequência de eventos \(F_1, F_2, \ldots, F_n\), uma partição de \(\mathcal{S}\), suponha que \(E\) tenha ocorrido e que estejamos interessados em determinar qual dos \(F_j\) ocorreu. Então pela generalização apresentada pela Equação (4.6), temos a Proposição 4.2 a seguir.
4.3 Aula 17
Solução. Vamos definir \(A\) como o evento “a lâmpada escolhida funciona mais do que 100h” e \(F_j\) como “a lâmpada do tipo \(j\) é escolhida”, para \(j=1,2,3\). Então, para o item (a) temos \[\begin{align} P(A) & = \sum_{j=1}^{3}P(A|F_j)P(F_j)\\ & = P(A|F_1)P(F_1) + P(A|F_2)P(F_2) + P(A|F_3)P(F_3)\\ & = 0{,}7\cdot 0{,}2 + 0{,}4\cdot 0{,}3 + 0{,}3\cdot 0{,}5\\ &= 0{,}41. \end{align}\]
Para o item (b), vamos usar a fórmula de Bayes (veja a Proposição 4.2)
\[P(F_j|A) = \frac{P(AF_j)}{P(A)} = \frac{P(A|F_j)P(F_j)}{0{,}41}.\]
Assim, \[\begin{align} P(F_1|A) &= \frac{0{,}7\cdot 0{,}2}{0{,}41} = \frac{11}{41} = 0{,}341, \\ P(F_j|A) &= \frac{0{,}4\cdot 0{,}3}{0{,}41} = \frac{12}{41} = 0{,}293, \\ P(F_j|A) &= \frac{0{,}3\cdot 0{,}5}{0{,}41} = \frac{15}{41} = 0{,}366. \end{align}\]
Note que, enquanto a probabilidade de uma lâmpada do tipo 1 ser escolhida é de apenas \(0{,}2\), a informação de que a lanterna funcionou por mais de 100 horas aumenta a probabildiade do evento \(E_1\) para \(0{,}341\).Eventos independentes
Até o momento, vimmos que \(P(E|F)\), a probabilidade condicional de \(E\) dado \(F\), não é geralmente igual a \(P(E)\). Ou seja, saber que \(F\) ocorreu geralmente muda a probabilidade de ocorrência de \(E\). Nos casos especiais em que \(P(E|F)\) é de fato igual a P(E), dizemos que \(E\) é independente de \(F\). Isto é, \(E\) é independente de \(F\) se o conhecimento de que \(F\) ocorreu não mudar a probabilidade de ocorrência de \(E\).
Solução. Sabemos que os 4 resultados possíveis deste experimento são \((h,h),(h,t),(t,h),(t,t)\), em que \(h\) representa cara e \(t\) representa coroa. Então, vamos verificar se existe independência entre \(E\) e \(F\) através da Definição 4.2. \[\begin{align} P(EF) &= P(\{(h,t)\}) = \frac{1}{4},\\ P(E) &= P(\{(h,h),(h,t)\}) = \frac{1}{2},\\ P(F) &= P(\{(h,t),(t,t)\}) = \frac{1}{2}.\\ \end{align}\]
Portanto, vemos que \(P(EF) = P(E)P(F)\), e \(E \perp F\).Prova. Suponha que \(E\) e \(F\) são independentes. Como \(E=EF\cup EF^c\) e \((EF)\cap (EF^c)=\emptyset\), temos
\[\begin{align} P(E) &= P(EF) + P(EF^c)\\ &=P(E)P(F) + P(EF^c). \end{align}\]
Equivalentemente, \[\begin{align} P(EF^c) &= P(E) - P(E)P(F)\\ &=P(E)\big[1-P(F)\big].\\ &=P(E)P(F^c). \end{align}\]
Variáveis Aleatórias discretas
Ao realizar um experimento, frequentemente estamos interessados principalmente em alguma função do resultado e não do resultado em si. Essas grandezas de interesse, ou essas funções reais definidas no espaço amostral, são conhecidas como variáveis aleatórias. Como o valor da variável aleatória é determinado pelo resultado do experimento, podemos atribuir probabilidades à estes possíveis valores.
Para uma variável discreta \(X\), definimos a função discreta de probabilidade (ou simplesmente função de probabilidade) \(p(a)\) de \(X\) como \[p(a) = p(\{X=a\}).\]
A função discreta de probabilidade p(a) é positiva para no máximo um número contável de valores de a. Isto é, se \(X\) deve assumir um dos valores \(x_1, x_2, \ldots,\) então \[\begin{align} p(x_i) &\geq 0 \quad \text{para } i=1,2,\ldots\\ p(x) &= 0 \quad \text{para todos os demais valores de } x. \end{align}\]
Como \(X\) deve assumir um dos valores \(x_i\), \[\sum_{i=1}^{\infty}p(x_i)=1.\]
4.4 Aula 18
Solução. Seja \(X\) o maior número selecionado. Então \(X\) é uma variável aleatória que pode ter qualquer um dos valores \(3, 4, \ldots, 20\). Se supormos que cada uma das \({20\choose 3}\) seleções possíveis tem a mesma probabilidade de ocorrer, então \(P(X=i) = {{i-1} \choose 2}/{20\choose 3},\) \(i = 3, 4, \ldots, 20.\)
Temos, então, que \(P(X \geq 17)=\) \(P(X=17) +\) \(P(X=18) +\) \(P(X=19) +\) \(P(X=20) =\) \(0{,}509.\)A função de distribuição acumulada \(F\) pode ser expressa em termos de \(p(a)\) como \[F(a) = \sum_{x \leq a}p(x).\]
Exemplo 4.15 Se \(X\) tem uma função de probabilidade dada por \[p(1) = \frac{1}{4}, \quad p(2) = \frac{1}{2}, \quad p(3) = \frac{1}{8}, \quad p(4) = \frac{1}{8},\] então, sua função de distribuição acumulada é
\[\begin{equation*} F(a) = \begin{cases} 0 & \text{se } a < 1\\ 1/4 & \text{se } 1 \leq a < 2\\ 3/4 & \text{se } 2 \leq a < 3\\ 7/8 & \text{se } 3 \leq a < 4\\ 1 & \text{se } 4 \leq a\\ \end{cases} \end{equation*}\]A Figura 4.4 mostra o gráfico da função \(F(x).\)
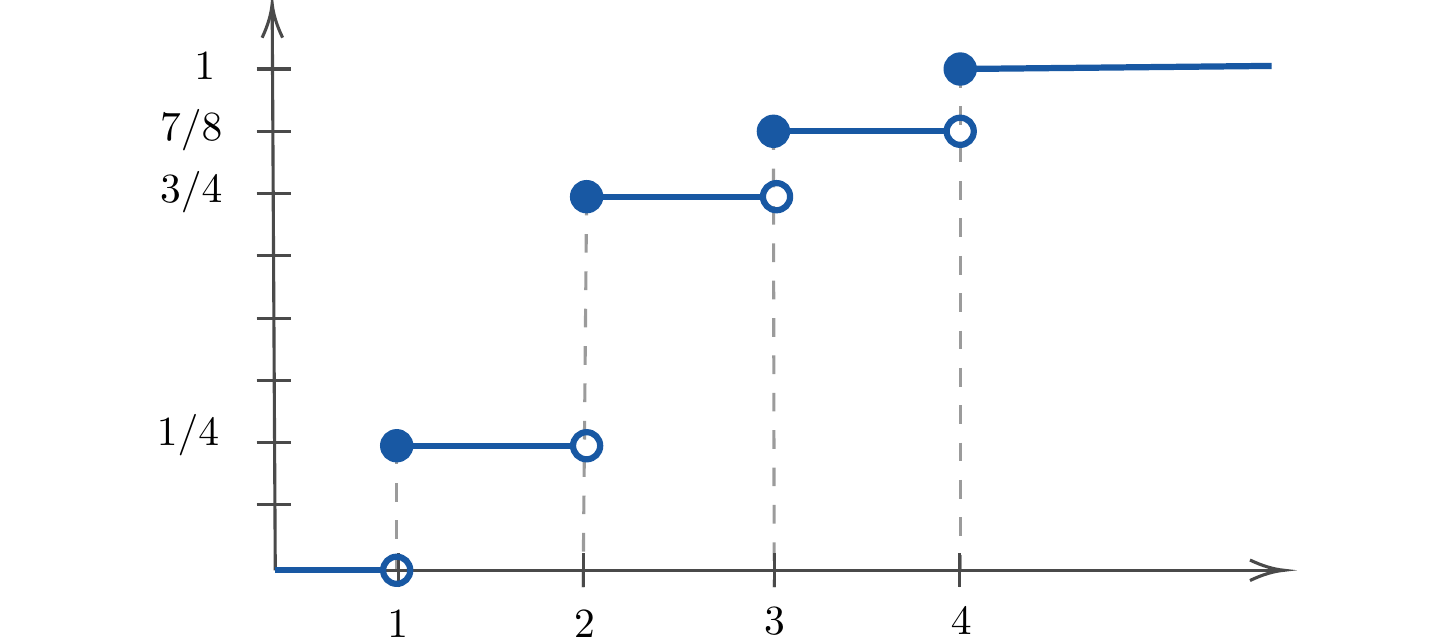
Figura 4.4: Roda com cinco crianças.
Valor esperado
Um dos conceitos mais importantes na teoria da probabilidade é aquele do valor esperado de uma variável aleatória.
Note que \(E(X)\) é uma média ponderada dos possíveis valores que \(X\) pode assumir, com cada valor sendo ponderado pela probabilidade de que \(X\) seja igual a esse valor.
Solução. Como \(p(1)=\) \(p(2)=\) \(p(3)=\) \(p(4)=\) \(p(5)=\) \(p(6)=\) \(1/6\), temos
\[E(X) = 1\cdot \frac{1}{6} +2\cdot \frac{1}{6}+3\cdot \frac{1}{6}+4\cdot \frac{1}{6}+5\cdot \frac{1}{6}+6\cdot \frac{1}{6}=\frac{7}{2}.\]4.5 Aula 19
Seja \(X\) uma variável aleatória discreta e suponha que queriamos calcular o valor esperado de alguma função de \(X\), digamos \(g(X)\). Como \(g(x)\) é uma variável aleatória discreta, ela tem função de probabilidade que pode ser determinada a partir da função de probabilidade de \(X\), assim, podemos calcular \(E[g(x)]\) usando a Definição 4.5.
O Corolário 4.1 é uma consequência direta da Proposição 4.4.
O valor esperado de uma variável aleatória \(X\), \(E(X)\), também é chamado de média ou primeiro momento de \(X\). A grandeza \(E(X^n)\), \(n\geq 1\),é chamada de \(n\)-ésimo momento de \(X\). Pela Proposição 4.4, temos que \[E(X^n) = \sum_{x:p(x)> 0}x^n p(x).\]
Variância
Dada uma variável aleatória X e sua função distribuição \(F\), seria extremamente útil se pudéssemos resumir as propriedades essenciais de F em certas medidas convenientemente definidas. Uma dessas medidas seria \(E(X)\) o, valor esperado de \(X\). Entretanto, embora \(E(X)\) forneça a média ponderada dos valores possíveis de \(X\), ela não nos diz nada sobre a variação, ou dispersão, desses valores.
O valor esperado de \(W, Y\) e \(Z\) é igual a 0, embora exista uma dispersão muito maior nos valores possíveis de \(Y\) do que naqueles de \(W\) (que é uma constante) e nos valores possíveis de \(Z\) do que naqueles de \(Y\).
Por esse motivo, é interessante também analisar uma variável aleatória olhando para sua disperção. Uma medida de dispersão que é bastante utiliada é a variância.
Uma fórmula alternativa para o cálculo de \(\mathrm{Var}(X)\) é deduzida a seguir.
\[\begin{align} \mathrm{Var}(X) &= E\big[(X-\mu)^2\big] \\ &= \sum_x (x-\mu)^2p(x) \\ &= \sum_x (x^2 - 2\mu x + \mu^2)p(x)\\ &= \sum_x x^2p(x) - 2\mu\sum_x xp(x) + \mu^2\sum_x p(x)\\ &= E(X^2) - 2\mu^2 + \mu^2\\ &= E(X^2) - \mu^2. \end{align}\]
Assim, \[\mathrm{Var}(X) = E\big(X^2\big)-\big[E(X)\big]^2.\] Na prática, essa é uma maneira mais fácil de calcular \(\mathrm{Var}(X)\).