Capítulo 2 Semana 2
2.1 Aula 6
Atenção! No Exemplo 1.26, obtivemos 20 números de 2 algarismos diferentes e no Exemplo 2.1 obtivemos 10 subconjuntos de 2 elementos. Observe que \(12 \neq 21\), mas \(\{1,2\}=\{2,1\}\). Pelo princípio multiplicativo, obtivemos \(5\times 4=20\), considerando a ordem de colocação dos dígitos. Na formação de subconjuntos a ordem não importa, devemos dividir o resultado anterior por \(2 = 2\times 1 = 2!\), isto é, pela permutação de 2 que é o número de elementos em cada subconjunto.
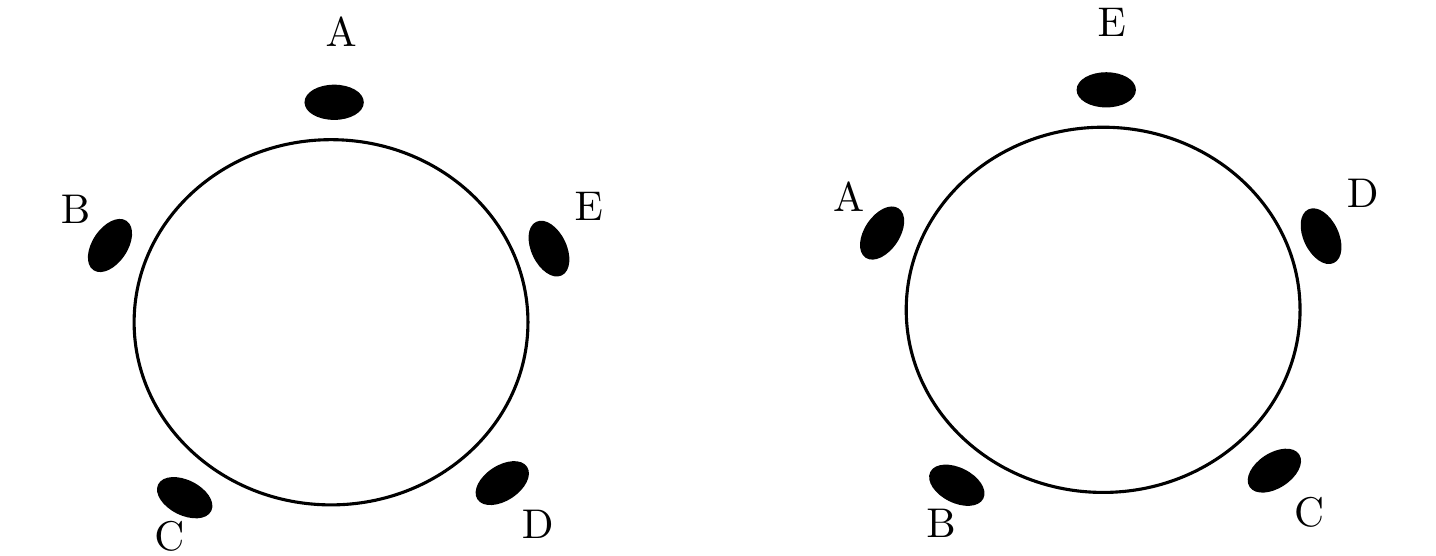
Figura 2.1: Roda com cinco crianças.
Solução. Ao fatorá-lo, obtemos \(N=126000=2^4\cdot 3^2\cdot 5^3\cdot 7\). Note que nos divisores de \(N\)
- o expoente do fator \(2\) pode variar de 0 a 4 (\(2^0, 2^1, 2^2, 2^3, 2^4\));
- o expoente do fator \(3\) pode variar de 0 a 2 (\(3^0, 3^1, 3^2\));
- o expoente do fator \(5\) pode variar de 0 a 3 (\(5^0, 5^1, 5^2, 5^3\));
- o expoente do fator \(7\) pode variar de 0 a 1 (\(7^0, 7^1\)).
Então, representando os divisores de \(N\) como números da forma
\[D = 2^x\cdot 3^y\cdot 5^z\cdot 7^w,\]
podemos dizer que
- \(x\) toma valores em \(\{0,1,2,3,4\}\), i.e. \(5\) possibilidades para \(x\);
- \(y\) toma valores em \(\{0,1,2\}\), i.e. \(3\) possibilidades para \(y\);
- \(z\) toma valores em \(\{0,1,2,3\}\), i.e. \(4\) possibilidades para \(z\);
- \(w\) toma valores em \(\{0,1\}\), i.e. \(2\) possibilidades para \(w\).
Arranjo simples (\(r\)-permutação)
Vamos encontrar uma expressão matemática que caracterize \(A^{r}_{n}\). Temos \(n\) elementos dos quais queremos tomar \(r\). Isto equivale a preencher \(r\) lugares com \(n\) objetos.
\[ \underbrace{\_\_}_{L_1}\underbrace{\_\_}_{L_2}\underbrace{\_\_}_{L_3}\cdots\underbrace{\_\_}_{L_r} \]
No primeiro lugar há \(n\) objetos diferentes que podem ser escolhidos. No segundo lugar há \(n-1\) objetos diferentes (lembre-se que um já foi escolhido). No terceiro lugar há \(n-2\) objetos diferentes, e assim sucessivamente, de forma que \(L_r\) terá \(n-(r-1)\) maneiras diferentes de ser preenchido. Pelo Princípio Multiplicativo, podemos dizer que as \(r\) posições podem ser preenchidas sucessivamente de \(n(n-1)(n-2)\cdots(n-(r-1))\) maneiras distintas. Portanto \[\begin{equation} A^{r}_{n} = n(n-1)(n-2)\cdots(n-(r-1)). \tag{2.1} \end{equation}\]
Multiplicando e dividindo por 1, temos que
\[ A^{r}_{n} = n(n-1)(n-2)\cdots(n-(r-1))\frac{(n-r)(n-r-1)\cdots2\cdot 1}{(n-r)(n-r-1)\cdots2\cdot 1} = \frac{n!}{(n-r)!}. \]
Solução. Os números que buscamos tem 4 dígitos, ou 4 posições a serem preenchidas
\[ \underbrace{\_\_}_{p_1}\underbrace{\_\_}_{p_2}\underbrace{\_\_}_{p_3}\underbrace{\_\_}_{p_4}. \]
Para resolver o item (a), note que números pares tem na última posição 0, 2, 4, 6 ou 8.
números terminados em 0: \(\underbrace{\_\_}_{p_1}\underbrace{\_\_}_{p_2}\underbrace{\_\_}_{p_3}\underbrace{0}_{p_4}\). Com excessão do zero, dígitos disponíveis: \(1,2,\ldots,9\). Preenchemos as três primeiras posiçõeos de \(A^{3}_{9}=\frac{9!}{6!}=504\) maneiras.
números terminados em 2, 4, 6 ou 8: Preenchimento da última posição: 4 maneiras. Preenchimento da primeira posição: 8 maneiras (exclui-se 0 e o dígito em \(p_4\)). Preenchemos as posições \(p_2\) e \(p_3\) de \(A^{2}_{8}=\frac{8!}{6!}=56\) maneiras. Pelo Princípio Multiplicativo, há \(4\cdot 8\cdot A^{2}_{8} = 1792\) números pares com dígitos distintos que não terminam em zero.
Finalmente, pelo Princípio Aditivo, há \(A^{3}_{9} + 4\cdot 8 \cdot A^{3}_{9} = 2296\) números pares entre 1000 e 9999 com dígitos distintos.
No item (b), se os números são constituidos de dígitos ímpares, então são formados pelos dígitos 1, 3, 5, 7 e 9. Portanto há \(A^4_5=5!=120\) números entre 1000 e 9999 formados de dígitos ímpares.2.2 Aula 7
Combinações
Note que, no Exemplo 2.10, os conjuntos de tamanho \(3\) são uma bijeção entre os conjuntos de tamanho \(1\), já que todo conjunto de tamanho \(3\) é o complemento de conjunto de tamanho \(1\). Em geral, é verdade que o número de subconjuntos com \(k\) elementos é igual ao número de subconjuntos com \(n-k\) elementos.
Prova. Claramente, quando \(k \notin \{0, 1, \cdots, n\}\), temos que \({n \choose k} = 0\). Temos também que \({0 \choose 0} = 1\), pois o conjunto vazio é o único subconjunto de tamanho zero. Se \(n\geq 1\), temos que considerar os casos em que \(k=0\) e \(k=n\) separadamente.
Se \(k=0\), então o único subconjunto de \(\{0, 1, \ldots, n\}\) com zero elementos é o conjunto vazio, assim \[ {n \choose 0} = 1 = {n-1 \choose 0} + {n-1 \choose -1} = 1+0.\]
Se \(k=n\), então o único subconjunto de \(\{0, 1, \ldots, n\}\) com \(n\) elementos é o próprio \(\{0, 1, \ldots, n\}\), assim, \[ {n \choose n} = 1 = {n-1 \choose n} + {n-1 \choose n-1} = 0+1.\]
Se \(1 \leq k \leq n-1\), então existem dois tipos de subconjuntos de \(\{0, 1, \ldots, n\}\) com \(k\) elementos: aqueles que contém \(n\) e aqueles que não contém \(n\). O número de subconjuntos de \(k\) elementos de \(\{0, 1, \ldots, n\}\) contendo \(n\) é igual ao número de subconjuntos de \(\{0, 1, \ldots, n-1\}\) contendo \(k-1\) elementos, que é denotado por \({n-1 \choose k-1}\). O número de subconjuntos de \(k\) elementos de \(\{0, 1, \ldots, n\}\) que não contém \(n\) é igual ao número de subconjuntos de \(\{0, 1, \ldots, n-1\}\) contendo \(k\) elementos, que é denotado por \({n-1 \choose k}\). Então, o número de subconjuntos de \(\{0, 1, \ldots, n\}\) com \(k\) elementos é \[ {n \choose k} = {n-1 \choose k} + {n-1 \choose k-1}.\]
Através da relação de Stifel, pode-se criar um triângulo numérico infinito formado por coeficientes binomiais, como mostrado na Firgura 2.2. Este é conhecido como Triângulo combinatório.

Figura 2.2: Triângulo combinatório.
Prova. Vamos usar indução sobre n para fazer a prova.
Para \(n=0\). Como \(0 \leq k \leq n\), temos que \(k=0\), logo \({0 \choose 0} =1\), \[\frac{0!}{0!(0)!}=1.\]
Hipótese de indução: supor que se cumpre para n-1.
Verificar que vale para \(n\).
Pela fórmula de Pascal \[\begin{align} {n \choose k} &= {n-1 \choose k} + {n-1 \choose k-1} \\ &= \frac{(n-1)!}{k!(n-1-k)!} + \frac{(n-1)!}{(k-1)!(n-1-(k-1))!} \\ &= \frac{(n-1)!}{k!(n-1-k)!} + \frac{(n-1)!}{(k-1)!(n-k)!} \\ &= \frac{(n-k)}{(n-k)}\frac{(n-1)!}{k!(n-1-k)!} + \frac{k}{k}\frac{(n-1)!}{(k-1)!(n-k)!} \\ &= \bigg(\frac{n-k}{k!(n-k)(n-k-1)!} + \frac{k}{k(k-1)!(n-k)!} \bigg)(n-1)! \\ &= \bigg(\frac{n-k}{k!(n-k)!} + \frac{k}{k!(n-k)!} \bigg)(n-1)! \\ &= \frac{n}{k!(n-k)!}(n-1)! \\ &= \frac{n!}{k!(n-k)!}. \end{align}\]
2.3 Aula 8
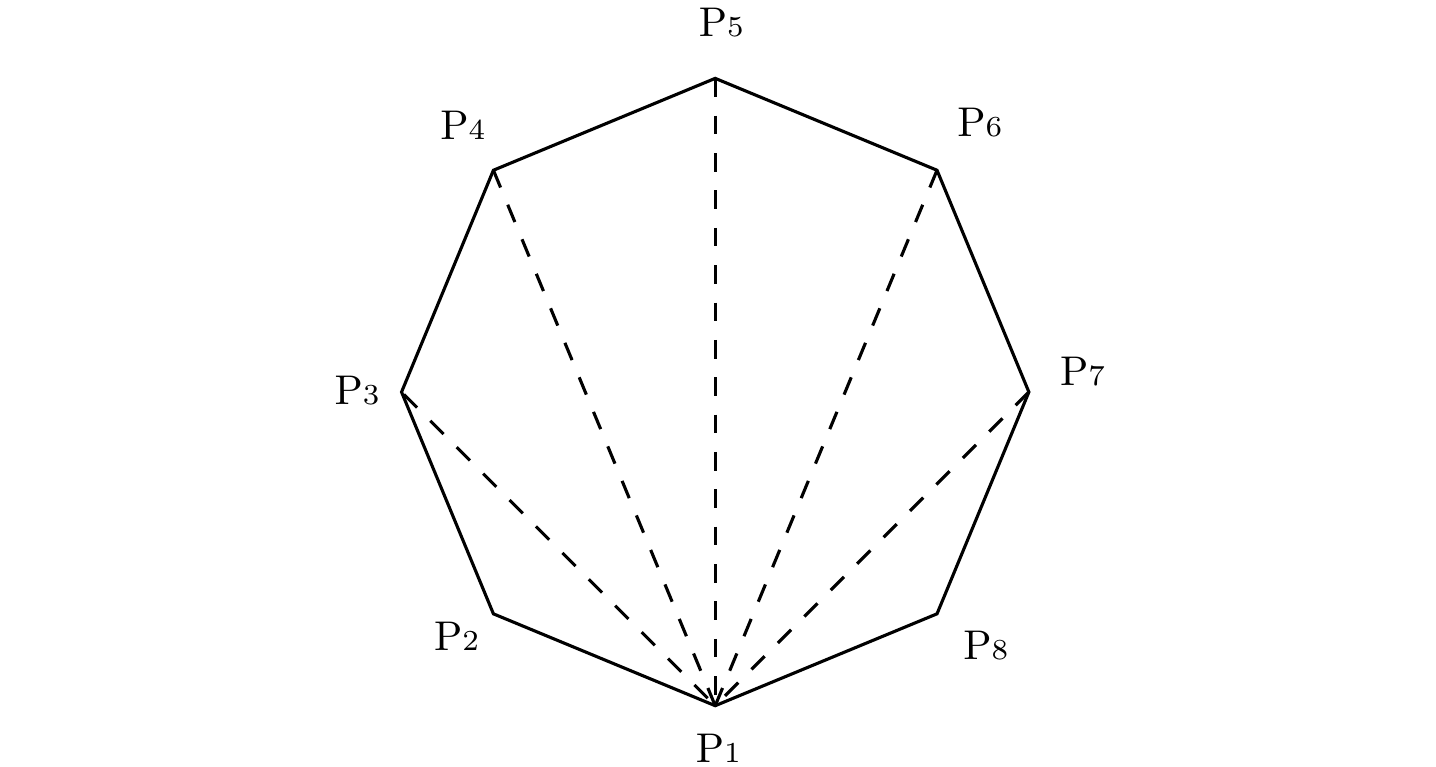
Figura 2.3: Polígono regular de 8 lados.
Solução. Sejam os conjuntos
\[\begin{align} \mathcal{A}_1 &= \{x \in \mathcal{A} | x=3k, k=1,2,\ldots \} = \{3, 6, 9, \ldots, 48\},\\ \mathcal{A}_2 &= \{x \in \mathcal{A} | x=3k+1, k=1,2,\ldots \} = \{1, 4, 7, 10, \ldots, 49\},\\ \mathcal{A}_3 &= \{x \in \mathcal{A} | x=3k+2, k=1,2,\ldots \} = \{2, 5, 8, 11, \ldots, 50\}.\\ \end{align}\]
Vamos denominar \(n(\mathcal{A}_i)\) a cardinalidade de \(\mathcal{A}_i\). Então, \[n(\mathcal{A}_1) = 16, \qquad n(\mathcal{A}_2)=17, \qquad n(\mathcal{A}_3)=17.\]
Se somarmos \(3\) números quaisquer de \(\mathcal{A}_1\), teremos como soma um múltiplo de \(3\), pois se \(x,y,z \in \mathcal{A}_1\), então \(x+y+z = 3(k + k^{\prime} + k^{\prime\prime})\), em que \(k, k^\prime, k^{\prime\prime} \in \mathbb{N}\). Essa soma pode ser feita de \(C^{3}_{16} = \frac{16!}{3!13!}=560\) maneiras.
Se somarmos 3 números quaisquer de \(\mathcal{A}_2\), teremos como soma um múltiplo de \(3\), pois se \(x,y,z \in \mathcal{A}_2\), então \(x+y+z =(3k+1)+(3k^{\prime}+1)+(3k^{\prime\prime}+1)=3(k + k^{\prime} + k^{\prime\prime})+3\), em que \(k, k^\prime, k^{\prime\prime} \in \mathbb{N}\). Essa soma pode ser feita de \(C^{3}_{17} = \frac{17!}{3!14!}=680\) maneiras.
Se somarmos 3 números quaisquer de \(\mathcal{A}_3\), teremos como soma um múltiplo de \(3\), pois se \(x,y,z \in \mathcal{A}_3\), então \(x+y+z =(3k+2)+(3k^{\prime}+2)+(3k^{\prime\prime}+2)=3(k + k^{\prime} + k^{\prime\prime})+6\), em que \(k, k^\prime, k^{\prime\prime} \in \mathbb{N}\). Essa soma pode ser feita de \(C^{3}_{17} = \frac{17!}{3!14!}=680\) maneiras.
Se somarmos \(1\) elemento de \(\mathcal{A}_1\) com \(1\) elemento de \(\mathcal{A}_2\) e com \(1\) elemento de \(\mathcal{A}_3\), obteremos como soma um múltiplo de \(3\), pois se \(x \in \mathcal{A}_1\), \(y \in \mathcal{A}_2\) e \(z \in \mathcal{A}_3\), então \(x+y+z =\) \(3k+(3k^{\prime}+1)+(3k^{\prime\prime}+2)=\) \(3(k + k^{\prime} + k^{\prime\prime})+3\), em que \(k, k^\prime, k^{\prime\prime} \in \mathbb{N}\). Essa soma pode ser feita de \(C^{1}_{16}C^{1}_{17}C^{1}_{17} = 16 \cdot 17 \cdot 17 = 4624\) maneiras.
Portanto, podemos escolher \(3\) números distintos de \(\mathcal{A}\), de modo a obter um múltiplo de \(3\), de \(C^{3}_{16}+C^{3}_{17}+C^{3}_{17}+C^{1}_{16}C^{1}_{17}C^{1}_{17} = 6544\) maneiras.Neste caso explorado pelo Exemplo 2.16 foi fácil enumerar. Entretanto, para um conjunto com \(10\) elementos, a solução não seria tão fácil de ser determinada. Vamos encontrar uma maneira de contar o número de subconjuntos sem que haja a necessidade de enumerá-los. Vamos marcar com o sinal “\(+\)” os elementos que farão parte do subconjunto e com o sinal “\(-\)” os elementos que não farão parte do subconjunto. Dessa forma, \(\{1,3\}\) pode ser representado por \(+-+--\), \(\{2,5\}\) pode ser representado por \(-+--+\), e \(\{1,2\}\) pode ser representado por \(++---\), que não é um conjunto válido, de acordo com as condições do enunciado. Veja que para formar o subconjunto desejado, devemos colocar 3 sinais “\(-\)” e 2 sinais “\(+\)” em fila, sem que haja dois sinais “\(+\)” consecutivos. Isto pode ser feito se colocarmos os \(3\) sinais “\(-\)” e deixarmos espaços entre eles, onde eventualmente colocaremos os sinais “\(+\)”. \[\_\_ - \_\_ - \_\_ - \_\_ .\] Há \(4\) posições vazias, e, para colocarmos os dois sinais “\(+\)”, basta escolhermos \(2\) dentre estas \(4\) posições. Consequentemente, há \(C^2_4=6\) maneiras disso ser feito e, portanto, há \(6\) subconjuntos de \(2\) elementos não consecutivos de \(A\).
2.4 Aula 9
2.4.1 Aplicações
2.4.1.1 Equações lineares com coeficientes unitários
O objetivo aqui é contar o número de soluções inteiras de uma equação da forma
\[\begin{equation} x_1 + x_2 + x_3 + \cdots + x_n = m, \tag{2.2} \end{equation}\]
em que \(x_i\), para \(i=1,2,\ldots, n\), e \(m\) são inteiros.
Prova. Como estamos interessados em expressar o inteiro positivo \(m\) como soma de \(n\) inteiros positivos, basta colocarmoms \(n-1\) barras divisoras entre os \(m\) \(1\)´s:
\[1 + 1 \vert + 1 + \cdots +1 \vert +1 \cdots + 1 \vert + 1 + \cdots + 1 =m.\]
O valor de \(x_1\) será o número de \(1\)´s que antecedem a primeira barra, o valor de \(x_2\) será o número de \(1\)´s entre a primeira e a segunda barra, e assim por diante, até obtermos o valor de \(x_n\) como sendo o número de \(1\)´s à direita da barra de número \(n-1\). Como a cada possível distribuição das barras corresponde uma única solução para a equação acima, basta contarmos de quantas formas isso pode ser feito. Devemos selecionar \(n-1\) dos \(m-1\) possíveis locais (os sinais de “\(+\)” que separam os \(1\)´s) para a colocação das barras divisórias, o que pode ser feito de \(C^{n-1}_{m-1}\) maneiras diferentes.Solução. Algumas soluções procuradas são \((4,5,8)\), \((5,7,5)\) e \((9,4,4)\). Subtraindo \(3\) unidades de cada componente destas ternas ordenadas, obtemos \((1,2,5)\), \((2,4,2)\) e \((6,1,1)\), respectivamente, que são soluções em inteiros positivos da equação \[\begin{equation} y_1 + y_2 + y_3 = 8, \qquad y_i\geq 1, \tag{2.4} \end{equation}\]
em que \(y_i=x_i-3\), \(i=1,2,3\). Como o número de soluções da Equação (2.4) é \(C^2_7=21\), este é o número procurado, uma vez que esta mudança de variável descrita acima estabelece uma relação biunívoca entre os conjuntos de soluções das duas equações.2.4.1.2 Combinações com repetições
Solução. É claro que ela pode comprar dois bilhetes do mesmo tipo. A lista de possibilidades é
\[\begin{align} aa, &\quad ab, \quad ac, \quad ad, \quad bb, \\ bc, &\quad bd, \quad cc, \quad cd, \quad dd. \tag{2.5} \end{align}\] $$$$
Veja que este número de possibilidades é maior que \(C^2_4=6\).As combinações listadas na Expressão (2.5) são chamadas combinações com repetição.
Retomando o contexto apresentado no Exemplo 2.19, se uma pessoa tem dinheiro para comprar \(5\) bilhetes, algumas possibilidades seriam
\[aaaaa, \quad abbbc, \quad bbccd.\] Estamos interessados em contar o total de elementos do tipo acima. Para saber os bilhetes comprados, basta que a pessoa nos diga quantos bilhetes de cada tipo ela comprou. Sejam \(x_1, x_2, x_3, x_4\) o número de bilhetes comprados para os brinquedos \(a,b,c,d\), respectivamente. O que estamos procurando é o número de soluções inteiras não-negativas para a equação \[x_1+x_2+x_3+x_4=5,\] que, como sabemos, através do Teorema 2.2, é \(C^3_8=56\), e vamos denotar por \(CR^4_5\).
Podemos generalizar o resultado anterior. Assim, \(CR^p_n\) é o número total de maneiras de selecionarmos \(p\) objetos dentre \(n\) objetos distintos, em que cada objeto pode ser escolhido até \(p\) vezes, que, como vimos, é igual ao número de soluções não negativas da equação \[x_1+x_2+\cdots x_p=n,\] que é \[C^{n-1}_{n+p-1}=C^{p}_{n+p-1}.\] Logo temos que \[CR^{p}_{n}=CR^{p}_{n+p-1}.\]
2.5 Aula 10
2.5.0.1 Arranjo com repetições
Lembre que, pela Expressão (2.1), \[A^{r}_{n} = n(n-1)(n-2)\cdots(n-(r-1)).\] Este número conta todas as possíveis maneiras de se retirar, de um conjuntos de \(m\) elementos distintos, \(p\) elementos, levando-se em conta a ordem dos elementos.
Caso sejam permitidas repetições, o princípio multiplicativo nos diz que o número total de maneiras de se retirar, levando-se em conta a ordem, \(p\) dos \(m\) objetos, distintos ou não, é igual a \[AR_m^p = m^p,\] uma vez que o primeiro elemento pode ser retirado de \(m\) maneiras distintas, o segunto também de \(m\) maneiras, e assim sucessivamente, até que o \(p\)-ésimo seja escolhido.
2.5.1 Princípio da inclusão e exclusão
Queremos obter uma fórmula que forneça o número total de elementos na união de um número finito de conjuntos. Considere o diagrama mostrado na Figura 2.4, com os conjuntos \(A\) e \(B\). O número total de elementos da união \(A \cup B\) é \[|A\cup B| = |A| + |B| - |A\cap B|.\]
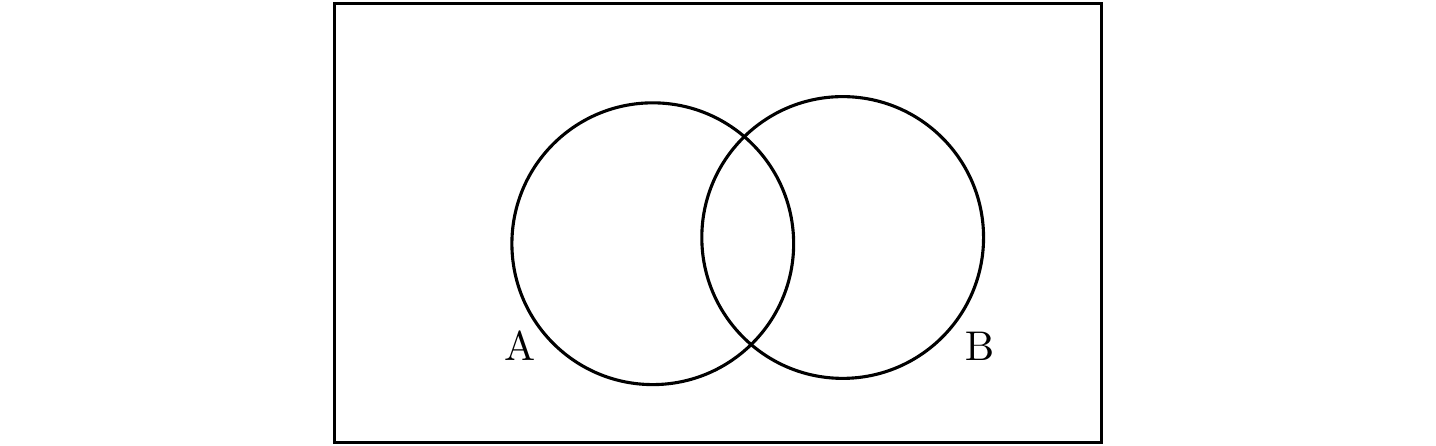
Figura 2.4: Polígono regular de 8 lados.
Prova. Devemos mostrar que um elemento que pertença a \(p\) dos conjuntos \(A_i\), para \(p=1,2,\ldots, n\), é contado pela Expressão (2.6) exatamente uma vez. Pertencendo a \(p\) dos conjuntos \(A_i\)`s, ele será contato \(p\) vezes em \[\sum_{i=1}^{n} |A_i|,\] em \[\sum_{1\leq i\leq j} |A_i \cap A_j|\] será contado \(C^2_p\) vezes (há \(C^2_n\) interseções dois a dois e o elemento está em \(C^2_p\) delas), em \[\sum_{1\leq i\leq j\leq k} |A_i \cap A_j \cap A_k|\] será contado \(C^3_p\) vezes, e assim sucessivamente até o termo \(|A_1 \cap A_2 \cap \cdots A_n|\), em que o elemento será contado uma vez. A interseção de mais do que \(p\) conjuntos não fornecerá nenhuma contribuição, pois o elemento em questão pertence a exatamente \(p\) dos conjuntos \(A_1, A_2, \ldots, A_n\).
Somando todas essas contribuições, teremos
\[\begin{equation} C^{1}_{p}-C^{2}_{p}+C^{3}_{p}-C^{4}_{p}+\cdots +(-1)^{p-1}C^{p}_{p}. \tag{2.7} \end{equation}\]
Os termos que aparecem na soma da Expressão (2.7) são os elementos da \(p\)-ésima linha do triângulo combinatório. Sabemos que termos equidistantes dos extremos em uma linha do triângulo combinatório são iguais \((C^{k}_{p}=C^{p-k}_{p})\), assim
\[C^{0}_{p}-C^{1}_{p}+C^{2}_{p}-C^{3}_{p}+C^{4}_{p}+\cdots +(-1)^{p}C^{p}_{p} = 0.\] Isso implica que a soma na Expressão (2.7) é igual a 1, pois \(C^{0}_{p}=1\).A seguir, veremos alguns exemplos de aplicação do Princípio da Inclusão e Exclusão.
Solução. Sejam \[\begin{align} A &= \{1, 2, 3, \ldots, 42000\}, \\ A_1 &= \{x \in A | x = 2k, k \in \mathbb{N}\}, \\ A_2 &= \{x \in A | x = 3k, k \in \mathbb{N}\}, \\ A_3 &= \{x \in A | x = 7k, k \in \mathbb{N}\}. \end{align}\]
Pelo Princípo da Inclusão e Exclusão, o número procurado será dado por \[\begin{align} |A| - |A_1\cup A_2 \cup A_3| = |A| &- |A_1| - |A_2| - |A_3| \\ &+ |A_1 \cap A_2| + |A_1 \cap A_3|+ |A_2 \cap A_3| \\ &- |A_1 \cap A_2 \cap A_3|. \end{align}\]
Como \[\begin{align} |A_1| &= \bigg\lfloor{\frac{4200}{2}}\bigg\rfloor=21000, &\quad |A_2| &= \bigg\lfloor{\frac{4200}{3}}\bigg\rfloor=14000, &\quad \\ |A_3| &= \bigg\lfloor{\frac{4200}{7}}\bigg\rfloor=6000, &\quad |A_1 \cap A_2| &= \bigg\lfloor{\frac{4200}{6}}\bigg\rfloor=7000, &\quad \\ |A_1 \cap A_3| &= \bigg\lfloor{\frac{4200}{14}}\bigg\rfloor=3000, &\quad |A_2 \cap A_3| &= \bigg\lfloor{\frac{4200}{21}}\bigg\rfloor=2000, &\quad\\ |A_1 \cap A_2 \cap A_3| &= \bigg\lfloor{\frac{4200}{42}}\bigg\rfloor=1000, &\quad |A| &= 42000, \end{align}\] temos que o número procurado é \(12000\).O Exemplo 2.23 abaixo é uma generalização do Exemplo 2.22.
Solução. Sejam \[\begin{align} A &= \{1, 2, 3, \ldots, m\}, \\ A_1 &= \{x \in A | x \text{ é divisível por } p_1\}, \\ A_2 &= \{x \in A | x \text{ é divisível por } p_2\}, \\ A_3 &= \{x \in A | x \text{ é divisível por } p_3\}, \\ &\vdots\\ A_r &= \{x \in A | x \text{ é divisível por } p_r\}. \\ \end{align}\]
Pelo Princípo da Inclusão e Exclusão, o número procurado será dado por \[\begin{align} |A| - |A_1\cup A_2 \cup \cdots \cup A_r| = |A| &- \sum_{i=1}^{r}|A_i| + \sum_{1\leq i<j}|A_i \cap A_j|\\ & + \sum_{1\leq i<j<k}|A_i \cap A_j \cap A_k|\\ & - \cdots + (-1)^r|A_1 \cap A_2 \cap\cdots\cap A_r|. \end{align}\]
Como \[\begin{align} |A| &= m, &\quad |A_i| &= \bigg\lfloor{\frac{m}{p_i}}\bigg\rfloor, &\quad \\ |A_i \cap A_j| &= \bigg\lfloor{\frac{m}{p_i p_j}}\bigg\rfloor, &\quad |A_i \cap A_j \cap A_k| &= \bigg\lfloor{\frac{m}{p_i p_j p_k}}\bigg\rfloor, \end{align}\] \[\begin{align} &\vdots \\ |A_1 \cap A_2 \cap\cdots\cap A_r| &= \bigg\lfloor{\frac{m}{p_1 p_2 \cdots p_r}}\bigg\rfloor \end{align}\]
Portanto, pelo Princípo da Inclusão e Exclusão, temos
\[\begin{align} |A| - |A_1\cup A_2 \cup \cdots \cup A_r| = m &- \sum_{i}\bigg\lfloor{\frac{m}{p_i}}\bigg\rfloor + \sum_{1\leq i < j}\bigg\lfloor{\frac{m}{p_i p_j}}\bigg\rfloor \\ &+ \cdots + (-1)^r\bigg\lfloor{\frac{m}{p_1 p_2 \cdots p_r}}\bigg\rfloor. \end{align}\]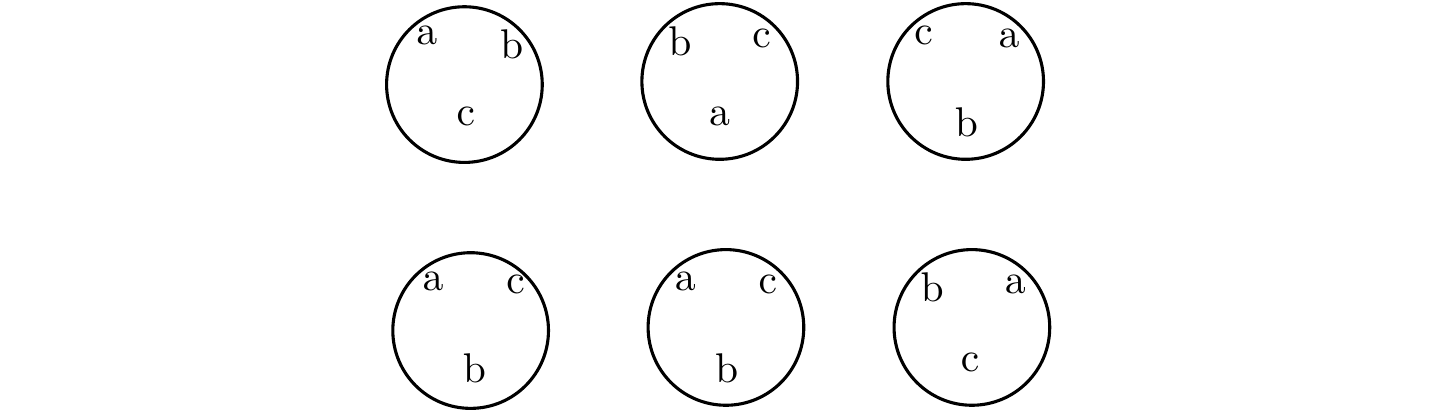
Figura 2.5: Permutação circular de três elementos.
Solução. Consideramos os casais \(C_i\), para \(i=1,\ldots, n\) e definimos os \(n\) conjuntos a seguir \(A_i =\) “conjunto das permutações circulares das \(2n\) pessoas nas quais os membros do \(i\)-ésimo casal estejam juntos”, para \(i=1,\ldots, n\). Estamos procurando o complementar da união destes \(n\) conjuntos. Veja que \(|A_i| = 2(2n-1-1)!\), pois o casal \(P_1,P_2\) pode se sentar de duas maneiras, a saber, \(P_1 P_2\) e \(P_2 P_1\), e, como estarão juntos na mesa circular, podem ser considerados como sendo uma única pessoa, sendo então \(2n-1\) elementos no círculo. Seguindo este mesmo raciocínio, \[\begin{align} |A_i \cap A_j| &= 2 \cdot 2 (2n - 2 -1)!, \\ |A_i \cap A_j \cap A_k| &= 2 \cdot 2 \cdot 2 (2n - 3 -1)!, \\ &\vdots \\ |A_i \cap A_j \cap \cdots \cap A_n| &= 2^n (2n - n -1)!. \end{align}\]
Então, \[\overline{A_i \cup A_j \cup \cdots \cup A_n} = (2n-1)! + \sum_{i=1}^{n}{n\choose i}(-1)^i2^i(2n-1-i)!.\]