Capítulo 1 Semana 1
1.1 Aula 1
Conjuntos
Existem duas maneiras de descrever um conjunto:
- Listar os elementos (quando possível);
- Através das propriedados do conjunto.
Exemplo 1.1
O conjunto das vogais: \(V = \{a, e, i, o, u\}\);
O conjunto dos inteiros positivos ímpares menores que 10: \(I = \{1,3,5,7,9\};\)
O conjunto dos inteiros positivos menores que 100: \(A = \{1,2,3,\ldots,99\}.\)
\(I = \{x\ |\ x,\) é inteiro, ímpar, positivo e menor que \(10 \} =\) \(\{x \in \mathbb{Z}^{+}|\) \(x \text{ é ímpar e }\) \(X < 10\}\).
O conjunto de todos os números racionais positivos: \(\mathbb{Q}^{+} =\) \(\{x \in \mathbb{R}|\) \(x = \frac{p}{q},\) \(\text{para alguns inteiros $p$ e $q$}\}.\)
Notação:
- \(\mathbb{N}\): conjunto dos números naturais;
- \(\mathbb{Z}\): conjunto dos números inteiros;
- \(\mathbb{Z}^{+}\): conjunto dos números inteiros positivos
- \(\mathbb{Q}=\big\{\frac{p}{q} \ | \ p \in \mathbb{Z}, q \in \mathbb{Z} \ \text{e} \ q \in \mathbb{Z} \big\}\): conjunto dos números racionais;
- \(\mathbb{R}\): conjunto dos números reais;
- \(\mathbb{R}^{+}\): conjunto dos números reais positivos;
- \(\emptyset\): conjunto vazio, não possui nenhum elemento.
Observação. \(A \subseteq B, \text{sse}, \forall a \in A \Rightarrow a \in B\).
para mostrar que \(A \nsubseteq B\), é necessário encontrar um elemento \(x \in A\), tal que \(x \notin B\).
para enfatizar que \(A\) é um subconjunto de \(B\), mas \(A \ne B\), escrevemos \(A \subset B\) (dizemos que \(A\) é subconjunto próprio de \(B\)).
- para mostrar que \(A = B\), devemos mostrar que \(A \subseteq B\) e \(B \subseteq A\).
Exemplo 1.3 A cardinalidade dos conjuntos definidos no Exemplo 1.1 é
\(|V| = 5\),
\(|I| = 5\),
\(|A| = 99\),
\(|\mathbb{Q}| = \infty\),
\(|\emptyset| = 0\).
Assita um vídeo explicativo vídeo aqui.
Exemplo 1.6 Considere \(\mathcal{S} = \{0,1,2\}\), então
\(\mathcal{P}(\mathcal{S}) = \{\emptyset, \{0\}, \{1\}, \{2\}, \{0,1\}, \{0,2\}, \{1,2\}, \underbrace{\{0,1,2\}}_{\mathcal{S}} \}.\)Observação. Se um conjunto tem \(n\) elementos, seu conjunto potência tem \(2^n\) elementos (este fato será provado adiante).
Exemplo 1.7 Sejam \(A = \{1,2\} \ \text{e} \ B = \{1,2,3\},\) então
\(A \times B = \{(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)\}.\)1.2 Aula 2
Operações entre conjuntos
Exemplo 1.8 Sejam \(A = \{1,3,5\} \ \text{e} \ B = \{1,2,3\}\), então
\(A \cup B = \{(1,2,3,5)\}.\)Exemplo 1.9 Sejam \(A = \{1,3,5\} \ \text{e} \ B = \{1,2,3\}\), então
\(A \cap B = \{(1,3)\}.\)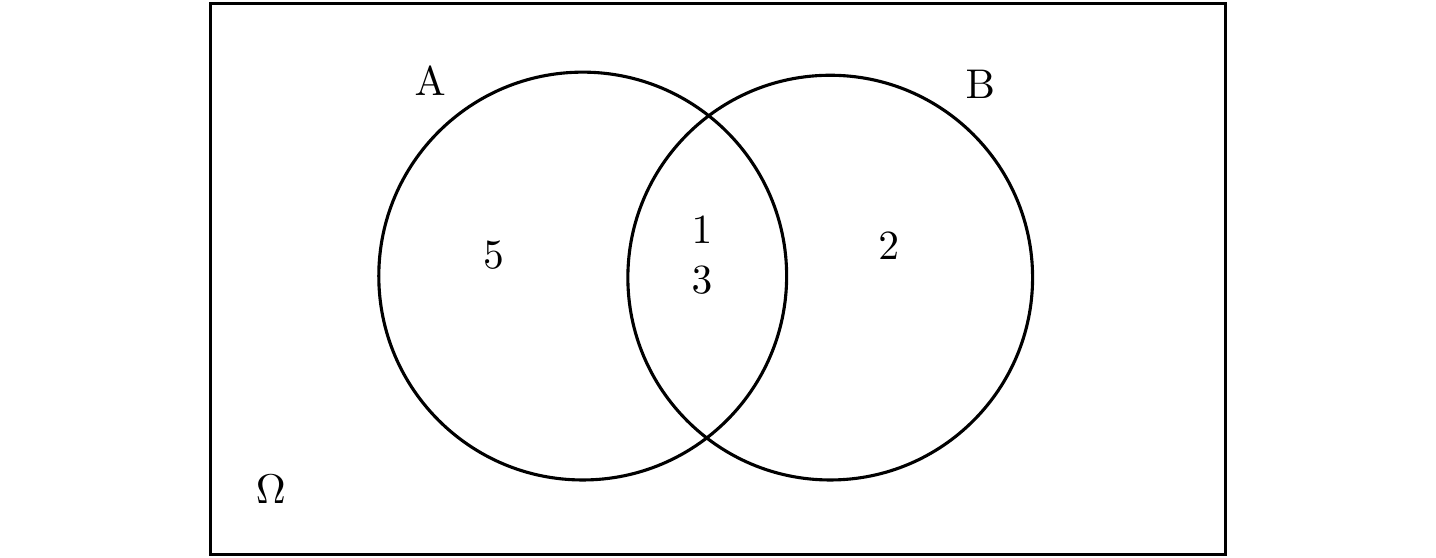
Figura 1.1: Diagrama de Venn que representa os conjuntos \(A\) e \(B\) dos exemplos anteriores.
Identidades de conjuntos
Solução. A ideia é mostrar que (i) \(\overline{A\cap B} \subseteq\) \(\overline A \cup \overline B\) e, depois, (ii) \(\overline A \cup\) \(\overline B \subseteq \overline{A\cap B}.\)
- Vamos mostrar que se \(x \in \overline{A\cap B} \Rightarrow\) \(x \in \overline A \cup \overline B.\)
\[\begin{align} x \in \overline{A\cap B} &\Rightarrow x \notin A\cap B \quad \text{(def. do complemento)}\\ & \Rightarrow \neg(x \in A\cap B) \quad \text{(def. de não pertencer)}\\ & \Rightarrow \neg(x \in A) \text{ ou } \neg(x \in B)\\ & \Rightarrow x \notin A \text{ ou } x \notin B\\ & \Rightarrow x \in \overline A \cup \overline B.\\ \end{align}\]
Ou seja, \(\overline{A\cap B} \subseteq\) \(\overline A \cup \overline B.\)
- Vamos mostrar que se \(x \in \overline A \cup \overline B \Rightarrow x \in \overline{A\cap B}.\) \[\begin{align} x \in \overline A \cup \overline B &\Rightarrow x \in \overline A \text{ ou } x \in \overline B \quad\text{(def. da união)}\\ & \Rightarrow x \notin A \text{ ou } x \notin B\quad\text{(def. do complemento)}\\ & \Rightarrow \neg(x \in A) \text{ ou } \neg(x \in B)\\ & \Rightarrow \neg(x \in A \text{ e } x \in B) \\ & \Rightarrow x \in \overline{A\cap B}.\\ \end{align}\]
1.3 Aula 3
Uniões e interseções gerais
Considere \(n\) conjuntos \(A_1, A_2, \ldots, A_n:\)
- sua união é \[\bigcup_{i=1}^{n}A_i = \{x: x \in A_i \text{ para algum $i$}\},\]
- sua interseção é \[\bigcap_{i=1}^{n}A_i = \{x: x \in A_i \text{ para todo $i$}\}.\]
Exemplo 1.11 Para \(i=1,2,\ldots,\) seja \(A_i=\{i, i+1, i+2, \ldots\}\), temos
\(\bigcup_{i=1}^{n}A_i =\) \(\bigcup_{i=1}^{n}\{i, i+1, i+2, \ldots\} =\) \(\{1,2,3,\ldots\}=\mathbb{Z}^+\),
- \(\bigcap_{i=1}^{n}A_i =\) \(\bigcap_{i=1}^{n}\{i, i+1, i+2, \ldots\} =\) \(\{n,n+1,n+2,\ldots\}=A_n\).
Observação. Podemos extender a notação anterior para um número enumerável de conjuntos, assim
\(A_1 \cup A_2 \cup \ldots \cup A_n \cup \ldots = \bigcup_{i=1}^{\infty}A_i,\)
\(A_1 \cap A_2 \cap \ldots \cap A_n \cap \ldots = \bigcap_{i=1}^{\infty}A_i,\)
Além disso, podemos generalizar a indexação do conjunto de índices. Considere novamente os conjuntos \(A_1, A_2, \ldots\) e seja \(I\) um conjunto, então
- \(\bigcup_{i\in I}A_i = \{x: \text{ existe } i\in I \text{ tal que } x \in A_i\},\)
- \(\bigcap_{i\in I}A_i = \{x: x \in A_i \text{ para todo $i \in I$}\}.\)
Exemplo 1.12 Seja \(A_i = \{1,2,\ldots, i\},\) \(i=1,2,3, \ldots\), então
\(\bigcup_{i=1}^{\infty}A_i = \bigcup_{i=1}^{\infty}\{1,2,\ldots, i\}=\{1,2,3,\ldots\}=\mathbb{Z}^+,\)
\(\bigcap_{i=1}^{\infty}A_i = \bigcap_{i=1}^{\infty}\{1,2,\ldots, i\}=\{1\}.\)
Representação de conjuntos na linguagem R
Se você não tem conhecimento prévio de R, veja o Apêndice A.
A linguagem R é bastante útil para manipulação de dados.
Podemos fazer todas as operações de conjuntos usando funções definidas na linguagem:
- função
union(A, B): \(A \cup B\); - função
intersect(A, B): \(A \cap B\); - função
setdiff(A, B): \(A \setminus B\);
Sejam \(A = \{1,2,3,4,5\}\), \(B=\{4,5,6,7\}\). A operação \(A \cup B\) então é obtida pelo comando
## [1] 1 2 3 4 5 6 7A operação \(A \cap B\) é obtida através comando
## [1] 4 5Finalmente, a operação \(A \setminus B\) pode ser feita usando
## [1] 1 2 3A utilização dessas funções em conjunto pode ser feita para obter operações mais complexas.
Somatórios e produtórios
Somas como \(a_k + a_{k+1} + \cdots + a_m\) podem ser escritas em forma compacta usando o símbolo somatório \(\big(\sum\big)\): \[\sum_{i=k}^{i=m}a_i=\sum_{i=k}^{m}a_i = a_k + a_{k+1} + \cdots + a_m.\]
Teorema 1.1 Seja \(n\) um inteiro qualquer, \(c\) um real qualquer e \(a_1, \ldots, a_n\), \(b_1, \ldots, b_n\) duas sequências de números. Então
- \(\sum_{i=1}^{n} c = nc,\)
- \(\sum_{i=1}^{n} ca_i = c\big(\sum_{i=1}^{n}a_i\big),\)
- \(\sum_{i=1}^{n} (a_i + b_i) = \sum_{i=1}^{n}a_i + \sum_{i=1}^{n}b_i\),
- \(\sum_{i=1}^{p}a_i + \sum_{i=p+1}^{n}a_i = \sum_{i=1}^{n}a_i,\)
- \(\sum_{i=0}^{n} a_{p-i}=\sum_{i=p-n}^{p} a_{i}.\)
O produto \(a_k\cdot a_{k+1}\cdots a_m\) é denotado por \(\prod_{i=k}^{m}a_i.\)
Teorema 1.2 Seja \(n\) um inteiro qualquer, \(c\) um real qualquer e \(a_1, \ldots, a_n\), \(b_1, \ldots, b_n\) duas sequências de números. Então
- \(\prod_{i=1}^{n}a_i b_i = \big(\prod_{i=1}^{n}a_i\big)\big(\prod_{i=1}^{n}b_i\big).\)
- \(\prod_{i=1}^{n} c = c^n.\)
- \(\prod_{i=1}^{n} ca_i = c^n\prod_{i=1}^{n}a_i.\)
- \(\prod_{i=1}^{n} a_i^2 = \big(\prod_{i=1}^{n}a_i\big)^2,\) em geral, \(\prod_{i=1}^{n} a_i^c = \big(\prod_{i=1}^{n}a_i\big)^c.\)
Exemplo 1.15 a. \[\begin{align} \prod_{i=1}^{3} i(i+1) &= (1\cdot 2)(2\cdot 3)(3\cdot 4) \\ &= (1\cdot 2\cdot 3)(2\cdot 3\cdot 4)\\ &= \bigg(\prod_{i=1}^{3}i\bigg)\bigg(\prod_{i=1}^{3}(i+1)\bigg). \end{align}\]
\(\prod_{i=1}^{3} 3i =\) \((3\cdot 1)(3\cdot 2)(3\cdot 3) =\) \(3^3\prod_{i=1}^{3}i.\)
\(\prod_{i=1}^{4}(i+1)^2 =\) \(2^2\cdot 3^2\cdot 4^2\cdot 5^2 =\) \((2\cdot 3\cdot 4\cdot 5)^2 =\) \(\big(\prod_{i=1}^{4}(i+1)\big)^2.\)
Somatórios e produtórios na linguagem R
Considere a soma \(\sum_{j=-2}^{3}j^2\) apresentada no Exemplo 1.13.
Duas formas de representá-la em R podem ser vistas abaixo, utilizando a função sum.
## [1] 19## [1] 19Caso tenha dúvidas em relação ao operador :, veja a Seção A.4.1.1.
Podemos utilizar a função prod para calcular produtórios.
Considere o produtório \(\prod_{i=1}^{3} 3i\) apresentado no Exemplo 1.15.
Veja como obtê-lo através de dois comandos no R:
## [1] 162## [1] 162Princípio de indução matemática
Este princípio é uma ferramenta útil para provar resultados envolvendo números inteiros.
Primeira forma do Princípio de Indução Matemática
Seja \(P(n)\) uma propriedade relativa aos inteiros. Se
\(P(n)\) é verdadeira para \(n=1\), e
\(P(k)\) é verdadeira e implica que \(P(k+1)\) é verdadeira,
então \(P(n)\) é verdadeira pra todo \(n \geq 1\).
Para aplicar a primeira forma do Princípio de Indução Matemática (PIM), devemos seguir os passos seguintes
Verificar se \(P(n)\) é verdadeira para \(n=1\) (passo inicial);
Assumir \(P(k)\) verdadeira (hipótese de indução) e provar que \(P(k+1)\) é verdadeira;
Se 1) e 2) valem, concluir que \(P(n)\) é válida para qualquer \(n \geq 1.\)
Solução. Vamos usar o PIM.
Passo inicial: para \(n=1\) \[\begin{align} 1^3 + (1+1)^3 + (1+2)^3 &= 1 + 8 + 27\\ &= 36 \\ &= 9 \cdot 4. \end{align}\]
Hipótese de indução: para \(n=k\), \[k^3 + (k+1)^3 + (k+2)^3 = 9L,\] em que \(L\) é um inteiro. Devemos mostrar que \[(k+1)^3 + [(k+1) + 1]^3 + [(k+1)+2]^3 = 9M,\] para algum inteiro \(M\). \[\begin{align} (k+1)^3 + [(k+1) + 1]^3 + [(k+1)+2]^3 &= (k+1)^3 + (k+2)^3 + (k+3)^3\\ &= (k+1)^3 + (k+2)^3 + (k^3 + 3k^2 3 + 3k9 + 27)\\ &= \underbrace{(k+1)^3 + (k+2)^3 + k^3}_{9L} + 9K^2 + 27k + 27\\ &= 9L + 9k^2 + 27k + 27\\ &= 9(L + k^2 + 3k + 3)\\ &= 9M, \end{align}\] em que \(M = L + 3k^2 + 3k + 3.\)
Solução. As primeiras cinco somas são tais que \[\begin{align} 1 &= 1^2 \\ 1 + 3 = 4 &= 2^2\\ 1 + 3 + 5 = 9 &= 3^2\\ 1 + 3 + 5 + 7 = 16 &= 4^2\\ 1 + 3 + 5 + 7 + 9 = 25 &= 5^2. \end{align}\]
Portanto, a conjectura é \(\sum_{i=1}^{n}(2i-1)=n^2.\) Vamos usar o princípio de indução matemática para prová-la.
Passo inicial: \(n=1\) \[\sum_{i=1}^{1}(2i-1) = 1 = 1^2.\]
Hipótese de indução: supor que vale para \(n=k\). Considere a soma para \(n=k+1\) \[\begin{align} \sum_{i=1}^{k+1}(2i-1) &= \sum_{i=1}^{k}(2i-1) + [2(k+1)-1]\\ &= k^2 + 2k + 1 \\ &= (k+1)^2. \end{align}\]
Solução. 1. Passo inicial: \(\prod_{i=1}^{1}a_i^m = a_1^m = \bigg(\prod_{i=1}^{1}a_i\bigg)^m.\)
- Hipótese de indução: supor que vale para \(n=k.\) \[\prod_{i=1}^{k}a_i^m = \bigg(\prod_{i=1}^{k}a_i\bigg)^m.\] Assim, \[\begin{align} \prod_{i=1}^{k+1}a_i^m &= \bigg(\prod_{i=1}^{k}a_i^m\bigg) \bigg(\prod_{i=k+1}^{k+1}a_i^m\bigg) \\ &=\bigg(\prod_{i=1}^{k}a_i\bigg)^m a_{k+1}^{m} \\ &= \bigg[\bigg(\prod_{i=1}^{k}a_i\bigg)a_{k+1}\bigg]^m\\ &= \bigg(\prod_{i=1}^{k+1}a_i\bigg)^m. \end{align}\]
1.4 Aula 4
Segunda forma do princípio de Indução Matemática
Seja \(P(n)\) uma propriedade relativa aos inteiros. Se
- \(P(n)\) é verdadeira para \(n=1\) e
- \(P(n)\) é verdadeira para \(1\leq n \leq k\) e implica que \(P(k+1)\) é verdadeira, então \(P(n)\) é verdadeira para todo inteiro \(n \geq 1.\)
Solução.
Temos que \(2^1 + (-1)^1 =\) \(1 = \mu(1)\) e \(2^2+(-1)^2=5=\) \(\mu(2),\) portanto \(p(1)\) e \(p(2)\) são verdadeiras.
Supor que, para todo inteiro \(n\) tal que \(2 < n \leq k\) a equação \(\mu(n) = \mu(n-1) + 2\mu(n-2)\) é válida. Devemos provar que a equação é válida para \(n=k+1\). Assim,
\[\begin{align} \mu(k+1) &= \mu(k) + 2\mu(k-1)\\ &= 2^k + (-1)^k + 2[2^{k-1} + (-1)^{k-1}]\\ &= 2\cdot 2^k + (-1)^k + 2(-1)^{k-1}\\ &= 2^{k+1} + (-1)^{k-1}[(-1)+2]\\ &= 2^{k+1} + (-1)^{k-1}[1] \qquad{\text{(note que $(-1)^{k-1}=(-1)^{k+1}$})}\\ &= 2^{k+1} + (-1)^{k+1}. \end{align}\]
Dessa forma, com \(P(1)\), \(P(2)\), \(\ldots\), \(P(k)\) são válidas, então \(P(k+1)\) também é.
Solução.
Temos que \(P(0)\) é verdadeiro, i.e., o conjunto vazio tem \(2^0=1\) subconjunto.
Supor verdadeiro para \(n=k\), ou seja, todo conjunto com \(k\) elementos tem \(2^k\) subconjuntos. Vamos mostrar que vale para \(n=k+1.\) Seja \(\mathcal{T}\) um conjunto com \(k+1\) elementos. Então, podemos escrever \[\mathcal{T} = \mathcal{S}\cup\{a\},\] em que \(a \in \mathcal{T}\) e \(\mathcal{S}=\mathcal{T}\setminus\{a\},\) assim, \(|\mathcal{S}|=k.\) Os subconjuntos de \(\mathcal{T}\) podem ser obtidos da seguinte forma: para cada subconjunto \(\mathcal{X}\) de \(\mathcal{S}\), existem dois subconjuntos de \(\mathcal{T}\), a saber, \(\mathcal{X}\) e \(\mathcal{X}\cup \{a\}.\) Veja na figura 1.2. Essa abordagem inclui todos os subconjuntos de \(\mathcal{T}\), e são todos distintos. Vamos agora usar a hipótese de indução. \(\mathcal{S}\) tem \(2^k\) subconjuntos, pois tem \(k\) elementos. Também sabemos que existem 2 subconjuntos de \(\mathcal{T}\) para cada subconjunto de \(\mathcal{S}\). Então, temos \(2\cdot 2^k = 2^{k+1}\) subconjuntos de \(\mathcal{T}.\)
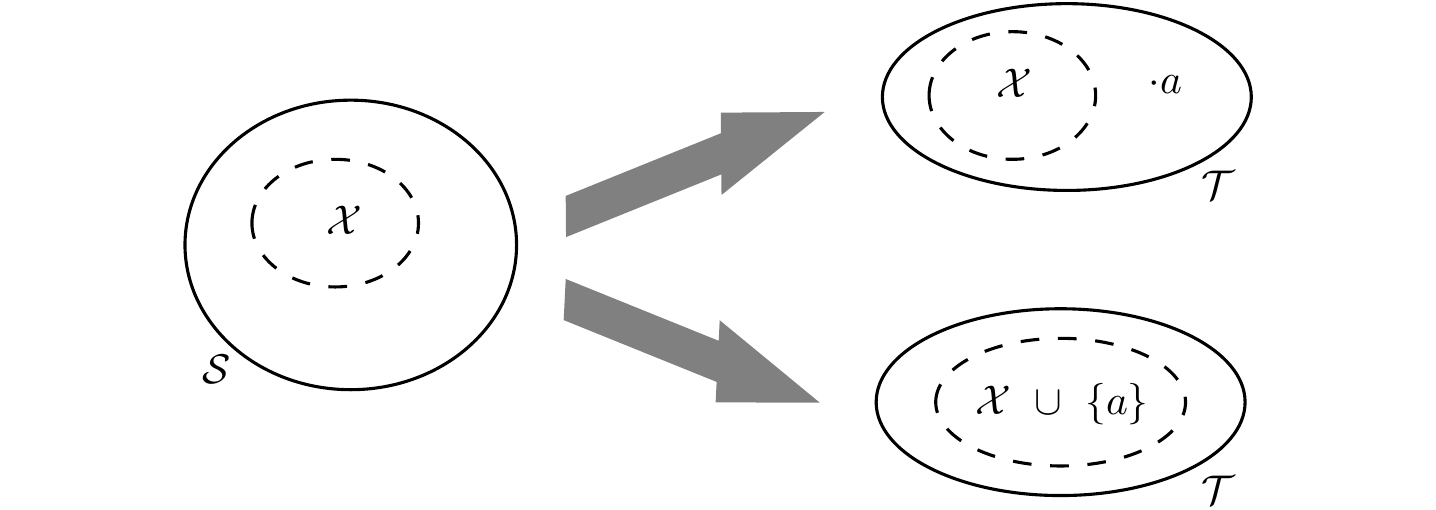
Figura 1.2: Decomposição do conjunto.
1.5 Aula 5
Princípio aditivo e multiplicativo
Extensão do princípio aditivo
Se \(A_1, A_2, \ldots, A_n\) são conjuntos, disjuntos 2 a 2, e se \(A_i\) possui \(a_i\) elementos, então a união \(\bigcup_{i=1}^{n}A_i\) possui \(\sum_{i=1}^{n}a_i\) elementos.
Extensão do princípio multiplicativo
Se um evento \(A_i\) pode ocorrer de \(m_i\) maneiras diferentes, \(i = 1,2,\ldots, n\), então esses \(n\) eventos podem ocorrer, em sucessão, de \(m_1 \times m_2 \times \cdots \times m_n\) maneiras diferentes.
Em linguagem de conjuntos, se \(A_1, A_2, \ldots, A_n\) são conjuntos finitos com \(|A_i|=m_i\), \(i = 1,2,\ldots, n\), então, se \(A_i \cap A_j = \emptyset\), \(i \neq j\), \[ |A_1 \cup A_2 \cup \cdots \cup A_n| = \sum_{i=1}^{n}|A_i|,\] \[ |A_1 \times A_2 \times \cdots \times A_n| = \prod_{i=1}^{n}|A_i|.\]
Aplicações dos Princípios Aditivo e Multiplicativo
Solução. Posso fazer as seguintes escolhas:
\[ \left.\begin{array}{ll} \text{a)}& \text{Matemática e física: } 5 \times 7 = 35 \text{ maneiras;} \\ \text{b)}& \text{Matemática e química: } 5 \times 10 = 50 \text{ maneiras;} \\ \text{c)}& \text{Física e química: } 7 \times 10 = 70 \text{ maneiras.} \end{array}\right\} \text{(princípio multiplicativo)} \]
Como minhas escolhas só podem ocorrer dentre uma das possibilidades a), b) ou c), então, pelo princípio aditivo, \(35 + 50 + 70 = 155\) é o número de maneiras de fazer essas escolhas.Solução.
- Considerando as 3 mulheres que possuem irmãos (2), ha \(3\times 8=24\) casamentos possíveis;
- Considerando as 9 mulheres que não possuem irmãos, há \(9\times 10=90\) casamentos possíveis;
portanto, pelo princípio aditivo, há \(24+90 = 114\) casamentos heterosexuais possíveis.