Manufacturer's pallet loading problem

• This problem consists on arranging (orthogonally and without overlapping) the maximum number of identical rectangles into a large rectangle.
  
  

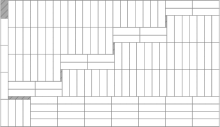
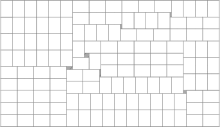
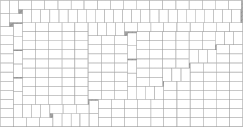
  E. G. Birgin, R. D. Lobato and R. Morabito, "An effective recursive partitioning approach for the packing of identical rectangles in a rectangle", Journal of the Operational Research Society 61, pp. 306-320, 2010. [Abstract] [pdf] [ps] [Website and code]

  E. G. Birgin, R. Morabito and F. H. Nishihara "A note on an L-approach for solving the manufacturer's pallet loading problem", Journal of the Operational Research Society 56, pp. 1448-1451, 2005. [Abstract] [pdf] [ps]

Distributor's pallet loading problem

• This problem consists of cutting different types of rectangular pieces from a rectangular plate.
  
  

  E. G. Birgin, R. D. Lobato and R. Morabito, "Generating unconstrained two-dimensional non-guillotine cutting patterns by a recursive partitioning algorithm", submitted, 2010. [Abstract] [pdf] [Website]

Packing circles and spheres by Nonlinear Optimization

We considered several packing problems using nonlinear programming models:

• Minimizing the object dimensions in circle and sphere packing problems:
  
  

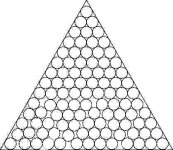
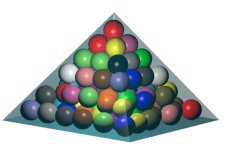
  E. G. Birgin and F. N. C. Sobral, "Minimizing the object dimensions in circle and sphere packing problems", Computers & Operations Research 35, pp. 2357-2375, 2008. [Abstract] [pdf] [ps] [Website and code]

  E. G. Birgin and J. M. Gentil, "New and improved results for packing identical unitary radius circles within triangles, rectangles and strips", Computers & Operations Research 37, pp. 1318-1327, 2010. [Abstract] [pdf] [Website and code]

• Packing of the maximum number of identical circles within circular and rectangular regions:
  
  

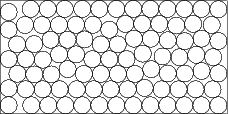
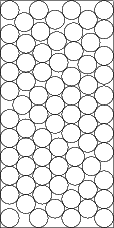
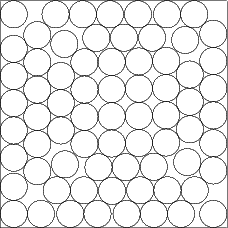
  E. G. Birgin, J. M. Martínez and D. P. Ronconi, "Optimizing the Packing of Cylinders into a Rectangular Container: A Nonlinear Approach", European Journal of Operational Research 160, pp. 19-33, 2005. [Abstract] [pdf] [ps] [Code]

Packing rectangles within arbitrary convex regions by Nonlinear Optimization

We considered several packing problems using nonlinear programming models:

• Packing of the maximum number of rectangular items within arbitrary convex regions:
  
  

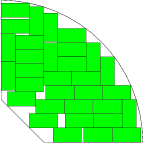
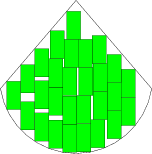
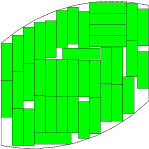
  E. G. Birgin and R. D. Lobato, "Orthogonal packing of identical rectangles within isotropic convex regions", Computers & Industrial Engineering 59, pp. 595-602, 2010. [Abstract] [pdf] [Code]

  E. G. Birgin, J. M. Martínez, F. H. Nishihara and D. P. Ronconi, "Orthogonal packing of rectangular items within arbitrary convex regions by nonlinear optimization", Computers & Operations Research 33, pp. 3535-3548, 2006. [Abstract] [pdf] [ps] [Code]

• Packing of the maximum number of free-rotated rectangular (and arbitrary polygonal) items within arbitrary convex regions:
  
  

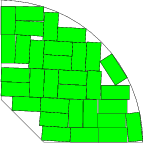
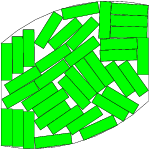
  E. G.Birgin, J. M. Martínez, W. F. Mascarenhas and D. P. Ronconi "Method of Sentinels for Packing Items whitin Arbitrary Convex Regions", Journal of the Operational Research Society 57, pp. 735-746, 2006. [Abstract] [pdf] [ps].

  W. F. Mascarenhas and E. G. Birgin, "Using sentinels to detect intersections of convex and nonconvex polygons", Computational & Applied Mathematics 29, pp. 247-267, 2010. [Abstract] [pdf] [ps]