 |
Packing Circles and Spheres using Nonlinear Programming |
Introduction
Given a fixed set of identical or different-sized circular items, the problem consists on finding the smallest object within which the items can be packed. As smallest object, we consider the object which has the smallest area, perimeter, volume or surface area, depending on the object and the problem dimension.
This page shows numerical results and visual solutions for the problems considered in:
E. G. Birgin and F. N. C. Sobral, Minimizing the object dimensions in circle and sphere packing problems, Computers & Operations Research 35, pp. 2357-2375, 2008. [Abstract] [pdf] [ps]
Unitary-radius circles
The objects considered here are: circle, square, strip, equilateral triangle and rectangle.
| Packing of unitary-radius circles in a circle | Numerical results and graphics | [source] |
| Packing of unitary-radius circles in a rectangle (minimizing area) | Numerical results and graphics | [source] |
| Packing of unitary-radius circles in a rectangle (minimizing perimeter) | Numerical results and graphics | [source] |
| Packing of unitary-radius circles in a square | Numerical results and graphics | [source] |
| Packing of unitary-radius circles in a strip | Numerical results and graphics | [source] |
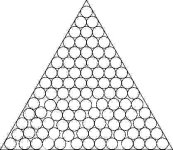
| Packing of unitary-radius circles in an equilateral triangle | Numerical results and graphics | [source] |
Explanation of the filesThe .dat files contain all the information about the desired problem and the coodinates of the spheres for the final packing which includes all the information in the tables and the solution coordinates for each circle. The .mp files are MetaPost files. To visualize the solutions, just follow the following steps. In a linux shell, type |
 |
mp desired-file.mp
A file named desired-file.1 (an EPS file) will be created. Rename it to figure.1. Now you have to include this recently created file into a Tex file. Download the file figures.tex. Then type
latex figures.tex dvips figures.dvi -o figures.ps
Now type
gv figures.ps
to see the desired solution.
Unitary-radius spheres
The objects considered here are: cube, cuboid, cylinder, pyramid, regular tetrahedron, sphere and 3D strip.
| Packing of unitary-radius spheres in a cuboid (minimizing volume) | Numerical results and graphics | [source] |
| Packing of unitary-radius spheres in a cuboid (minimizing surface) | Numerical results and graphics | [source] |
| Packing of unitary-radius spheres in a cube | Numerical results and graphics | [source] |
| Packing of unitary-radius spheres in a cylinder (minimizing volume) | Numerical results and graphics | [source] |
| Packing of unitary-radius spheres in a cylinder (minimizing surface) | Numerical results and graphics | [source] |
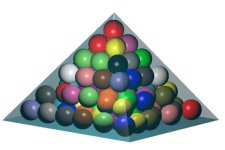
| Packing of unitary-radius spheres in a squared pyramid | Numerical results and graphics | [source] |
| Packing of unitary-radius spheres in a sphere | Numerical results and graphics | [source] |
| Packing of unitary-radius spheres in a 3D strip | Numerical results and graphics | [source] |
| Packing of unitary-radius spheres in a regular tetrahedron | Numerical results and graphics | [source] |
Explanation of the filesThe .dat files contain all the information about the desired problem and the coodinates of the spheres for the final packing which includes all the information in the tables and the solution coordinates for each sphere. The .vmd files are batch files to be ran on the VMD - Visual Molecular Dinamics shell. In order to visualize the solution you have to install VMD, open it and, on the shell, type: |
 |
play desired-file.vmd
