|
Alguns exemplos em SCILAB
Aqui estăo alguns scripts e funçőes simples em SCILAB para entender
como funcionam.Para rodar os scripts: exec("nome_arquivo.sce") Para usar as funçőes getf("nome_funcao.sci")
13 de March de 2008 |
|
O método da bissecçăo no SCILAB
O seguinte código é da funçăo bissec1.sci
para o SCILAB. Para usá-la:
function [raiz,iter]=bissec1(f,a,b,eps1), //calcula a raiz de f(x) no intervalo [a,b] // com precisăo eps1 x0=a; x1=b; xm=(x0+x1)./2; it=0; while (min(abs(f(xm)),(x1-x0))>eps1)&it<=150 do if f(x0).*f(xm) > 0 then x0=xm; else x1=xm; end; xm=(x0+x1)./2; it=it+1; end; raiz=xm; iter=it; endfunction; 11 de March de 2008 |
|
Resumo da quarta aula
Polinômios de Taylor: Uma forma importante para aproximar
funçőes, ou avaliar funçőes em pontos próximos de pontos em que
conhecemos o valor da funçăo é usar o teorema de Taylor.Se $f: I \to \mathbb{R}$ é uma funçăo de classe $\mathcal{C}^{n+1}$ no intervalo $I$ e se $x$ e $c$ săo pontos no interior do intervalo entăo \[f(x)=f(c)+f^\prime(c)(x-c)+\cdots + f^{(n)}(c)\frac{(x-c)^n}{n!} + R_n(x)\] onde o resto $R_n$ pode ser escrito
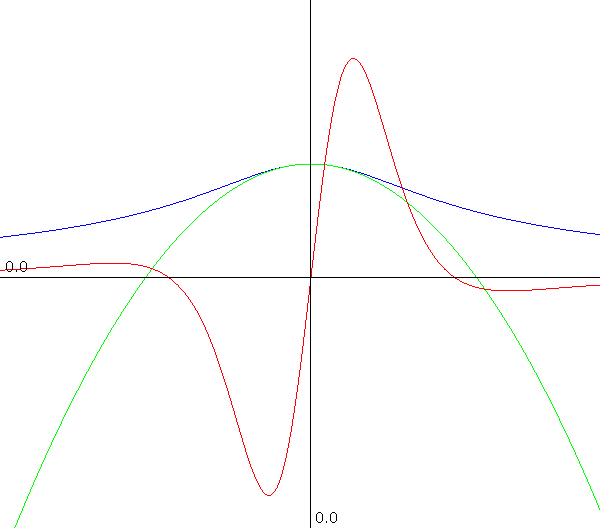
Seja $f(x) = 1/\sqrt{x^2+1}$. Vamos calcular o polinomio de Taylor de ordem 2 centrado no zero. Teremos: $f(0) = 1$, $f^\prime(0)=0$ e $f^{\prime\prime}(0)=-1$. Entăo temos $p_2(x)=1-x^2/2$. na figura abaixo o polinômio de taylor está em azul. Em vermelho temos o gráfico da terceira derivada da funçăo. O valor máximo da terceira derivada é $2$. 08 de March de 2008 |
|
Resumo da terceira aula
O conjunto dos números de máquina $M$ é um conjunto finito e
$\text{fl} : \mathbb{R} \to M$ é um processo de arredondamento usado pela máquina. Se a representaçăo na forma normal em ponto flutuante de um número $x$ é
$x= m*B^e$ entăo os erros absoluto e relativo entre $x$ e $\text{fl}(x)$ podem
ser estimados como
\[ |x-\text{fl}(x)| \leq 0.5*|\bar{m} - \hat{m}|*B^e \]
e
\[\frac{|x-\text{fl}(x)|}{|x|} \leq 0.5*|\bar{m} - \hat{m}|*B^e\]
onde $\bar{m}$ é o truncamento da mantissa de $m$ e $\hat{m}$ é o arredondamento por excesso de $m$.
Para a aritmética de pontos flutuantes năo valem as propriedades associativas e distributivas. Neste caso $x\oplus y = \text{fl}(\text{fl}(x) + \text{fl}(y))$.
Estes erros de arredondamentos acabam se propagando. Vimos também um exemplo de perda de algarismos significativos ( ou seja aumento de erro relativo) no caso de subtraçăo de dois números muito próximos.05 de March de 2008 |
|
Introduçăo ao Scilab em portuguęs
O professor Paulo Sérgio da Motta Pires escreveu este
Manual em portuguęs do Scilab 01 de March de 2008 |
|
Epsilon da Máquina
É o menor número de máquina. O seguinte algorítmo calcula o epsilon de
máquina com precisăo duplaeps.c
#include <stdio.h>
main (){
double s;
double t;
int k;
s=1.0;
t=1;
for (k=1;k<= 100; k++) {
s=0.5*s;
t=1.0+s;
if (t<=1.0) {
printf(" Epsilon = %E\n ", 2*s);
break;}}
}
Generated by GNU enscript 1.6.4. 01 de March de 2008 |