Este capítulo resolve o problema do emparelhamento máximo em grafos não-dirigidos. O algoritmo para o problema constrói um emparelhamentos máximo costurando emparelhamentos perfeitos — veja o capítulo 7 — em subgrafos do grafo dado.
Todos os grafos neste capítulo serão não-dirigidos. Por isso, diremos simplesmente grafo, deixando subentendido o adjetivo não-dirigido. Muitos dos conceitos usados neste capítulo foram definidos no capítulo 6 e no capítulo 7. Para as definições de outros termos técnicos, consulte o índice remissivo e os apêndices.
Um emparelhamento $M$ num grafo é máximo se $|M| \geq |M'|$ para qualquer outro emparelhamento $M'$. É claro que um emparelhamento é máximo se e somente se minimiza o número de nós expostos. Eis o problema central deste capítulo:
Problema 8.A (do emparelhamento máximo) Encontrar um emparelhamento máximo num grafo.
O capítulo 6 fez algumas observações preliminares sobre o problema e introduziu uma técnica dos caminhos de aumento para lidar com o problema.
Denota-se por $\nu(G)$ a cardinalidade de um emparelhamento máximo no grafo $G$. [Não confunda a letra $\nu$ com a letra $v$.] Denota-se por $\df(G)$ o número de nós expostos por um emparelhamento máximo. Esse número é conhecido como deficiência de $G$. Evidentemente \begin{equation}\label{eq:df-versus-nu} \df(G) = |V|-2\nu(G)\text{.} \end{equation}
Se $G$ tem um emparelhamento perfeito, por exemplo, então $\nu(G) = \frac{1}{2}|V(G)|$ e $\df(G) = 0$.
A restrição do problema 8.A a grafos bipartidos já foi resolvida na seção 6.5. O capítulo 7 tratou do caso especial do problema 8.A em que o emparelhamento máximo é perfeito. Este capítulo usa as soluções dos casos especiais para resolver o problema 8.A em geral.
Como podemos certificar a maximalidade de um dado emparelhamento máximo $M$? Que objeto podemos exibir para tornar evidente que $M$ é máximo?
De acordo com o lema 6.2 da seção 6.4, temos $|M| \leq |K|$ para todo emparelhamento $M$ e toda cobertura $K$. Portanto, uma cobertura $K$ tal que $|K| = |M|$ é um certificado da maximalidade de $M$. Infelizmente, muitos grafos não têm uma cobertura tão pequena. Uma delimitação superior mais forte decorre do lema 7.2 da seção 7.2, que introduziu a condição de Tutte:
Lema 8.1 (das componentes ímpares) Para qualquer emparelhamento $M$ e qualquer subconjunto próprio $A$ de $V$, tem-se \[\textstyle |M| \ \leq \ \frac{1}{2} \big(|V| - \oc(G{-}A) + |A|\big)\text{,} \] ou seja, $|V|-2|M| \geq \oc(G{-}A) - |A|$, onde $V$ é o conjunto de nós de $G$.
Aqui, como na seção 7.2, $\oc(G{-}A)$ é o número de componentes ímpares do subgrafo de $G$ induzido por $V\setm A$.
Prova do lema:
Seja $k:=\oc(G{-}A)$ e
sejam $H_1,\ldots,H_k$ as componentes ímpares de $G{-} A$.
Para cada $i$,
seja $V_i:=V(H_i)$,
$E_i:=E(H_i)$ e $M_i:= M\cap E_i$.
Como $|V_i|$ é ímpar, temos $2|M_i|\leq |V_i| - 1$.
Logo,
cada grafo $H_i$ tem um nó $v$ que é especial
no seguinte sentido:
$v$ está exposto por $M$
ou está ligado a $A$ por alguma aresta de $M$.
Por outro lado,
no máximo $|A|$ arestas de $M$ têm uma ponta em $A$.
Portanto, pelo menos $k-|A|$ nós especiais
estão expostos.
Em outras palavras, $|V|-2|M| \geq k-|A|$. ■
Ocasionalmente usaremos a expressão $\sz{A}$ para denotar o número $\frac{1}{2} (|V| - \oc(G{-}A) + |A|)$. Com essa notação, a conclusão do lema pode ser escrita assim: $|M| \leq \sz{A}$.
Exemplo 8.1: Suponha que $K$ é uma cobertura de $G$, Observe que $\oc(G-K)=|V|-|K|$. Por outro lado, $\sz{K} = \text{}$ $\frac{1}{2}(|V| - (|V|-|K|) + |K|) = |K|$. Segue daí que $\min^{}_{A\subset V} \sz{A} \leq \text{}$ $\sz{K} = |K|$. Isso mostra que a cota superior $|K|$ é mais fraca que a cota superior $\sz{A}$ dada pelo lema 8.1.
Exemplo 8.2: Se $G$ é um circuito de comprimento $2k+1$ e nada mais então $\min_{A\subset V} \sz{A} = k$. Com efeito, como $G$ tem um emparelhamento com $k$ arestas, o lema 8.1 garante que $k \leq \sz{A}$ para todo $A\subset V$. Por outro lado, $\min_{A} \sz{A} \leq \sz{\emptyset} = \frac{1}{2} (|V| - \oc(G)) = \frac{1}{2} (2k+1 - 1) = k$.
O lema 8.1 tem a seguinte consequência: para provar que um dado emparelhamento $M$ é máximo, basta exibir um conjunto $A$ de nós tal que $|V|-2|M| = \oc(G{-}A) - |A|$. Um tal conjunto $A$ serve de certificado de maximalidade do emparelhamento.
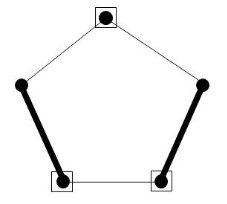
Exemplo 8.3: Seja $G$ o grafo da figura e $A$ o conjunto dos três nós brancos. Observe que $G{-}A$ tem $6$ componentes conexas: duas têm $1$ nó cada, uma tem $2$ nós, duas têm $3$ nós cada, e uma tem $5$ nós. Portanto, $\oc(G{-}A)= 5$.
Seja $M$ o emparelhamento com $8$ arestas indicado pelas linhas mais grossas e observe que $|V|- 2|M| = \text{}$ $18-2\times 8 = \text{}$ $5 - 3 = \oc(G{-}A) - |A|$. Portanto, $|M| = \sz{A}$. Em virtude do lema 8.1, o emparelhamento $M$ é máximo. [CCPS fig.5.1]
W. Tutte e C. Berge mostraram (1947 e 1958) que a delimitação superior dada pelo lema 8.1 é justa:
Teorema 8.2 (de Tutte–Berge) Todo grafo $G$ tem um emparelhamento $M$ e um subconjunto próprio $A$ de $V$ tais que \[\textstyle |M| \ = \ \frac{1}{2} \big(|V| - \oc(G{-}A) + |A|\big)\text{,} \] ou seja, tais que $|V|-2|M| = \oc(G{-}A) - |A|$, onde $V$ é o conjunto de nós de $G$.
A próxima seção mostra uma prova algorítmica do teorema. Uma seção subsequente dá uma prova não algorítmica. A combinação do teorema 8.2 com o lema 8.1 leva à seguinte fórmula de Tutte–Berge: em qualquer grafo $G$, \begin{equation}\label{eq:tutte-berge-formula} \max_M\,|M| \ = \ \min_A\, {\textstyle\frac{1}{2}} \big(|V| - \oc(G{-}A) + |A|\big)\text{,} \end{equation} onde $\max_M$ é tomado sobre todos os emparelhamentos $M$ e $\min_A$ é tomado sobre todos os subconjuntos próprios $A$ de $V$. Com a notação que introduzimos acima, essa fórmula pode também ser escrita assim: \[ \max_M\,|M| \ = \ \min_A\, \sz{A}\text{.} \]
É fácil ver que o teorema 7.3 (teorema de Tutte para emparelhamentos perfeitos) decorre do teorema 8.2. Surpreendentemente, a recíproca é verdadeira: o teorema 8.2 decorre do teorema 7.3. Os dois teoremas são, portanto, equivalentes.
Um emparelhamentos máximo em um grafo $G$
pode ser obtido costurando
emparelhamentos perfeitos
em subgrafos de $G$.
Assim, nosso algoritmo
para o problema 8.A
tem o caráter de uma colcha de retalhos:
ele constrói um emparelhamento máximo
reunindo os emparelhamentos
que o algoritmo EmpPerfeito
da seção 7.6
produz ao tentar obter emparelhamentos perfeitos
em sucessivas fatias
de $G$.
Para fazer uma introdução suave ao algoritmo, começamos por examinar a versão do algoritmo para grafos bipartidos.
Dado um grafo bipartido $G$, queremos encontrar um emparelhamento $M$ e uma cobertura $A$ dos nós de $G$ tais que \begin{equation*} |M|=|A|\text{.} \end{equation*} Segundo o lema 6.2 do capítulo 6, um tal emparelhamento é máximo.
O algoritmo é recursivo. Comece por submeter $G$ ao algoritmo EmpBipartidoPerfeito (seção 7.4). Supoha inicialmente que a execução do algoritmo termina na linha 13 e devolve um emparelhamento perfeito $M$. Seja $A$ um dos lados de uma bipartição de $G$. Então $A$ é uma cobertura de $G$ e $|M|=|A|$, como desejamos. Esse caso está na base da recursão.
Suponha agora que a execução do algoritmo EmpBipartidoPerfeito termina na linha 10 com uma árvore frustrada $T$ (veja a seção 7.3). Seja $V_1$ o conjunto de nós de $T$, seja $M_1$ o emparelhamento $M\cap E(T)$, seja $A_1$ o conjunto de nós brancos de $T$ e seja $B_1$ o conjunto de nós pretos de $T$. Observe que $A_1\cup B_1=V_1$, que $|B_1| = |A_1|+1$, que toda aresta de $G$ com uma ponta em $B_1$ tem a outra em $A_1$ e que $M_1$ deixa exatamente um nó exposto no grafo induzido $G[V_1]$. Segue daí que $A_1$ é uma cobertura de $G[V_1]$ e que nenhuma aresta de $G$ liga $B_1$ ao conjunto $V(G)\setm V_1$. Segue daí também que $\oc(G[V_1]{-}A_1) - |A_1| = \text{}$ $|B_1|-|A_1| = \text{}$ $1$ e que $|V_1|-2|M_1| = 1$, donde $|M_1|= |A_1|$.
Se $V_1=V(G)$ então a recursão terminou, pois o par $(M_1,A_1)$ tem as propriedades desejadas. Suponha agora que $V_1\neq V(G)$. Aplique o algoritmo que estamos descrevendo ao grafo $G-V_1$. Isso produzirá um emparelhamento $M_2$ e uma cobertura $A_2$ de $G-V_1$ tais que $|M_2|=|A_2|$. Logo, $M_1\cup M_2$ é um emparelhamento em $G$, $A_1\cup A_2$ é uma cobertura de $G$, e $|M_1\cup M_2| = \text{}$ $|A_1\cup A_2|$, como desejamos.
O algoritmo que acabamos de descrever equivale ao algoritmo baseado em fluxo máximo que foi discutido na seção 6.5.
Exemplo 8.4: Seja $G$ o grafo bipartido representado na figura. Começamos por submeter $G$ ao algoritmo EmpBipartidoPerfeito. As primeiras quatro iterações encontram o emparelhamento $\conj{\textcolor{blood}{bd},\textcolor{blood}{ce}, \textcolor{blood}{ih},\textcolor{blood}{jg}}$.
A quinta iteração constrói uma árvore alternante a partir do nó exposto $a$. A execução do algoritmo termina na linha 10 e devolve os conjuntos descritos a seguir. Observe que $M_1$ é um emparelhamento em $G[V_1]$, $A_1$ é uma cobertura de $G[V_1]$, e $|M_1|=|A_1|$.
A segunda execução de EmpBipartidoPerfeito processa o grafo $G-V_1$. O algoritmo constrói uma árvore alternante a partir do nó exposto $f$ e termina na linha 10 devolvendo os conjuntos abaixo. Observe que $M_2$ é um emparelhamento em $G[V_2]$, $A_2$ é uma cobertura de $G[V_2]$, e $|M_2|=|A_2|$.
Como todos os nós de $G$ estão em $V_1\cup V_2$, a união $M_1\cup M_2$ é um emparelhamento em $G$ e $A_1\cup A_2$ é uma cobertura de $G$. É claro que $|M_1\cup M_2|=|A_1\cup A_2|$. Portanto, o emparelhamento $M_1\cup M_2$ é máximo.
Exemplo 8.5: Seja $G$ o grafo bipartido representado pela matriz abaixo. (Use o gabarito de posição dos nós para fazer uma figura.) Submetemos $G$ ao algoritmo EmpBipartidoPerfeito. As primeiras três iterações encontram o emparelhamento $\conj{\textcolor{blood}{ab},\textcolor{blood}{cd}}$.
A quarta iteração constrói uma árvore alternante com raiz $e$. A árvore se revela frustrada e a execução do algoritmo termina na linha 10 com o seguinte resultado (compare com o exemplo 7.3 do capítulo 7):
Agora submeta o grafo $G-V_1$ ao algoritmo EmpBipartidoPerfeito. Esta segunda execução do algoritmo termina na linha 13 e devolve o emparelhamento perfeito $M_2:=\conj{ab,fg,hi}$. Observe que $A_2:=\conj{a,g,i}$ é uma cobertura de $G-V_1$ e $|A_2|=|M_2|$.
Se juntarmos os resultados das duas execuções de EmpBipartidoPerfeito, teremos o emparelhamento $M_1\cup M_2$ e a cobertura $A_1\cup A_2$ de $G$. O emparelhamento é máximo pois $|M_1 \cup M_2| = |A_1\cup A_2|$.
Podemos descrever agora um algoritmo para o
problema 8.A sem restrições.
Dado um grafo arbitrário $G=(V,E)$,
o algoritmo deve produzir um emparelhamento $M$ e
um subconjunto $A$ de $V$ tais que
\begin{equation}\label{eq:min-exposed-nodes}
|V|-2|M| \leq \oc(G{-}A)-|A|\text{.}
\end{equation}
De acordo com o lema 8.1,
um tal $M$ e máximo e \eqref{eq:min-exposed-nodes} vale com $=$
no lugar de $\leq$
.
O algoritmo será descrito em estilo recursivo. Comece por submeter $G$ ao algoritmo EmpPerfeito da seção 7.6. Se a execução do algoritmo termina na linha 17 e devolve um emparelhamento perfeito $M$, então o par $(M,\emptyset)$ satisfaz \eqref{eq:min-exposed-nodes}. Essa caso está na base da recursão.
Suponha agora que a execução do algoritmo termina na linha 13. Então temos um grafo derivado $G'$, um emparelhamento $M'$ em $G'$, e uma árvore $M'$-alternante frustrada $T'$ em $G'$. Temos também o conjunto $A'$ de nós brancos de $T'$ e o conjunto $B'$ de nós pretos de $T'$. Todos os nós de $A'$ são originais (veja a seção 7.5), enquanto $B'$ pode conter pseudonós. Como se sabe, $|B'| = |A'|+1$ e toda aresta de $G'$ com uma ponta em $B'$ tem a outra em $A'$. Ademais, $M'$ deixa exatamente um nó exposto no grafo induzido $G'[V(T')]$ e $\oc(G'{-}A') - |A'| \geq |B'|-|A'| =1$.
Seja $V_1$ o conjunto de nós do grafo original $G$ que correspondem aos nós de $T'$. (Em termos da notação usada na seção 7.5, $V_1$ é o união de todos os conjuntos $S(v)$ com $v$ em $V(T')$.) Seja $A_1$ um nome alternativo para $A'$ e observe que nenhuma aresta de $G$ liga $V_1\setm A_1$ a $V(G)\setm V_1$. Seja $M$ o resultado de Expande $(G',M')$. É claro que $M$ é um emparelhamento no grafo original $G$, mas esse emparelhamento pode não ser máximo pois EmpPerfeito pode não ter explorado o grafo todo. Seja $M_1$ o conjunto das arestas de $M$ que têm ambas as pontas em $V_1$. Observe que $M_1$ deixa exatamente um nó exposto no grafo induzido $G[V_1]$, ou seja, que $|V_1|-2|M_1|=1$. Observe também que $\oc(G[V_1]{-}A_1) - |A_1| \geq \text{}$ $\oc(G'{-}A') - |A'| \geq 1$.
Se $V_1=V(G)$ então estamos na base da recursão, pois o par $(M_1,A_1)$ satisfaz \eqref{eq:min-exposed-nodes}. Suponha agora que $V_1\neq V(G)$. Submeta o grafo $G-V_1$ ao algoritmo que estamos descrevendo. Isso produzirá um emparelhamento $M_2$ em $G-V_1$ e um subconjunto $A_2$ de $V(G-V_1)$ que satisfazem \eqref{eq:min-exposed-nodes} no papel de $(M,A)$. Então o par $(M_1\cup M_2,A_1\cup A_2)$ satisfaz \eqref{eq:min-exposed-nodes}, como desejamos.
Exemplo 8.6: Seja $G$ o grafo representado pela matriz de adjacências abaixo. (Use o gabarito de posição dos nós para fazer uma figura.) Usaremos o algoritmo EmpPerfeito para encontrar um emparelhamento máximo em $G$.
Submeta $G$ ao algoritmo EmpPerfeito. O algoritmo produz o emparelhamento $M:=\conj{bc,de,gh}$. O grafo derivado $G'$ tem um pseudonó $C:=\conj{c,d,e}$. A execução do algoritmo termina na linha 13 com $M':=\conj{bC}$ e com a árvore $M'$-alternante frustrada $T'$ que tem raiz $a$ e arestas $ab$ e $bC$. O conjunto de nós brancos é $A':=\conj{b}$ e o conjunto de nós pretos é $B':=\conj{a, C}$. A tabela abaixo mostra $V_1$, $M_1$ e $A_1$. Observe que $\oc(G[V_1]{-}A_1) - |A_1| = \text{}$ $1 = |V_1| - 2|M_1|$.
Agora submeta $G-V_1$ ao algoritmo EmpPerfeito. O algoritmo produz o emparelhamento $M:=\conj{gh}$. O grafo derivado $G'$ não tem pseudonós é portanto é igual a $G$. A execução do algoritmo termina na linha 13. A árvore $M$-alternante frustrada $T'$ tem raiz $f$ e arestas $fg$ e $gh$. O conjunto de nós brancos é $A':=\conj{g}$ e o conjunto de nós pretos é $B':=\conj{f,h}$. A tabela abaixo mostra $V_2$, $M_2$, e $A_2$. Observe que $\oc(G[V_2]{-}A_2) - |A_2| = \text{}$ $1 = |V_2| - 2|M_2|$.
Temos $V_1\cup V_2 = V(G)$. O emparelhamento $M_1\cup M_2$ e o conjunto de nós $A_1\cup A_2$ satisfazem \eqref{eq:min-exposed-nodes}.
O algoritmo que acabamos de esboçar é conhecido como algoritmo de Edmonds para emparelhamento máximo ou algoritmo das flores (= blossom algorithm). Esse algoritmo, acompanhado da competente análise de correção, constitui uma prova do teorema 8.2.
Veja uma demonstração do algoritmo no sítio The Blossom Algorithm for Maximum Matching do Wolfram Demonstrations Project.
Implementação. Com estruturas de dados apropriadas, é possível implementar o algoritmo de Edmonds para emparelhamento máximo de modo que ele consuma $\Oh(mn \log n)$ unidades de tempo, sendo $m$ o número de arestas e $n$ o número de nós do grafo. Dada a complexidade da lógica do algoritmo, é de surpreender que uma implementação tão eficiente seja possível.
É interessante examinar uma prova não algorítmica do teorema de Tutte–Berge. A prova depende dos conceitos de caminho alternante e caminho aumentador introduzidos na seção 6.3, bem como da operação de contração de circuitos definida na seção 7.5.
Se $C$ é um circuito de um grafo $G$, denotamos por $G{\times}C$ o grafo que resulta da contração de $C$. O seguinte lema mostra que a contração de um circuito de comprimento ímpar não aumenta a deficiência $\df()$ do grafo:
Lema 8.3 (da contração de circuito ímpar) Se $C$ é um circuito ímpar num grafo $G$ então $\df(G{\times}C)\geq \df(G)$.
Prova:
Como já observamos na
seção 7.5,
a contração de um circuito ímpar $C$ tem a seguinte propriedade:
qualquer emparelhamento $M'$ no grafo $G{\times}C$ pode ser
expandido
para dentro
de $C$ de modo a produzir um emparelhamento
$M\subseteq M'\cup E(C)$ em $G$
tal que $|V|-2|M| = |V'|-2|M'|$,
sendo $V:=V(G)$ e $V':=V(G{\times}C)$.
Suponha agora que $M'$ é um emparelhamento máximo em $G{\times}C$. Se $M$ é o emparelhamento obtido a partir de $M'$ como no parágrafo anterior então \[ \df(G) \leq |V| - 2|M| = |V'| - 2|M'| = \df(G{\times}C)\text{,} \] como queríamos mostrar. ■
Dizemos que um circuito ímpar $C$ é justo (= tight) se $\df(G{\times}C)=\df(G)$. É claro que $C$ é justo se e somente se $\nu(G{\times}C) = \nu(G) - \frac{1}{2} (|V(C)|-1)$ e portanto existe um emparelhamento máximo em $G$ que usa exatamente $\floor{\frac{1}{2} |V(C)|}$ arestas de $C$.
Se todos os circuitos ímpares fossem justos, o problema de encontrar um emparelhamento máximo em $G$ poderia ser reduzido ao problema de emparelhamento máximo no grafo $G{\times}C$. Infelizmente, nem todo circuito ímpar é justo.
Para lidar com circuitos ímpares que não são justos, precisamos do conceito de nó essencial. Um nó $v$ de um grafo $G$ é essencial (= essential) se $\nu(G-v) \lt \nu(G)$, ou seja, se todo emparelhamento máximo em $G$ satura $v$. É claro que $v$ é essencial se e somente se \[ \df(G-v) > \df(G)\text{.} \]
Exemplo 8.8: No grafo induzido por um circuito de comprimento par, todos os nós são essenciais. Já no grafo induzido por um circuito ímpar, nenhum nó é essencial.
Exemplo 8.9: Na árvore da figura, somente os nós $a$ e $b$ são essenciais.
Lema 8.4 Para qualquer grafo $G$ e qualquer subconjunto próprio $A$ de $V(G)$, se $\df(G) \leq \oc(G{-}A) - |A|$ então todo nó de $A$ é essencial.
Prova: Seja $v$ um nó de $A$ e adote a notação $A{-}v:=A\setm\conj{v}$. Conforme o lema 8.1 (com $G{-}v$ no papel de $G$ e $A{-}v$ no papel de $A$), temos $\df(G{-}v) \geq \oc((G{-}v) - (A{-}v)) - |A{-}v|$. Como $(G-v) - (A{-}v) = G{-}A$, temos \[ \begin{split} \df(G{-}v) & \geq \oc(G{-}A) - (|A| - 1)\\ & \geq \oc(G{-}A) - |A| + 1\\ & \geq \df(G) + 1 \end{split} \] e portanto $v$ é essencial. ■
Lema 8.5 (dos nós essenciais adjacentes) Para qualquer aresta $vw$ de um grafo $G$, se $v$ e $w$ não são essenciais então $vw$ pertence a algum circuito ímpar justo $C$; ademais, $C$ é um nó não-essencial de $G{\times}C$.
Prova: Seja $M_1$ um emparelhamento máximo que não satura $v$ e $M_2$ um emparelhamento máximo que não satura $w$. Note que $M_1$ satura $w$ e $M_2$ satura $v$. Considere o grafo $H$ induzido por $M_1\symdiff M_2$. A componente conexa de $H$ que contém $v$ consiste em um caminho simples $P$ com origem $v$. Se a última aresta de $P$ estivesse em $M_2$, teríamos um caminho $M_1$-aumentador, o que contradiz a maximalidade de $M_1$. Se a última aresta de $P$ estivesse em $M_1$ e o último nó de $P$ fosse diferente de $w$, então o caminho $(w,v)\cdot P$ seria $M_2$-aumentador, o que contradiz a maximalidade de $M_2$. Portanto, $P$ termina em $w$ e tem comprimento par. Logo, $C := P\cdot (w,v)$ é um circuito ímpar.
O emparelhamento máximo $M_1$ contém $\floor{|V(C)|/2}$ arestas de $C$. Logo $C$ é justo. Finalmente, $M_1\setm E(C)$ é um emparelhamento máximo em $G{\times}C$ e não satura o nó $C$ de $G{\times}C$. ■
Prova do teorema de Tutte–Berge. Agora que os lemas 8.3 (da contração de circuito ímpar), 8.4 e 8.5 (dos nós essenciais adjacentes) prepararam o terreno, podemos provar o teorema de Tutte–Berge.
Prova: Seja $G$ um grafo. O lema 8.1 já mostrou que $|V(G)|-2|M| \geq \oc(G{-}A)-|A|$ para qualquer emparelhamento $M$ e qualquer subconjunto próprio $A$ de $V(G)$. Em particular, $\df(G) \geq \text{}$ $\oc(G{-}A)-|A|$ para qualquer $A\subset V(G)$. Resta mostrar que existe $A\subset V(G)$ tal que \[ \df(G) \leq \oc(G{-}A)-|A|\text{.} \] A prova é uma indução no número de arestas de $G$. Se o conjunto de arestas é vazio, a afirmação vale com $A=\emptyset$. Agora suponha que o conjunto de arestas não é vazio e seja $vw$ uma aresta qualquer. Há dois casos a considerar.
Caso 1: uma das pontas de $vw$ é um nó essencial. Ajuste a notação (intercambinado $v$ e $w$ se necessário) de modo que $v$ seja o nó essencial e portanto $\df(G-v) > \text{}$ $\df(G)$. Seja $G':=G-v$. Por hipótese de indução, podemos supor que existe $A' \subset V(G')$ tal que $\df(G') \leq \text{}$ $\oc(G'-A')-|A'|$. Seja $A:= A'\cup\conj{v}$ e observe que $G-A = G'-A'$. Logo, \[ \begin{split} \df(G) & \leq \df(G{-}v) - 1\\ & = \df(G') - 1\\ & \leq \oc(G'-A') - |A'| - 1\\ & = \oc(G{-}A) - |A|\text{,} \end{split} \] como queríamos mostrar.
Caso 2: $v$ e $w$ não são essenciais. Pelo lema 8.5, $v$ e $w$ pertencem a um circuito ímpar justo, digamos $C$. Seja $G' := G{\times}C$. Por hipótese de indução, podemos supor que existe $A'\subset V(G')$ tal que $\df(G') \leq \text{}$ $\oc(G'-A')-|A'|$. Pelo lema 8.3, $\df(G') \geq \text{}$ $\df(G)$. Logo, \[ \df(G) \leq \oc(G'-A')-|A'|\text{.} \] Pelo lema 8.5, o nó $C$ de $G'$ não é essencial. Portanto, o lema 8.4 (com $G'$ no papel de $G$ e $A'$ no papel de $A$) garante que o nó $C$ não pertence a $A'$. Assim, $A'\subset V(G)$. Como $C$ é ímpar, toda componente ímpar de $G'-A'$ corresponde a uma componente ímpar de $G{-}A'$. Portanto, $\oc(G'-A') = \text{}$ $\oc(G{-}A')$ e assim \[ \df(G) \leq \oc(G{-}A') - |A'|\text{,} \] como queríamos mostrar. ■
Esta prova do teorema 8.2 não é algorítmica pois não temos um algoritmo para decidir se um dado nó é essencial. Assim, a prova não pode servir de base para um algoritmo recursivo que alcule um emparelhamento máximo.
A expressão $G[D]$ representa o subgrafo de $G$ induzido por $D$. [CCPS 5.6]
Existe um algoritmo polinomial para encontrar um emparelhamento máximo em qualquer grafo $G$. O algoritmo produz não só um emparelhamento máximo $M$ como também um prova da maximalidade de $M$ na forma de um subconjunto próprio $A$ de $V(G)$ tal que $|M| = \frac{1}{2} \big(|V| - \oc(G{-}A) + |A|\big)$.