Componentes biconexas e articulações de um grafo

Este capítulo trata de grafos não-dirigidos que são robustos no seguinte sentido: o grafo permanece conexo mesmo quando qualquer um de seus vértices é removido.

Articulações

Uma articulação (= articulation point) ou vértice de corte (= cut vertex) de um grafo não-dirigido é qualquer vértice que tenha grau pelo menos 2 e incida em duas arestas que não pertencem a um mesmo circuito.

Um vértice v é uma articulação se e somente se a remoção de v produz um grafo com mais componentes conexas que o grafo original. Essa observação permite decidir se um dado vértice é uma articulação. Esse algoritmo é consome tempo linear no tamanho do grafo.

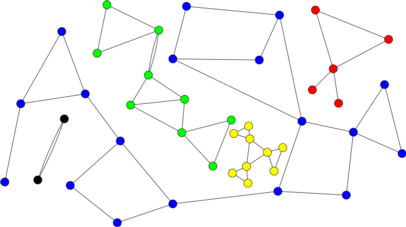
Exemplo A. Considere o grafo não-dirigido representado na figura. O vértice 12 não é uma articulação pois tem grau menor que 2. O vértice 2 não é uma articulação pois as duas únicas arestas que incidem em 2 pertencem a um mesmo circuito. O vértice 4 é uma articulação pois as arestas 4-3 e 4-9 não pertencem a um mesmo circuito (embora as arestas 4-3 e 4-5, por exemplo, pertençam a um mesmo circuito). O grafo tem uma só componente conexa, mas a remoção do vértice 4, por exemplo, produziria um grafo com duas componentes. O mesmo pode ser dito dos vértices 0, 5, 6, 7 e 11. Os demais vértices não são articulações.

O problema das articulações. Embora possamos decidir rapidamente se um dado vértice de um grafo não-dirigido é uma articulação, o seguinte problema é mais difícil:

Para resolver o problema, pode-se aplicar cegamente a definição de articulação (ou seja, verificar, para cada vértice, se sua remoção aumenta o número de componentes conexas do grafo). Mas é possível fazer algo bem mais eficiente.

É possível encontrar todas as articulações de um grafo não-dirigido de maneira muito rápida: basta usar uma variante apropriada da função UGRAPHbridges3(), que calcula as pontes de um grafo. Os detalhes ficam a cargo do leitor.

Exercícios 1

Considere o grafo não-dirigido definido pelo conjunto de arestas 0-1 1-2 2-0 1-3 1-4 4-5 5-6 6-4. Faça uma lista de todas as articulações do grafo.
Faça uma lista de todas as articulações do grafo não-dirigido definido pelo conjunto de arestas 8-9 3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
Seja v-w uma ponte em um grafo não-dirigido. Suponha que v tem outro vizinho além de w. Prove que v é uma articulação.
Quantas articulações tem uma árvore?
Quantas articulações um grafo não-dirigido com V vértices pode ter?
Articulações versus conexidade. Prove que um vértice é uma articulação se e somente se sua remoção aumenta o número de componentes conexas do grafo.
Reconhecimento de articulações. Escreva uma função que decida se um dado vértice de um grafo não-dirigido é uma articulação.
Algoritmo ingênuo. Implemente o seguinte algoritmo para o problema das articulações: para cada vértice do grafo, use a função UGRAPHconComps() para verificar se a remoção do vértice aumentaria o número de componentes conexas do grafo. (Sugestão: Não é necessário remover um vértice fisicamente. Marcar um vértice x com pre[x] ≠ -1 antes do início da busca tem o mesmo efeito que remover x virtualmente do grafo.) Quanto tempo esse algoritmo consome? Onde o algoritmo desperdiça tempo? Há alguma maneira óbvia de acelerar um pouco esse algoritmo?
Use uma variante da função UGRAPHconComps() para decidir se um grafo não-dirigido tem articulações. (Sugestão: Marcar um vértice x com pre[x] ≠ -1 antes do início da busca tem o mesmo efeito que remover x do grafo.) A função será lenta (consumo de tempo proporcional a V (V+E) num grafo com V vértices e E arestas).
??? [Sedgewick 18.36] Faça uma figura da árvore de busca em profundidade do grafo não-dirigido definido pelas arestas 3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4. (Adote a representação por listas de adjacência e insira as arestas, na ordem dada, num grafo inicialmente vazio.) Use a árvore para encontrar as articulações do grafo.
[Sedgewick 18.37] Repita o exercício anterior depois de representar o grafo por sua matriz de adjacências.
Algoritmo de articulações eficiente. Considere a função UGRAPHbridges3(), que calcula todas as pontes de um grafo não-dirigido. Modifique a função para que ela imprima uma lista de todas as articulações do grafo. (A raiz da floresta de busca deve receber cuidado especial: ela é uma articulação se e somente se tem dois ou mais filhos.)

Biligação entre vértices

Dois vértices s e t estão biligados se existem dois caminhos de s a t sem vértices internos em comum. A expressão sem vértices internos em comum significa que s e t são os dois únicos vértices comuns aos dois caminhos. Podemos dizer também que os dois caminhos são internamente disjuntos.

De acordo com essa definição, dois vértices adjacentes então estão biligados (pois se s e t são adjacentes então duas cópias do caminho s–t são internamente disjuntas). Da mesma forma, parece compatível com a definição dizer que todo vértice está biligado a si mesmo. Vamos procurar evitar esses dois casos extremos pois eles são um tanto estranhos e desconcertantes.

Vale lembrar que cada aresta consiste em dois arcos antiparalelos. Assim, o inverso de um caminho num grafo não-dirigido também é um caminho. Segue daí que dois vértices distintos e não-adjacentes estão biligados se e somente se pertencem a algum circuito simples.

Exemplo B. Considere o grafo não-dirigido representado na figura. Os vértices 0 e 2 estão biligados: os caminhos 0-6-2 e 0-1-2 ligam os dois vértices e são internamente disjuntos. Os vértices 5 e 11 não estão biligados (os caminhos 5-3-4-11 e 5-4-9-11 não são internamente disjuntos). Os vértices 0 e 8 também não estão biligados.

Exercícios 2

Transitividade. Mostre que a relação de biligação não é transitiva. (Isso é diferente do que acontece com a relação de ligação dupla.)
★ Biligação versus circuito. Mostre que dois vértices não adjacentes s e t de um grafo não-dirigido estão biligados se e somente se s e t pertencem a um mesmo circuito simples.
Algoritmo de biligação? Suponha dados vértices s e t de um grafo não-dirigido G. Considere o seguinte algoritmo: (1) encontre um caminho de s a t, (2) remova de G os vértices internos do caminho, (3) procure por um caminho de s a t no grafo resultante. Mostre que esse algoritmo não é capaz de decidir se s e t estão biligados.
Algoritmo de biligação. Esboce um algoritmo que receba um grafo não-dirigido e dois de seus vértices e decida se os vértices estão biligados.

Grafos biconexos

Um grafo não-dirigido é biconexo (= biconnected) ou 2-conexo se tem três ou mais vértices e cada dois vértices estão biligados (ou seja, pertencem a algum circuito simples). É claro que todo grafo biconexo é conexo.

(A restrição a grafos com 3 ou mais vértices é necessária. Sem ela, um grafo que tem apenas dois vértices e uma aresta seria considerado biconexo. Da mesma forma, um grafo com apenas um vértice também seria considerado biconexo. Esses casos extremos são desconcertantes e inconvenientes.)

Um grafo não-dirigido é biconexo se e somente se tem pelo menos 3 vértices, é conexo, e não tem articulações.

Um grafo não-dirigido é biconexo se e somente se permanece conexo depois da remoção de qualquer um de seus vértices. Assim, é preciso remover pelo menos 2 vértices de um grafo biconexo para que ele fique desconexo.

Exercícios 3

Mostre que todo grafo não-dirigido biconexo é conexo.
Prove que todo grafo não-dirigido biconexo é aresta-biconexo. A recíproca é verdadeira?
Suponha que todo vértice de um grafo não-dirigido pertence a um circuito. É verdade que o grafo é biconexo?
[Sedgewick 18.44] Quantas arestas no mínimo tem um grafo não-dirigido biconexo com V vértices?
Prove que um grafo não-dirigido biconexo permanece conexo depois da remoção de qualquer um de seus vértices. Prove a recíproca: se um grafo conexo G com 3 ou mais vértices permanece conexo depois da remoção de qualquer um de seus vértices então G é biconexo.
[Sedgewick 18.39] Seja G um grafo não-dirigido biconexo. Sejam s e t dois vértices de G. Prove que existem dois caminhos de s e t sem vértices internos em comum. (Sugestão: Tome um caminho de s a t. Os vértices internos desse caminho não são articulações. Use esse fato para construir dois caminhos de s a t sem vértices internos em comum.)

Componentes biconexas

Uma componente biconexa (= bloco??) de um grafo não-dirigido é um subgrafo ..........