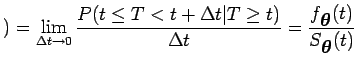Análise de Sobrevivência

Alexandre Galvão Patriota ¹

--------------------------------------------------

Atenção: O material apresentado neste site serve apenas de apoio para o estudo da disciplina de Análise de sobrevivência no Instituto de matemática e Estatística ministrada pelo professor Antônio Carlos Pedroso de Lima. Lembramos também que o curso é bem mais extenso e detalhado do que é apresentado aqui. O autor deste material é doutorando do Instituto de Matemática e Estatística da USP.

--------------------------------------------------

Análisar o tempo de vida é um assunto extremamente interessante para pesquisadores das áreas de biologia, medicina, engenharia, estatística entre outras. Estudos sobre o tempo de vida de pacientes com doenças incuráveis é um dos inúmeros exemplos na área médica, estudos sobre o tempo de duração de algum componente eletrônico é um exemplo na área de engenharia.

A característica principal desse tipo de dado é a presença de censuras nas observações e isto acarreta em algumas complicações de ordem técnica. Existem duas abordagens estatísticas para estimar a curva de sobrevivência, uma delas considera modelos paramétricos e outra modelos não paramétricos. A escolha de uma das abordagens não significa a exclusão da outra, por exemplo, o modelo não paramétrico pode indicar evidências de que um modelo paramétrico não está adequado. Por isso o uso das duas abordagens é essencial para garantir resultados fidedignos.

Na prática observamos os vetores $(T_1,\delta_i), \ldots , (T_n,\delta_n)$, sendo $T_i$ tempo observado para a $i$-ésima unidade experimental (u.e.), sendo que esta u.e. pode ter sido uma falha ou uma censura, ou seja, poderemos definir $T_i^{0}$ o tempo de sobrevivência da $i$-ésima u.e. e $C_i$ o tempo até a censura da $i$-ésima u.e., então

$$T_i = min \{T_i^{0},C_i\},$$

e $\delta_i$ é o indicador de falha, é 1 se a $i$-ésima u.e. falhou e 0 caso contrário

$$\delta_i = I(T_i^{0}\leq C_i)$$

Algumas suposições sobre $T_i^{0}$ e $C_i$ são feitas

• $T_i^{0}$ tem função densidade de probabilidade (f.d.p.) e função de sobrevivência, dadas por $f_{\mbox{\boldmath {$\theta$}}}(t_i^{0})$ e $S_{\mbox{\boldmath {$\theta$}}}(t_i^{0})$;

• $C_i$ tem f.d.p. e função de sobrevivência, dadas por $g_{\mbox{\boldmath {$\gamma$}}}(c_i)$ e $G_{\mbox{\boldmath {$\gamma$}}}(c_i)$;

• $T_i^{0}$ e $C_i$ são independentes;

• $\theta$ e $\gamma$ não compartilham parâmetros, ou seja, as censuras não são informativas.

Com as suposições acima, é fácil mostrar que a verossimilhança para $\theta$ é

$$L( \mbox{\boldmath {$\theta$}} ) = \prod_{i=1}^{n} f_{\mbox{\boldmath {$\theta$}}}(t_i)^{\delta_i} S_{\mbox{\boldmath {$\theta$}}}(t_i)^{1-\delta_i}$$ (1)

A função Taxa de falhas é definida abaixo

$$\alpha(t,$$$\theta$$$) = \lim_{\Delta t \rightarrow 0} \dfrac{P(t \leq T < t+\Delta t ... ... \dfrac{f_{\mbox{\boldmath {$\theta$}}}(t)}{S_{\mbox{\boldmath {$\theta$}}}(t)}$$