Modelos de vida acelerada

Na prática algumas dificuldades são impostas pela resistência dos materiais que queremos observar as falhas, por exemplo, se estivermos interessandos em analisar o tempo que uma determinada lâmpada leva para queimar, seria viável aumentar a tensão para que o tempo de espera não seja tão longo. Chamaremos a variável que está sob condições normais de $T_0$ e o modelo que está sob a tensão $x > 0$ de $T_x$, consideraremos que quando $x = 0$ a variável está sob as condições normais. Assim, a classe dos modelos de vida acelerada é definida abaixo.

Se a distribuição do tempo de sobrevivência da variável sob a tensão $x$, $T_x$ tem a mesma distribuição que $T_0 \exp(\beta x)$, ou seja,

$$T_x \stackrel{D}{=}T_0\exp(\beta x)$$

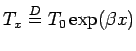
Verifica-se que os modelos exponencial e weibull pertencem a essa classe. Para o modelo exponencial teremos

$$f_{T_0}(t) = \lambda \exp( - \lambda t)$$ e $$f_{T_x}(t) = \lambda\exp(-\beta x) \exp( - \lambda t \exp(-\beta x))$$

fazendo $\alpha = \log(\lambda)$ teremos

$$f_{T_x}(t) = \exp(\alpha-\beta x ) \exp( - t \exp(\alpha -\beta x))$$

Nos modelos de vida acelerada observamos as variáveis $(T_{x_1},x_1), \ldots,(T_{x_n},x_n)$ e a densidade para $T_{x_i}$, para o caso exponencial é dada por

$$f_{T_{x_i}}(t) = \exp($$$X$$$_i$$$\beta$$$) \exp( - t \exp($$$X$$$_i$$$\beta$$$))$$

sendo $X$$_i = (1 , x_i)$ e $\beta$$= (\alpha, \beta)$. O estimador para $\beta$ é obtido via máxima verossimilhança já visto na seção . Assim, para voltarmos ao modelo sem tensão, basta fazer $x = 0$.