Modelos Paramétricos

Assim para os modelos paramétricos temos na tabela

a f.d.p e função de sobrevivência para algumas distribuições.

**Tabela:** Densidade e função de sobrevivência para distribuições
$\begin{table} \begin{center} $ \begin{array}{lcccc}\hline \mbox{Distribuição} & ... ...mbda}{\rho}\right) &(\lambda,\rho)\\ \hline \end{array}$ \end{center}\end{table}$

Nos modelos paramétricos a função de sobrevivência e taxa de falhas dependem de um vetor de parâmetros $\theta$ que pode ser estimado via máxima verossimilhança, desta forma os estimadores de máxima verossimilhança para $\theta$ são obtidos maximizando o log da verossimilhança dado abaixo

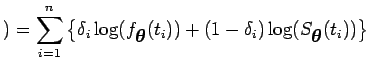
$\displaystyle \ell($ $\theta$ $\displaystyle ) = \sum_{i=1}^{n} \left\{\delta_i \log(f_{\mbox{\boldmath {$\theta$}}}(t_i)) + (1-\delta_i)\log(S_{\mbox{\boldmath {$\theta$}}}(t_i))\right\}$

$\displaystyle \mbox{\boldmath {$U$}}$ $\displaystyle ($ $\displaystyle \mbox{\boldmath {$\theta$}}$ $\displaystyle ) = \dfrac{\partial \ell(\mbox{\boldmath {$\theta$}})}{\partial \... ...a(t_i,\mbox{\boldmath {$\theta$}})f'_{\mbox{\boldmath {$\theta$}}}(t_i)\right\}$

(2)

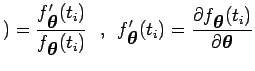
$\displaystyle v(t_i,$ $\theta$ $\displaystyle ) = \dfrac{f'_{\mbox{\boldmath {$\theta$}}}(t_i)}{f_{\mbox{\boldm... ...ial f_{\mbox{\boldmath {$\theta$}}}(t_i)}{\partial \mbox{\boldmath {$\theta$}}}$

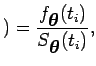
$\displaystyle \alpha(t_i,$ $\theta$ $\displaystyle )=\dfrac{f_{\mbox{\boldmath {$\theta$}}}(t_i)}{S_{\mbox{\boldmath {$\theta$}}}(t_i)},$

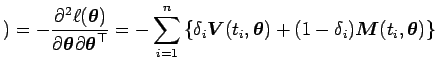
$\Sigma$ $\displaystyle ($ $\theta$ $\displaystyle ) = -\dfrac{\partial^2 \ell(\mbox{\boldmath {$\theta$}})}{\partia... ... + (1 -\delta_i)\mbox{\boldmath {$M$}}(t_i,\mbox{\boldmath {$\theta$}})\right\}$

$\displaystyle (t_i,$ $\theta$ $\displaystyle )= \dfrac{\partial v(t_i,\mbox{\boldmath {$\theta$}})}{\partial \... ...mbox{\boldmath {$\theta$}}}(t_i)\right]}{\partial \mbox{\boldmath {$\theta$}}}$

Desta forma os estimadores de máxima verossimilhança são obtidos usando o algoritmo de Newton Raphson

$\displaystyle \hat{\mbox{\boldmath {$\theta$}}}_{k+1} = \hat{\mbox{\boldmath {$... ...heta$}}}_{k})^{-1}\mbox{\boldmath {$U$}}(\hat{\mbox{\boldmath {$\theta$}}}_{k})$

Definimos diag como sendo uma matrix de zeros fora da diagonal principal e com os elementos de na diagonal principal. Assim, a convergência é obtida quando $\epsilon_{k} = \max\left\{ \mbox{diag}(\mbox{\boldmath {$\theta$}}_{k-1})^{-1}... ...mbox{\boldmath {$\theta$}}_k - \mbox{\boldmath {$\theta$}}_{k-1}\right)\right\}$ é suficientemente pequeno. A estimação da função de sobrevivência e da função taxa de falhas é feita utilizando as propriedades de invariância dos estimadores de máxima verossimilhança, desta forma são dadas por

$\displaystyle \hat{S}_{\mbox{\boldmath {$\theta$}}}(t) = S_{\hat{\mbox{\boldmat... ...}(t,\mbox{\boldmath {$\theta$}}) = \alpha(t,\hat{\mbox{\boldmath {$\theta$}}}).$

Os testes de hipóteses do tipo $\theta$ contra $\theta$ $\neq$ podem ser feitos via estatística de wald

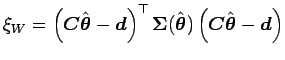
$\displaystyle \xi_W = \left(\mbox{\boldmath {$C$}}\hat{\mbox{\boldmath {$\theta... ...ldmath {$C$}}\hat{\mbox{\boldmath {$\theta$}}} - \mbox{\boldmath {$d$}}\right)$

A distribuição assintótica de $\xi_W$ é uma $\chi^2(c)$ , sendo o posto da matrix .

A análise de resíduos pode ser feita utilizando o resíduo de Cox-Snell definido por

$\displaystyle r_i = - \log(S_{\hat{\mbox{\boldmath {$\theta$}}}}(t_i))$

Se o modelo for adequado então $r_i \sim EXP(1)$ . Assim poderíamos fazer gráficos quantil quantil dos resíduos de Cox-Snell contra uma distribuição , caso os pontos do gráfico estejam próximos de uma reta com inclinação de aproximadamente 45 graus aceitamos o modelo proposto.