Modelos de regressão

É comum existir heterogeneidade da população em estudo e é razoável separar a população em subpopulações mais homogeneas ou inserir uma covariável para diminuir a variabilidade.

O modelo exponencial é o mais simples, e será visto com mais detalhes. Lembramos que a densidade e a função sobrevivência da distribuição exponencial são

$\displaystyle f_{T_i}(t_i) = \lambda \exp(-\lambda t_i)$ e $\displaystyle S_{\lambda}(t_i) = \exp(-\lambda t_i)$

Suponha que os vetores $_1,\delta_1), \ldots , (T_n,$ $_n,\delta_n)$ são observados, a função taxa de falhas de um modelo exponencial é $\alpha($ $\theta$ $,t_i) = \lambda$ , neste caso $\theta$ $= \lambda$ , verifica-se que a função taxa de falhas não depende do tempo. A inclusão das covariáveis no modelo exponencial é feita através da função taxa de falhas da seguinte forma

$\displaystyle \alpha(\lambda,t_i) = \lambda = \exp($ $\displaystyle ^{\top}_i$ $\beta$ $\displaystyle )$

sendo $_i^{\top} = (x_{1i}, \ldots, x_{pi})$ e $\beta$ $= (\beta_1,\ldots ,\beta_p)^{\top}$ . O log da verossimilhança é dado por

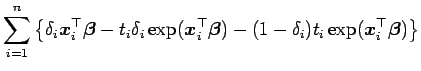$\displaystyle \ell($ $\displaystyle \mbox{\boldmath {$\beta$}}$ $\displaystyle )$	$\displaystyle =$	$\displaystyle \sum_{i=1}^{n} \left\{\delta_i \mbox{\boldmath {$x$}}_i^{\top}\mb... ...ta_i)t_i\exp(\mbox{\boldmath {$x$}}_i^{\top}\mbox{\boldmath {$\beta$}})\right\}$
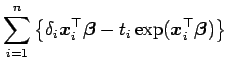	$\displaystyle =$	$\displaystyle \sum_{i=1}^{n} \left\{\delta_i \mbox{\boldmath {$x$}}_i^{\top}\mb... ...}} - t_i\exp(\mbox{\boldmath {$x$}}_i^{\top}\mbox{\boldmath {$\beta$}})\right\}$

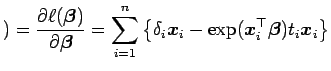
$\displaystyle ($ $\beta$ $\displaystyle ) = \dfrac{\partial \ell(\mbox{\boldmath {$\beta$}})}{\partial \m... ... {$x$}}_i^{\top}\mbox{\boldmath {$\beta$}})t_i\mbox{\boldmath {$x$}}_i\right\}$

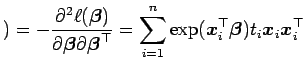
$\displaystyle ($ $\beta$ $\displaystyle ) = - \dfrac{\partial^2 \ell(\mbox{\boldmath {$\beta$}})}{\partia... ...boldmath {$\beta$}})t_i\mbox{\boldmath {$x$}}_i\mbox{\boldmath {$x$}}_i^{\top}$

Os estimadores de máxima verossimilhança para $\beta$ são obtidos iterativamente usando o algoritmo de Newton Raphson abaixo

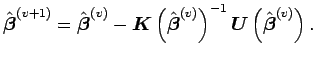
$\displaystyle \hat{\mbox{\boldmath {$\beta$}}}^{(v+1)} = \hat{\mbox{\boldmath {... ...{-1}\mbox{\boldmath {$U$}}\left(\hat{\mbox{\boldmath {$\beta$}}}^{(v)}\right).$

Poderemos usar as estatísticas de Wald, razão de verossimilhanças e escore para testar a hipótese de $\beta$ contra $\beta$ $\neq$ . Uma outra forma de estimar $\beta$ é tranformando a variável observada fazendo $Y_i = \log(T_i)$ , teremos que a densidade e função de sobrevivência de $W_i = Y_i - \log(\lambda)$ são dadas por

$\displaystyle f_W(w) = \exp(w - \exp(w))$ e $\displaystyle S_W(w) = \exp(-\exp(w))$

$\displaystyle Y_i =$ $\displaystyle _i^{\top}$ $\beta$ $\displaystyle + w_i$

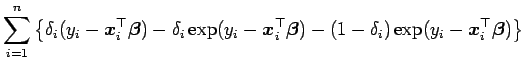$\displaystyle \ell($ $\displaystyle \mbox{\boldmath {$\beta$}}$ $\displaystyle )$	$\displaystyle =$	$\displaystyle \sum_{i=1}^{n} \left\{\delta_i(y_i- \mbox{\boldmath {$x$}}_i^{\to... ...i)\exp(y_i - \mbox{\boldmath {$x$}}_i^{\top}\mbox{\boldmath {$\beta$}})\right\}$
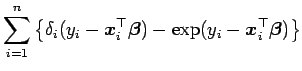	$\displaystyle =$	$\displaystyle \sum_{i=1}^{n} \left\{\delta_i (y_i -\mbox{\boldmath {$x$}}_i^{\t... ... \exp( y_i - \mbox{\boldmath {$x$}}_i^{\top}\mbox{\boldmath {$\beta$}})\right\}$

nota-se que se derivarmos o log da verossimilhança acima teremos os mesmos estimadores para $\beta$ quando não fazemos transformação alguma. Quando o tempo de falhas tem distribuição log-normal a aplicação do logarítmo no tempo observado facilita as contas, pois o modelo se reduz ao modelo linear clássico normal com observações censuradas, no caso de falhas com distribuição gamma, weibull e valor extremo a aplicação do logarítimo também facilita a obtenção do estimador de $\beta$ .