Next: Modelo de Cox Up: Análise de Sobrevivência Previous: Modelos de vida acelerada
O objetivo em análise de sobrevivência é estimar a função de sobrevida da variável em estudo. Uma metodologia interessante para tratar esse problema é a estimação não paramétrica, pois neste caso não impomos um modelo teórico para as falhas e/ou censuras observadas. A função de sobrevivência possui algumas propriedades, tais como, continuidade à esquerda, ![]() e
e
![]() . A figura abaixo nos mostra a curva de sobrevivência de uma variável aleatória com distribuição exponencial.
. A figura abaixo nos mostra a curva de sobrevivência de uma variável aleatória com distribuição exponencial.
Em (a) é apresentado a curva teórica, em (b) dividimos o tempo em partições iguais com amplitude de 0,5, em (c) dividimos em amplitudes de 0,1. Percebemos que se a amplitude tender a zero teremos a verdadeira curva de sobrevivência. Então poderemos definir a partição
![]() um estimador para a curva de sobrevida seria uma função escada dada por
um estimador para a curva de sobrevida seria uma função escada dada por
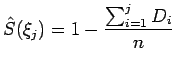
sendo ![]() as observações que falharam no intervalo
as observações que falharam no intervalo
![]() . No caso em que não temos censuras este seria o estimador da função de sobrevida, porém em análise de sobrevivência é necessário considerar as censuras no processo de estimação da curva de sobrevivência. Para isso definiremos algumas quantidades.
. No caso em que não temos censuras este seria o estimador da função de sobrevida, porém em análise de sobrevivência é necessário considerar as censuras no processo de estimação da curva de sobrevivência. Para isso definiremos algumas quantidades.
A função de sobrevivência pode ser escrita como
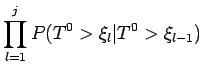 |
|||
![$\displaystyle \prod_{l=1}^{j} \left[1 - P(T^0 \leq \xi_l \vert T^0 > \xi_{l-1})\right]$](img122.png) |
|||
![$\displaystyle \prod_{l=1}^{j} [1 - q_l]$](img123.png) |
Para o caso em que não existem censuras ![]() pode ser estimado por
pode ser estimado por
![]() , ou seja o número de falhas dividido pelo número de unidades em risco em
, ou seja o número de falhas dividido pelo número de unidades em risco em ![]() . Neste mesmo caso verifica-se que
. Neste mesmo caso verifica-se que
![]() , então teremos
, então teremos
![$\displaystyle \prod_{l=1}^{j} [1 - \hat{q}_l]$](img129.png) |
|||
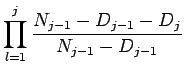 |
|||
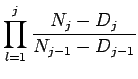 |
|||
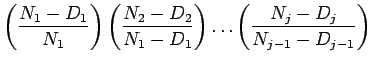 |
|||
como já visto anteriormente, pois
![]() . Para o caso de censuras, precisamos corrigir o denominador do estimador de
. Para o caso de censuras, precisamos corrigir o denominador do estimador de ![]() , pois o número de u.e. em risco está sendo sobre estimado. Se assumirmos que as unidades foram censuradas uniformemente ao longo do intervalo
, pois o número de u.e. em risco está sendo sobre estimado. Se assumirmos que as unidades foram censuradas uniformemente ao longo do intervalo ![]() , um estimador razoável para
, um estimador razoável para ![]() seria
seria
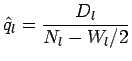 assim,
assim, ![$\displaystyle \widehat{S}(t) = \sum_{l:\xi_l < t}[1 - \hat{q}_l]$](img136.png)
também conhecido como estimador tábua de vida. E sua variância é dada por (ver Lawless 1982)
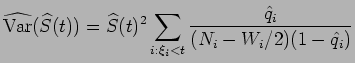
O estimador produto-limite, também conhecido como estimador Kaplan-Meier é obtido quando a partição
![]() é tal que a primeira falha ocorre em
é tal que a primeira falha ocorre em ![]() a segunda falha ocorre em
a segunda falha ocorre em
![]() , ... e a
, ... e a ![]() ésima falha ocorre em
ésima falha ocorre em
![]() , assim o estimador é dado por
, assim o estimador é dado por
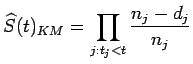
sendo ![]() o número de u.e. em risco em
o número de u.e. em risco em ![]() e
e ![]() o número de u.e. que falharam em
o número de u.e. que falharam em ![]() . Neste caso, estamos observando as falhas pontualmente, ou seja, no instante que ocorreu. No estimador tábua de vida, observamos as falhas em intervalos, sendo difícil conhecer o exato instante de cada falha. A variância para o estimador Kaplan-Meier da função de sobrevivência é dado por
. Neste caso, estamos observando as falhas pontualmente, ou seja, no instante que ocorreu. No estimador tábua de vida, observamos as falhas em intervalos, sendo difícil conhecer o exato instante de cada falha. A variância para o estimador Kaplan-Meier da função de sobrevivência é dado por
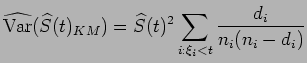
Na seção ![]() mostramos algumas propriedades de martingais e uma justificativa mais formal de que
mostramos algumas propriedades de martingais e uma justificativa mais formal de que
![]() para
para ![]() fixo.
fixo.
Outro estimador conhecido para ![]() é o estimador de Breslow, que utiliza o estimador de Nelson-Aalen. Definiremos algumas quantidades antes de apresentar os estimadores de Nelson-Aalen e Breslow. Definimos
é o estimador de Breslow, que utiliza o estimador de Nelson-Aalen. Definiremos algumas quantidades antes de apresentar os estimadores de Nelson-Aalen e Breslow. Definimos
![]() , sendo
, sendo
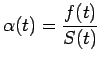 a função taxa de falhas. Assim
a função taxa de falhas. Assim
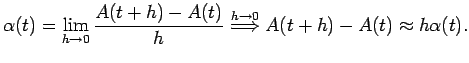
Desta forma
![]() ocorrer falha em
ocorrer falha em![]() está em risco
está em risco![]() e no instante de falha
e no instante de falha ![]() essa quantidade pode ser estimada por
essa quantidade pode ser estimada por ![]() . O estimador de Nelson-Aalen para
. O estimador de Nelson-Aalen para ![]() é dado por
é dado por
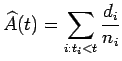
O estimador de Breslow para a função de sobrevivência é
Fleming-Harrington fizeram um estudo teórico do estimador de Breslow. Usando a aproximação
![]() quando
quando ![]() é pequeno, verificamos que o estimador de Breslow é assintoticamente equivalente ao estimador Kaplan-Meier.
é pequeno, verificamos que o estimador de Breslow é assintoticamente equivalente ao estimador Kaplan-Meier.
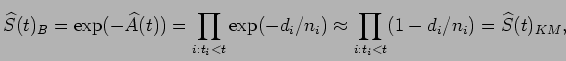
verifica-se que
![]() pois estamos supondo que
pois estamos supondo que
![]() .
.
A estimação não paramétrica de ![]() é muito útil mesmo quando queremos ajustar um modelo paramétrico, uma das forma de verificar se um modelo é adequado é fazer um gráfico de
é muito útil mesmo quando queremos ajustar um modelo paramétrico, uma das forma de verificar se um modelo é adequado é fazer um gráfico de
![]() versus
versus ![]() . Assim, se o modelo exponencial for adequado esse gráfico deverá ser próximo da relação
. Assim, se o modelo exponencial for adequado esse gráfico deverá ser próximo da relação
![]()
patriota 2006-04-29