Esta página descreve o algoritmo de busca em profundidade
(= depth-first search = DFS).
O algoritmo visita todos os vértices
de um digrafo numa determinada ordem,
que chamaremos pré-ordem
ou ordem DFS
.
Essa ordem dos vértices ajuda entender a estrutura do digrafo
e é muito útil, por exemplo,
para encontrar os ciclos e as componentes fortes do digrafo.
Esta página é inspirada na seção 3 do capítulo 22 do CLRS.
O algoritmo de busca em profundidade varre
(= scans)
um digrafo e visita todos seus vértices e todos seus arcos.
À medida que varre o digrafo,
o algoritmo pinta cada vértice de cinza e depois de preto.
Quando descobre um novo vértice,
o algoritmo pinta o vértice de cinza;
quando termina de visitar todos os vizinhos do vértice,
o algoritmo pinta o vértice de preto.
Os vértices cinza são considerados ativos
e os pretos
são considerados mortos
.
É mais simples escrever o
código do algoritmo em estilo recursivo.
Como não é possível varrer o digrafo todo de uma só vez,
a camada externa
do algoritmo é um driver
que invoca várias vezes
o algoritmo recursivo propriamente dito.
Cada invocação é uma etapa da busca.
O algoritmo recebe um digrafo G representado por um vetor Adj de listas de adjacência.
| Busca-em-Profundidade (G) |
| 1 . para cada r em V(G) |
| 2 .ooo cor[r] := branco |
| 3 . para cada r em V(G) |
| 4 .ooo se cor[r] = branco |
| 5 .oooooo DFS-r (G, r) ▷ nova etapa |
A rotina recursiva DFS-r
(o sufixo r
é a inicial de recursivo
)
tem acesso a um vetor cor que atribui
um rótulo branco, cinza ou preto a cada vértice do digrafo.
A rotina recebe um vértice branco r e
determina o conjunto, digamos X, de todos os vértices que pertencem a caminhos que começam em v e só usam vértices brancos.
Antes de parar, a rotina altera o vetor cor de modo que todos os vértices em X fiquem pretos.
| DFS-r (G, v) |
| 16 . cor[v] := cinza |
| 17 . para cada w em Adj[v] faça |
| 18 .ooo se cor[w] = branco ▷ w descoberto |
| 19 .oooooo então DFS-r (G, w) |
| 10 . cor[v] := preto ▷ v morre |
(Os vetores Adj e cor são tratados como variáveis globais.)
Na linha 9, a rotina DFS-r
é aplicada ao digrafo original G.
Isso pode criar a impressão de que a instância do problema que a rotina deve resolver
na linha 9 tem o mesmo tamanho da instância original.
Com isso, pode parecer que a
recursão nunca termina
(isto é, que a rotina entra em loop
).
Ocorre que o tamanho de uma instância não é medido pelo tamanho do digrafo
mas pelo número de vértices brancos.
Como um vértice cinza ou preto jamais fica branco,
o tamanho de uma instância nunca aumenta.
Além disso, v é branco quando DFS-r (G,&8201;v)
é invocada e logo fica cinza.
Assim, o tamanho da nova instância na linha 9
é menor que o tamanho da instância original.
Isso garante que a recursão é finita.
Ao final da execução do algoritmo Busca-em-Profundidade, todos os vértices do digrafo estarão pretos.
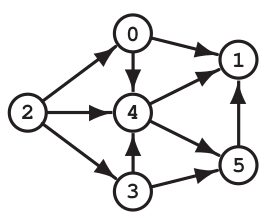
Exemplo A. Seja G o digrafo com vértices 0, 1, … , 5 definido pelas seguintes listas de adjacência:
0: (1, 4) 1: 2: (0, 3, 4) 3: (4, 5) 4: (1, 5) 5: (1)
Acompanhe o rastreamento da execução da algoritmo Busca-em-Profundidade sobre G. Uma linha típica do rastreamento mostra que o algoritmo percorreu um arco vw e invocou a encarnação DFS-r(w) de DFS-r.
0 DFS-r(0) 01 DFS-r(1) 01 04 DFS-r(4) 041 045 DFS-r(5) 0451 045 04 0 2 DFS-r(2) 20 23 DFS-r(3) 034 035 03 24 2
| 0 | 1 | 2 | 3 | 4 | 5 |
| ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ |
| C | C | ⋅ | ⋅ | ⋅ | ⋅ |
| C | P | ⋅ | ⋅ | ⋅ | ⋅ |
| C | P | ⋅ | ⋅ | C | ⋅ |
| C | P | ⋅ | ⋅ | C | C |
| C | P | ⋅ | ⋅ | C | P |
| C | P | ⋅ | ⋅ | P | P |
| P | P | ⋅ | ⋅ | P | P |
| P | P | C | ⋅ | P | P |
| P | P | C | C | P | P |
| P | P | C | P | P | P |
| P | P | P | P | P | P |
Um vértice v sozinho numa linha do rastreamento representa o fim do processamento de v, ou seja, o fim da execução da encarnação DFS-r (v) de DFS-r.
A tabela à direita mostra a evolução do vetor cor, com ⋅ , C e P significando branco, cinza e preto respectivamente.
Qual o consumo de tempo de Busca-em-Profundidade? É fácil constatar que o consumo de tempo de todas as execuções de todas as linhas exceto a linha 5 é Ο(n), sendo n o número de vértices de G. Agora considere a linha 5, que invoca a rotina DFS-r. O consumo de tempo dessa rotina, como o de qualquer algoritmo recursivo, pode ser descrito por uma recorrência. Infelizmente, a recorrência é um tanto complexa. Vamos estimar então, de uma só vez e de maneira um tanto informal, o tempo total de todas as execuções de DFS-r.
Para cada vértice v, a rotina DFS-r é invocada apenas uma vez com argumento v. (De fato, v é branco antes da chamada e torna-se cinza logo em seguida.) A execução da rotina com argumento v examina, diretamente, todos os arcos que saem de v e apenas esses. (O exame dos outros arcos acontece nas invocações de DFS-r na linha 9.) Portanto, na união de todas as execuções de DFS-r, cada arco do digrafo é examinado uma única uma vez. Como o exame de cada arco consome uma quantidade de tempo que não depende do tamanho do digrafo, o tempo total gasto nas execuções de DFS-r é Ο(m), sendo m o número de arcos do digrafo.
Concluímos assim que o algoritmo Busca-em-Profundidade consome
unidades de tempo. Como n + m é o tamanho do digrafo, o algoritmo é linear.
Cada vez que um novo vértice w é descoberto durante a busca DFS, é útil anotar o vértice v a partir do qual w foi descoberto. Para isso, basta usar um vetor de vértices, digamos pai, indexado pelos vértices e fazer pai[w] := v. Diremos que pai é um vetor de pais (= parent array = array of predecessors) da busca.
| Busca-em-Profundidade (G) |
| 1 . para cada v em V(G) |
| 2 .ooo cor[v] := branco |
| 3 . para cada r em V(G) |
| 4 .ooo se cor[r] = branco |
| 5 .oooooo pai[r] := r |
| 6 .oooooo DFS-r (G, r) |
| 7 . devolva pai |
Eis a versão apropriada de DFS-r:
| DFS-r (G, v) |
| 18 . cor[v] := cinza |
| 19 . para cada w em Adj[v] |
| 10 .ooo se cor[w] = branco |
| 11 .oooooo pai[w] := v |
| 12 .oooooo DFS-r (G, w) |
| 13 . cor[v] := preto |
O subdigrafo de G formado por todos os arcos vw tais que v = pai[w] é uma floresta radicada. Diremos que essa é a floresta DFS da busca. Os vértices r nas várias execuções da linha 5 (onde começa cada nova etapa da busca) são as raízes da floresta. A floresta DFS é um subdigrafo gerador do digrafo G.
Exemplo B. Considere novamente o digrafo do exemplo A. O algoritmo Busca-em-Profundidade produz uma floresta DFS que consiste em duas árvores: uma tem raiz 0 e a outra tem raiz 2. Veja o vetor de pais da floresta:
| v] | 0 | 1 | 4 | 5 | 2 | 3 |
| pai[v] | 0 | 0 | 0 | 4 | 2 | 2 |
Nesta tabela, os vértices estão listados na ordem em que foram descobertos. A tabela pode ser reescrita colocando a primeira linha em ordem crescente:
| v] | 0 | 1 | 2 | 3 | 4 | 5 |
| pai[v] | 0 | 0 | 2 | 2 | 0 | 4 |
0 2
/ \ |
1 4 3
\
5
Às vezes é útil redesenhar a floresta DFS de modo que a ordem dos vértices de cima para baixo e da esquerda para a direita correspondam à ordem em que os vértices foram examinados nas linhas 3 e 9 de DFS-r. Feito isso, os demais arcos do digrafo podem ser acrescentados à figura.
Arcos de avanço, de retorno, e cruzados. Suponha que F é uma floresta DFS de um digrafo G. Em relação a F, cada arco vw de G é de um dos seguintes tipos:
Essa classificação dos arcos é importante para entender o digrafo. Ela é usada por muitos algoritmos para diversos problemas.
Exemplo C. Aplique o algoritmo Busca-em-Profundidade ao digrafo da figura. Se começar pelo vértice 2, o algoritmo poduzirá a floresta DFS indicada na figura. Em relação a essa floresta, o arco 7 3 é de avanço. Os arcos 0 2, 4 5, 4 7, 5 7 e 6 2 são de retorno. Os arcos 0 4 e 6 4 são cruzados.
| v] | a | b | c | d | e | f | g |
| p[v] | c | c | c | d | a | d | a |
se cor[x] = branconas linhas 4 e 10 por
se pai[x] = nil. Implemente essas alterações.
No início desta página
referimo-nos vagamente à permutação em pré-ordem
dos vértices do digrafo.
Esta seção define o conceito de maneira mais precisa.
A permutação dos vértices em pré-ordem (= pre-order) é definida pela ordem em que os vértices ficam cinzentos durante uma busca em profundidade. A permutação em pós-ordem (= post-order) é definida pela ordem em que os vértices ficam pretos. É claro que essas permutações dependem da ordem em que os vértices são examinados na linha 3 de Busca-em-Profundidade e na linha 7 de DFS-r.
O seguinte algoritmo faz uma busca em profundidade num digrafo
e atribui dois números (= timestamps
a cada vértice w:
o número pré[w] é o momento em que o vértice fica cinza
(ou seja, o momento em que é descoberto)
e o número pós[w] é o momento em que o vértice fica preto
(ou seja, o momento em que morre
).
O algoritmo usa uma variável t como cronômetro:
| Busca-em-Profundidade (G) |
| 1 . para cada v em V(G) |
| 2 .ooo cor[v] := branco |
| 3 . t := 0 |
| 4 . para cada r em V(G) |
| 5 .ooo se cor[r] = branco |
| 6 .oooooo pai[r] := r |
| 7 .oooooo DFS-r (G, r) |
| 8 . devolva pai, pré, pós |
Eis a versão apropriada de DFS-r:
| DFS-r (G, v) |
| 19 . cor[v] := cinza |
| 10 . pré[v] := t := t+1 |
| 11 . para cada w em Adj[v] faça |
| 12 .ooo se cor[w] = branco |
| 13 .oooooo pai[w] := v |
| 14 .oooooo DFS-r (G, w) |
| 15 . cor[v] := preto |
| 16 . pós[v] := t := t+1 |
Observe que
pre[v] < pós[v]
para cada vértice v.
O vértice está ativo
,
ou vivo
,
durante o intervalo (pré[v], pós[v]).
Ao final intervalo, v morre
.
Qualquer outro vértice que seja descoberto durante o intervalo
certamente morre antes do fim do intervalo.
Portanto, os intervalos de todos os vértices são encaixados.
A ordem crescente dos números pré dá a permutação dos vértices em pré-ordem. (Ou seja, a permutação (v1, v2, … , vn) dos vértices está em pré-ordem se pré[v1] < pré[v2] < ⋯ <6 pré[vn].) Da mesma forma, a ordem crescente dos números pós dá a permutação dos vértices em pós-ordem.
Exemplo D. Considere novamente o digrafo do exemplo A. O algoritmo Busca-em-Profundidade produz os seguintes vetores pré e pós:
| v] | 0 | 1 | 2 | 3 | 4 | 5 |
| pré[v] | 0 | 1 | 8 | 9 | 3 | 4 |
| pós[v] | 7 | 2 | 11 | 10 | 6 | 5 |
0 2
0/7 8/11
/ \ |
1 4 3
1/2 3/6 9/10
\
5
4/5
Basta examinar o vetor pré para deduzir que
![]() (0, 1, 4, 5, 2, 3) é a permutação dos vértices em pré-ordem.
Da mesma forma, basta examinar o vetor pós para concluir que
(0, 1, 4, 5, 2, 3) é a permutação dos vértices em pré-ordem.
Da mesma forma, basta examinar o vetor pós para concluir que
![]() (1, 5, 4, 0, 3, 2) é a permutação dos vértices em pós-ordem.
(1, 5, 4, 0, 3, 2) é a permutação dos vértices em pós-ordem.
O desenho da floresta DFS à direita reflete a ordem em que a busca em profundidade examinou os vértices. Os valores de pré e pós estão escritos abaixo de cada vértice.
Os vetores pré e pós
permitem decidir facilmente se um dado arco
é de avanço, de retorno, ou cruzado.
Como os intervalos de vida
dos vértices são encaixados,
um arco vw é
(Em outras palavras, vw é de avanço se o intervalo de v contém o intervalo de w, de retorno se o intervalo de v está contido no intervalo de w, e cruzado se o intervalo de v é disjunto do intervalo de w e anterior a ele.) Isso pode ser resumido assim: um arco vw é
se cor[x] = branconas linhas 5 e 12 por
se pré[x] = 0. Implemente essas alterações.