O seguinte algoritmo resolve o problema 5.A por redução ao problema do fluxo máximo:
| LocalmenteMínimo $(G, u, r,s)$ |
| 1 . $(D,u') \larr \text{}$ Dirigido $(G,u)$ |
| 2 . $X \larr \text{}$ EdmondsKarp $(D,u',r,s)$ |
| 3 . devolva $X$ |
A rotina Dirigido troca cada aresta de $G$ por dois arcos antiparalelos. Assim, transforma $G$ num grafo dirigido. Além disso, a rotina define uma tabela $u'$ de capacidades atribuindo a cada arco de $D$ a capacidade da correspondente aresta de $G$.
O algoritmo EdmondsKarp
é a versão
do algoritmo de Ford–Fulkerson
discutida no capítulo 2.
O algoritmo devolve um conjunto $X$ de nós de $D$
tal que o corte $\cutout(X)$ tem capacidade mínima
dentre os que separam
$r$ de $s$ em $(D,u')$.
No grafo capacitado $(G,u)$,
o corte $\cut(X)$ é $(r,s)$- O consumo de tempo do algoritmo
LocalmenteMínimo é
assintoticamente igual
ao do algoritmo de Edmonds–Karp,
ou seja,
igual a $\Oh(n m^2)$,
sendo $n$ o número de nós e $m$ o número de arestas de $G$.
A seguinte caracterização da minimalidade
de um corte localmente mínimo segue
do lema 2.6,
do teorema 2.7,
e do lema 2.5
do capítulo 2:
Lema 5.1 (minimalidade de corte local)
Para qualquer par $(r,s)$ de nós de um grafo capacitado $(G,u)$,
um corte $\cut(X)$ que separa $r$ de $s$
é mínimo se e somente se
existem caminhos
simples
$P_1,\ldots, P_k$ de $r$ a $s$
e números positivos
$\beta_1,\ldots,\beta_k$
tais que
$\sum_{i=1}^k \beta_i = \text{}$ $u(X)$ e
$\sum_{E(P_i) \ni e} \beta_i \leq \text{}$ $u_e$
para cada aresta $e$
de $G$. ■
Podemos dizer que cada caminho $P_i$
conduz $\beta_i$ unidades de fluxo
de $r$ a $s$
e o conjunto de caminhos conduz um fluxo de intensidade $u(X)$.
A desigualdade
$\sum ( \beta_i : P_i \ni e ) \leq u_e$
garante que a quantidade total de fluxo na aresta $e$ não passa de $u_e$
e portanto o fluxo respeita $u$.
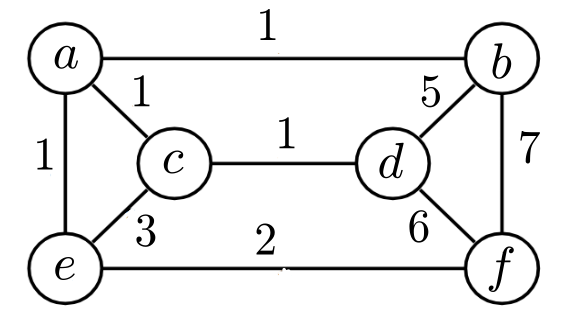
Exemplo 5.1:
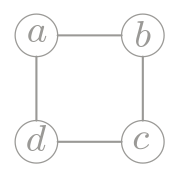
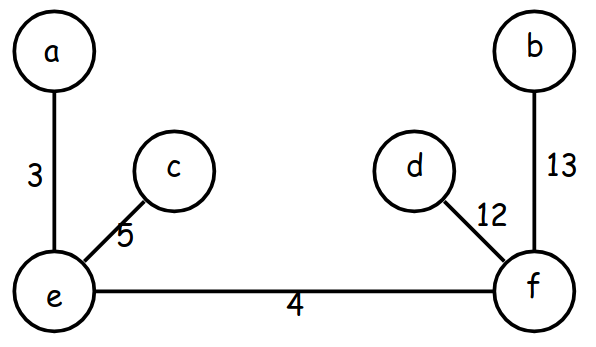
Considere o grafo capacitado representado pela matriz de
adjacências e capacidades abaixo. (Complete a figura.)
O corte $\cut(X)$, com $X:=\conj{a,b,d}$,
separa $d$ de $c$ e tem capacidade $5$.
Os caminhos induzidos por
$(d,c)$,
$(d,b,c)$ e
$(d,a,b,c)$,
conduzindo $2$, $1$ e $2$ unidades de fluxo respectivamente,
satisfazem as condições do lema 5.1.
Portanto, o corte $\cut(X)$ é $(d,c)$-mínimo.
Exemplo 5.2 (árvores):
Seja $(r,s)$ um par de nós de uma
árvore capacitada $(T,u)$
e $P$ o único caminho simples
de $r$ a $s$ em $T$.
Se $a$ é uma aresta de capacidade mínima de $P$
então $\conj{a}$ é um corte $(r,s)$- Podemos resumir este exemplo dizendo que
$\lambda(T,u,r,s) = \text{}$ $\min_{e \in E(P)} u_{e}$,
sendo $P$ o caminho simples de $r$ a $s$ em $T$
e $E(P)$ o conjunto de arestas de $P$.
É importante entender como os cortes
de um grafo interagem.
Dados dois cortes $\cut(X)$ e $\cut(Y)$,
é natural considerar os cortes
$\cut(X\cap Y)$ e $\cut(X\cup Y)$.
Esses quatro cortes satisfazem a seguinte
desigualdade submodular:
Lema 5.3 (desigualdade submodular)
Para quaisquer conjuntos $X$ e $Y$ de nós de um grafo capacitado $(G,u)$
vale a desigualdade
\[
u(X\cap Y)+u(X\cup Y) \leq u(X)+u(Y)\text{.}
\]
[A palavra Prova:
Como $u\geq 0$,
podemos tratar de cada aresta do grafo em separado e
examinar a contribuição que cada uma
dá para cada lado da desigualdade.
Uma aresta $e$ que tem uma ponta em $X\cap\compl{Y}$
e outra em $\compl{X}\cap \compl{Y}$
contribui $u_e$ tanto para o lado esquerdo
quanto para o lado direito da desigualdade.
Uma aresta $e$ com uma ponta em $\compl{X}\cap Y$
e outra em $\compl{X}\cap \compl{Y}$
contribui $u_e$ para o lado esquerdo e $u_e$ para o lado direito.
Uma aresta $e$ de $X\cap Y$ para $\compl{X}\cap Y$
contribui $u_e$ para cada lado.
Uma aresta $e$ de $X\cap Y$ para $X\cap\compl{Y}$
contribui $u_e$ para cada lado.
Uma aresta $e$ de $X\cap Y$ para $\compl{X}\cap \compl{Y}$
contribui $2u_e$ para cada lado.
Finalmente, uma aresta $e$ de $X\cap\compl{Y}$ para $\compl{X}\cap Y$
contribui $0$ para o lado esquerdo e
$2u_e$ para o lado direito da desigualdade. ■
A desigualdade submodular pode ser escrita assim:
$u(X\setm Y)+u(Y\setm X) \leq \text{}$ $u(X)+u(Y)$.
Essa é a versão posi-modular
da desigualdade submodular.
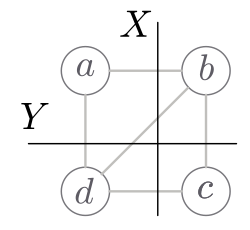
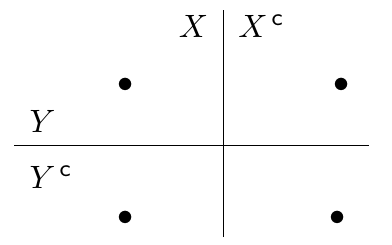
Exemplo 5.3:
A figura mostra conjuntos $X$ e $Y$ de nós de um grafo capacitado $(G,u)$.
Observe a desigualdade submodular
$u(X\cap Y)+u(X\cup Y) = \text{}$ $8 + 5 \leq \text{}$ $9 + 6 = \text{}$
$u(X)+u(Y)$.
A desigualdade submodular permite Lema 5.4
Dados nós $r$, $s$, $p$ e $q$
de um grafo capacitado $(G,u)$,
seja $\cut(X)$ um corte $(r,s)$- Prova:
Como $X\cap Y$ separa $r$ de $s$ e $X\cup Y$ separa $p$ de $q$,
temos $u(X\cap Y) \geq u(X)$
e $u(X\cup Y) \geq u(Y)$.
Assim,
\[
u(X)+u(Y) \leq u(X\cap Y)+u(X\cup Y)\text{.}
\]
Mas $u(X\cap Y)+u(X\cup Y) \leq u(X)+u(Y)$
graças à desigualdade submodular
(lema 5.3).
Portanto, temos
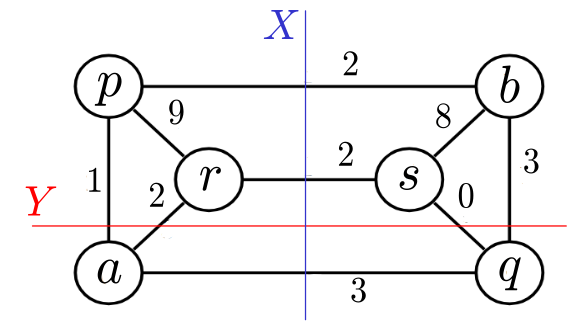
Exemplo 5.4:
No grafo capacitado da figura,
o corte $\cut(X)$ tem capacidade $7$ e o corte $\cut(Y)$ tem capacidade $6$.
O corte $\cut(X)$ é $(r,s)$-
O lema 5.4 tem a seguinte versão posi-modular.
Seja $\cut(X)$ um corte $(r,s)$-
Uma consequência importante do
lema 5.4
é a possibilidades de Lema 5.5 (do descruzamento)
Dados nós $r$ e $s$ de um grafo capacitado $(G,u)$,
seja $\cut(X)$ um corte $(r,s)$- Prova:
Ajuste a notação,
invertendo os papéis de $r$ e $s$ se necessário,
de modo que $r$ esteja em $X$.
Seja $\cut(Y)$ um corte $(p,q)$- Caso 1: $s \in \compl{Y}$.
Nesse caso, $X\cup Y$ separa $r$ de $s$
e $X\cap Y$ separa $p$ de $q$.
De acordo com o lema 5.4,
$\cut(X\cap Y)$ é $(p,q)$- Caso 2: $s \in Y$.
Nesse caso,
$Y\setm X$ separa $s$ de $r$ e
$X\setm Y$ separa $q$ de $p$.
De acordo com a
versão posi-modular do lema 5.4,
$\cut(X \setm Y)$ é $(q,p)$-
O problema central deste capítulo
é encontrar um corte globalmente
mínimo, ou seja,
um corte não trivial
$\cut(X)$ tal que
$u(X) \leq u(X')$
para todo corte não trivial $\cut(X')$.
Convém tratar de um problema mais geral,
que envolve um novo parâmetro:
um conjunto arbitrário $K$ de nós que chamaremos terminais.
Diremos que um conjunto $X$ de nós divide
o conjunto $K$ de terminais
se $X$ separa dois dos terminais.
Em outras palavras, $X$ divide $K$
se $X\cap K\neq \emptyset$ e
$\compl{X}\cap K\neq \emptyset$.
Dizemos também que o corte $\cut(X)$ —
e não só sua margem $X$ —
divide $K$.
Dado um grafo capacitado $(G,u)$ e um conjunto $K$ de terminais,
um corte $C$ é $K$-mínimo
se $C$ divide $K$ e
$u(C) \leq u(C')$ para todo corte $C'$
que divide $K$.
Dizemos que um corte $K$- Problema 5.B (corte globalmente mínimo)
Dado um grafo capacitado $(G,u)$ e um subconjunto $K$ de $V(G)$,
encontrar um corte $K$-mínimo.
Uma instância do problema tem solução
se e somente se $|K| \geq 2$.
O conjunto de instâncias em que $|K| = 2$
é o problema 5.A
(veja a seção 5.1).
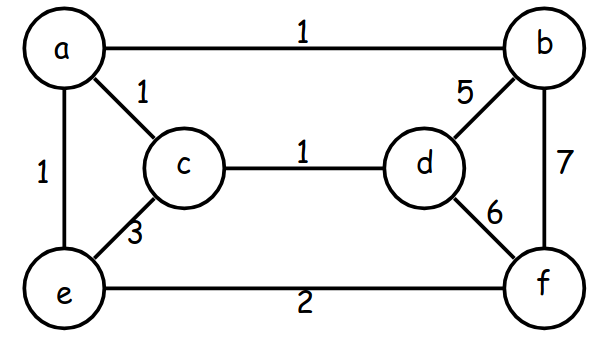
Exemplo 5.5:
No exemplo abaixo, todos os nós são terminais e todas as arestas
têm capacidade $1$.
Todo corte globalmente mínimo tem capacidade $1$.
Exemplo 5.6:
Seja $(T,u)$ um grafo capacitado em que
$T$ é uma árvore.
Seja $K$ um conjunto de dois ou mais terminais
e $a$ uma aresta de capacidade mínima
dentre as que têm ambas as pontas
em $K$.
Então $\conj{a}$ é um corte globalmente mínimo
conforme o exemplo 5.2.
A capacidade de um corte globalmente mínimo em $(G,u,K)$ é denotada por
$\lambda(G,u,K)$.
Se $|K| \lt 2$, adotamos a convenção
$\lambda(G,u,K) := \infty$.
É evidente que $\lambda(G,u,K)$ aumenta quando $K$ encolhe,
ou seja,
$\lambda(G,u,K') \geq \lambda(G,u,K)$
sempre que $K' \subset K$.
A propósito, o número $\lambda(G,1,V(G))$ é conhecido
como aresta-conexidade
(= edge-connectivity) de $G$.
O problema 5.B é
uma união de instâncias do problema 5.A,
uma instância para cada par de terminais.
Assim,
\[
\lambda(G,u,K) = \min_{r,s\,\in\,K}\,\lambda(G,u,r,s)\text{.}
\]
Segue daí que uma instância do problema 5.B
com $t$ terminais pode ser resolvida com
$t(t- 1)/2$
invocações do algoritmo
LocalmenteMínimo
da seção 5.1.
Esse número cresce com o quadrado de $t$,
o que torna o método de solução muito lento.
Gomory e Hu observaram
que a interação
entre os muitos cortes localmente mínimos
(discutida na
seção 5.2),
permite calcular um corte globalmente mínimo com apenas
$t-1$
invocações do algoritmo LocalmenteMínimo.
As próximas seções mostram como fazer isso.
A seguinte consequência do
lema 5.4
contém a essência do algoritmo de Gomory–Hu
mencionado na seção anterior:
Teorema 5.6 (Gomory–Hu)
Seja $(G,u)$ um grafo capacitado,
$K$ um subconjunto de $V(G)$,
$(r,s)$ um par de elementos de $K$,
e $\cut(X)$ um corte $(r,s)$- Prova:
Adote as abreviaturas $\lambda(r,s):=\text{}$ $\lambda(G,u,r,s)$
e $\lambda(K):=\text{}$ $\lambda(G,u,K)$.
Seja $\cut(X)$ um corte $(r,s)$-
Ajuste a notação,
invertendo os papéis de $r$ e $s$ se necessário,
de modo que $r$ esteja em $X$.
Ajuste a notação,
invertendo os papéis de $Y$ e $\compl{Y}$ se necessário,
de modo que $r$ esteja em $Y$.
Sejam $p$ e $q$ dois elementos de $K$ tais que
$\cut(Y)$ é $(p,q)$- Caso 1: $q \in \compl{X}$.
Nesse caso, $X \cap Y$ separa $r$ de $s$ e
$X \cup Y$ separa $p$ de $q$.
De acordo com o
lema 5.4,
$\cut(X \cap Y)$ é $(r,s)$- Caso 2: $q \in X$.
Nesse caso, $Y \setm X$ separa $s$ de $r$ e
$X \setm Y$ separa $q$ de $p$.
De acordo com a
versão posi-modular do lema 5.4,
$\cut(Y \setm X)$ é $(r,s)$-
Algoritmo.
O algoritmo de Gomory–Hu para o problema 5.B
decorre do teorema 5.6.
Ele recebe um grafo capacitado $(G,u)$
com conjunto $K$ de terminais
e usa o método da divisão e conquista
para calcular (uma margem de)
um corte $K$-mínimo.
(Note que,
para a maior parte dos pares $(v,w)$ de nós de $K$,
o algoritmo jamais calcula um corte $(v,w)$-
Exemplo 5.7:
A matriz de adjacências e capacidades abaixo representa um grafo capacitado
$(G,u)$.
Adote o conjunto de terminais $K=V(G)$.
Submeta $(G,u,K)$ ao algoritmo GlobalmenteMínimo.
Tome $r=a$ e $s=b$ na linha 1 do algoritmo.
No fim da linha 2 temos $X=\conj{a,d}$ e $u(X)=9$.
No fim da linha 4 temos $X'=\conj{d}$,
$u(X')=7$ e $\cut(X')$ é $(K\cap X)$- Como $u(X'') \lt u(X') \lt u(X)$,
o algoritmo devolve $X''$ na linha 9.
O corte $\cut(X'')$ é $K$-mínimo
e $\lambda(G,u,K) = 5$.
Exemplo 5.8:
Seja $(G,u)$ o grafo capacitado da figura
(o mesmo do exemplo 5.4)
com conjunto de terminais $K=V(G)$.
No fim da linha 2 do algoritmo temos $X=\conj{a,p,r}$.
O corte $\cut(X)$ é $(r,s)$- No fim da linha 4 temos $X'=\conj{b,p,r,s}$.
(O algoritmo poderia, igualmente bem, ter escolhido $X'=\conj{a}$.)
O corte $\cut(X')$ é $(K\cap X)$- Como $u(X') = u(X'') \lt u(X)$,
o algoritmo devolve $X'$.
O corte $\cut(X')$ é $K$-mínimo.
O corte $\cut(X'')$ também é $K$-mínimo.
Consumo de tempo.
Digamos que $t$ é o número de terminais, ou seja,
$t := |K|$.
Se $f(t)$ é o número máximo de invocações
do algoritmo LocalmenteMínimo
na linha 2
de GlobalmenteMínimo
então $f(1)=0$ e
\[
f(t) = 1 + \max_{t'+t''=t}\left( f(t')+f(t'') \right)
\]
para $t\geq 2$,
sendo $\max$ tomado sobre todos os pares $(t',t'')$
de inteiros positivos tais que $t'+t''=t$.
A solução dessa recorrência é $f(t)=t-1$ para todo $t\geq 1$.
Em outras palavras, o algoritmo GlobalmenteMínimo
faz no máximo
\[
t-1
\]
cálculos de corte localmente mínimo.
Assim, o consumo de tempo de GlobalmenteMínimo
é $\Oh(t\,F(n,m))$,
sendo $F(n,m)$ o consumo de LocalmenteMínimo
para um grafo com $n$ nós e $m$ arestas.
Como $t\leq n$ e $F(n,m)=\Oh(nm^2)$,
podemos dizer que o algoritmo consome $\Oh(n^2m^2)$ unidades de tempo.
Embora execute o subalgoritmo LocalmenteMínimo
apenas $t-1$ vezes,
o algoritmo GlobalmenteMínimo
é lento.
Outros algoritmos
para o problema 5.B
têm o mesmo consumo assintótico mas são mais rápidos
porque a constante escondida sob a notação $\Oh()$ é menor.
O algoritmo GlobalmenteMínimo
da seção anterior
calcula uma certa coleção de cortes localmente mínimos,
ou melhor, uma certa coleção de margens de
cortes localmente mínimos.
Essa coleção é
Suponha que $G$ é um grafo e $T$ um árvore
tal que $V(T)=V(G)$.
(O conjunto de arestas de $T$
não tem relação direta com $E(G)$
e portanto $T$ não é, em geral,
um subgrafo de $G$.)
Dada uma aresta $ij$ de $T$,
seja $R$ o conjunto de nós de qualquer das duas
componentes conexas
de $T-ij$
e considere o corte $\cut(R)$ de $G$.
Diremos que esse corte de $G$ é
induzido por $T-ij$.
Uma árvore de cortes mínimos,
ou árvore de Gomory–Hu,
para um grafo capacitado $(G,u)$
é qualquer árvore $T$ tal que
$V(T)=V(G)$ e,
para cada aresta $ij$ de $T$,
o corte de $G$ induzido por $T-ij$
tem capacidade
$\lambda(G,u,i,j)$.
A segunda condição da definição poderia ser formulada assim:
para cada aresta $ij$ de $T$,
o corte induzido por $T-ij$
é $(i,j)$-
Qualquer árvore $T$ de cortes mínimos para $(G,u)$
descreve uma coleção Lema 5.7
Para qualquer árvore $T$ de cortes mínimos de um grafo capacitado $(G,u)$
e qualquer par $(r,s)$ de nós de $G$,
tem-se
\[\textstyle
\lambda(G,u, r, s) = \min_{ij}\,u(R_{ij})\,,
\]
sendo $\min_{ij}$ tomado sobre todas as arestas $ij$
do caminho simples de $r$ a $s$ em $T$
e $\cut(R_{ij})$ o corte de $G$ induzido por $T-ij$.
Prova:
Seja $P$ o caminho simples de $r$ a $s$ em $T$.
Como já observamos acima,
$\lambda(G, u, r, s) \leq \text{}$ $u(R_{ij})$
para cada aresta $ij$ de $P$.
Portanto, basta mostrar que $\lambda(G, u, r, s) \geq u(R_{pq})$
para alguma aresta $pq$ de $P$.
Seja $\cut(X)$ um corte $(r,s)$-
Para tirar bom proveito computacional do lema,
convém tratar toda árvore de cortes mínimos
como um grafo capacitadado,
sendo $\lambda(G, u, i,j)$ a capacidade
de uma aresta genérica $ij$ da árvore.
Exemplo 5.9:
Seja $(G,u)$ um grafo capacitado em que $G$ é uma árvore.
É fácil verificar que $G$ é uma árvore de cortes mínimos
para $(G,u)$.
Exemplo 5.10:
Seja $(G,u)$ um grafo capacitado em que $G$
consiste em um circuito e nada mais.
Seja $e$ uma aresta de capacidade mínima.
Então $G-e$ é uma árvore de cortes mínimos para $(G,u)$.
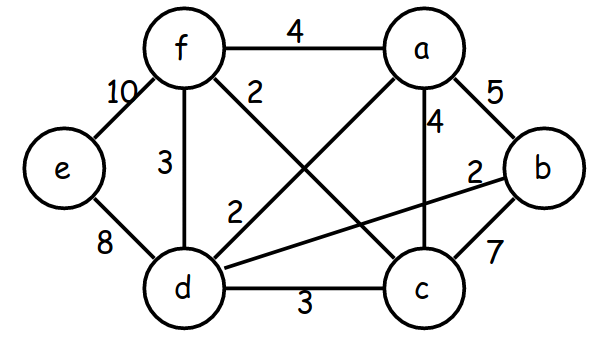
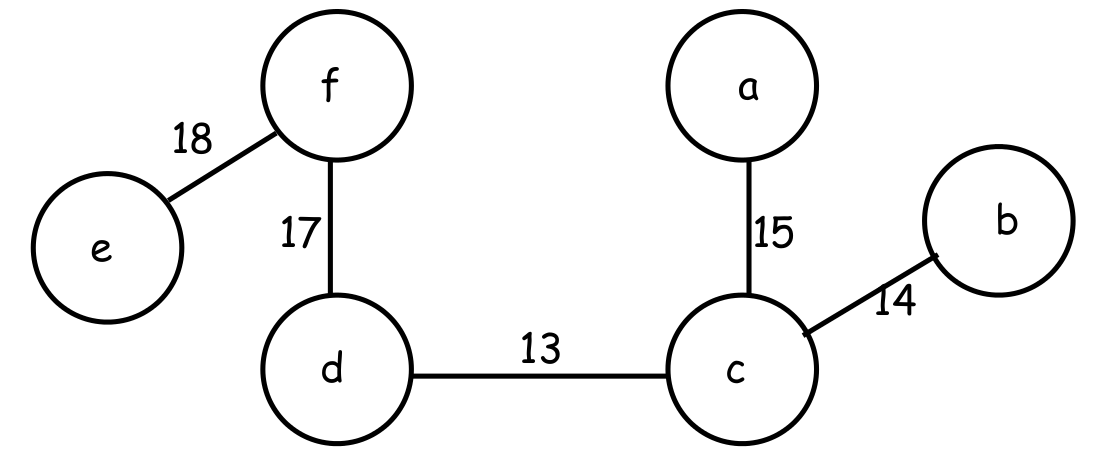
Exemplo 5.11:
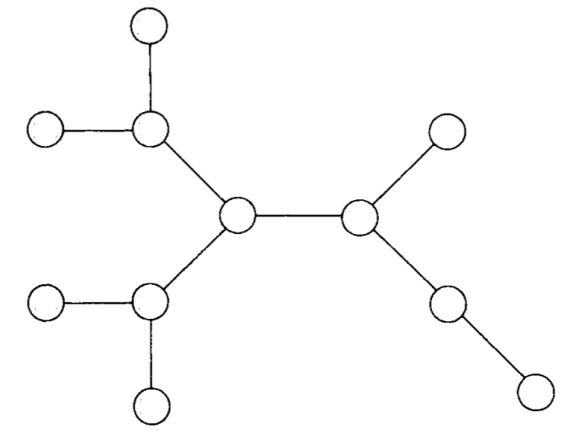
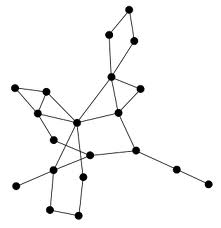
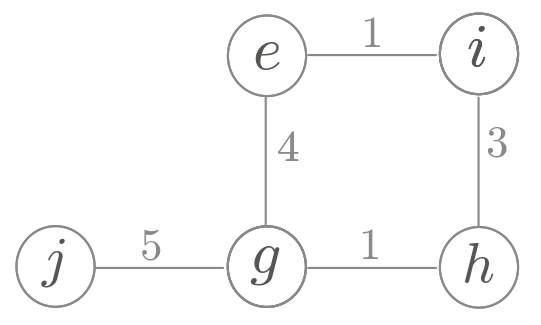
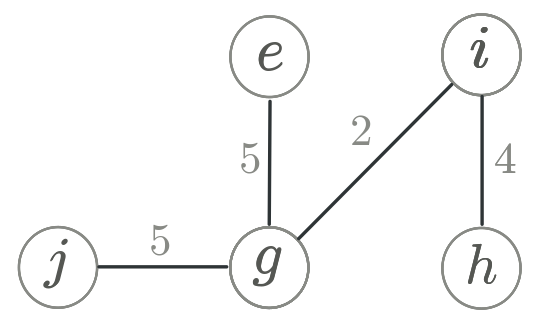
O lado esquerdo da figura mostra um grafo capacitado
$(G,u)$.
O lado direito mostra uma árvore de cortes mínimos
para $(G,u)$.
O número ao lado de cada aresta $ij$ da árvore é
o valor de $\lambda(G,u,i,j)$.
É verdade que todo grafo capacitado tem uma árvore de Gomory–Hu?
A resposta é afirmativa, mas está longe de ser óbvia.
Teorema 5.8 (Gomory–Hu)
Todo grafo capacitado
tem uma árvore de cortes mínimos.
A prova do teorema é um tanto complexa.
Ela envolve uma generalização do conceito de árvore de cortes mínimos
que faremos isso na próxima seção.
Exemplo 5.12:
A tabela descreve uma coleção laminar Esta seção dá uma prova algorítmica do
teorema 5.8.
A prova é indutiva,
sendo a indução feita sobre o tamanho de um conjunto de terminais,
como os que usamos na seção 5.3.
Para fazer isso,
será necessário generalizar
a definição de árvore de cortes mínimos.
O conjunto de terminais do grafo $G$
será denotado por $K$
e o conjunto de nós da árvore de cortes mínimos
será $K$.
Usaremos a expressão
partição indexada por $K$
para designar
qualquer tabela $L$
que associa a cada terminal $k$ um subconjunto $L(k)$ de $V(G)$
e tem as seguintes propriedades:
(É claro que a coleção $\conj{L(k) : k \in K}$
é uma partição
de $V(G)$.)
Dada uma árvore $T$ com $V(T)=K$
e uma aresta $ij$ de $T$,
seja $R$ o conjunto de nós de qualquer uma das duas
componentes conexas
de $T-ij$.
Agora
considere o corte de $G$ cuja margem é
$\bigcup_{k\in R} L(k)$.
Diremos que esse corte é induzido por $T-ij$
e $L$.
Agora que introduzimos a notação e a terminologia apropriada,
podemos formular a definição generalizada de árvore de cortes mínimos.
Dado um grafo capacitado $(G,u)$ e um subconjunto $K$ de $V(G)$,
uma árvore de cortes mínimos
para $(G,u,K)$ é um par $(T,L)$
em que $T$ uma árvore com $V(T) = K$ e $L$ é uma
partição indexada por $K$
tal que,
para cada aresta $ij$ de $T$,
o corte em $(G,u)$ induzido por $T-ij$ e $L$
é $(i,j)$- Podemos agora enunciar a generalização do teorema 5.8
que estabelece
a existência de árvores de cortes mínimos:
Teorema 5.9 (Gomory–Hu)
Para qualquer grafo capacitado $(G,u)$
e qualquer conjunto $K$ de seus nós,
existe uma árvore de cortes mínimos para $(G,u,K)$.
A prova do teorema
é um algoritmo de divisão e conquista
que pode ser grosseiramente resumido assim:
faça uma bipartição $(K',K'')$ de $K$,
encontre uma árvore de cortes mínimos para $(G,u,K')$,
encontre uma árvore de cortes mínimos para $(G,u,K'')$,
e ligue as duas árvores por uma aresta apropriada.
A prova mostrará como construir uma árvore de cortes mínimos
quando $|K|=1$,
como construir uma árvore de cortes mínimos
quando $|K|=2$,
e assim por diante.
Para implementar essa ideia,
precisamos da operação de contração de nós.
Operação de contração.
A contração
(= shrinking)
de um subconjunto
$W$ de $V(G)$
é a operação que produz um novo grafo
em que $W$ é tratado como um nó.
Mais formalmente,
o novo grafo $G'$
tem conjunto de nós $\compl{W}\cup \conj{W}$
e conjunto de arestas definido da seguinte maneira:
para cada aresta $vw$ de $G$ tal que $v\in \compl{W}$,
As arestas de $G$ que têm ambas as pontas em $W$
não estão representadas em $G'$.
Ademais,
$G'$ não tem arestas A contração de $W$ tem o efeito
de eliminar aqueles —
e somente aqueles —
cortes de $G$ que dividem $W$,
ou seja,
aqueles cortes $\cut(Z)$
para os quais $Z\cap W \neq \emptyset$ e
$\compl{Z} \cap W\neq \emptyset$.
Se $G$ tem uma tabela de capacidades $u$,
a definição da correspondente tabela $u'$
para o grafo contraído $G'$ é previsível:
para cada aresta $vW$ de $G'$ tem-se
$u'_{vW} := \text{}$ $\sum \left(u_{vw} : vw\in \cut(W)\right)$
e
para cada aresta $vw$ de $G'$ com ambas as pontas em $\compl{W}$
tem-se
$u'_{vw} := \text{}$ $u_{vw}$.
Com isso,
os cortes de $G'$ têm a mesma capacidade que
os correspondentes cortes de $G$.
Mais precisamente,
para cada subconjunto $Z$ de $V(G')$,
se $Z\not\ni W$ então
\begin{equation}\label{eq:uprime-equals-u}
u'(Z) = u(Z)
\end{equation}
e se $Z\ni W$ então
\begin{equation}\label{eq:uprime-equals-u-generalized}
u'(Z) = u(Z^*)
\end{equation}
sendo $Z^* := (Z \setm \conj{W}) \cup W$
o subconjunto de $V(G)$ que corresponde a $Z$.
Prova do teorema 5.9.
A prova do
teorema 5.9
é uma indução em $|K|$.
A base da indução é o caso em que $|K| = 1$.
Nesse caso,
a árvore de cortes mínimos é o par trivial $(T,L)$
definido por $V(T) := \conj{k}$,
$E(T) := \emptyset$,
e $L(k) := V(G)$,
sendo $k$ o único elemento de $K$.
Suponha agora que $|K| \geq 2$.
Sejam $r$ e $s$ dois nós em $K$ e
seja $\cut(X)$
um corte $(r,s)$-
Seja $K'$
o conjunto $K\cap X$.
Podemos supor, por hipótese de indução, que $(G',u',K')$
tem uma árvore de cortes mínimos $(T',L')$.
Note que o nó $\compl{X}$ de $G'$ não pertence a $K'$.
Seja $k'$ o nó de $K'$
tal que $L'(k') \ni \compl{X}$.
(Nada impede que $k'$
coincida com $r$ ou $s$,
mas isso é irrelevante.)
Seja $K''$ o conjunto $K\cap \compl{X}$.
Podemos supor, por hipótese de indução, que
$(G'',u'',K'')$ tem uma árvore de cortes mínimos $(T'',L'')$.
Seja $k''$ o nó de $K''$
tal que $L''(k'') \ni X$.
Seja $T$ a árvore $T'+T'' + k'k''$.
Seja $L$ a tabela que associa a cada $k$ em $K$ um subconjunto de $V(G)$
da seguinte maneira:
$L(k') := L'(k') \setm \conj{\compl{X}}$
e
$L(k) := L'(k)$ para cada $k$ em $K' \setm \conj{k'}$;
$L(k'') := L''(k'') \setm \conj{X}$
e
$L(k) := L''(k)$ para cada $k$ em $K'' \setm \conj{k''}$.
Mostraremos a seguir que $(T,L)$ é uma árvore de cortes mínimos
para $(G,u,K)$.
É claro que $K'\cup K'' = K$.
É claro também que $V(T)=K$
e que $L$ é uma partição indexada por $K$.
Resta apenas provar que,
para cada aresta $ij$ de $T$,
o corte em $(G,u)$ induzido por $T-ij$ e $L$
é $(i,j)$- Se $Y$ separa $r$ de $s$,
essa desigualdade é óbvia pois $\cut(X)$ é $(r,s)$-
$k' \in \compl{Y}$ ou
$k' \in Y$.
Na segunda alternativa,
$k''$ está necessariamente em $\compl{Y}$.
Assim, a segunda alternativa é equivalente à primeira:
basta intercambiar $X, k', G'$
com $\compl{X}, k'', G''$, respectivamente.
Podemos supor portanto, sem perder generalidade,
que $k' \in \compl{Y}$.
Ajuste a notação,
trocando os papéis de $r$ e $s$ se necessário,
de modo que $r$ esteja em $X$.
Como $r$ e $k'$ estão ambos em $X$,
o lema 5.5 garante que existe
um corte $(r,k')$-
Se $Z \ni r$ então $Z$ separa $r$ de $s$,
donde $u(Z) \geq u(X)$,
o que prova \eqref{eq:desiderata-caso-1}
e assim encerra a discussão do caso $ij=k'k''$.
Agora suponha que $Z \not\ni r$ e portanto
$Z \ni k'$.
Considere a árvore de cortes mínimos $(T',L')$
de $(G',u',K')$.
Seja $P$ o caminho de $r$ a $k'$ em $T'$.
Seja $pq$ uma aresta de $P$
que minimiza a capacidade
do corte induzido
por $T'-pq$ e $L'$
em $(G',u')$.
Seja $R$ a margem desse corte que contém $k'$.
De acordo com a generalização óbvia do
lema 5.7
(com $G', u', T', r, k'$ nos papéis de $G, u, T, r, s$ respectivamente),
o corte $\cut(R)$ é $(r,k')$-
Como $R \ni k'$,
a definição de $k'$
garante que o nó $\compl{X}$ de $G'$
também está em $R$.
Seja $R^*$ o conjunto de nós de $G$ que corresponde a $R$,
isto é, $R^* := (R \setm \conj{\compl{X}}) \cup \compl{X}$.
Então
\[
\begin{split}
u(Y) & \geq u(Z) \\
& = u'(Z) \\
& \geq u'(R) \\
& = u(R^*) \\
& \geq u(X)\text{,}
\end{split}
\]
o que prova \eqref{eq:desiderata-caso-1}.
O primeiro Seja $\cut(Z)$ um corte $(i,j)$- Resta provar a desigualdade
O primeiro Isso conclui a prova de que $(T,L)$ é uma árvore de cortes mínimos
para $(G,u,K)$
e assim encerra a prova do teorema 5.9. ■
Algoritmo.
A prova do teorema teorema 5.9 leva imediatamente ao seguinte algoritmo,
que calcula uma árvore de cortes mínimos para $(G,u,K)$.
Suporemos que a operação de contração está encapsulada
numa rotina Contração
que recebe $(G,u,W)$ e devolve
o resultado $(G',u')$ da contração de $W$ em $(G,u)$.
Tal como o algoritmo GlobalmenteMínimo,
o algoritmo GomoryHuTree
consome $\Oh(|K|\,F(n,m))$ unidades de tempo,
sendo
$n := |V(G)|$, $m := |E(G)|$ e
$F(n,m)$ o consumo de LocalmenteMínimo.
Como $|K| \leq n$ e $F(n,m)=\Oh(nm)$,
o consumo de tempo de GomoryHuTree
é $\Oh(n^2m)$.
Exercícios 5.1
5.2 Submodularidade
submodular
foi inspirada
na igualdade modular
$|X\cap Y| + |X\cup Y| = |X| + |Y|$
que vale para qualquer par $(X,Y)$ de conjuntos.]
descruzar
cortes localmente mínimos:
Dados nós $r$ e $s$ de um grafo capacitado $(G,u)$
e conjuntos $X$ e $Y$
que separam
$r$ de $s$,
se os cortes $\cut(X)$ e $\cut(Y)$ são $(r,s)$-$=$
no lugar de cada $\leq$
e cada $\geq$
.
Em particular, $u(X\cap Y) = u(X)$ e $u(X\cup Y) = u(Y)$.
Segue daí que $\cut(X\cap Y)$ é $(r,s)$-descruzar
dois cortes localmente mínimos:
Exercícios 5.2
5.3 Corte globalmente mínimo
Exercícios 5.3
5.4 Algoritmo para corte globalmente mínimo
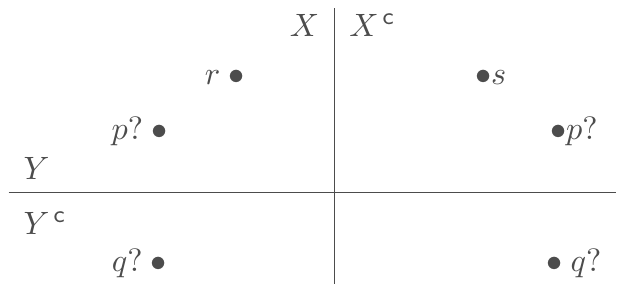
GlobalmenteMínimo $(G,u,K)$
$\rhd$ $|K| \geq 2$
1
.
sejam $r$ e $s$ dois nós de $K$
2
.
$X \larr \text{}$ LocalmenteMínimo $(G,u,r,s)$
3
.
se $|K\cap X| \geq 2$
4
.ooo
então $X' \larr \text{}$ GlobalmenteMínimo $(G,u, K\cap X)$
5
.ooo
então se $u(X') \lt u(X)$ então $X\larr X'$
6
.
se $|K\cap \compl{X}| \geq 2$
7
.ooo
então $X'' \larr \text{}$ GlobalmenteMínimo $(G,u, K\cap \compl{X})$
8
.ooo
então se $u(X'') \lt u(X)$ então $X\larr X''$
9
.
devolva $X$
Exercícios 5.4
$|K| \geq 2$
.
5.5 Árvores de cortes mínimos
completa
no seguinte sentido:
para cada par $(r,s)$ de nós do grafo,
existe um (e apenas um) conjunto $X$ na coleção
tal que o corte $\cut(X)$ é
$(r,s)$-completa
de
cortes localmente mínimos,
como passamos a mostrar.
Sejam $r$ e $s$ dois nós de $G$ e $P$ o
único caminho simples
de $r$ a $s$ em $T$.
Para cada aresta $ij$ de $P$,
seja $\cut(R_{ij})$ o corte induzido em $G$ por $T-ij$.
É óbvio que $\cut(R_{ij})$ separa $r$ de $s$
e portanto $\lambda(G,u,r,s) \leq u(R_{ij})$.
É menos óbvio que temos $=$
no lugar de $\leq$
para alguma aresta $ij$:
completa
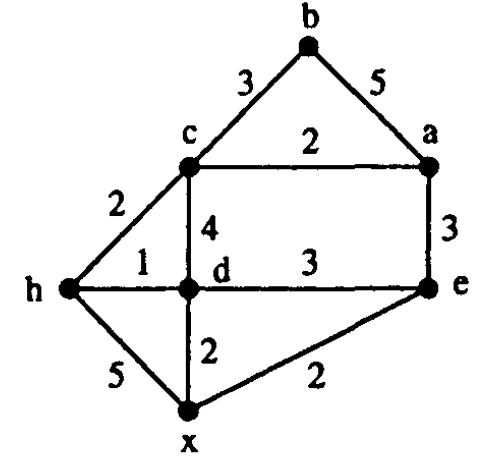
para o grafo capacitado $(G,u)$ da figura.
A coleção pode ser representada pela expressão
$((((b)\ a)\ c)\ (e)\ ((h)\ x)\ d)$.
Converta essa expressão no desenho de uma árvore de cortes mínimos.
[CCPS 3.71]
Exercícios 5.5
5.6 Algoritmo para árvore de cortes mínimos
paralelas
:
mesmo que $G$ tenha arestas $vw$ e $vw'$ com $v$ em $\compl{W}$ e
$w$ e $w'$
ambos em $W$,
o grafo $G'$
terá uma só aresta $vW$.
$\geq$
segue
de \eqref{eq:uY-geq-uZ}.
O primeiro $=$
segue
de \eqref{eq:uprime-equals-u} pois
$Z \subseteq X$.
O segundo $\geq$
vale porque
$Z$ separa $r$ de $k'$,
enquando $\cut(R)$ é um corte $(r,k')$-$=$
vale em virtude
de \eqref{eq:uprime-equals-u-generalized},
com $R$ no papel de $Z$.
O terceiro $\geq$
vale porque
$R^*$ separa $r$ de $s$
(uma vez que $r\notin R$ e $r \notin \compl{X}$
enquanto $s \in \compl{X}$)
enquanto
$\cut(X)$ é $(r,s)$-$\leq$
.
O corte $\cut(R)$ é $(i,j)$-$=$
vale em virtude
de \eqref{eq:uprime-equals-u},
com $R$ no papel de $Z$,
pois $R \subseteq X \subseteq V(G')$.
O primeiro $\leq$
vale porque $\cut(R)$ é $(i,j)$-$=$
vale em virtude
de \eqref{eq:uprime-equals-u}
pois $Z \subseteq X \subseteq V(G')$.
GomoryHuTree $(G, u, K)$
$\rhd$ $|K| \geq 1$
01
.
se $|K| = 1$
02
.ooo
então seja $k$ o elemento de $K$
03
.ooo
então $T\larr (\conj{k},\emptyset)$
04
.ooo
então $L(k) \larr V(G)$
05
.ooo
então devolva $(T,L)$ e pare
06
.
sejam $r$ e $s$ dois nós de $K$
07
.
$X \larr \text{}$ LocalmenteMínimo $(G,u,r,s)$
08
.
$(G',u') \larr \text{}$ Contração $(G,u,\compl{X})$
09
.
$K' \larr K \cap X$
10
.
$(T',L') \larr \text{}$ GomoryHuTree $(G',u',K')$
11
.
seja $k'$ o nó de $K'$ tal que $L'(k') \ni \compl{X}$
12
.
$(G'',u'') \larr \text{}$ Contração $(G,u,X)$
13
.
$K'' \larr K \cap \compl{X}$
14
.
$(T'',L'') \larr \text{}$ GomoryHuTree $(G'',u'',K'')$
15
.
seja $k''$ o nó de $K''$ tal que $L''(k'') \ni X$
16
.
$T \larr T' + T'' + k'k''$
17
.
$L(k') \larr L'(k') \setm \conj{\compl{X}}$
18
.
para cada $k$ em $K' \setm \conj{k'}$
19
.ooo
$L(k) \larr L'(k)$
20
.
$L(k'') \larr L''(k'') \setm \conj{X}$
21
.
para cada $k$ em $K'' \setm \conj{k''}$
22
.ooo
$L(k) \larr L''(k)$
23
.
devolva $(T, L)$ e pare
Exercícios 5.6