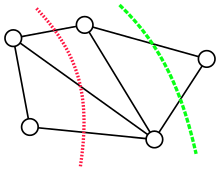
Suponha que quero desconectar uma rede de comunicações cortando alguns links da rede. Quantos links preciso cortar, no mínimo? Quais links preciso cortar? Este é o problema do corte globalmente mínimo.
Esta página discute um algoritmo probabilístico (= aleatorizado = randomized) para o problema do corte globalmente mínimo em um grafo.
A página é baseada na seção 13.2 de Kleinberg e Tardos e na seção 10.2 de Motwani e Raghavan.
Considere um grafo G com conjunto V de vértices e conjunto A de arestas. Dados dois subconjuntos X e Y de V, o conjunto de todas as arestas que têm uma ponta em X e outra ponta em Y será denotado por
A(X, Y).
(Compare com o conceito de corte orientado em um digrafo.) É claro que A(X, Y) é vazio se X ou Y forem vazios. É claro também que A(X, Y) = A(Y, X). Em geral, teremos Y = X, sendo X o complemento de X. Se A(X, X) é diferente de vazio para todo subconjunto não trivial de V então o grafo é conexo. Aqui, como no resto do capítulo, os subconjuntos triviais de V são { } e V.
Um corte é qualquer par (X, X) em que X é um subconjunto não trivial de V. O tamanho de um corte (X, X) é a cardinalidade de A(X, X).
Um corte (X, X)
é mínimo
se o grafo não tem um corte de tamanho menor.
(Usa-se também a expressão corte globalmente mínimo
.
O tamanho de um corte globalmente mínimo
é uma boa medida da robustez
do grafo.)
Problema do corte mínimo em grafos: Encontrar um corte mínimo num grafo.
Para resolver o problema num grafo com n vértices,
poderíamos escolher o menor de
n − 1
cortes localmente
mínimos,
sendo cada um desses cortes calculado pelo
algoritmo Max-Flow-Min-Cut.
Mas nesta página vamos discutir
um interessante algoritmo probabilístico para o problema.
A discussão desse algoritmo servirá de introdução
à classe de algoritmos que usam números aleatórios.
David Karger descobriu (1993)
uma solução probabilística para o problema,
ou seja,
um algoritmo
que usa uma fonte de
números aleatórios
(= random numbers).
O algoritmo de Karger
produz um corte que
pode não ser mínimo,
mas é mínimo com alta probabilidade.
(Em outras palavras, a probabilidade de um falso positivo
é muito baixa.
Esse tipo de algoritmo probabilístico é conhecido como
Monte Carlo.)
O algoritmo de Karger pode ser descrito grosseiramente assim: enquanto o grafo tiver dois ou mais vértices, contraia uma aresta escolhida aleatoriamente. Para lidar com a operação de contração de arestas, precisamos introduzir os conceitos de supervértice e aresta externa. Considere uma partição Π do conjunto de vértices do grafo. Cada elemento de Π é um supervértice. Uma aresta do grafo é interna a Π se tem ambas as pontas num mesmo supervértice e externa a Π se tem pontas em supervértices diferentes. O número de arestas externas a Π é igual à soma
| ½ ∑P∈Π ⎮A(P, P)⎮. | (*) |
O algoritmo de Karger para o problema do corte mínimo recebe um grafo com n ≥ 2 vértices e devolve um corte que é mínimo com probabilidade maior que 2/n². Essa probabilidade é muito baixa, mas se o algoritmo for executado n² vezes, o menor dos cortes produzidos terá probabilidade de 63% de ser mínimo. E a probabilidade aumenta se o algoritmo for executado mais vezes.
Para simplificar a descrição do algoritmo, suporemos que o grafo é conexo. Suporemos também que o grafo tem 2 ou mais vértices, pois do contrário o problema não tem solução.
O algoritmo é iterativo e cada iteração começa com um conjunto de supervértices, ou seja, com uma partição Π do conjunto de vértices do grafo. No começo da primeira iteração, cada supervértice contém um só vértice. O processo iterativo consiste no seguinte:
| enquanto Π tiver 2 ou mais supervértices, |
| .oo escolha aleatoriamente uma aresta a externa a Π, |
| .oo seja P o supervértice que contém uma ponta de a, |
| .oo seja Q o supervértice que contém a outra ponta de a, |
| .oo troque P e Q por P ∪ Q; |
| seja X um elemento de Π e |
| devolva o corte (X, X). |
A operação troque P e Q
por P ∪ Q
consiste em trocar Π por (Π − { P, Q }) ∪
{ P ∪ Q }.
Essa operação é
a contração da aresta a.
Cada contração subtrai 1 da cadinalidade de Π.
Assim,
se o grafo tem n vértices
então,
depois de n − 2 iterações,
Π é reduzida a uma bipartição do conjunto de vértices.
Em cada iteração, a aresta a é escolhido de maneira aleatória uniforme. Em outras palavras, se k é o número de arestas externas então cada aresta externa tem probabilidade 1/k de ser escolhida.
| Corte-Aleatório (V, A) |
| 1 . X := { } |
| 2 . para cada v em V faça |
| 3 .ooo se Rand ( ) = 1 |
| 4 .oooooo então X := X ∪ { v } |
| 5 . devolva X |
Rand é uma fonte de bits aleatórios que produz 0 com probabilidade ½ e 1 com probabilidade ½.
Mostraremos que o corte devolvido pelo algoritmo de Karger é mínimo com probabilidade pelo menos 2/(n² − n), sendo n o número de vértices do grafo. Mais especificamente, dado um corte mínimo (K, K), vamos mostrar que algoritmo devolve (K, K) ou (K, K) com probabilidade não inferior a 2/(n²−n).
Digamos que uma iteração é um fracasso se a aresta a pertence ao conjunto A(K, K). Do contrário, a iteração é um sucesso. Depois de um fracasso, a partição Π deixa de ser um refinamento da bipartição { K, K } do conjunto V de vértices. Enquanto não ocorrerem fracassos, Π segue sendo um refinamento de { K, K }. Para que o algoritmo devolva (K, K) ou (K, K), é preciso que todas as iterações sejam sucessos.
Suponha que Π é um refinamento de { K, K } no início de uma iteração qualquer. Seja k a cardinalidade de A(K, K) e F o conjunto das arestas externas a Π. Então ⎮A(P, P)⎮ ≥ k para todo P em Π e, de acordo com (*),
| ⎮F⎮ ≥ ½ k ⎮Π⎮. | (**) |
A probabilidade de que uma das k arestas do conjunto A(K K) seja escolhida na presente iteração é k / ⎮F⎮. Em virtude de (**), essa probabilidade não passa de
| 2 | . |
| ⎮Π⎮ |
(Note que a probabilidade não depende de k.) Portanto, a probabilidade de que uma iteração seja um sucesso é de pelo menos 1 − 2/⎮Π⎮. A sequência de valores de ⎮Π⎮ ao longo de sucessivas iteraçoes é n, n−1, n−2, etc.. Portanto, a probabilidade de sucessivos sucessos é de pelo menos
| (1 − | 2 | ) (1 − | 2 | ) (1 − | 2 | ) ⋯ (1 − | 2 | ) (1 − | 2 | ) . |
| n | n−1 | n−2 | 4 | 3 |
Esse produto é igual ao quociente de (n−2)(n−3) ⋯ (3)(2)(1) por (n)(n−1) ⋯ (5)(4)(3), que é igual a 2/(n(n−1)). Portanto, a probabilidade de que todas as iterações sejam sucessos é de pelo menos
| 2 | , |
| n² − n |
como queríamos mostrar. Embora muito pequena, esta probabilidade é útil, como veremos na próxima seção.
O algoritmo de Karger encontra um corte mínimo com probabilidade tanto menor quanto maior for n. Gostaríamos de aumentar essa probabilidade de modo que ela não mais dependa de n ou, melhor ainda, aumente com n. Para obter esse efeito, basta executar o algoritmo cerca de n² vezes e escolher o menor dos cortes encontrados. É o que mostraremos a seguir.
Se o algoritmo for executado N vezes e a melhor resposta for escolhida, a probabilidade de não obter um corte mínimo não passará de
| (1 − | 2 | ) N . |
| n² − n |
Como se sabe, (1 − 1/N)N < 1/e para todo N, sendo e ≅ 2.71828 o número de Euler. Portanto, a probabilidade de não obter um corte mínimo depois de (n²−n)/2 repetições do algoritmo é menor que 1/e, ou seja, menor que 37%. A probabilidade de obter um corte mínimo é maior que 63%. Conseguimos assim obter uma probabilidade que não depende de n.
Podemos melhorar nossas chances ainda mais se executarmos o algoritmo cerca de n² ln n vezes. Feito isso, a probabilidade de não obter um corte mínimo será menor que (1/e)ln n = 1/n. A probabilidade de obter um corte mínimo será então maior que
| n − 1 | . |
| n |
A descrição do algoritmo de Karger que fizemos acima está num nível de abstração um tanto alto. Para implementar o algoritmo de maneira eficiente é preciso responder às seguintes questões: como representar os supervértices? como manter atualizado o conjunto F de arestas externas? como escolher uma aresta externa com probabilidade uniforme?
Segue uma implementação simples e um tanto grosseira do algoritmo. Os supervértices são representados por cores: dois vértices têm a mesma cor se e somente se pertencem ao mesmo supervértice.
Vamos supor que o grafo tem vértices 1, 2, … , n e que as arestas estão todas armazenadas (em ordem arbitrária) num vetor F[1 .. m]. Suporemos também, como já fizemos acima, que o grafo é conexo e tem pelo menos 2 vértices.
| 1Karger (n, m, F) |
| 11 . para v de 1 até n |
| 12 .ooo cor[v] := v |
| 13 . n′ := n |
| 14 . m′ := m |
| 15 . enquanto n′ > 2 |
| 16 .ooo a := Random (1, m′) |
| 17 .ooo sejam p e q as pontas de F[a] |
| 18 .ooo para v de 1 até n |
| 19 .oooooo se cor[v] = cor[q] |
| 10 .ooooooooo cor[v] := cor[p] |
| 11 .ooo n′ := n′ − 1 |
| 12 .ooo m″ := 0 |
| 13 .ooo para b de 1 até m′ |
| 14 .oooooo sejam v e w as pontas de F[b] |
| 15 .oooooo se cor[v] ≠ cor[ w] |
| 16 .ooooooooo m″ := m″ + 1 |
| 17 .ooooooooo F[m″] := F[b] |
| 18 .ooo m′ := m″ |
| 19 . X := {1} |
| 20 . para v de 2 até n |
| 21 .ooo se cor[v] = cor[1] |
| 22 .oooooo X := X ∪ { v } |
| 23 . devolva (X, X) |
O valor de n′ é o número de cores, ou seja, o número de supervértices. O valor de m′ é o número de arestas externas à partição descrita por cor. O comando Random (1, m′) produz um elemento do intervalo 1 .. m′ com probabilidade uniforme, ou seja, com probabilidade 1/m′ para cada elemento.
Desempenho. O processo iterativo principal (bloco de linhas 5-18) é repetido n − 2 vezes. Vamos supor que a linha 6 pode ser executada em Ο(1) unidades de tempo. (Acho que Ο(lg m′) seria mais realista.) Cada execução do bloco de linhas 8-10 consome Ο(n) unidades de tempo. Cada execução do bloco de linhas 13-17 consome Ο(m) unidades de tempo. Como isso, o consumo de tempo total do algoritmo fica em
Ο(n(n + m))
unidades de tempo. Como estamos supondo que o grafo é conexo, temos n ≤ m+1 e portanto o tempo está em Ο(n m).
Se o algoritmo for executado n² lg n vezes, o consumo de tempo total estará em Ο(n³ m lg n). (Infelizmente, isso não chega a competir com a solução determinística que consiste em executar o algoritmo max-flow-min-cut n − 1 vezes.)
A implementação dos supervértices poderia ser melhorada com uma estrutura de dados do tipo union-find. É mais difícil melhorar a administração do conjunto de arestas externas de modo que ela consuma menos tempo. Mas existem implementações do algoritmo de Karger que são mais rápidas que a exibida acima.