Esta página introduz o conceito de componente forte de um digrafo e discute um algoritmo que usa busca em profundidade para encontrar as componentes fortes.
A solução de muitos problemas sobre digrafos usa a seguinte estratégia de divisão e conquista: primeiro, resolve o problema em cada componente forte; depois, costura as soluções parciais para obter uma solução global.
Esta página é inspirada na seção 22.5 do CLRS.
Um digrafo é fortemente conexo (= strongly connected) se, para cada par (v, w) de seus vértices, existe um caminho de v a w e um caminho de w a v. Em outras palavras, um digrafo é fortemente conexo se qualquer vértice está ao alcance de qualquer outro.
Problema da conexão forte: Decidir se um digrafo é fortemente conexo.
Parece fácil resolver o problema: basta verificar, para cada vértice v, se todos os demais vértices estão ao alcance de v. E isso pode ser feito com n buscas (em largura ou em profundidade), uma busca para cada um dos n vértices do digrafo. Mas esse algoritmo é muito lento: consome Θ(n³) unidades de tempo no pior caso. O algoritmo é ineficiente porque cada uma das n buscas refaz boa parte do trabalho da busca anterior.
É possível resolver o problema com apenas duas buscas se estivermos dispostos a construir o transposto do digrafo, ou seja, um novo digrafo que tem um arco wv para cada arco vw do digrafo original. Será possível resolver o problema com apenas uma busca?
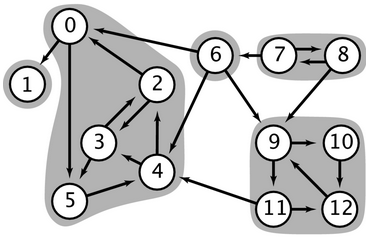
Exemplo A. O digrafo representado na figura à direita não é fortemente conexo. Dê uma evidência simples e convincente desse fato.
Todo digrafo é um mosaico de subdigrafos fortemente conexos. Cada peça do mosaico é conhecida como componente forte do digrafo. Mais precisamente, uma componente forte (= strong component) de um digrafo é um subdigrafo fortemente conexo maximal. Portanto, um subdigrafo fortemente conexo F de um digrafo G é uma componente forte se e somente se não existe digrafo fortemente conexo F′ tal que F ⊂ F′ ⊆ G.
Há uma relação íntima entre componentes fortes e ciclos. Todo ciclo de um digrafo pertence a alguma componente forte. Por outro lado, todo arco de qualquer componente forte pertence a um ciclo.
Problema das componentes fortes: Encontrar as componentes fortes de um digrafo.
Para representar uma solução do problema, podemos atribuir rótulos aos vértices de modo que vértices de uma mesma componente forte tenham rótulos iguais e vértices de componentes fortes diferentes tenham rótulos diferentes.
Num digrafo acíclico, cada componente forte tem um só vértice. Reciprocamente, se cada componente forte de um digrafo tem um só vértice então o digrafo é acíclico. Essa observação sugere a introdução do conceito de digrafo das componentes fortes.
O digrafo das componentes fortes de um digrafo G, digamos D(G), é definido assim: os vértices de D(G) são as componentes fortes de G e há um arco EF em D(G) se E e F são componentes distintas e existe um arco em G com ponta inicial em E e ponta final em F. É fácil verificar que
D(G) é acíclico,
ou seja, um DAG. Por isso, D(G) também é conhecido como núcleo acíclico (= kernel dag) do digrafo G. Podemos dizer, informalmente, que todo digrafo é um conjunto de digrafos fortemente conexos interligados por um DAG.
Como se sabe, todo DAG admite uma permutação topológica. Ademais, uma tal permutação topológica é revelada por uma busca em profundidade. Essas observações serão exploradas nas próximas seções para construir um algoritmo que resolve o problema das componentes fortes.
S. R. Kosaraju descobriu (1978) um algoritmo muito eficiente para resolver o problema das componentes fortes. (O algoritmo também foi descoberto por M. Sharir.) Ao receber um digrafo G, o algoritmo de Kosaraju atribui um rótulo sc[v] a cada vértice v de G de tal modo que sc[v] = sc[w] se e somente se v e w estão na mesma componente forte de G. (O nome do vetor de rótulos é uma abreviatura de strong component.)
O algoritmo de Kosaraju faz duas buscas em profundidade: uma no digrafo G outra no transposto de G, isto é, no digrafo GT que tem os mesmos vértices de G e um arco wv para cada arco vw de G. (A matriz de adjacência de GT é a transposta da matriz de adjacência de G.) O digrafo GT tem essencialmente as mesmas componentes fortes que G.
| Kosaraju (G) |
| 11 . n := ⎮V(G)⎮ |
| 12 . pós := Busca-em-Profundidade (G) |
| 13 . u[1 .. n] := Permuta-Vértices (pós) |
| 14 . GT := Transposto (G) |
| 15 . para cada v em V(G) |
| 16 .ooo sc[v] := 0 |
| 17 . j := 0 |
| 18 . para i := n decrescendo até 1 |
| 19 .ooo se sc[u[i]] = 0 ▷ nova etapa da busca |
| 10 .oooooo j := j + 1 |
| 11 .oooooo SC-DFS-r (GT, u[i], sc, j) |
| 12 . devolva sc |
O algoritmo tem duas fases. A primeira fase corresponde ao bloco de linhas 1-3 e a segunda fase ao bloco de linhas 4-11. Na linha 2, o algoritmo faz uma busca em profundidade no digrafo G e produz o vetor pós de numeração dos vértices em pós-ordem. Na linha 3, a rotina Permuta-Vértices converte o vetor pós na permutação (u[1], u[2], … , u[n]) dos vértices de G em pós-ordem.
Agora considere a fase 2. Na linha 4, a rotina Transposto constrói o transposto GT do digrafo G. (Mostraremos abaixo que (u[1], u[2], … , u[n]) é, essencialmente, uma permutação topológica do DAG das componentes fortes de GT.) O bloco de linhas 5-11 processa os vértices de GT na ordem u[n], u[n−1], … , u[1] para rotular as componentes fortes de GT, e portanto também as de G. Esse bloco de linhas é uma variante do código de Busca-em-Profundidade. Em particular, a rotina SC-DFS-r é uma variante do código de DFS-r.
| SC-DFS-r (H, v, sc, j) |
| 13 . sc[v] := j |
| 14 . para cada w em Adj[v] |
| 15 .ooo se sc[w] = 0 |
| 16 .oooooo SC-DFS-r (H, w, sc, j) |
(É claro que Adj na linha 14 é o vetor de listas de adjacência de H.) Cada execução de SC-DFS-r atribui rótulo j a cada vértice w de H que esteja ao alcance de v e ainda não tenha recebido um rótulo.
(A maneira como é feita a busca na fase 2 não é crítica. A rotina SC-DFS-r faz busca em profundidade, mas poderia igualmente bem ter feito busca em largura. Veja exercício abaixo.)
Exemplo B. Seja G o digrafo definido pelas listas de adjacência abaixo. (Exemplo copiado da figura 22.9 de CLRS.)
| v | Adj[v] |
| a | (b) |
| b | (c, e, f) |
| c | (d, g) |
| d | (c, h) |
| e | (a, f) |
| f | (g) |
| g | (f, h) |
| h | ( ) |
Veja o resultado da busca em profundidade no digrafo G começando pelo vértice c (os vértices estão listados na ordem em que foram descobertos):
| v] | c | g | f | h | d | b | e | a |
| pré[v] | 1 | 2 | 3 | 5 | 8 | 11 | 12 | 13 |
| pós[v] | 10 | 7 | 4 | 6 | 9 | 16 | 15 | 14 |
Portanto, (f, h, g, d, c, a, e, b) é a permutação dos vértices de G em pós-ordem. A busca no digrafo transposto GT, seguindo o inverso da ordem (f, h, g, d, c, a, e, b), produz a seguinte rotulação das componentes fortes:
| v] | b | a | e | c | d | g | f | h |
| sc[v] | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 |
(Na primeira linha da tabela, os vértices estão listados na ordem em que foram descobertos.)
Desempenho. Uma análise semelhante à que fizemos na página Ciclos e digrafos acíclicos mostra que o algoritmo Kosaraju consome tempo
Θ(n+m),
sendo n o número de vértices e m o número de arcos do digrafo. Portanto, o algoritmo é linear.
fonteno DAG das componentes de G, ou seja, mostre que nenhum arco de G entra em F. Deduza daí que FT é um
sorvedourono DAG das componentes de GT, ou seja, deduza que nenhum arco de GT sai de FT.
limpado código de Kosaraju trocando u[1 .. n] por uma pilha. Primeiro, escreva uma variante de Busca-em-Profundidade que coloque os vértices numa pilha à medida que eles ficam pretos (última linha de DFS-r). Use essa variante de Busca-em-Profundidade no lugar do par de linhas 2-3. No lugar da linhas 8, desempilhe os vértices da pilha.
Para provar que o algoritmo Kosaraju está correto, basta mostrar que cada invocação de SC-DFS-r na linha 11 do algoritmo rotula uma nova componente forte do digrafo GT (e portanto também uma nova componente forte de G).
Cada invocação de SC-DFS-r na linha 11 resulta numa busca no digrafo GT a partir de um vértice u[i]. Digamos que F é a componente forte de G que contém u[i], e portanto FT é a componente forte de GT que contém u[i]. Precisamos provar que a busca em GT a partir de u[i] descobre todos os vértices de FT e somente esses. Eis as duas partes da prova:
Para concluir a prova da correção do algoritmo de Kosaraju, precisamos apenas tratar da seguinte relação entre as componentes fortes e a permutação dos vértices em pós-ordem de um digrafo:
Propriedade da Pós-Ordem: Considere uma busca em profundidade em um digrafo G e seja (u[1], u[2], … , u[n]) a correspondente permutação dos vértices em pós-ordem. Para qualquer componente forte F de G e qualquer vértice r fora de F, se existe um arco de r a F então r aparece em (u[1], u[2], … , u[n]) depois de todos os vértices de F.
(Observe que r pertence a uma componente forte diferente de F. Podemos dizer então, a grosso modo, que a propriedade afirma o seguinte: a permutação em pós-ordem de G é uma permutação anti-topológica do digrafo das componentes fortes de G.)
Prova da propriedade: Sejam pré e pós as numerações dos vértices produzidas pela busca. (É claro que pós[u[1]] < ⋯ < pós[u[n]].) Seja s um vértice qualquer de F. Para provar a propriedade, basta mostrar que pós[r] > pós[s].
Suponha primeiramente que pré[r] < pré[s], ou seja, a busca descobriu r antes de s. Como F é uma componente forte e existe um arco de r a F, concluímos que s está ao alcance de r. Portanto, s foi descoberto e morreu durante o intervalo (pré[r], pós[r]). Em outras palavras, r é ancestral de s na floresta DFS. Logo, pós[r] > pós[s], como queríamos mostrar.
Suponha agora que pré[r] > pré[s], ou seja, a busca descobriu r depois de s. Observe que r não está ao alcance de s, uma vez que (1) r não pertence a F, (2) existe um arco de r a F, e (3) F é uma componente forte. Logo, r não é descendente de s na floresta DFS. Portanto, o intervalo (pré[r], pós[r]) começou depois do fim do intervalo (pré[s], pós[s]). Segue daí que pós[r] > pós[s], como queríamos mostrar.
Isso conclui a prova de Propriedade da Pós-Ordem e portanto também a prova da correção do algoritmo de Kosaraju.