Esta página discute um algoritmo para o cálculo da distância entre dois vértices em um digrafo. O algoritmo é uma importante aplicação da estratégia de busca em largura.
Esta página é inspirada na seção 2 do capítulo 22 de CLRS e CLRS.
O comprimento (= length) de um caminho em um digrafo é o número de arcos do caminho. A distância de um vértice r a um vértice s é o comprimento de um caminho de comprimento mínimo dentre os que começam em r e terminam em s.
A distância de r a s é infinita
se não existe caminho algum de r a s,
ou seja, se s não está ao alcance de r.
Se c é um número, a afirmação
a distância de r a s é c
equivale a duas afirmações:
(1) existe um caminho de r a s
cujo comprimento é c e
(2) não existe caminho de r a s cujo comprimento
é menor que c.
Problema das distâncias: Dado um vértice r de um digrafo, encontrar a distância de r a cada um dos demais vértices.
Convém insistir em quatro pontos óbvios:
1. A distância de r a s é um número
e não um caminho.
2. Não faz sentido dizer distância mínima
,
pois a distância já é mínima por definição.
3. Em virtude do caráter orientado dos caminhos,
é melhor dizer distância de um vértice a outro
que distância entre dois vértices
.
4. Em geral, a distância de r a s
é diferente da distância de s a r.
A solução do problema pode ser armazenada num vetor dist indexado pelos vértices de modo que dist[v] seja a distância de r a v. É claro que dist[r] = 0.
Exemplo A. Veja as distâncias a partir do vértice 3 no digrafo da figura:
| v] | 1 | 2 | 3 | 4 | 5 | 6 |
| dist[v] | 2 | 1 | 0 | 1 | 2 | 1 |
Nossa primeira descrição de um algoritmo para o problema será feita num nível abstração bastante alto. O algoritmo é iterativo e cada iteração começa com um vetor dist[ ] indexado pelos vértices do digrafo. No começo da primeira iteração, dist[r] vale 0 e dist[w] vale ∞ para todo vértice w distinto de r. Se chamarmos de franja o conjunto de todos os arcos vw tais que dist[v] < ∞ e dist[w] = ∞, o processo iterativo pode ser apresentado assim:
| enquanto a franja não estiver vazia, |
| .oo seja vw um arco da franja que minimiza dist[v] |
| .oo e faça dist[w] := dist[v] + 1. |
No fim de cada iteração, dist[w] deixa de ser ∞ e portanto a franja se altera. Quando a franja fica vazia, o processo iterativo termina e dist é o vetor das distâncias a partir de r.
Na verdade, não é necessário procurar explicitamente um arco vw que minimize dist[v]. Basta visitar os vértices numa ordem apropriada: primeiro r, depois os vizinhos de r, depois os vizinhos dos vizinhos de r, depois os vizinhos dos vizinhos dos vizinhos, e assim por diante. Essa estratégia é conhecida como busca em largura (= breadth-first search = BFS).
O algoritmo abaixo põe em prática as ideias da seção anterior. Para que os vértices sejam visitados na ordem certa, eles são mantidos numa fila.
O código abaixo resolve o problema das distâncias num digrafo G representado por um vetor Adj de listas de adjacência.
| Distâncias (G, r) ▷ busca em largura |
| 11 . para cada v em V(G) |
| 12 .ooo dist[v] := ∞ |
| 13 . dist[r] := 0 |
| 14 . Nova-Fila (r) |
| 15 . enquanto a fila não estiver vazia |
| 16 .ooo v := Sai-da-Fila ( ) |
| 17 .ooo para cada w em Adj[v] |
| 18 .oooooo se dist[w] = ∞ ▷ w descoberto |
| 19 .ooooooooo dist[w] := dist[v] + 1 |
| 10 .ooooooooo Entra-na-Fila (w) |
| 11 . devolva dist |
O comando Nova-Fila (r) cria uma fila com um só elemento igual a r. O comando Sai-da-Fila ( ) retira o primeiro (ou seja, o mais antigo) elemento da fila. O comando Entra-na-Fila (w) insere w no fim da fila.
Como os vértices são visitados na ordem imposta pela fila, temos as seguintes propriedades no início de cada execução do bloco de linhas 6-10:
Segue daí que, quando a execução do algoritmo termina, dist[s] é a distância de r a s para todo s.
Para mostrar que os invariantes i e ii de fato valem no início de cada iteração é preciso fazer a seguinte observação auxiliar sobre a estrutura da fila. Digamos que q1 é o primeiro elemento da fila, q2 o segundo, etc., e qk é o último. Então, se denotarmos dist[q1] por d, teremos
Exemplo B. Aplique o algoritmo Distâncias, com r = 3, ao digrafo definido pelas seguintes listas de adjacência:
| v | Adj[v] |
| 1 | (6) |
| 2 | (3, 6) |
| 3 | (2, 4, 6) |
| 4 | (1, 5) |
| 5 | (4, 6) |
| 6 | (1, 4) |
Veja o estado da fila e o estado do vetor dist
no início de cada iteração
(ou seja, imediatamente antes de cada execução da linha 6),
com -
indicando ∞
:
|
|
Exemplo C.
Aplique o algoritmo Distâncias
a partir do vértice 0
ao digrafo da figura.
Suponha que os vértices estão em ordem crescente de nomes
em cada lista de adjacência.
Eis o estado da fila e o estado do vetor dist
no início de cada iteração
(ou seja, imediatamente antes de cada execução da linha 6),
com -
indicando ∞
:
|
|
Quanto tempo o algoritmo Distâncias consome no pior caso? Vamos medir esse tempo em relação ao tamanho do digrafo, ou seja, em relação ao número n de vértices e ao número m de arcos do digrafo. No que segue, vamos supor que cada execução das funções que manipula a fila de vértices (linhas 4, 6 e 10) consome tempo constante, ou seja, uma quantidade de tempo que não depende de n nem de m.
Comecemos pelo consumo de tempo das linhas 5-10. O bloco de linhas 6-10, é executado no máximo n vezes, pois cada iteração retira um vértice da fila e cada vértice entra na fila no máximo uma vez. Para cada uma das n repetições do bloco de linhas 6-10, o bloco de linhas 8-10 é executado no máximo n−1 vezes, pois cada vértice tem no máximo n−1 vizinhos. Assim, o consumo de tempo do bloco de linhas 6-10 é limitado por n × (n−1). Concluímos que o bloco de linhas 5-10 consome Ο(n²) unidades de tempo. Mas essa cota superior é um tanto grosseira.
Para fazer uma estimativa mais fina, examinemos mais uma vez o bloco de linhas 6-10. Cada execução desse bloco processa um vértice v retirado da fila. Digamos que T(v) é o tempo que o bloco de linhas gasta para processar o vértice v. Cada execução do bloco processa um vértice diferente, donde o tempo total gasto para processar todos os vértices não passa de T(1) + T(2) + ⋯ + T(n). O tempo T(v) é proporcional ao comprimento da lista Adj[v], que é igual ao grau de saída g(v) do vértice v. Portanto, o tempo total gasto pelo bloco de linhas 6-10 é proporcional à soma g(1) + g(2) + ⋯ + g(n). Essa soma é igual ao número m de arcos do digrafo, e portanto o bloco de linhas 6-10 consome Ο(m) unidades de tempo. Mas isso merece uma correção. Para ser mais exato, o tempo T(v) é proporcional a 1 + g(v), onde o termo 1 corresponde ao consumo de uma execução da linha 6. Com essa correção, o bloco de linhas 6-10 consome Ο(n + m) unidades de tempo. Concluímos assim que o bloco de linhas 5-10 consome Ο(n + m) unidades de tempo.
Só falta levar em conta o tempo Ο(n) gasto com as operações de inicialização nas linhas 1-4. Feito isso, o algoritmo Distâncias consome
unidades de tempo. Como n + m é uma medida do tamanho do digrafo, podemos dizer que o algoritmo é linear.
Cada vez que um novo vértice w é descoberto durante a busca em largura — veja a linha 8 do algoritmo Distâncias — convém anotar o vértice v a partir do qual w foi descoberto. Para isso, basta fazer pai[w] := v, construindo assim um vetor pai de vértices indexado pelos vértices. Diremos que esse é um vetor de pais (= parent array = array of predecessors) da busca.
| 1Distâncias (G, r) |
| 11 . para cada v em V(G) |
| 12 .ooo dist[v] := ∞ |
| 13 . dist[r] := 0 |
| 14 . pai[r] := r |
| 15 . Nova-Fila (r) |
| 16 . enquanto a fila não estiver vazia |
| 17 .ooo v := Sai-da-Fila ( ) |
| 18 .ooo para cada w em Adj[v] |
| 19 .oooooo se dist[w] = ∞ |
| 10 .ooooooooo dist[w] := dist[v] + 1 |
| 11 .ooooooooo pai[w] := v |
| 12 .ooooooooo Entra-na-Fila (w) |
| 13 . devolva dist e pai |
O subdigrafo de G formado por todos os arcos vw tais que v = pai[w] é uma floresta radicada. Mais precisamente, é uma árvore radicada, já que r é a única raiz. Diremos que essa é a árvore da busca em largura (ou árvore de caminhos mínimos). Note que a árvore contém todos os vértices que estão ao alcance de r em G e só esses.
Ao final da execução do algoritmo, se dist[s] = ∞ então não existe caminho algum de r a s. Senão, a sequência
s, pai[s], pai[pai[s]], … , r
é o inverso de um caminho de r a s em G que tem comprimento dist[v]. Esse caminho é mínimo no seguinte sentido: nenhum outro caminho de r a v tem comprimento menor que dist[v].
Exemplo D. Aplique o algoritmo Distâncias com r = 0 ao digrafo do exemplo C. No fim da execução do algoritmo, o vetor pai estará no seguinte estado:
| v] | 0 | 1 | 2 | 3 | 4 | 5 |
| pai[v] | 0 | 5 | 0 | 0 | 0 | 3 |
Exemplo E. Considere novamente o digrafo do exemplo B. O algoritmo Distâncias, com r = 3, produz a árvore da busca em largura representada pelo seguinte vetor de pais:
| v] | 3 | 2 | 4 | 6 | 1 | 5 |
| pai[v] | 3 | 3 | 3 | 3 | 4 | 4 |
Nesta tabela, os vértices estão listados na ordem em que foram descobertos. A tabela pode ser reescrita colocando a primeira linha em ordem crescente:
| v] | 1 | 2 | 3 | 4 | 5 | 6 |
| pai[v] | 4 | 3 | 3 | 3 | 4 | 3 |
Faça um desenho da árvore de busca em largura demodo que a ordem da-esquerda-para-a-direita dos filhos de cada vértice corresponda à ordem em que os vértices foram descobertos.
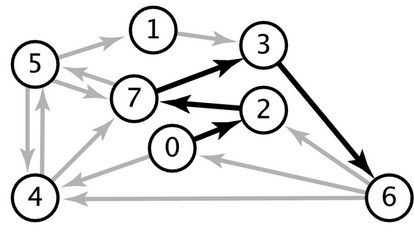
Exemplo F. O digrafo da figura tem vértices 0, 1, … , 7. Aplique o algoritmo Distâncias ao digrafo. Se começar pelo vértice 2, o algoritmo poduzirá a árvore de busca em largura indicada na figura.
| v] | a | b | c | d | e | f | g |
| p[v] | c | c | c | d | a | d | a |