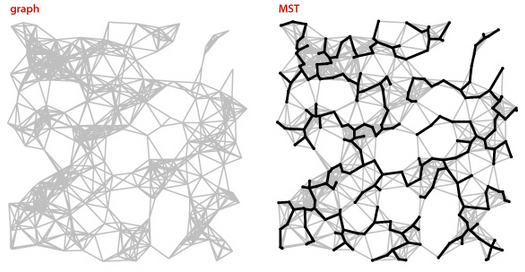
Esta página trata do problema das árvores geradoras de peso mínimo em grafos. Trata-se de uma generalização do problema da árvore geradora discutido no capítulo Árvores geradoras de grafos. O problema desta página é conhecido pelas iniciais MST de minimum spanning tree. A página trata, em particular, do célebre algoritmo de Prim para o problema da MST.
Esta página é inspirada no capítulo 23 de CLRS.
Suponha que cada aresta vw de um grafo tem um peso (= weight) numérico f(vw), que pode ser positivo, negativo, ou nulo. Diremos que f é uma função-peso definida sobre os arestas do grafo. O peso de um subgrafo T do grafo é a soma dos pesos das arestas de T e será denotado por f(T).
Uma MST (= minimum spanning tree) de um grafo com função-peso f é uma árvore geradora T do grafo que minimiza f(T). Considere o seguinte
Problema da MST: Dado um grafo G com função-peso f nas arestas, encontrar uma MST de G.
Uma instância do problema da MST tem solução se e somente se G é conexo. Por isso, vamos nos restringir desde já a grafos conexos.
Exemplo A. Cada linha representa uma aresta do grafo. O peso de cada aresta é proporcional ao comprimento geométrico do segmento de reta que representa a aresta na figura.
| vw) | 4 5 | 4 7 | 5 7 | 0 7 | 1 5 | 0 4 | 2 3 | 1 7 | 0 2 | 1 2 | 1 3 | 2 7 | 6 2 | 3 6 | 6 0 | 6 4 |
| f(vw) | 35 | 37 | 28 | 16 | 32 | 38 | 17 | 19 | 26 | 36 | 29 | 34 | 40 | 52 | 58 | 93 |
O conjunto de arestas 0 7 7 1 7 5 5 4 0 2 2 3 2 6 define uma árvore geradora do grafo. O peso dessa árvore é 35 + 28 + 16 + 17 + 19 + 26 + 40 = 181. Nenhuma outra árvore geradora tem peso menor, embora isso não seja óbvio.
Seja a1, a2, … , am a sequência das arestas doi grafo em ordem crescente de pesos. No início da primeira iteração, pinte um vértice qualquer de preto e os demais vértices de branco. Para i = 1, 2, … , m faça o seguinte: se uma ponta de ai é preta e outra é branca, acrescente ai à árvore e pinte de preto a ponta que era branca.
O célebre algoritmo de Prim, descoberto por R. C. Prim em 1957, resolve o problema da MST de maneira eficiente. (E. W. Dijkstra também descobriu o algoritmo.)
Nossa primeira descrição do algoritmo de Prim será feita num nível de abstração bastante alto. O algoritmo é iterativo. Cada iteração começa com uma subárvore T de G. Na primeira iteração, T tem um único vértice e nenhuma aresta. Imagine que os vértices de T são pretos e todos os demais são brancos. Diremos que a franja de T é o conjunto de todas as arestas de G que têm uma ponta preta e outra branca. O processo iterativo pode então ser descrito assim:
| enquanto a franja não estiver vazia, |
| .oo escolha um aresta da franja que tenha peso mínimo, |
| .oo seja vw a aresta escolhida, |
| .oo troque T por T + vw. |
No fim de cada iteração, a ponta de vw que era branca fica preta e portanto a franja se altera. Quando a franja ficar vazia, T é uma árvore geradora de peso mínimo, a menos que G não seja conexo.
O algoritmo tem caráter guloso, pois escolhe o aresta vw com base em considerações locais, sem qualquer preocupação com o objetivo global de obter uma árvore de peso mínimo.
O algoritmo está correto. Suponha que G é conexo, pois do contrário a instância do problema não tem solução. Nesse caso, é claro que o algoritmo produz uma árvore geradora. Resta mostrar que essa árvore é ótima, ou seja, tem peso mínimo. Para isso, basta provar que, no início de cada iteração,
| T é subgrafo de alguma MST de G. | (*) |
Eis um esboço da prova. Suponha que no início de uma certa iteração T é subgrafo de uma MST M. Durante esta iteração, uma aresta vw será acrescentada a T. Se essa aresta já está em M então T + vw é subgrafo de M, como queríamos provar.
Suponha agora que vw não está em M. A árvore M tem um único caminho, digamos C, de v a w. Algum aresta xy de C está na franja de T e portanto f(xy) ≥ f(vw). Observe que
é uma árvore geradora. O peso dessa nova árvore não é maior que o peso de M. Concluímos que a nova árvore geradora é tão ótima quanto M. Finalmente, observe que T + vw é subgrafo de M + vw − xy. Assim, no início da próxima iteração, T é subgrafo de uma MST, como queríamos provar.
Seja (W1, W2)
uma bipartição do conjunto de vértices tal que ⎮W1⎮−⎮W2⎮
vale −1, 0 ou 1.
Seja T1 uma
árvore geradora de peso mínimo
no grafo
induzido por W1.
Seja xy
um aresta de peso mínimo dentre as que têm uma ponta em
W1 e outra em W2.
Seja T2 uma
árvore geradora de peso mínimo
no grafo induzido por W2.
Devolva T1 + xy + T2.
Esse algoritmo está correto?
Tal como descrito na seção anterior, o algoritmo de Prim é ineficiente, uma vez que recalcula a franja de T a cada iteração (mesmo que ela tenha mudado muito pouco em relação à iteração anterior). Para que o algoritmo seja mais rápido, é preciso inventar uma representação eficiente da franja. É o que faremos a seguir.
No início de cada iteração, temos um conjunto Q de vértices e um vetor chave que associa um número a cada vértice do grafo. (O complemento de Q é o conjunto de vértices da subárvore T que está em construção.)
No início de cada iteração, a franja é o conjunto de todas as arestas que têm uma ponta no complemento de Q e outra em Q. Para cada vértice w de Q, o número chave[w] é o peso da aresta mais leve dentre todas as arestas da franja que têm ponta w. O processo iterativo pode ser descrito assim:
| enquanto Q não estiver vazio, |
| .oo escolha q em Q que minimize chave[q], |
| .oo remova q de Q, |
| .oo para cada aresta da forma qw, |
| .ooooo se chave[w] > f(qw), |
| .oooooooo faça chave[w] := f(qw). |
Para reescrever o algoritmo de maneira mais formal e detalhada, vamos supor que o grafo G é conexo e representado por um vetor Adj de listas de adjacência. O conjunto Q será organizado como uma fila-com-prioridades. A árvore T será representada por um vetor de pais como o da página Distâncias e busca em largura.
| Prim (G, f ) |
| 11 . V := V(G) |
| 12 . para cada w em V |
| 13 .ooo chave[w] := ∞ |
| 14 . escolha qualquer r em V |
| 15 . chave[r] := 0 |
| 16 . Q := Nova-Fila-com-Prioridades ( ) |
| 17 . para cada w em V |
| 18 .ooo Insere-na-Fila (w, Q) |
| 19 . enquanto Q não está vazia |
| 10 .ooo q := Extraia-Min (Q) |
| 11 .ooo para cada w em Adj[q] |
| 12 .oooooo se w ∈ Q e f(qw) < chave[w] |
| 13 .ooooooooo Diminua-Chave (w, Q, f(qw)) |
| 14 .ooooooooo pai[w] := q |
| 15 . B := { vw : v = pai[w], w ∈ V, w ≠ r } |
| 16 . devolva (V, B) |
Algumas observações que ajudam a entender o código:
Desempenho. O consumo de tempo do algoritmo Prim depende da implementação da fila-com-prioridades Q. Uma análise análoga à que fizemos no caso do algoritmo Dijkstra mostra que
Note que o algoritmo Prim é assintoticamente mais rápido com a fila simples que com a fila sofisticada se nos restingirmos a grafos densos. (No caso da fila simples, nem é necessário construir a fila explícitamente: basta examinar todos os vértices de Q em cada iteração.)
-representando
∞. Tome r = 2.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | - | 3 | - | 4 | 5 | - | - | - | - |
| 2 | 3 | - | 9 | - | 6 | - | - | - | - |
| 3 | - | 9 | - | - | 8 | 2 | - | - | - |
| 4 | 4 | - | - | - | 6 | - | 6 | 7 | - |
| 5 | 5 | 6 | 8 | 6 | - | 9 | - | 8 | - |
| 6 | - | - | 2 | - | 9 | - | - | - | - |
| 7 | - | - | - | 6 | - | - | - | 8 | - |
| 8 | - | - | - | 7 | 8 | - | 8 | - | - |
| 9 | - | - | - | - | - | - | - | - | - |
A chain is only as strong as its weakest link.