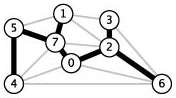
Esta página introduz o conceito de árvore geradora de um grafo e mostra como calcular uma árvore geradora.
Uma subárvore de um grafo G
é qualquer árvore que seja subgrafo de G.
Estamos particularmente interessados em subárvores que cobrem
o grafo todo,
conforme a seguinte definição.
Uma árvore geradora
(= spanning tree)
de um grafo G
é qualquer árvore que seja um
subgrafo gerador de G.
(Teria sido mais consistente dizer
subárvore geradora
,
mas a tradição manda eliminar o sub
.)
Se um grafo G tem uma árvore geradora então G é conexo. A recíproca não é tão óbvia, o que leva ao seguinte
Problema da árvore geradora: Dado um grafo G, encontrar uma árvore geradora de G.
A solução do problema (veja a seção seguinte) é simples, mas ensina algumas lições úteis.
Nosso algoritmo para o problema da árvore geradora terá o seguinte comportamento: recebe um grafo e devolve uma árvore geradora de G ou informa que G não é conexo. No segundo caso, fica óbvio que essa instância do problema não tem solução.
O algoritmo é iterativo. Cada iteração começa com uma subárvore T (não necessariamente geradora) de G. No começo da primeira iteração, T tem um só vértice e nenhuma aresta. Diremos que a franja de T é o conjunto de todas as arestas de G que têm uma ponta em T e outra fora de T. O processo iterativo pode então ser descrito assim:
| enquanto a franja não estiver vazia, |
| .oo tome uma aresta vw da franja e |
| .oo troque T por T + vw. |
Ao fim de cada iteração, T ganha um novo vértice e uma nova aresta e portanto a franja de T se altera. Na última iteração, a franja fica vazia e o processo iterativo termina. Nesse momento, o conjunto V(T) é igual ao conjunto de vértices de G ou é isolado. No primeiro caso, T é uma árvore geradora de G. No segundo, V(T) é evidência de que G não é conexo e portanto não tem árvore geradora.
certificadoo seu algoritmo devolve para provar uma resposta afirmativa? Que
certificadodevolve para provar uma resposta negativa? (Sugestão: Use o algoritmo da árvore geradora.)