Grafos não-dirigidos

Um grafo é simétrico se para cada arco da forma vw existe um arco da forma wv, ou seja, se cada arco faz parte de um ciclo de comprimento dois.

Um grafo não-dirigido é um grafo simétrico em que os arcos estão geminados: cada arco a tem um gêmeo b tal que

Se dois arcos, a e c, são ambos da forma vw então seus gêmeos, digamos b e d, têm a forma wv e são distintos.

Uma aresta (= edge) de um grafo não-dirigido é um par ab de arcos gêmeos. Diremos que os arcos a e b são as duas metades da aresta ab. Se a ponta inicial e a final de a coincidem, diremos que a aresta ab é um laço.

Você pode imaginar que uma aresta é uma grande rodovia (como a rodovia dos Bandeirantes ou a Anhanguera, que ligam São Paulo a Campinas): um dos arcos que formam a aresta é a pista que vai e outro arco é a pista que vem.

Representação SGB de grafos não-dirigidos

Na estrutura de dados do SGB, arestas são representadas da seguinte maneira. Os dois arcos que constituem uma aresta são alocados em posições consecutivas da memória. Assim, se ab é uma aresta então a e b são objetos Arc* tais que

Mais precisamente: se a é da forma vw, sendo v e w objetos Vertex* distintos, então

Se v ≡ w (e portanto ab é um laço) então os arcos a e b estão ambos na lista de arcos que saem de v e b ≡ a+1 ≡ anext.

(Eu acho que o SGB poderia ter usado um esquema mais simples: um ponteiro que leve cada arco no seu gêmeo. Mas quem sou eu para discutir com Knuth!)

Muitas das funções do SGB permitem gerar grafos não-dirigidos. Por exemplo, no módulo GB_RAND do SGB, o grafo

é não-dirigido (quinto argumento igual a 0), sem laços (terceiro argumento igual a 0), mas possivelmente dotado de arestas paralelas (quarto argumento igual a 1). O primeiro argumento, n, é o número de vértices. O segundo, m, é o número de arestas, ou seja, a metade do número de arcos. (Se o quinto argumento fosse diferente de 0, m seria o número de arcos.)

Exercícios 1

Escreva uma função C que receba um grafo g e devolva 1 se o grafo for não-dirigido e 0 em caso contrário.
Melhore a função do exercício anterior de modo que ela também verifique se blen ≡ alen sempre que a e b forem arcos gêmeos.
Duas arestas são paralelas se têm o mesmo par de pontas. Suponha que um dado grafo não-dirigido não tem arestas paralelas nem laços. Se o grafo tem n vértices, quantas arestas pode ter?

Matrizes e desenhos

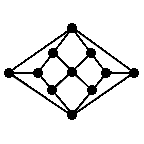
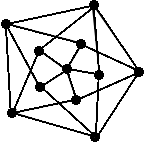
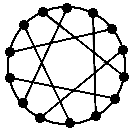
Grafos não-dirigidos podem ser representados por matrizes de adjacência, como já fizemos com grafos em geral. Grafos pequenos também podem ser representados por figuras. Veja alguns exemplos particularmente redondos e simétricos que copiei da web:

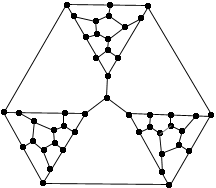
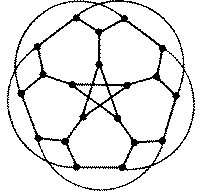
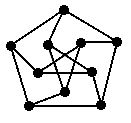
A última figura mostra o célebre grafo de Petersen. Para o SGB, ele é disjoint_subsets (5, 2). A função disjoint_subsets está definida no bloco 36 do módulo GB_BASIC.

Exercícios 2

Faça uma fugura do grafo complete (6) do SGB. A macro complete está definida no bloco 6, p.123, do módulo GB_BASIC do SGB. (Para qualquer n, o grafo complete (n) é o mesmo que board (n, 0, 0, 0, −1, 0, 0). Você sabe o que faz a função board?) Fora do SGB, esse grafo é conhecido como K₆.
Faça uma figura do grafo circuit (7) do SGB. A macro circuit está definida no bloco 6, p.123, do módulo GB_BASIC do SGB. (Para qualquer n, o grafo circuit (n) é o mesmo que board (n, 0, 0, 0, 1, 1, 0).)
Faça figuras (com lapis e papel) dos seguinte grafos:
miles (10, 0, 0, 1, 0, 4, 0)
games (9, 0, 0, 0, 0, 0, 0, 0),
subsets (2, 1, −3, 0, 0, 0, 1, 0)
subsets (2, 1, −4, 0, 0, 0, 1, 0)
board (5, 4, 0, 0, −1, 0, 0)
board (5, 4, 0, 0, −1, 1, 0)
(Sugestão: use uma adaptação do tarefa de programação A para ver os grafos.

Adjacência

Dois vértices, v e w, em um grafo não-dirigido são adjacentes (ou vizinhos) se existe uma aresta com pontas v e w. Ao contrário do que acontece com grafos em geral, a relação de adjacência em grafos não-dirigido é simétrica: v é adjacente a w se e só se w é adjacente a v.

A reflexividade da relação de adjacência é uma questão sem importância. Você pode dizer que todo vértice é adjacente a si mesmo ou pode dizer que v é adjacente a si mesmo somente se o grafo possui algum arco da forma vv. Tanto faz.

Grau de um vértice e grau de um conjunto de vértices

Num grafo não-dirigido, o grau de um vértice v é o número de arestas que têm ponta v, sendo os laços contados em dobro. O grau de v será denotado por g(v). É evidente que

para todo vértice v. (Lembrete: ge(v) é o grau de entrada e gs(v) o grau de saída de v.)

O grau de um conjunto de vértices, digamos X, é o número de arestas que têm uma ponta em X e a outra ponta fora de X. É evidente que g(X) ≡ ge(X) ≡ gs(X).

Conexão e componentes

Num grafo não-dirigido, se existe um caminho de um vértice v a um vértice w então também existe um caminho de w para v. Em virtude dessa observação, se dois vértices x e y de um grafo não-dirigido estão ambos no território de um terceiro vértice então existe um caminho x a y.

Outra consequência: se T é o território de algum vértice em um grafo não-dirigido então o grau de T é nulo. Assim, o território de um vértice v se confunde com o componente que contém v.

Todo grafo não-dirigido com um só componente é fortemente conexo. A propósito, quando se trata de grafos não-dirigido, a expressão fortemente conexo é normalmente abreviada para conexo.

Exercícios 3

Seja v um vértice de um grafo não-dirigido e suponha que o território de v contém todos os vértices do grafo. Prove que o grafo é (fortemente) conexo. Mostre que esta propriedade não vale para grafos em geral.
Escreva uma função C que receba um grafo não-dirigido e devolva 1 se o grafo é conexo e 0 em caso contrário.
Seja G um grafo não-dirigido. Mostre que G é conexo se e somentte se G tem um único componente.

Ciclos e circuitos

Ciclos em grafos não-dirigidos têm uma propriedade óbvia mas importante: se (v₀, a₁, v₁, a₂, v₂, … , a_k, v_k) é um ciclo então o seu inverso (v_k, b_k, … , v₂, b₂, v₁, b₁, v₀) também é um ciclo, sendo b_j o arco gêmeo de a_j.

Grafos não-dirigidos estão repletos de ciclos da forma (v, a, v) e ciclos da forma (v, a, w, b, v), onde b é o gêmeo de a. Esses ciclos são considerados degenerados; todos os demais ciclos são não-degenerados. Ciclos não-degenerados num grafo não-dirigido são conhecidos como circuitos. Note que a definição não exclui circuitos curtos: um grafo pode ter circuitos de comprimento 1 ou 2.

Exercícios 4

Escreva uma função que encontre um circuito num grafo não-dirigido dado (ou decida que o grafo não tem circuitos).

Árvores

Uma árvore é um grafo não-dirigido conexo sem circuitos. Toda árvore com n vértices tem exatamente n−1 arestas (ou seja, n−1 pares de arcos gêmeos).

Uma propriedade importante: se um grafo G é uma árvore então, para todo par (v, w) de seus vértices, existe um e apenas um caminho de v a w. A recíproca é verdadeira: se para todo par (v, w) de vértices de um grafo G existe um e apenas um caminho de v a w, então G é uma árvore.

Cuidado! As expressões o vértice v é filho do vértice w e o vértice w é pai do vértice v não fazem sentido. (As expressões só começam a fazer sentido se um dos vértices da árvore for escolhido como raiz.)

Eis um conceito que pode ser útil, apesar do nome engraçado. Uma caminhárvore num grafo é uma sequência (v₀, a₁, v₁, a₂, v₂, … , a_n, v_n) em que v₀, v₁, v₂, … , v_n são vértices distintos dois a dois e cada a_k é um arco que vai

Exercícios 5

Escreva uma função em C que decida se um grafo dado é ou não uma árvore.
Mostre que todo grafo conexo tem uma caminhárvore que contém todos os seus vértices. (Uma caminhárvore desse tipo é conhecida como árvore geradora do grafo.)
Mostre que toda árvore tem uma caminhárvore que contém todos os seus vértices e arestas.
Suponha que um grafo G tem uma caminhárvore que contém todos os seus vértices e arestas. Mostre que G é uma árvore.
Seja G um grafo não-dirigido conexo com n vértices e n−1 arestas. Mostre que G é uma árvore.
Seja G um grafo não-dirigido sem circuitos com n vértices e n−1 arestas. Mostre que G é uma árvore.