Um grafo (= graph) é um animal formado por dois conjuntos: um conjunto de coisas chamadas vértices e um conjunto de coisas chamadas arcos; cada arco está associado a dois vértices: o primeiro é a ponta inicial do arco e o segundo é a ponta final. Você pode imaginar que um grafo é um mapa rodoviário idealizado: os vértices são cidades e os arcos são estradas de mão única.
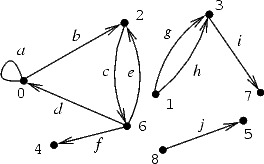
Exemplo 1: Digamos que os vértices de nosso grafo são 0, 1, 2, 3, 4, 5, 6, 7, 8 e os arcos são a, b, c, d, e, f, g, h, i, j. Então a seguinte tabela define um grafo:
ponta inicial 0 0 2 6 6 6 1 1 3 8 arco a b c d e f g h i j ponta final 0 2 6 0 2 4 3 3 7 5 
Se um arco a
tem ponta inicial v e ponta final w,
dizemos que a
vai de v a w.
Dizemos também que
a sai de v
e entra em w.
Às vezes, um arco com ponta inicial v
e ponta final w
será denotado por (v, w) ou por
v→w
ou simplesmente por vw.
Os arcos são dirigidos
;
há quem goste de enfatizar esse fato dizendo que o grafo
é dirigido (= directed).
De maneira mais formal,
podemos dizer que um grafo é um terno (V, A, f ),
onde V e A
são conjuntos finitos arbitrários
e f é a função que associa a cada
elemento de A
um par ordenado de elementos de V.
Às vezes, a função f é subentendida
e dizemos
simplesmente o grafo (V, A)
.
Se o grafo como um todo é denotado por
G,
o seu conjunto de vértices será denotado por
VG
e o seu conjunto de arcos por AG.
Se o grafo for denotado por
g,
os conjuntos de vértices e arcos serão denotados por
Vg e Ag respectivamente.
Um arco é um laço (= loop = self-loop) se sua ponta inicial coincide com sua ponta final, ou seja, se o arco é da forma (v, v). Dois arcos são paralelos se têm a mesma ponta inicial e a mesma ponta final, ou seja, se os dois arcos são da forma (v, w). Dois arcos são antiparalelos se a ponta inicial de um é ponta final do outro, ou seja, se um arco é da forma (v, w) enquanto o outro é da forma (w, v).
Um grafo é simétrico (= symmetric) se para cada arco da forma (v, w) existe um arco da forma (w, v). Um tipo especial muito importante de grafo simétrico é o grafo não-dirigido (= undirected); vamos tratar desse tipo de grafo mais tarde.
A natureza está cheia de grafos. Eis alguns exemplos:
dependência: um arquivo v é construído a partir de todos os arquivos w para os quais existe um arco (v, w). Exemplo: se os arquivos são aaa.y, aaa.c, bbb.c, bbb.h, aaa.o, bbb.o, aaa e bbb, poderemos ter arcos da forma (aaa, aaa.o), (aaa.o, aaa.c), (aaa.o, bbb.h), etc. O utilitário make do Linux trabalha sobre grafos deste tipo.
girafa,
girava,
cavalo, etc.). Há um arco de x a y se e só se as duas palavras diferem em exatamente uma posição (por exemplo, há um arco de
girafapara
girava). É claro que o grafo não tem laços nem arcos paralelos, mas é simétrico. (Poderíamos eliminar a simetria apagando o arco de x a y se y precede x no dicionário.)
girafae chegar em
cavaloandando pelo arcos do grafo?
Um vértice w é adjacente a (ou vizinho de) um vértice v se existe um arco da forma (v, w), ou seja, se existe um arco com ponta inicial v e ponta final w. A relação de adjacência entre vértices não é simétrica: w pode ser adjacente a v sem que v seja adjacente a w.
Exemplo 2: No exemplo 1, os vértices adjacentes a 6 são 0, 2 e 4. O único vértice adjacente a 8 é 5.
A matriz de adjacências, digamos M, de um grafo tem linhas e colunas indexadas pelos vértices. Para cada par (v, w) de vértices, M[v, w] é o número de arcos com ponta inicial v e ponta final w. (Algumas pessoas preferem uma matriz booleana: M[v, w] vale 1 se existe algum arco de v a w e vale 0 em caso contrário.)
Exemplo 3: Eis a matriz de adjacências do grafo do exemplo 1 (os
0foram trocados por-para tornar a figura mais legível):
0 1 2 3 4 5 6 7 8 0 1 - 1 - - - - - - 1 - - - 2 - - - - - 2 - - - - - - 1 - - 3 - - - - - - - 1 - 4 - - - - - - - - - 5 - - - - - - - - - 6 1 - 1 - 1 - - - - 7 - - - - - - - - - 8 - - - - - 1 - - -
A matriz de adjacências de um grafo pode ser um bom substituto para um desenho do grafo, especialmente se os vértices forem colocados em uma ordem apropriada. Por exemplo, a segunda das matrizes abaixo revela melhor a estrutura do grafo que a primeira, embora ambas representem o mesmo grafo.
|
|