
|
|
|
CapVIII-pg1 |
|
Até agora falamos sobre quatro invariantes (sob homeomorfismos) de superfícies: dois invariantes binários (ser ou não ser simplesmente conexa, ter ou não ter a propriedade de Jordan) e dois numéricos (o número de componentes de bordo, a característica de Euler). |
Invariante é o nome que se dá a qualquer propriedade das superfícies que não se altera sob homeomorfismos. Em outras palavras, se duas superfícies são homeomorfas, quer dizer, uma pode ser transformada na outra através de deformações e cortes com colagem (desde que a colagem se dê no mesmo lugar), então ambas têm a mesma propriedade. Se uma é simplesmente conexa a outra também é, se uma não tem a propriedade de Jordan a outra também não tem, a característica de Euler e o número de componentes de bordo são iguais nas duas, etc. |
Neste Capítulo trataremos de um quinto invariante, que é a orientabilidade da superfície. Esse invariante também é binário: uma superfície ou é ou não é orientável. |
Todos os exemplos exibidos até agora foram de superfícies orientáveis, à exceção da superfície azul na Página 1 do Capítulo III. Para discorrer sobre as superfícies não orientáveis, recorreremos a alguns exemplos. Vejamos então primeiro esses exemplos para depois fazermos um pouco de teoria. |
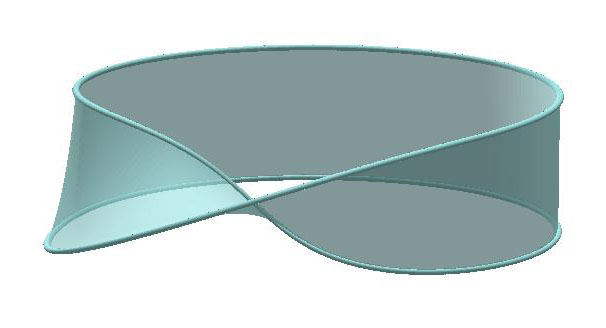
O primeiro é a Faixa de Moebius, mostrado de duas formas ligeiramente diferentes na figura abaixo, que são isotópicas entre si (tente imaginar você mesmo a isotopia!). |

|

|
A Faixa de Moebius pode ser fabricada facilmente com uma tira de papel. Faz-se uma torção na tira e então os extremos são colados. Se você fizer com papel, no entanto, não obterá um formato exatamente igual ao da figura abaixo, por causa das propriedades físicas do material. |
Os outros exemplos serão chamado de superfícies A, B e C, na falta de uma nomenclatura especial para elas. Elas também podem ser feitas em papel. |
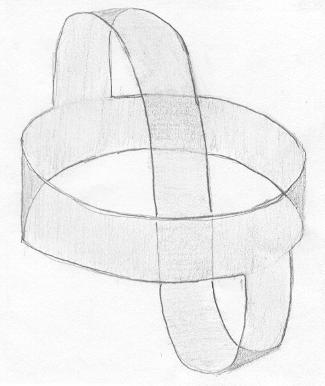
| Superfície A. |
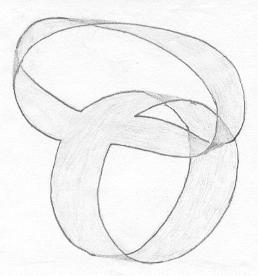
| Superfície B. |
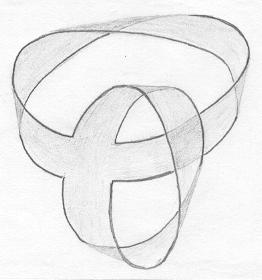
| Superfície C. |
Antes de definirmos orientabilidade, no entanto, façamos uma pequena análise dessas superfícies à luz dos quatro invariantes que já conhecemos. Isso pode nos ajudar a ganhar uma certa familiaridade com elas. |
Comecemos pelo número de componentes de bordo. A Faixa de Moebius tem apenas uma, e o mesmo vale para as superfícies A e B. A superfície C, por outro lado, tem duas componentes de bordo. Isso demonstra, em particular, que a superfície C não pode ser homeomorfa a nenhuma das outras três. |
E as outras, serão isotópicas entre si? |
|
CapVIII-pg1 |
|