|
|
CapVIII-pg2 |
|
De fato, as superfícies A e B são isotópicas. Para ver isso, procedemos em duas etapas. A primeira pode ser realizada em papel (não sem amassá-lo um pouco). Quanto à segunda etapa, veremos que o papel não se presta às deformações de que necessitaremos, embora possamos dar um jeito com uma pequena trapaça. |
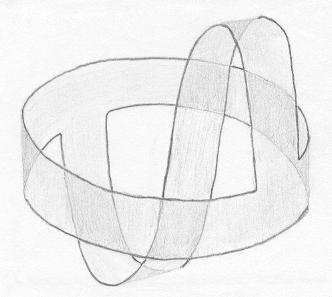
Primeira etapa. Começamos olhando para a superfície A, aqui vista de outro ângulo. Observe a faixa horizontal de formato cilíndrico, onde se apóia a tira ondulada do meio. |

|
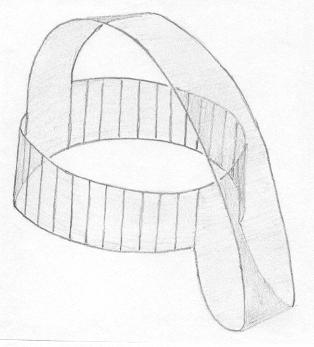
A faixa cilíndrica do meio é transformada num anel, empurrando-se o bordo de baixo para o centro e parte de cima para fora. |

|
Continuando esse processo, ficamos ao final com a faixa cilíndrica do "lado avesso". Com o papel, a deformação não será tão suave como indicado, mas ao final o resultado é o mesmo. Tente fazer! |

|
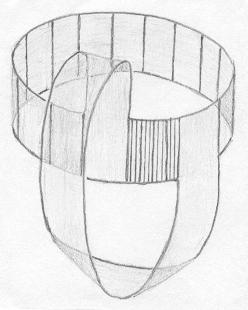
Segunda etapa. Agora fazemos uma deformação na faixa cilíndrica de modo a encolher um dos lados e esticar o outro. O tracejado no desenho indica isso: é como se fosse uma sanfona. |
|
|
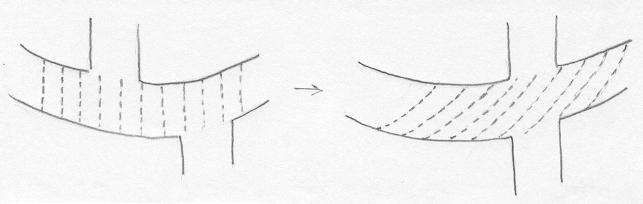
Depois alinhamos as extremidades da outra faixa, como indicado abaixo. |
|
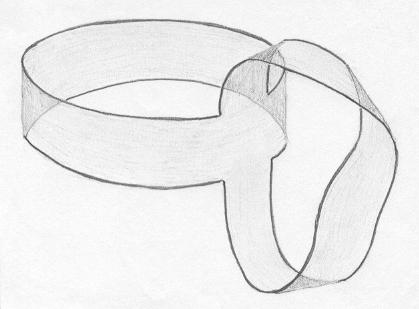
O resultado é exatamente o que queríamos: a superfície B. |
|
Observe que as duas deformações da segunda parte não podem ser feitas com papel. No entanto podemos trapacear, cortando a tira e arrastando-a por meia volta até obter o alinhamento, como no desenho acima. |
Agora que sabemos que as superfícies A e B são homeomorfas (até mais do que isso, são isotópicas), podemos nos referir só a uma delas, por exemplo, a superfície A. Tudo o que afirmarmos para a superfície A valerá automaticamente para a superfície B. |
|
CapVIII-pg2 |
|