| 
|
|
CapVIII-pg3 |
|
E quanto à conectividade simples? Algumas dessas superfícies é simplesmente conexa? |
A resposta é não! Nenhuma delas é simplesmente conexa! |
Para ver que isso é verdade, basta acharmos uma curva não retrátil na superfície. Vejamos por exemplo na Faixa de Moebius, o que seria uma curva retrátil e uma curva não retrátil. |

| 
|
O leitor está convidado a achar curvas não retráteis na superfície A e na superfície C! |
Deixaremos a discussão da propriedade de Jordan para mais adiante, depois de definirmos o conceito de orientabilidade. Antes disso, calculemos a característica de Euler de cada uma delas. Se as características de Euler da superfície A e da Faixa de Moebius forem diferentes, então poderemos concluir que essas superfícies não são homeomorfas. |
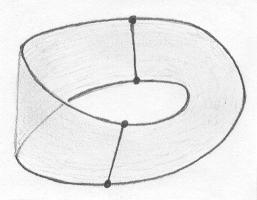
Na Faixa de Moebius, colocamos um grafo de duas faces (retangulares), como na figura abaixo. Temos F=2, A=6, V=4, logo X=0. |
|
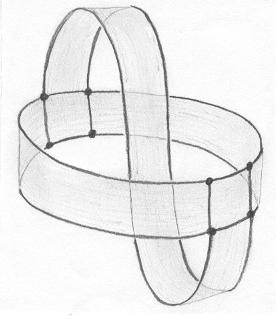
Já na superfície A, colocamos um grafo com F=5, A=14 e V=8, donde X = -1. |
|
Como as carcaterísticas de Euler são diferentes, concluímos que as duas superfícies não podem ser homeomorfas! |
Procure mostrar você mesmo que a superfície C tem característica de Euler igual a -1. Ou seja, as superfícies A e C têm a mesma característica de Euler, ambas não satisfazem à propriedade de Jordan (como veremos adiante), ambas não são simplesmente conexas e ambas não são orientáveis (também veremos adiante). O único invariante que as distingue, dos que foram apresentados aqui, é o número de componentes de bordo, igual a 1 para superfície A e igual a 2 para a superfície C. |
|
CapVIII-pg3 |
|